基于ansys的先张法张拉台座结构优化研究
董建伟, 段志东, 夏文传
(兰州交通大学 甘肃 兰州 730000)
0 概述
先张法是在混凝土浇筑前张拉预应力筋,将张拉的预应力筋临时锚固在张拉台座上,然后浇筑混凝土待其完全凝固,借助混凝土与预应力筋之间的黏结作用,对混凝土施加预应力的施工工艺。墩式台座[1]是利用拉杆和撑杆来保持平衡,但使用过程中稳定性较差,位移和倾斜现象较为明显,很难保证3个受力点始终相交于一点。压杆式台座应用范围最广,分为明压和暗压。明压占用场地较大,限制了台座的多用性,而暗压由于压柱的下埋,张拉力和压柱中心错开,台座需要克服偏心力矩作用,计算时边界条件和自重使得截面偏大,配筋增加。墩板式台座[2]是结合墩式台座和压柱式台座演变而来的,特点是采用变截面和加长墩长度来提高承端墩的抗倾覆能力[3],施工方便,结构简单,但是对于地基要求较高,需要有足够承载能力的地基条件。格鲁吉亚梁场位置靠近河道,地基条件较为薄弱,因此张拉台座考虑采用墩柱式台座,使用桩来代替拉杆和撑杆,其特点是利用桩来提高了台座的稳定性,而大尺寸墩身有效地抵消了台座板的受压,张拉荷载很大程度地被地基所吸收。进行这样的改造,台座结构形式简单,受力明确,但是过大墩身与桩也提高了造价,因而需要对台座的结构形式进行优化分析。
响应面法[4](RSM)是一种数学方法和统计方法结合的产物,用来将受多个变量影响的响应问题建模分析,从而得出最优响应值。基本思想是利用有限元的计算结果来拟合一个具有明确二次表达式的响应面来逼近真实的极限状态曲面[5],从而优化结构使其得到最优解的可靠度分析。
文中以格鲁吉亚施工项目为研究对象,先对于台座结构进行模拟分析,确定墩柱式台座满足项目要求,然后采用响应面法对台座设计参数进行拓扑优化[6],最后验算优化分析对于结构刚度的影响。
1 台座设计
1.1 台座形式
根据格鲁吉亚施工方案要求,设计采用7长线台座,设计长度为160.4 m,每线可同时张拉3片T梁,台座张拉控制力为199.32 kN。先张法墩柱式台座及配筋图如图1所示。
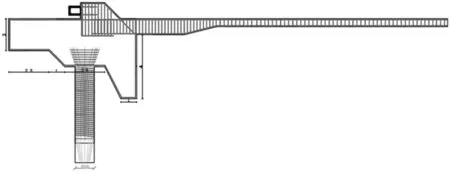
图1 墩柱式台座结构配筋图
1.2 混凝土本构关系
按混凝土规范[7]取值,εcu=0.0033 mm,ε0=0.002 mm。混凝土材料技术指标如表1。
混凝土应力应变表达式为
上升段
(1)

表1 混凝土材料技术指标
下降段
σc=fc(ε0<εc≤εcu)
(2)
得到混凝土应力应变关系曲线如图2所示。

图2 混凝土应力应变曲线
1.3 建模
结构有限元模型拟采用分离式建模[8],采用Solid65单元模拟混凝土台座,Link180单元模拟钢筋。由于结构的对称性,建立1/4模型。受力钢筋主筋均采用HRB400,泊松比为0.25,抗拉强度设计值为:fy=360 MPa。桩基摩擦力平均分配到桩表面节点,共计403个节点,模型划分实体单元数为31958个,钢筋单元数为4280个。得到有限元模型和钢筋布置图如图3所示。
经过有限元法计算结果如图4所示,牛腿最大主拉应力为1.85 MPa,最大拉应力发生在牛腿和台座板接触部位,小于C40混凝土的抗拉强度设计值1.89 MPa。桩最大主拉应力为1.3 MPa,发生在桩和扩大基础接触面,小于C30混凝土抗拉强度设计值1.43 MPa,均满足设计要求。

图3 有限元模型及钢筋分布图
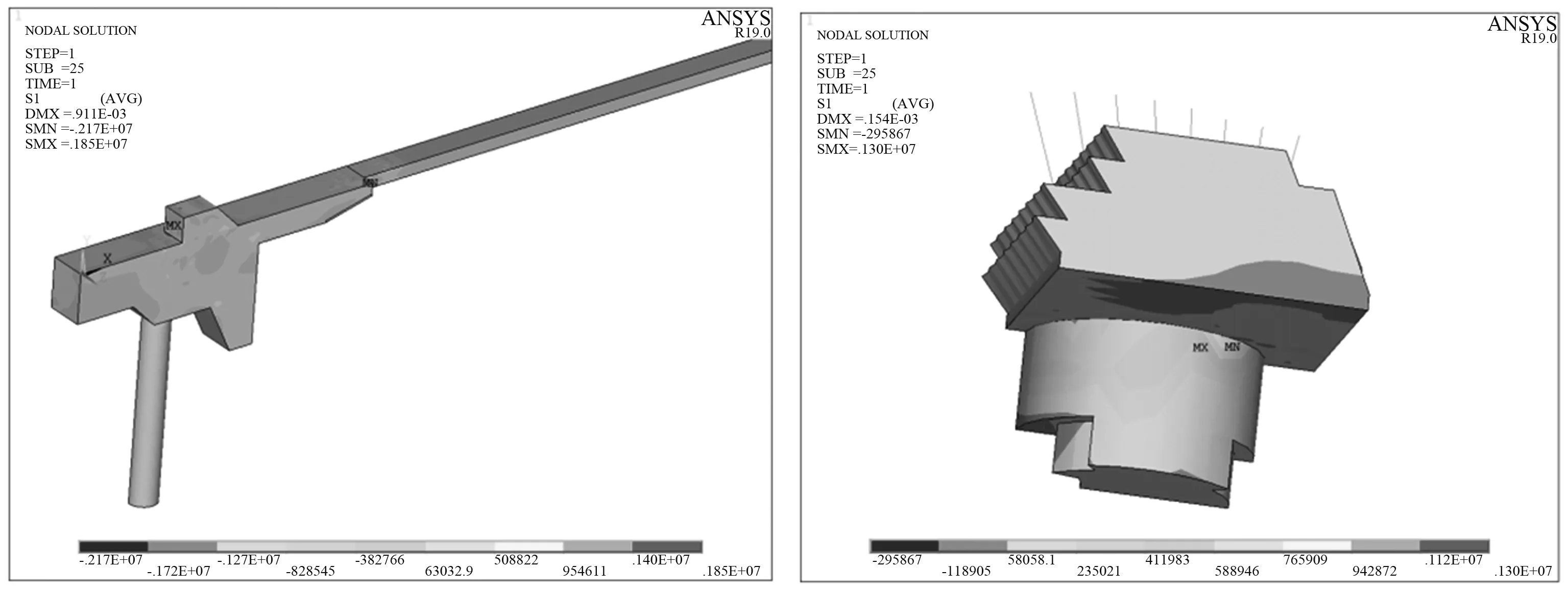
图4 关键部位最大主拉应力值
2 理论分析
响应面法是一种以实验条件来寻优的方法,用于解决非线性数据处理的相关问题,通过对过程的回归拟合[9]、响应曲面[10]分析和等高线的绘制来求出相应于各因素水平的响应值,最后基于响应值来找出预测结果的响应最优值。
实际工程中优化函数多采用全二阶多项式[11](Full 2nd-Order Polynomial)来逼近,一般形式为
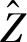
(3)
式中:n为自变量个数,β0,βi,βij为待定系数,γ为随机误差。
对结构参数进行m次(m>n+1)设置并分别进行数值计算,得到Z关于m个数值试验值,将这些参数和对应的响应面预测值代入(3)式,得到如下方程组

p=1,……,m
(4)
式(4)的矩阵形式为

(5)
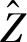
假设这m次试验的数值向量为
Z=[y(1),y(2),…y(m)]T
(6)
为使响应面模型得到最小预测误差,通过最小二乘法[12]求误差最小值,响应面数值与试验值误差ε为
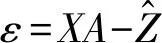
(7)
以待定系数向量A为变量,对式(7)进行误差平方求导,求得误差平方最小值,继而得到系数向量为
▽S(A)=▽(|ε|2)=▽(XA-Z)T(XA-Z)
=2(XA-Z)TX=0
(8)
A=(XTX)-1XTY
(9)
3 优化分析
3.1 台座参数化建模
桩是台座抗倾覆能力的集中体现,桩的位置,尺寸对于台座而言尤为重要,合适的牛腿位置也可有效地提高抗倾覆能力。
DM模块[13]提供了一个参数化驱动的建模方法,通过设定关键参数来达到优化分析的目的。如图5示,以模型最大主应力和变形量为目标函数,通过设置桩位置(A),桩半径(B),受力牛腿位置(C)和扩大基础高度(D)为变量进行优化分析。设计边量初始值和上下限如表2所示。
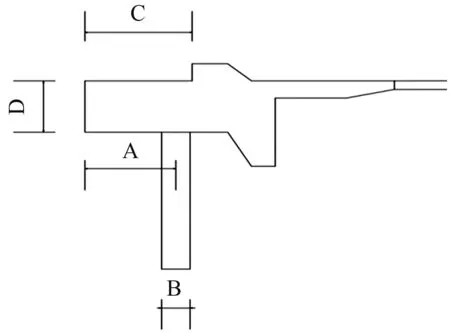
图5 设计变量图
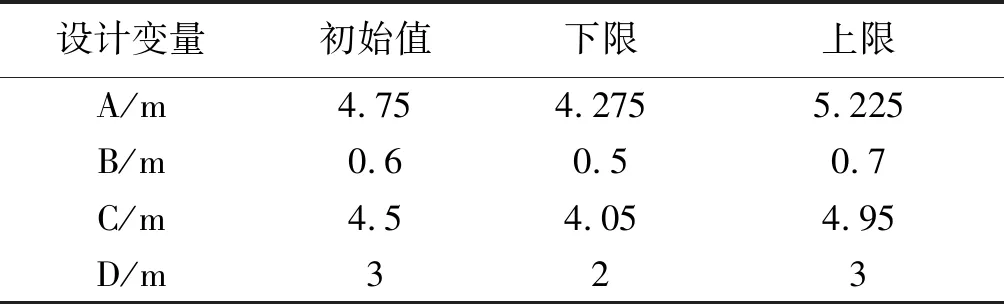
表2 设计变量初始值和限值
本文共计4个设计变量,中心试验重复次数取为1次,设计点个数为25个,借助于Design of Experiments[14]进行响应面试验设计,得到试验计算结果如表3和图6所示。
3.2 响应面分析
用Design Exploer[15]进行优化,得出求解设计点处的响应值,根据图7和图8所示,可以很直观地看出设计变量和目标变量的关系。
4 结果对比分析
为了与优化前结果进行比较,对优化后模型进行静态分析时,优化模型的前处理模块和优化前一致,分析结果如图9和图10所示。同样为了验证拓扑尺寸模型可行性进行对比分析。从表4可以看出:优化后的台座体积较优化前减少了,这在一定程度上减轻了自重,节省了材料的用量,而在后处理分析中,最大主应力减少了9.03%,最大变形量减少了29.9%,拓扑优化后结构性能有显著提升,在节省材料的同时性能也有所提升。

表3 试验设计变量计算结果

图6 试验设计变量计算结果图

表4 优化方案与原始方案对比
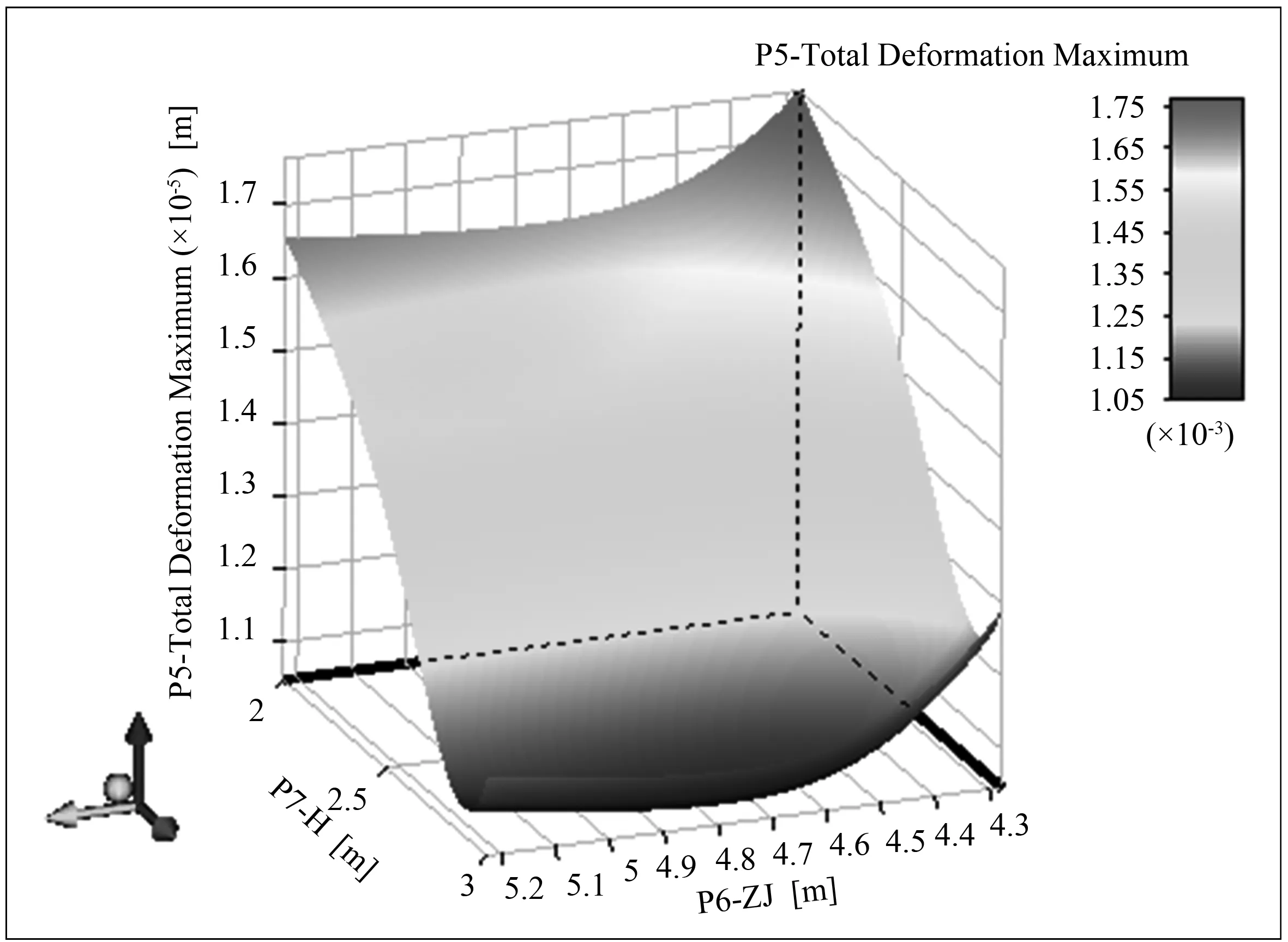
图7 桩位置和扩大基础高度与总变形3D响应图

图8 桩位置和扩大基础与最大主应力3D响应图
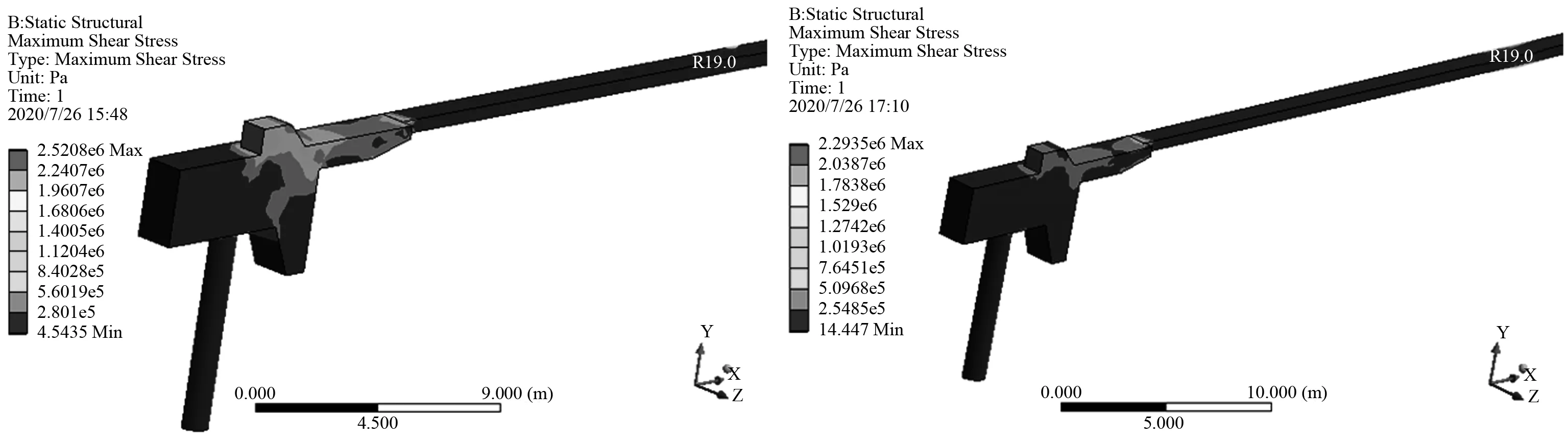
图9 最大主应力优化前后对比图
5 结论
利用ansys有限元分析软件分别进行台座形式确定、响应法理论推导和台座结构拓扑优化分析,得出如下结论:
(1)墩柱式台座与墩式台座相比的优点有:墩柱式台座在抗倾覆和抗滑移方面的性能具有明显的提高,同时它还具备了柱式长线台座不受线长限制的优点,因此墩柱式台座在实际工程中能够表现出更好的稳定性和便捷性。
(2)通过使用响应面法合理地选取试验点和迭代次数,可以保证试验数据的可行性和收敛性,在优化分析过程中利用全二阶多项式来逼近实际复杂的函数关系,经过一次次的迭代分析计算得出最优拓扑结构,然后得到受力分析的最优解。
(3)优化前台座承受的应力较大,经过结构优化之后台座的整体应力明显减少,因此在允许的范围内可以缩小台座的体积,减轻自重,节省材料,对于台座结构后续研究具有一定的参考价值。

