塑钢窗橡胶密封条老化后密封性能有限元分析*

王林林，王安迎，王 伟

(青岛科技大学 橡塑材料与工程教育部重点实验室，山东 青岛 266042)

橡胶密封条是塑钢窗密封的关键部件，可以起到有效的防尘、防水、减震、降噪、保温和密封作用[1]，综合性能优异，是近年来应用较广的新一代门窗密封条。塑钢窗橡胶密封条的密封性能主要来源于橡胶材料的高弹性与体积不可压缩性[2]，在使用过程中，密封条会发生热氧老化等现象，使其密封性能下降，产品的使用寿命降低。随着计算方法的发展，数值模拟在工业设计中的应用越来越广泛，具有成本低、周期短、效率高等优点，并取得了一定成效[3-4]。因此，借助有限元方法对塑钢窗橡胶密封条进行仿真分析，能够有效地评估产品的老化性能，预测密封性能的可靠性，具有重要的工程价值。

本文利用ABAQUS软件，对塑钢窗用橡胶密封条老化后的变形、应力分布及失效部位进行模拟，评价密封条老化后密封性能的可靠性。

1 塑钢窗橡胶密封条有限元模型建立

1.1 几何模型建立

根据塑钢窗橡胶密封条与金属框架之间的运动特点[5]，橡胶密封条工作时所受的外界载荷方向平行于其结构的横截面，可看作平面应变问题，为了节约计算时间，对其几何模型进行简化得到二维平面模型，所建立的有限元模型如图1所示。

图1 橡胶密封条的有限元分析模型

在进行网格划分过程中，橡胶密封条采用四边形杂交单元，共有752个节点，623个单元，能够得到较为精确的计算结果。

1.2 橡胶材料的本构模型

塑钢窗橡胶密封条常使用三元乙丙橡胶(EPDM)[6]，它可看作各向同性的、体积近似不可压缩的橡胶材料，在变形中体积变化极小，密封效果较好。因此，要选用超弹性本构模型来描述其非线性弹性行为[7-8]，金属框架可看作离散刚体。

为了提高计算结果的准确性，首先按照GB/T 3512—2001[9]，在120 ℃下对EPDM进行老化试验，老化时间分别为0 d、6 d、9 d、13 d、20 d和30 d。然后，对不同老化程度的橡胶试样分别进行单轴拉伸试验，利用得到的试验数据选取不同的本构模型进行材料参数拟合，最终选择了拟合精度最高的Yeoh本构模型。

该模型的应变能函数关系如式(1)所示[10]：

W=C10(I1-3)+C20(I1-3)2+C30(I1-3)3

(1)

式中：W为应变能密度，I1为第一格林应变不变量，C10、C20、C30为Rivlin系数。在应变较小的情况下，参数C10表示剪切模量；在应变中等的情况下，参数C20表示橡胶材料发生的软化现象，其值为负数；在应变较大的情况下，参数C30可以描述橡胶材料的硬化现象。

Yeoh本构模型在橡胶大变形条件下的模拟精度较高，它可以通过单轴拉伸试验得到的数据来进行材料的参数拟合，进而利用得到的拟合参数去预测其他变形的力学行为。该模型与橡胶的力学行为比较符合，并且具有形式简单等优点，应用广泛。

1.3 边界条件及加载方法

塑钢窗橡胶密封条在装配时，左侧与金属框架约束为固定状态，右侧为过盈装配，依靠其自身的过盈配合固定于工装上。对此工况下未老化的橡胶密封条进行有限元分析，可求得：当过盈量为1.985 454 mm时，密封条右侧所受到的支反力为28.3 N。

当关闭塑钢窗时，施加相同的外力，橡胶密封条的压缩变形量越大，表明其弹性性能越好，老化程度越低，密封效果越好。因此，使刚体与橡胶密封条右侧处于恰好接触的初始状态，然后对密封条右侧施加大小为28.3 N的载荷，再次进行有限元计算，得到密封条在120 ℃条件下，老化时间分别为0 d、6 d、9 d、13 d、20 d和30 d的变形情况。

2 结果与分析

2.1 应力分布分析

图2为在120 ℃条件下，老化时间分别为0 d、6 d、9 d、13 d、20 d和30 d时塑钢窗橡胶密封条在水平方向的应力分布云图。由图2可知，密封条的最大压应力主要分布于其两个凹槽部位，而其对侧的拉应力最大，这是由密封条的几何结构决定的，并且随着老化时间的推移，密封条在工作时所受到的最大应力也逐渐变大。拉应力越大的区域，越容易诱发裂纹，在长期使用过程中，该部位会过早老化，致使整个橡胶密封条出现早期失效。

图2 不同老化时间密封条的应力云图

2.2 变形量分析

图3为在120 ℃条件下，老化时间分别为0 d、6 d、9 d、13 d、20 d和30 d时塑钢窗橡胶密封条在水平方向的位移分布云图。由图3可知，密封条左侧与塑钢窗金属框架固定，变形量为0，密封条右侧在工作时受到水平方向的压力，为发生变形的主要区域。

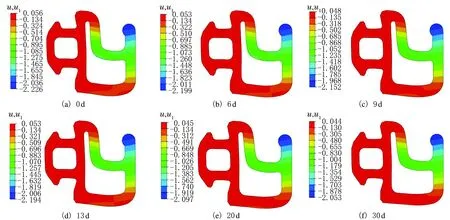
图3 不同老化时间密封条的位移云图

取右侧刚体的参考点来研究橡胶密封条的变形情况，可得到不同老化时间下密封条的压缩变形量，如图4所示。从图4可以看出，随着老化时间的延长，密封条的变形量呈线性减小趋势。这是由于随着使用时间的增加，在温度及空气中氧的共同作用下，密封条发生热氧老化现象，产生永久变形而变硬，弹性形变能力减弱，从而推断出塑钢窗橡胶密封条的密封性能变差，使用性能随老化时间的延长逐渐下降。

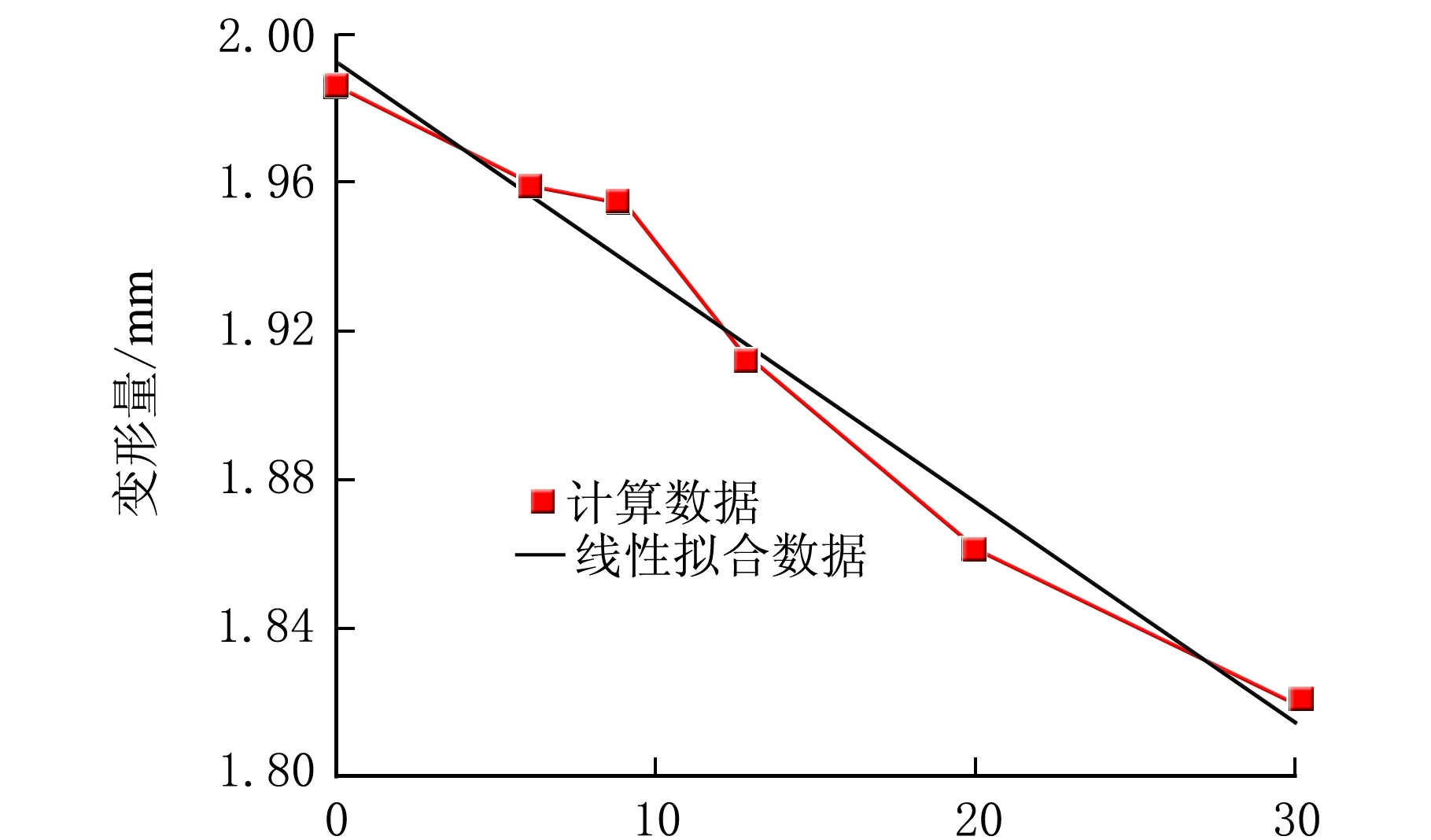
老化时间/d图4 不同老化时间密封条的变形量

2.3 接触压力分析

为了分析橡胶密封条与塑钢窗金属框架接触部位所受的接触压力，建立图5所示的接触路径。提取所建接触路径的计算结果，可以得到在120 ℃条件下，老化时间分别为0 d、6 d、9 d、13 d、20 d和30 d时塑钢窗橡胶密封条所受到的接触压力沿接触路径的变化曲线，如图6所示。由图6可知，在120 ℃条件下，老化时间分别为0 d、6 d、9 d、13 d、20 d和30 d时，塑钢窗密封条所受到的接触压力呈现基本相同的分布规律，密封条左侧下方与金属接触的部位所受到的接触压力最大。

图5 密封条接触界面上的压力分布及路径选取

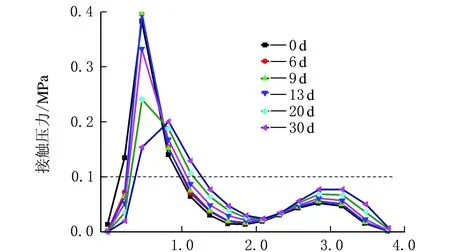
沿路径的真实距离/mm图6 不同老化时间密封条的接触压力沿路径变化曲线

从图6可以看出，随着老化时间的延长，橡胶密封条与塑钢窗金属部件的接触压力逐渐减小，且曲线呈驼峰状凸起，这是因为在密封条的左侧部位有一个橡胶支撑来提供密封条工作时的密封支撑力。

将不同老化天数密封条的接触压力进行对比，见表1。由表1可以看出，随着老化时间的延长，密封条受到的最大接触压力逐渐减小，接触压力的最大变化量为0.045 MPa，变化较小，密封性能基本稳定。塑钢窗橡胶密封条的密封属于界面接触密封，其内外部工作压力为大气压，不同老化时间的密封条接触路径上的平均接触压力大约在0.26 MPa，均大于0.1 MPa(即大气压)，且接触区域连续均匀。因此，在所研究的老化时间范围内，该橡胶密封条的老化程度较小，密封效果较好。

表1 不同老化时间密封条的接触压力

2.4 老化程度分析

根据GB 12002—1989[11]中对塑料门窗用密封条的规定，在老化温度为100 ℃、老化时间为72 h条件下，密封条所用橡胶的热空气老化性能的拉断伸长率保持率应在70%以上。

速率常数k与老化温度T之间的关系服从Arrhenius公式，如式(2)所示：

(2)

式中：A为频率因子，d-1；E为表观活化能，J/mol；R为气体常数，J/(K·mol)；T为老化温度，K。

因此，可得到两个不同温度下的加速系数计算公式，如式(3)所示：

(3)

式中：AF为加速系数；T1为非加速状态下的老化温度，K；T2为加速状态下的老化温度，K。

该加速老化试验是在120 ℃条件下进行的，由式(3)计算可得，当加速老化温度为120 ℃时，加速系数为3.470 675，换算成老化时间为0.864 385 d。

该橡胶密封条的老化寿命预测模型，如式(4)所示[12]：

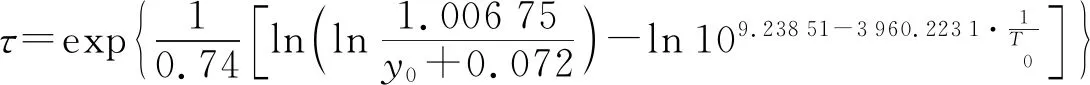
(4)

式中：τ为老化时间，d；y0为老化程度；T0为老化温度，K。

根据式(4)可计算得到老化温度为120 ℃，老化时间为0.864 385 d时，橡胶密封条的老化程度约为0.811 804，大于国家标准规定的0.7，比标准要求的老化程度偏小。这表明在所研究的老化时间范围内，橡胶密封条的密封性能较好，这进一步验证了利用有限元方法进行塑钢窗橡胶密封条老化后密封性能的分析是合理的。

3 结 论

(1)有限元方法可以较准确地预测老化后密封条的变形及应力，并结合老化寿命预测模型来评价密封条结构的密封性能。

(2)密封条凹槽区域为应力集中，易出现过早老化的部位。

(3)在相同关窗外力下，随着老化时间的延长，密封条的变形量呈线性下降，弹性减小，密封效果变差。但本研究中界面上的接触压力仍然高于大气压，并且拉断伸长率指标在高温老化后满足国家标准，表明该密封条满足标准规定的50年使用要求。