偶数维带边流形上的一类Kastler-Kalau-Walze类型定理

包开花, 孙爱慧, 夏令远

（1. 内蒙古民族大学 数理学院, 内蒙古 通辽 028000; 2. 吉林师范大学 数学学院, 吉林 四平 136000;3. 东北师范大学 数学与统计学院, 长春 130024）

0 引 言

非交换几何框架下的非交换留数是定义在闭流形经典拟微分算子代数上的迹, 但它不是通常算子迹意义下的延拓. 低维流形上的非交换留数是由Adler[1]发现的, 而高维流形的非交换留数是由Wodzicki[2]和Guillemin[3]同时发现的. Connes[4]敏锐地发现Dirac算子逆平方的非交换留数与Einstein-Hilbert作用成比例, 现称此结论为Kastler-Kalau-Walze定理(以下简称KKW定理). Kastler[5],Kalau等[6]分别独立地证明了此定理. 这开创了非交换几何框架下的非交换留数在重力作用方面的理论和应用, 为重力作用给出了一种算子理论解释, 赋予了KKW定理非平凡的研究意义.

Wodzicki的结论是: 当底流形为非紧致或带边流形时, 经典拟微分算子代数上不存在迹形式. 在带边流形的情况下, 需要考虑不同的代数结构. Fedosov等[7]将经典的非交换留数在Boutet de Monvel代数上进行推广, 得到带边流形上的非交换留数. Wang[8]将Connes的框架推广到带边流形情形, 得到了带边流形的共形不变量. 进一步, Wang[8-10]结合Ponge[11]的工作, 用带边流形上的非交换留数定义了与无挠Dirac算子相关的带边流形上的低维体积, 并得到了这种情况下的KKW类型定理, 对带边流形上的重力作用给出一种算子理论解释. 对于带挠率的Dirac算子不能直接利用Fedosov,Ponge等给出的方法得到紧致带边流形的低维体积. Ackermann等[12]在偶数维Spin流形上证明了带挠率的Dirac算子的Lichnerowicz公式. 近期, Pfäffle等[13]在配有保度量联络的紧致黎曼流形上考虑了带挠率Dirac算子的特征. 进一步, Pfäffle等[14]考虑了在紧致黎曼流形上带挠率的保度量联络的变化情况, 并结合诱导的Dirac算子、形变Dirac算子以及Chamseddine-Connes类型Dirac算子表示出了其谱作用. 在文献[15-16]中, 笔者将文献[8,13]中的结论进一步推广, 对紧致带边Spin流形给出了带挠率的Dirac算子相关的低维体积表示, 得到相应的KKW类型定理, 并导出了低维紧致带边Spin流形上的重力作用.

1 带边流形上关于带挠率的Dirac算子的低维体积

设 (M,gM) 是n=2n+2 维定向带边黎曼流形, 边界为∂M且配备有固定的Spin结构. 设M上的度量gM有下面的形式:

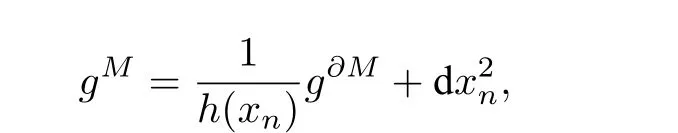
2 偶数维带边流形上的一类Kastler-Kalau-Walze类型定理

本章将构建一类KKW类型定理. 首先计算带挠率的Dirac算子的与本文相关的一些符号. 带挠率的Dirac算子的定义、符号及相关的详细内容请参看文献[15]中的第二节, 本章不再详细介绍相关的几何环境. 设 (M,gM) 是n=2n+2 维定向带边黎曼流形, 边界为∂M且配备有固定的Spin结构. 那么由文献[15]得出, 带挠率的Dirac算子DT定义为

其中

由文献[15]的结论可得如下引理.

其中

由文献[17]的引理3.1, 通过计算可得

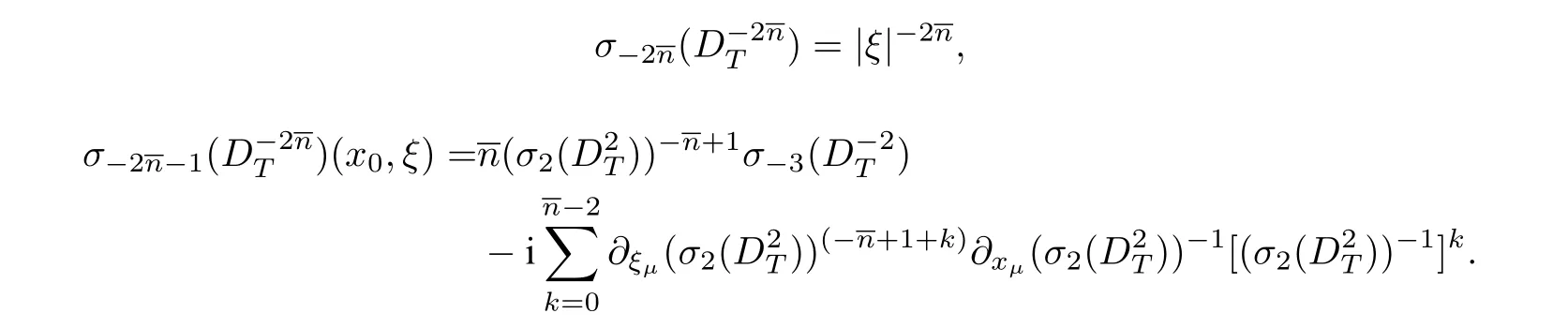
由拟微分算子的复合公式可得

则可得以下引理.

由引理2.1和引理2.3可得

由引理2.1和引理2.3可得

由引理2.2和引理2.3可得

由引理2.1及引理2.3—2.4可得

其中 Φ 由式 ( 2) 给出.

由定理2.5可得以下推论.