Bearing capacity of surface circular footings on granular material under low gravity fields

Pin-Qing Mo,Guoqing Zhou,Feng Go,Ruilin Li,*

a State Key Laboratory for Geomechanics and Deep Underground Engineering,School of Mechanics and Civil Engineering,China University of Mining and Technology,Xuzhou,221116,China

bSchool of Civil Engineering,Central South University,Changsha,410075,China

Keywords:Low gravity fields Bearing capacity Shallow foundation Planetary regolith simulant

ABSTRACT Low gravity fields have been simulated through magnetic acceleration to conduct experimental study on bearing capacity of circular footings on a type of crushable planetary regolith simulant,which has comparable density and particle size distribution of lunar soil.The load-settlement responses of surface spread footings are obtained by investigating the relative density,footing size and gravity effects.Applying the hyperbolic asymptote method,normalised foundation stiffness and ultimate bearing capacity are obtained by curve fitting and predicted by power functions using multivariate nonlinear regression.The results show that the nonlinear gravity effect is not negligible,related to stress condition,soil dilatancy and mobilised friction angle.A cone penetration test(CPT)-based method for prediction of bearing capacity is proposed with correlations between ultimate bearing capacity of footings and shallow penetration stiffness of CPTs,avoiding the uncertainties of soil property estimations.Analyses of allowable bearing capacity and footing influence zone in consideration of footing size and gravity effects could therefore improve the design of shallow foundations on the Moon and Mars,and provide new understandings and potential implications to the bearing capacity of shallow foundations on crushable granular material in both terrestrial and extraterrestrial geotechnical engineering.

1.Introduction

Since the recent space programs launched by USA (e.g.NASA’s InSight misson),China (e.g.Chang’e 4 mission),and many other countries (e.g.Russia’s Luna-Glob 1),the near-Earth space exploration has entered a new era from the Moon to Mars.As the spacecraft arrives at the surface of space colonies,they are controlled to land on a layer of soil with fine fraction of regolith.Following the deployment of stationary landers and adventure of rovers,further exploration tends to progress towards the creation of lunar or Martian bases,human habitats,and other types of space architecture.The stability of all these artificially created structures is significantly dependent on the interaction between foundations and planetary regolith under low gravity fields.Note that the gravity on the surface of the Moon is about 1.625 m/s2(g/6,where g is the Earth gravity,and g=9.8 m/s2),and the gravity on the Mars is around 3.711 m/s2(0.38g).

Shallow foundation is widely constructed to support a structure by transferring structural loads to the subsurface bearing material,and isolated bearing pads are currently adopted as the typical foundation of spacecraft (e.g.Lunar Module and Mars InSight Lander).Based on the depth of 776 bootprints from Apollo missions(boot size was about 125 mm in width and 330 mm in length,and the applied pressure was close to 7 kPa),the average modulus of subgrade reaction is approximately 8 kPa/cm,and its conservative value reduces to 2 kPa/cm with 95%confidence level(after Mitchell et al.,1972;Heiken et al.,1991).The modulus value was thus used for estimation of allowable bearing capacity with a given acceptable settlement.The analysis of bootprint pressure and settlement provided the early insights into the stiffness and bearing capacity of shallow foundation on the lunar surface.

Although the failure mechanisms of terrestrial shallow foundations have been studied extensively using analytical,numerical and experimental approaches,the effect of low gravity fields has not been adequately investigated.The static and dynamic penetration experiments under reduced gravity were performed using a drop tower with height of 6 m (free fall duration is about 1 s) by Perko and Nelson(2000)to show the pronounced effect of reduced gravity on the reductions in both initial peak resistance and progressive failure after the peak stress.Microgravity experiments conducted by Sture et al.(1998) and Alshibli and Hasan (2009)indicated that the shear strength parameters (friction and dilation angles)of lunar regolith are higher due to the reduced gravity environment.More recently,pressure-sinkage tests were conducted by Zou et al.(2015) using a low gravity simulation device along an inclined bin.The results indicated that the low gravity induced decrease in the shear strength of lunar regolith,and illustrated the low gravity effect on the mobility of lunar rovers.However,the current testing methods for creation of low gravity(through space station,satellite,space shuttle,microgravity rocket,parabolic flight aircraft,and drop tower) are either expansive or unstable,offering a very short duration of microgravity.

Alternatively,two types of lunar soil simulants,i.e.MLS-1(Perkins and Madson,1996a) and JSC-1 (McKay et al.,1994),were prepared in a very dense state to examine the bearing capacity of shallow foundation in a geotechnical centrifuge,with particular investigation of scale effect(Perkins and Madson,1996b).However,high gravity fields created by the centrifuge need to be corrected by the scaling laws for low gravity analyses(Lee et al.,2018).As to the analysis of centrifuge data,the gravity effect is usually coupled with size effect in consideration of stress level.With a simulated gravity n times the Earth gravity created by the centrifuge,the physical model can be treated as either a prototype with size n times larger than that on the Earth,or a prototype with size 6n times larger than that on the Moon (Mo,2019).The gravity and size effects are coupled for a centrifugal test with a certain scaling factor,and it is therefore not clear to examine the effect of gravity-induced stress gradient.

This paper aims to investigate the bearing capacity of circular footings on crushable granular material with particular interests on the effects of low gravity,footing size,and relative density using an alternative approach.The geotechnical magnetic-similitudegravity model testing (GMMT) method is adopted to simulate accurate and stable low gravity fields,which could provide insights into the gravity effect,uncoupled from the scale effects.The prediction of load-settlement response of circular footings is proposed for evaluation of foundation stiffness and ultimate bearing capacity.Applying the cone penetration test (CPT)-based foundation design method,the bearing capacity of shallow foundation is estimated from the cone penetration resistance,and the footing influence zone is obtained with varying relative density and gravity.

2.Bearing capacity of shallow foundation

The bearing capacity of shallow foundations has been extensively studied since the 1920s,and general equation for the ultimate bearing capacity proposed by Terzaghi (1943) is widely accepted with three bearing capacity factors,i.e.Nc,Nqand Nγ in terms of Mohr-Coulomb failure criterion,related to the cohesion c,surcharge q and unit weight γ,respectively.For the scenario of surface footings on cohesionless soil,the ultimate bearing capacity qultcan then be simplified as

where γ and ρ are the soil unit weight and density,respectively;B is the width of foundation;sγ is the Terzaghi’s shape factor,which is 0.6 for circular footings;and Nγ is the bearing capacity factor,which is originally related only to soil friction angle (Terzaghi,1943;Meyerhof,1963;Hansen,1970;Vesi´c,1973;Michalowski,1997;Zhu et al.,2001;Martin,2005).Conventional stability solutions also show that the bearing capacity factors are generally the exponential functions of friction angle.

However,the peak friction angle of soil is found to be strongly dependent on the confining stress and relative density (Bolton,1986),and the mobilised friction angle related to shear strain is not uniform under foundations and not consistent with various footing sizes.Correspondingly,the bearing capacity factor decreases with the absolute footing size,which has been investigated extensively in terms of ‘scale effects’ (Kimura et al.,1985;Kusakabe,1994;Herle and Tejchman,1997;Zhu et al.,2001;Ueno et al.,2001;Cerato and Lutenegger,2007;Loukidis and Salgado,2011;Lau and Bolton,2011).Scale effects of shallow foundation are mainly attributed to nonlinearity of failure envelope and progressive failure.As to material nonlinearity,larger footing is considered to carry higher stresses within the influence zone under the footing,and higher stress decreases both the peak friction angle and peak dilation angle within the failure zone owing to the curvature of material failure envelope.The bearing capacity factor Nγ is therefore suggested to decrease exponentially with footing size (Zhu et al.,2001).Additionally,particle size effect of granular material is considered to be negligible when the ratio of footing size (B) to mean particle size (d50) is greater than 30-100 (Ovesen,1975;Kusakabe,1994;Herle and Tejchman,1997).In terms of the phenomenon of progressive failure,soil under footings experiences strain localisation and shear strength mobilisation,which are heavily dependent on the soil relative density and effective stress confinement.The degree of progressive failure was reported to increase with footing size(Yamaguchi et al.,1976,1977),while the difference between the peak and critical state friction angles decreases with increasing mean stress level.Cerato and Lutenegger (2007) conducted model-scale footing tests to further evaluate the scale effects of shallow foundation on granular material,as well as the effect of relative density.Gravity effect was typically considered as a subordinate factor of scale effect that affects the stress level,whereas the gravity-induced stress gradient seemed to be more intrinsic for the bearing capacity of shallow foundation.Previous studies usually combine the gravity and size effects using small-scale physical modelling or centrifuge modelling,by applying the scaling laws based on the assumption of continuum.To simulate a shallow foundation on the Moon surface,the physical model on the Earth should be scaled up by 6 times (i.e.ratio of the Earth gravity to the Moon gravity),to model the corresponding stress field.However,it is questionable to simply take the bearing capacity of footings on the Earth as that of footings with 6 times larger size on the Moon avoiding the particle size effect.Therefore,the gravity effect needs to be further investigated apart from the scaling approach,as will be discussed in the following sections.

3.Geotechnical low gravity model testing

Physical modelling of loading tests of shallow foundation is conducted in this study,with particular concerns on size and low gravity effects.To provide a stable low gravity field (modelling gravity gmis smaller than the Earth gravity g,i.e.the acceleration factor Ng=gm/g<1,which is also taken as g-level)with a reliable and economical testing method,GMMT was recently proposed by applying a magnetic acceleration in the opposite direction to the Earth gravity (Li et al.,2019;Mo et al.,2019).Fig.1a shows the corresponding testing equipment,including testing container,power supply system,cooling system,control system and data acquisition system.Two groups of copper coils were installed within the testing container to provide a uniform magnetic field(UMF)and combined gradient magnetic field(CGMF),respectively,as illustrated in Fig.1b.The UMF coil is to provide a uniform magnetic field based on the Biot-Savart law and to realise the saturated magnetisation of the magnetic material.The CGMF coils,a pair of reverse current parallel coils,create a centrosymmetric and linear gradient magnetic field,providing stable magnetic force to the saturated-magnetised material (after Li et al.,2019).

Fig.1.The GMMT equipment and testing apparatus.

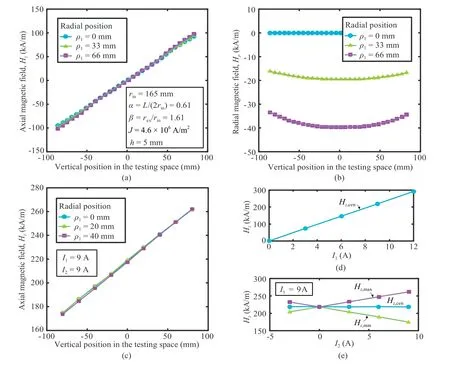
Fig.2.The uniformity and gradient of magnetic field intensity within the testing space.

The uniformity of the magnetic force at the centre of the testing container has been verified theoretically and experimentally,as shown in Fig.2.After separating the CGMF coil into layers with gap h=5 mm(inner radius of coil rin=165 mm,ratio of length to inner diameter α=L/(2rin)=0.61,outer-inner diameter ratio β=rex/rin=1.61,and Ampere density J=4.6 ×106A/m2),the calculated axial and radial magnetic fields along the vertical position of testing space are depicted in Fig.2a and b,respectively,based on the electromagnetic field theory.The axial magnetic field intensity varies linearly with the vertical position,which can provide a constant gradient for a stable magnetic force along the axial direction,while the radial magnetic field intensity generally maintains a uniform distribution.The radial gradient of the radial magnetic field still exists that could introduce unexpected radial force.However,compared to the vertical gradient of axial magnetic field,the magnitude is relatively limited resulting in acceptable disturbance,and further attempts are also desired to eliminate the radial gradient of magnetic field,as reported by Li et al.(2019).Experimentally,by applying magnetising current I1=9 A to the UMF coil and magnetic force current I2=9 A to the CGMF coil,the measured axial magnetic field also shows a linear increase with the vertical position (Fig.2c).The variations of axial magnetic field intensity with both I1and I2were also tested and are presented in Fig.2d and e,respectively,and the linear trends again indicate the uniformity of magnetic field within the testing space.More detailed verification and explanation can be found in Li (2018) and Li et al.(2019).Following this method,a reliable gravity field varying from 0g to 6g can be simulated within the testing space of φ 90 mm × 180 mm (after Li et al.,2019).

Planetary regolith is a type of granular material with distinctive mineralogy and morphology under a unique space weathering environment.Regolith simulants were produced to replicate the mineral composition and breakage process to obtain comparable physical and mechanical properties(e.g.McKay et al.,1994;Perkins and Madson,1996a;Zheng et al.,2009).However,in order to satisfy the testing conditions using GMMT,magnetic sensitivity is the primary characteristic of granular material,and a magnetic-type planetary regolith simulant is therefore required.By mixing cement (type of 62.5R),iron oxide powder (type of BMMF-1),and water with a ratio of 1.25:1.25:1 by weight,slurry cubes were cast in 100 mm cube moulds and cured for 28 d,which was then smashed by a hammer into granular material with particle size smaller than 1 mm.The aggregation of simulant particles is shown in Fig.3a,and the angle of repose seems to be around 42°.Fig.3b presents the representative particle shapes from two-dimensional images,and analyses of sphericity and roundness were conducted following the method of Zheng and Hryciw (2015).The Wadell’s roundness,which is defined as the ratio of the average radius of curvature of the corners of a particle to the radius of the maximum inscribed circle (after Wadell,1935),varies from 0.27 to 0.56.The average area sphericity is about 0.69,and the width to length ratio of the sphericity ranges from 0.62 to 0.96,following the definitions of Zheng and Hryciw (2015).

In order to guarantee the uniform magnetic sensitivity,the mineral composition of typical lunar soil is not recovered,and the cemented granular material seems to be relatively crushable.However,agglutinates (glass-bonded aggregates) are normally formed at the surface of lunar soil with dynamic processes of comminution and agglutination,which also indicate the maturity of lunar soil(Heiken et al.,1991).As vesicles are commonly present in agglutinates,the irregular particles are relatively crushable,and it has been noted that the lunar soil is more compressible than current simulants due to the crushing of agglutinates under loading(Heiken et al.,1991;Khademian et al.,2019;Marzulli and Cafaro,2019).The current planetary regolith simulant is thus used to examine the mechanical behaviour of crushable granular material.To evaluate the particle strength,the maximum load Ffof the particle tensile strength test is used to calculate the tensile strength σfin terms of grain diameter d(after Lee,1992;McDowell and Bolton,1998),as illustrated in Fig.4a.The decrease of particle mean tensile strength with the average particle size is depicted in Fig.4b,showing that both the strength and size effects of the regolith simulant are less than those of the Oolitic limestone.It suggests that the granular material is highly crushable (probably about one order of magnitude more crushable than that of the actual regolith),and therefore,the load tests on shallow footings in this study may result in particle breakage,which would accelerate soil deformation.

In terms of a single grain of regolith,the magnetic force acts only on the magnetic substance.If the iron oxide powder is distributed uniformly within the grain,the magnetic force on the grain is ideally analogous to the Earth gravity.Micro-moments on particle might exist when the powder is not uniformly distributed within the grain.Considering the size of magnetic powder of around 5-10 μm,the process of mixing and curing results in a relatively uniform material,and the effect of micro-moments is thus limited compared to that of the magnetic force.Using the applied magnetic force,the simulated gravity is therefore obtained by combining the magnetic acceleration and the Earth gravity,as illustrated in Fig.5a.The magnetisation characteristic curve of the planetary regolith simulant was obtained to evaluate its specific saturated magnetisation and critical magnetisation field,by applying the magnetising current I1to the UMF coil.The magnetic force current I2was then applied to the CGMF coils to generate the linear gradient magnetic field for creating the magnetic force and thus the low gravity.By measuring sample weight with varying I2from three repeatability tests,the magnetic property of regolith simulant was obtained with the relationship between the magnetic force current I2and the acceleration factor Ng,giving Ng=1-0.361I2,as shown in Fig.5b.With this relationship,we can simulate any low gravity by changing the magnetic force current after the material is saturatedmagnetised (Li et al.,2019;Mo et al.,2019).

Fig.3.(a) The planetary regolith simulant and (b) its particle shapes.

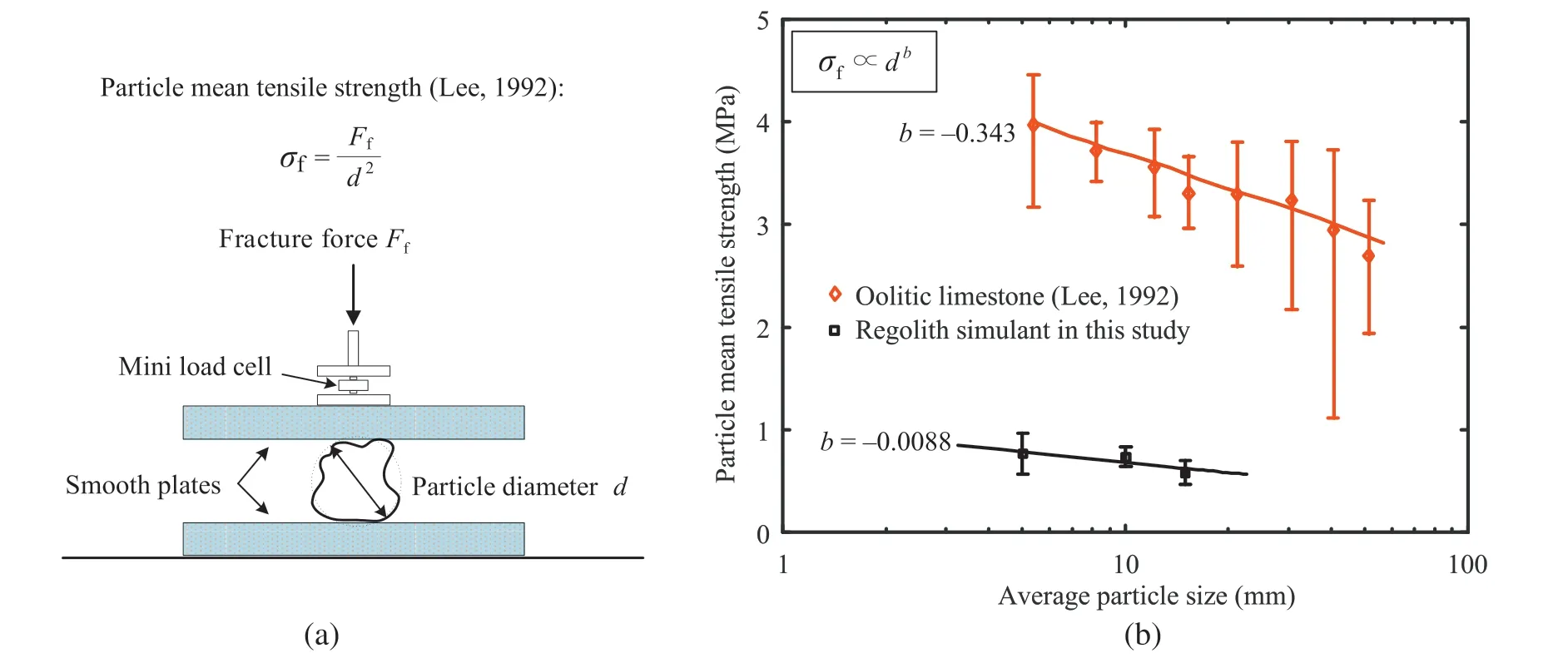
Fig.4.Particle strength of the planetary regolith simulant.

Fig.5.(a) Simulated g-level and (b) its relationship with the magnetic force current.

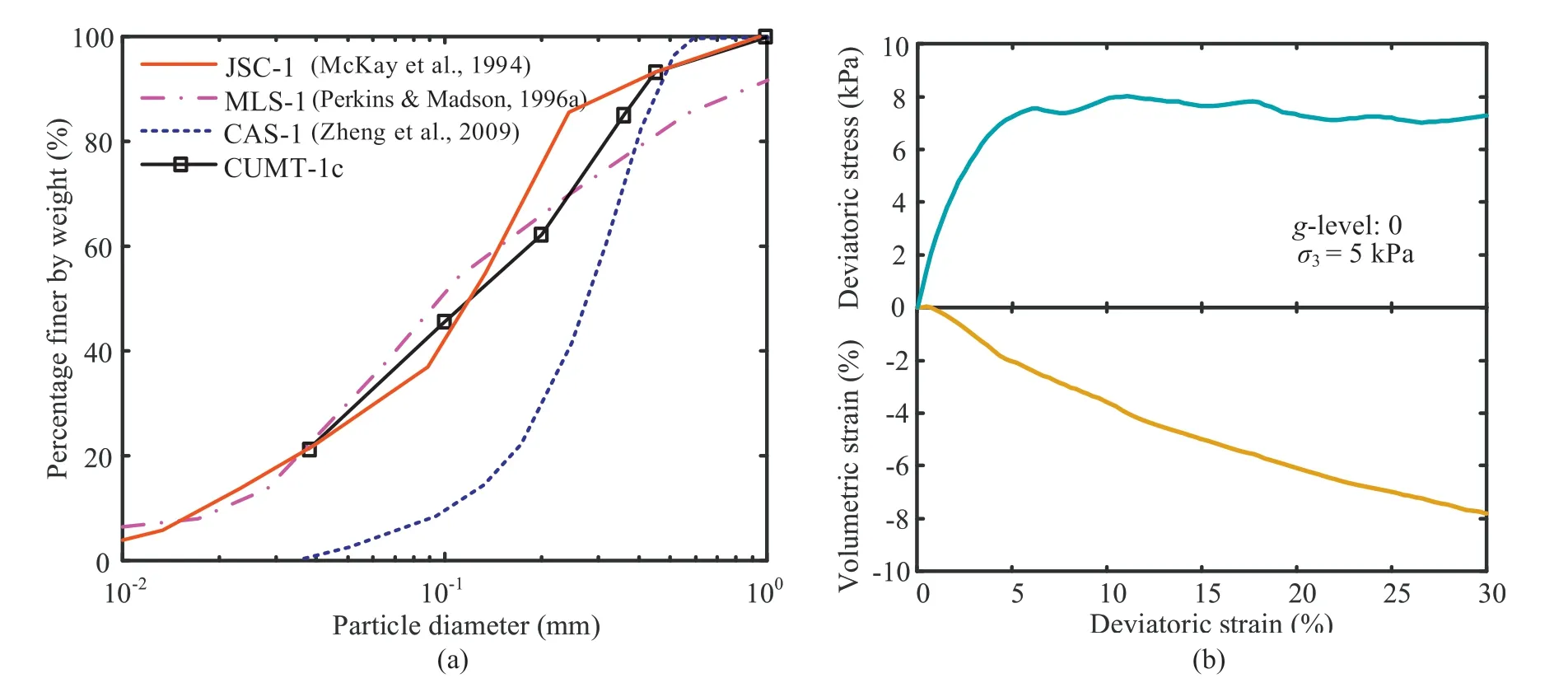
Fig.6.(a) Particle size distribution curves of regolith simulants,and (b) the results of triaxial compression test.

The magnetic regolith simulant was prepared by controlling the particle size distribution curve in comparison with other regolith simulants,e.g.JSC-1 (McKay et al.,1994),MLS-1 (Perkins and Madson,1996a),and CAS-1 (Zheng et al.,2009),as shown in Fig.6a.This type of crushable planetary regolith simulant was termed as CUMT-1c,and the fundamental physical properties of CUMT-1c are listed in Table 1 with comparisons of lunar soil according to the available data from the literature.

The conventional drained triaxial compression tests on crushable regolith simulant with density of 1.3 g/cm3was reported by Mo et al.(2019),and the typical stress-strain curves at 5 kPa of confining pressure for CUMT-1c under 0g environment (i.e.the magnetic and gravity forces have the same magnitude,and Ng=0)are depicted in Fig.6b.It should be noted that the obtained friction angle is relatively low,which is attributed to the particle breakage during triaxial test.Cecconi et al.(2002) reported that grain crushing can induce a reduction in the frictional properties of the material.Based on the triaxial tests with confining pressure varying from 5 kPa to 30 kPa and simulated gravity varying from 0g to 1g,the unique critical state line in terms of decreasing void ratio with stress level was proposed as e=-0.061lnp+1.538(after Mo et al.,2019).

Compared with other lunar regolith simulants,the granular material used in this study has some intrinsic limitations.The mineralogy of lunar regolith was not simulated,as the GMMT requires the magnetic sensitivity of material.Despite the physical properties are comparable between the simulant and lunar soils(Table 1),the compressive strength of the siliciclastic framework grains in CUMT-1c is therefore much lower than those of basalt and breccia grains,and CUMT-1c can only be treated as a crushable planetary regolith simulant representing immature agglutinates with vesicles.Additionally,although the particle shape of regolith simulant is generally acceptable,the breakage method using hammer resulted in more spherical particles,especially for fine grains,compared to the sharp angularity of lunar soil particles under extreme space environment,with spallation,vaporisation and radiation damage.The approach of sintering using mixture of cinerite,magnetic powder and pore former would be a more suitable method for producing the regolith simulant,and a pneumatic breaker could be suggested to improve the angularity of particles.However,the specific gravity and particle size distribution were controlled to be comparable with lunar soil,and CUMT-1c was generally considered as an appropriate crushable granular material under low stress condition in GMMT.

In this study,the crushable planetary regolith simulant CUMT-1c is adopted to investigate the bearing capacity of shallow foundation under various low gravity fields,as depicted in Fig.7a.Three testing series were carried out to examine the effects of footing size,relative density,and gravity,as listed in Table 2.Series I-B is taken as the reference test for shallow foundation,which is identical to Series II-A and III-A.The testing procedure is briefly described as follows:

Table 1Parameters of planetary regolith simulant CUMT-1c and lunar soil.

(1) Sample preparation was carefully conducted with quartered layers in a container with 86 mm inner diameter by controlling the target relative density of each layer with air pluviation and tapping approach for compaction,and the prepared sample height was about 180 mm (sample size is limited owing to the effective testing space with uniform low gravity fields in the GMMT equipment,as can be found in Fig.2).

(2) Circular footing with a smooth base,manufactured from aluminum alloy to avoid the influence of magnetic field,was placed on the surface of granular material and then vertically loaded at a velocity of 0.007 mm/s,with measurements of footing pressure and settlement.

(3) The termination of tests was set at around 3.2 mm of footing settlement,providing normalised settlement s/B over 15%.

(4) In order to verify the repeatability and reliability of loading tests,each series was repeated by 2-4 times for analysis.

The termination of tests at 3.2 mm of footing settlement was determined by the following reasons:

(1) The normalised settlement is 32%,21% and 16% for three types of footings,and the settlement at 10%of footing size is typically used to determine the bearing capacity of shallow foundation.

(2) Larger settlement indicates penetration into soil,and the height of footing (3 mm) would affect the penetration resistance for shallow foundation.

(3) Peak value of load was not expected even with larger settlement,due to the crushing or abrasion of regolith simulant under compression and the low gravity field/stress condition.Considering the relative sizes of footings and container,Bcontainer/B varies between 4.3 and 8.6,indicating the limited boundary effects of footing tests.

The CPT under low gravity fields is also conducted in this study for the interpretation of soil properties.A miniature penetrometer with a diameter of BCPT=8 mm and an apex angle of 60°,also manufactured from aluminum alloy,is pushed down to a depth of 100 mm from surface at a constant and slow speed of 0.25 mm/s for quasi-static loading tests,as illustrated in Fig.7b.The particle size and boundary effects are negligible with BCPT/d50=66.7 and Bcon-tainer/BCPT=10.8,as suggested by Bolton et al.(1999).The diameter of penetrometer shaft was manufactured as 6 mm,and the shrunken shaft design aims to neglecting the shaft friction by relaxing the soil around the probe shoulder.Table 3 presents the testing series of CPT in regolith simulant,investigating the effects of relative density and gravity field.Similarly,Series IV-C is taken as the reference test for CPT,which is identical to Series V-A.Additionally,the regolith sample preparation for CPT was identical to that for circular footing tests,and the measured CPT data are thus potentially used for the prediction of bearing capacity of shallow foundation.

4.Results of loading tests

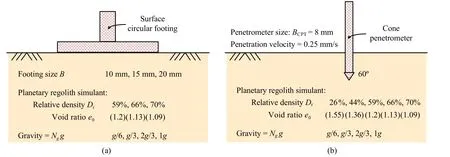
Fig.7.Schematics of model testing:(a) Surface circular footing;and (b) Cone penetration test.

The results of loading tests of surface circular footings on the crushable regolith simulant are presented in this section,with focus on the effects of footing size,relative density and low gravity field.The examples of testing data are provided in Fig.8,for both Series II-C and Series III-C.Repeatability tests are distinguished by colours,and the scattered data are largely attributed to relatively weak signal with regard to the 10 kg load cell,which is located above a long aluminum loading bar to avoid the influence of magnetic field(see Fig.1b).From the nonlinear load-settlement responses,the gradual increase of footing pressure with the settlement s can be clearly observed.Before the termination of loading test at 3.2 mm settlement,there is no obvious peak value for the direct determination of bearing capacity,and similar trends were also reported for local shear failure of shallow foundation by Vesi´c (1973),and for pile in crushable sands by Yasufuku and Hyde (1995).For estimation of bearing capacity of shallow foundation,failure criteria have been proposed according to the measurements,including Hansen(1963)’s method,de Beer (1970)’s method,hyperbolic asymptote(Chin,1971),pseudo-strain (10%) criterion (Amar et al.,1994),and zero stiffness method(Decourt,1999).In this study,the method of hyperbolic asymptote (Chin,1971) is adopted due to its simplicity and clear physical meaning of two parameters.Therefore,the loading curve (qbvs.s/B curve) is described using a hyperbolic relationship:

where qbis the footing pressure;s/B is the pseudo-strain;kiis the slope of the qbvs.s/B curve,representing the foundation stiffness;and qultis the asymptote of the hyperbola,indicating the ultimate load.Note that the shear modulus G can also be related to the foundation stiffness,following the Boussinesq’s equation as G=kiπ(1-ν)/8,where ν is the Poisson’s ratio.Each experimental test was evaluated for the determination of foundation stiffness and ultimate bearing capacity by curve fitting using Eq.(2),as illustrated in Fig.8.The fitting parameters for all tests are presented in Table 4,showing that both kiand qultgenerally increase with footing size,relative density,and g-level.The root-mean-square error (RMSE) and the coefficient of determination (R2) were used to evaluate the goodness of curve fitting for footing pressure qb.When the predictions perfectly fit the data,RMSE=0 and R2=1.Despite the fluctuation of measured data and variation between repeated tests,Eq.(2) generally provides a good estimation of loading response of shallow foundation.It is noted from Fig.8 that both foundation stiffness and ultimate load of footing on denser soil with Dr=70% (e0=1.09) are over 2.5 times higher than those of footing on soil with Dr=59%(e0=1.2),even though the gravity is smaller for denser soil test.It indicates that the relative density has a significant influence on the footing pressure,especially for surface footings with low stress condition and for crushable aggregates.

On the other hand,due to the wide range of void ratio for the material with different particle arrangements,a small change of relative density can result in a relatively large difference in void ratio.For instance,the soil with Dr=59% has a void ratio of 1.2,whereas e0=1.09 for the soil with Dr=70%.The difference in void ratio could have significant impact on geometric arrangement of particles and soil compressibility,as noted from one-dimensional compression test on compressible sands (after Yamamoto et al.,2008).

Both ultimate bearing capacity and stiffness of shallow foundation are considered to be strongly related to the relative density of soil Dr,footing size B,and g-level Ng(i.e.stress gradient).Note that these three components are not intrinsic and independent factors causing the scale effects,while they are apparent and easy to be determined in practice.Therefore,the relative density Drand corresponding normalised forms B/d50and γB/Prefare treated as the pronounced factors,and power functions (Lee et al.,2018) are adopted for predictions of foundation stiffness and ultimate bearing capacity with the following expressions:

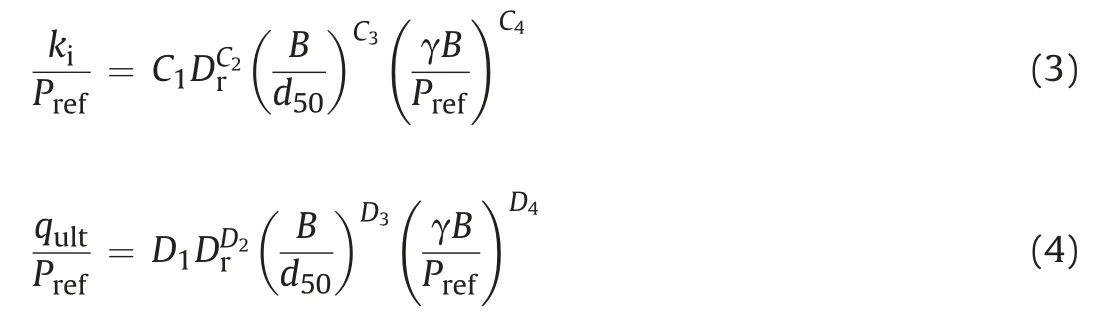
where Prefis the atmospheric pressure(100 kPa),which is taken as the reference pressure to normalise stress and stiffness;and C1-C4and D1-D4are the fitting parameters.It should be noted that the unit weight is related to the relative density (i.e.void ratio) and gravity as follows:

where ρwis the water density at 4°C.

Taking the normalised settlement s/B,relative density Dr,footing width B and acceleration factor Ngas four independent variables,the multivariate nonlinear regression was adopted to provide the optimal solutions of fitting parameters C1-C4and D1-D4,as shown in Table 5.For each test,the predictions of foundation stiffness and ultimate bearing capacity using Eqs.(3)and(4)are compared with the corresponding curve fittings in Table 4.The evaluation of nonlinear regression is provided in Fig.9,by comparing the predicted kiand qultwith those obtained from curve fitting of single test.The regression provides generally good predictions of both foundation stiffness and ultimate bearing capacity for soil with Dr=60%-70%(e0=1.09-1.19).Note that the in situ relative density of lunar soil was reported as around 65% in the top 150 mmaccording to Heiken et al.(1991).Compared to the experimental data of footing pressure against settlement,the overall goodness of prediction is evaluated as RMSE=2.25 and R2=0.82,indicating the satisfactory regression analysis.Note that the parameters were obtained based on the particular model tests on granular simulant,and cares should be taken for extrapolations.

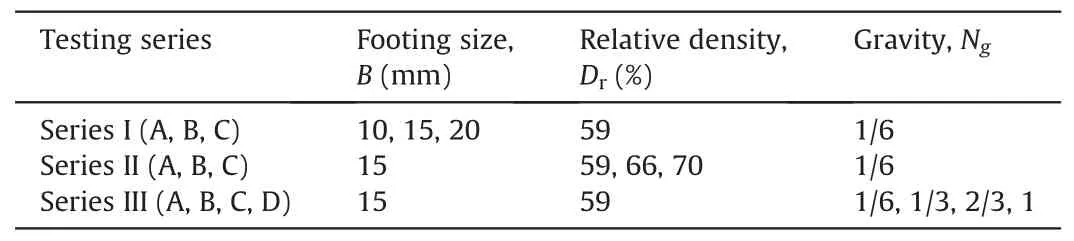
Table 2Testing series of circular footings on regolith simulant.

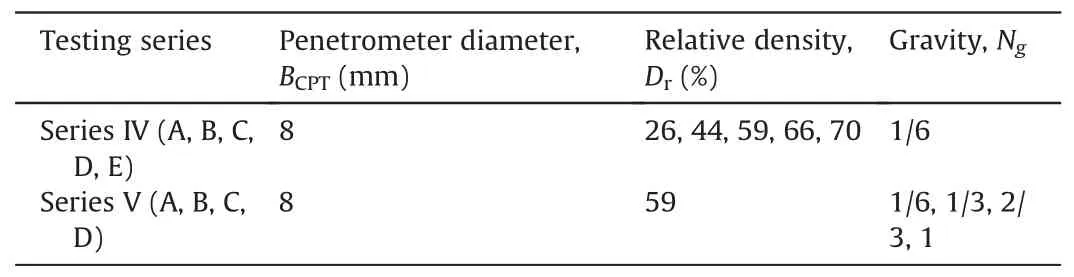
Table 3Testing series of CPT in regolith simulant.

Applying the predicting equations (Eqs.(3) and (4)),the loadsettlement responses of all testing series are presented in Fig.10,with varying footing size,relative density,and gravity,respectively.Note that the data discreteness of each test is attributed to nonuniform soil sample,signal fluctuation with low resistance and repeated testing data,although the repeatability is fulfilled and the trends are reasonable.The obtained responses could generally provide both qualitative and quantitative analyses of shallow foundation under various low gravity fields.Considering the wide range of void ratio and the crushable nature of granular material,the soil compressibility tends to be sensitive to the value of relative density.And it is arguably reasonable to note that the magnitude of foot pressure varies significantly for soil with Dr=60%-70%(e0=1.09-1.19).

Following the concept of bearing capacity factor after Terzaghi(1943),the Nγ factor for circular footings is provided as Nγ=qult/(0.3γB),which can then be expressed in the following way:

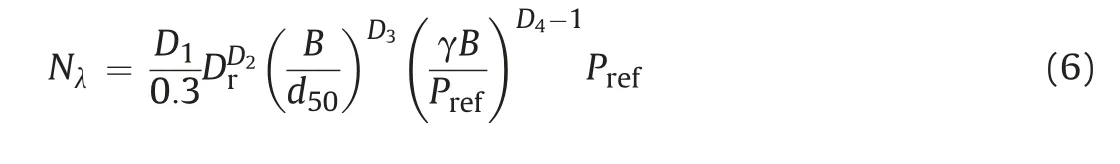
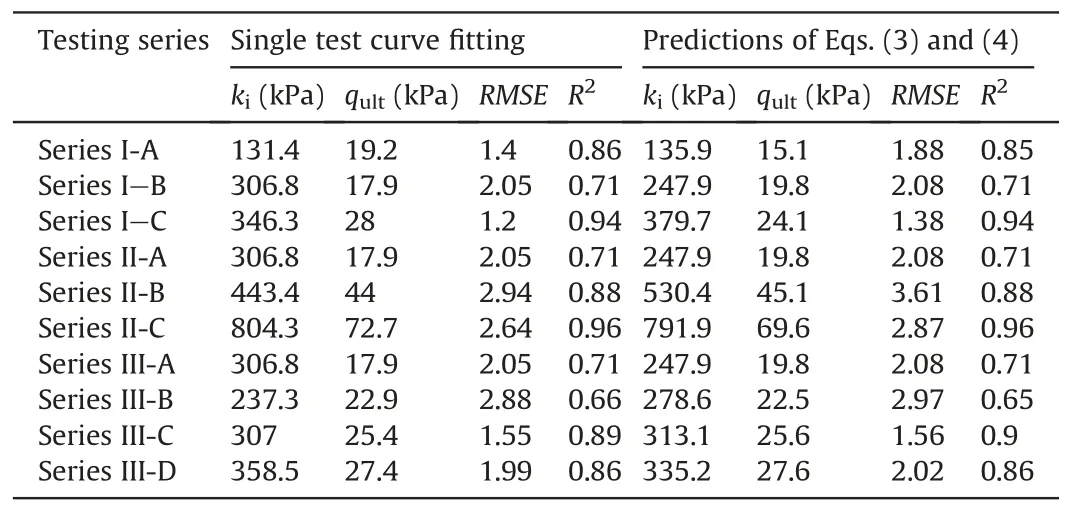
Table 4Curve fittings and predictions of foundation stiffness and ultimate bearing capacity with evaluations for all surface footing load tests.

Table 5Parameters obtained from nonlinear regression for predictions of foundation stiffness and ultimate bearing capacity.

From the parameters D2,D3and D4in Table 5,it can easily find the significant growth of bearing capacity factor with relative density,owing to the large value of D2.The decrease of Nγ with footing size is shown in Fig.11a for tests in soils with Dr=60%and Dr=70%.Compared to the effect of footing size(i.e.combining the exponents of B in Eq.(6)gives D3+D4-1=-0.319),gravity has a more pronounced influence on the bearing capacity factor,with an exponent of γ as D4-1=-0.816.Furthermore,the mobilised friction angle can thus be back-calculated through the formulae suggested by Prandtl (1921),Reissner (1924),Martin (2005) and Loukidis and Salgado (2011),that is,Nγ=（Nq-0·6）tan（1·33φ）and Nq=eπtanφtan2(π/4+φ/2).The mobilised friction angle was also termed as the ‘equivalent’ or ‘average’ friction angle by Loukidis and Salgado(2011),which includes the effects of material anisotropy and progressive failure.Correspondingly,the trends of mobilised friction angle with varying footing size and gravity are predicted,as shown in Fig.11b.It is noted that the back-calculated friction angle is much higher than the critical friction angle obtained from triaxial tests.As reported in Loukidis and Salgado(2011),the magnitude of φ shows a decreasing trend with footing size,as the larger influence zone under the base of foundation contributes to the higher mean stress condition,which causes the degradation of mobilised friction angle.On the other hand,the glevel has a direct impact on the stress condition,which restricts soil dilatancy and leads to smaller mobilised friction angle,showing the nonlinear gravity effect.

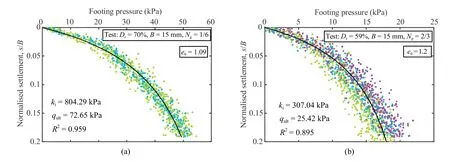
Fig.8.Load-settlement responses of circular footings:(a) Series II-C,and (b) Series III-C.Repeatability tests are distinguished by colours.

Fig.9.Evaluation of nonlinear regression:(a) Prediction and curve fitting of ki;(b) Prediction and curve fitting of qult;(c) R2 of predictions and curve fittings;and (d) RMSE of predictions and curve fittings.

5.CPT-based prediction of bearing capacity

The bearing capacity of shallow foundation is largely influenced by the significant uncertainties associated with Nγ and mobilised friction angle.A CPT-based method is therefore suggested for the prediction of qult,which could avoid the estimation of soil properties and their uncertainties (Lee and Salgado,2005).The cone penetrometer is pushed through soil layers,and the CPT data can directly reflect the mechanical behaviour of subsurface materials in some ways.

Corresponding to the footing tests on regolith simulant under low gravity,the results of CPTs are presented in Fig.12,with examination of the effects of relative density and gravity(as listed in Table 3).The penetration resistance qcgenerally increases linearly with penetration depth z at the initial stage of shallow penetration(z/BCPT<2.5).For deeper penetration,the growth of penetration resistance tends to slow down to a stable value,which is presumably attributed to the low stress condition,crushable particles and shrunken penetrometer.Similar trend was also reported from centrifuge numerical modelling of penetration tests on calcareous sand(McDowell and Bolton,2000;Zhang et al.,2013).The regolith simulant with its relatively low particle strength under low gravity in this study tends to have stable penetration resistance at a certain depth,and particle breakage is believed to be significant during penetration.The shrunken penetrometer shape would also weaken the increase of penetration resistance with depth,whereas this effect was found not dominant.From the results,it is concluded that penetration resistance is significantly dependent on the relative density,and the g-level can increase the magnitude of qcslightly.The repeatability of CPT in the GMMT apparatus has been shown in Mo et al.(2019),and the results of an additional test with an unshrunken penetrometer in soil of Dr=59%(e0=1.2)under g/6 are presented in Fig.12,in comparison with those of Series IV-C/VA.The penetration resistance is slightly higher than that of shrunken penetrometer test,since the stress around the shoulder of penetrometer is not released and results in higher shaft friction.However,the comparable results in turn verify the repeatability of CPT under low gravity field.

For the application of shallow foundation using CPT data,the shallow penetration is more important to reflect soil behaviour around the footings.The gradient of qcover normalised depth during the shallow penetration stage is defined as the CPT stiffness,i.e.ki,CPT=qc/(z/BCPT).Its variation with the relative density and glevel is described as follows,in a consistent form as kiand qultin Eqs.(3) and (4),respectively:where the parameters E1,E2and E3are obtained from nonlinear regression as follows:E1=4.084,E2=4.181,and E3=0.082.For the regression,RMSE=6.62,and the overall R2=0.93 compared to the experimental raw data.Note that the penetrometer of CPT normally has a standard size,and thus the effect of penetrometer size is not included in this study.

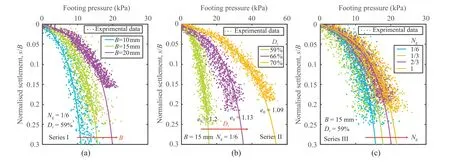
Fig.10.Predictions of load-settlement responses:(a) Footing size effect;(b) Relative density effect;and (c) Gravity effect.

Fig.11.Back-calculations of (a) bearing capacity factor and (b) mobilised friction angle.

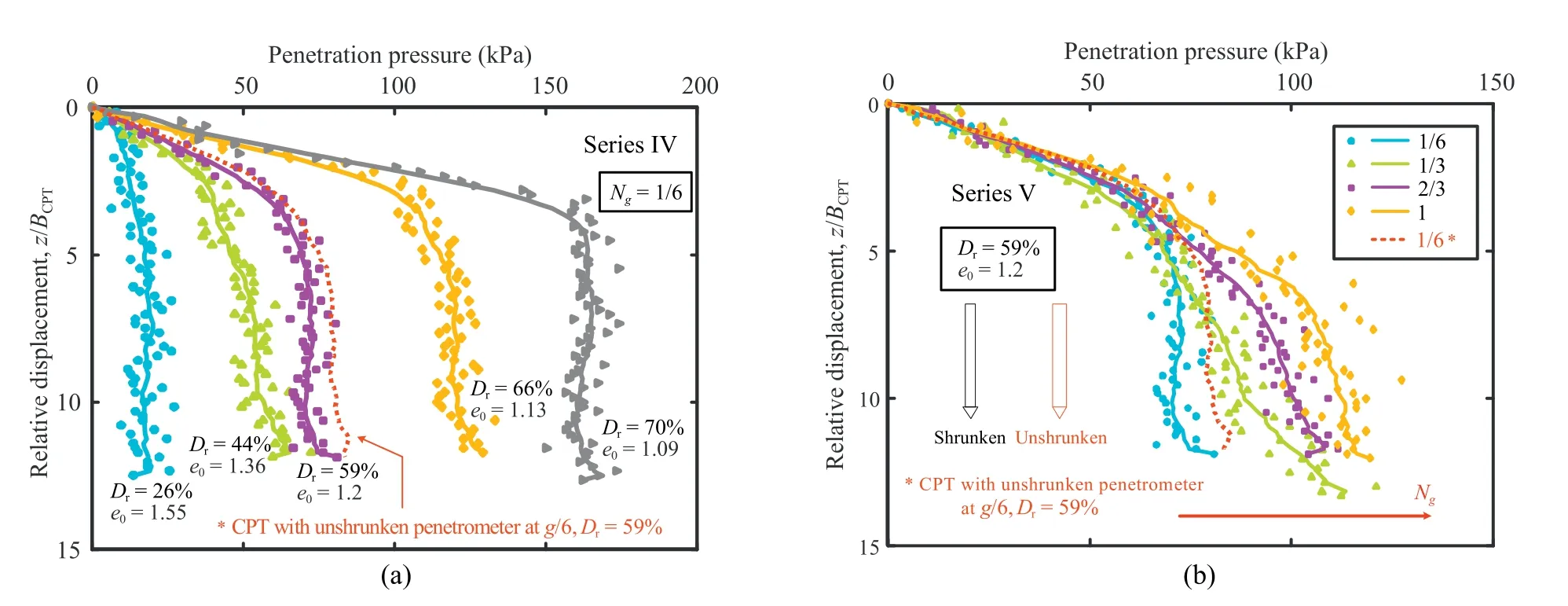
Fig.12.Penetration resistance against depth:(a) Relative density effect;and (b) Gravity effect.

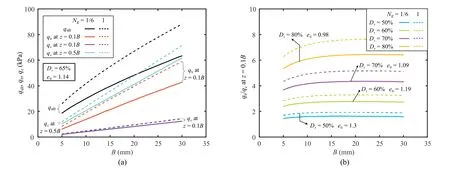
Fig.13.Comparisons of bearing capacity and penetration resistance:(a) Penetration depth effect;and (b) Resistance ratio.

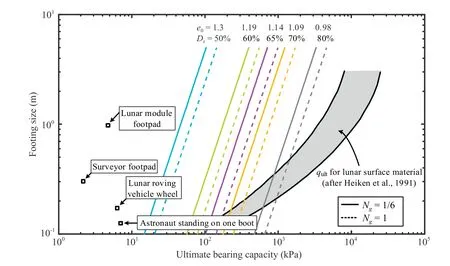
Fig.15.Relations of footing size and ultimate bearing capacity on the Moon and Earth.

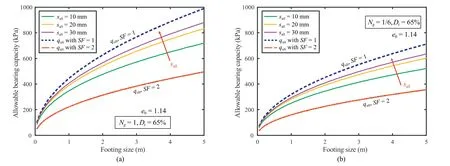
Fig.16.Allowable bearing capacity with variation of footing size:(a) Ng=1;and (b) Ng=1/6.

Fig.13 provides the predictions of qult,qband qcfor tests with both Ng=1/6 and Ng=1.The growth of footing ultimate bearing capacity and footing pressure with footing size is shown in Fig.13a for tests in soil of Dr=65% (e0=1.14).The footing pressure at a settlement of 0.1B is typically taken as the critical value of bearing capacity (e.g.the design method in the French standards (Cerato and Lutenegger,2007)).The cone penetration resistance is much smaller at the same depth of 0.1B,while the value of qcat 0.5B is found to be comparable and slightly larger than qultand qbat 0.1B.Specifically,the variations of qb/qcat 0.1B with footing size,relative density and gravity field are presented in Fig.13b.The ratio shows an increase with the relative density and gravity field,whereas the footing size effect is indistinctive.It is suggested that the critical value of bearing capacity for footings with various sizes could be easily estimated based on the measurement of cone penetration resistance at a certain depth for a given relative density and gravity field.

The bearing capacity of surface footing is largely dependent on the subsurface material,especially the soil in the vicinity of the footing.As illustrated in the footing scale effects,larger footing carries higher pressure on the soil,and the influence zone below the footing is therefore larger.The evaluation of influence zone can provide clues for the prediction of bearing capacity.With the CPTbased method,the size of influence zone,Zinf,could then be defined as the depth where the penetration resistance and the bearing capacity are equivalent(i.e.qult=qcat Zinf).Combining Eqs.(4)and(7) gives the expression of Zinfas follows:

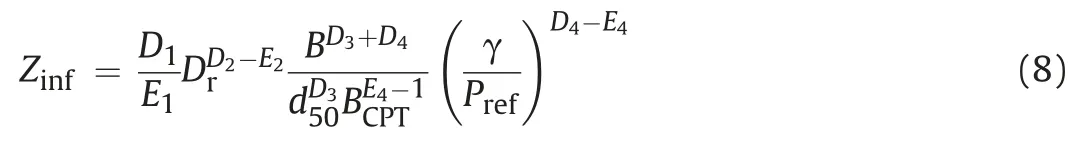
Fig.14 shows the variations of normalised influence zone with footing size,relative density and gravity field.It is clearly noted that the normalised influence zone increases with the relative density and decreases with the footing size.The magnitude of Zinf/B for the soil with higher relative density is reasonably larger.It should also be noted that the effect of gravity is not negligible.Higher g-level could increase the influence zone,and the magnitude for g/6 tests is about 83% of that for 1g tests.

6.Footing size effect and gravity effect

The bearing capacity of shallow spread footing is known to increase with footing size,whereas the phenomenon of nonlinear increase is attributed to the scale effect.Power function relations between footing size B and qultare proposed as qult∝Bβ,where β is the exponent indicating the nonlinear behaviour of footing size effect.From the evaluation of ultimate bearing capacity of circular footings(Eq.(4)),the footing size effect is quantitatively described by the magnitude of β=D3+D4=0.681.As the bearing capacity factor is only related to soil friction angle in the conventional prediction method,the value of β is normally assumed as 1.According to the Architectural Institute of Japan (AIJ,2001),β is suggested to be determined from experiments,and 0.67 is also recommended in practice(Nguyen et al.,2016),while β=0.69 was reported by Zhu et al.(2001) based on centrifuge tests and numerical analysis.By comparing model-scale footing tests and prototype foundation tests,‘engineering practice’modification of bearing capacity factor shows the value of β=0.8 by Shiraishi(1990),which is comparable to that obtained in this study.However,finite element simulation using a two-surface constitutive model noted the value of β close to 0.6,in consideration of non-associated flow,strain-softening and anisotropy,as reported by Loukidis and Salgado(2011).The studies suggest that the exponent index varies between 0.6 and 0.7,and the footing size effect is also dependent on other soil parameters,presumably including soil dilatancy and compressibility.

The gravity effects on foundation stiffness and ultimate bearing capacity are illustrated by the fitting parameters C4=0.168 and D4=0.184,respectively.Compared with the effects of relative density and footing size,the increases of kiand qultare much smaller,but not negligible.For example,the ultimate bearing capacity of surface circular footing on the Moon is approximately 72%（=）that of the same footing on the Earth,while the reduction ratio on the Mars is about 84%.In consideration of gravity effects on the Moon and Earth,the variations of ultimate bearing capacity with footing size and relative density are presented in Fig.15.Compared with available data from the lunar missions,data in squares are provided for an astronaut standing on one boot,for an Apollo Lunar Roving Vehicle wheel,and for the footpads of the robotic Surveyor spacecraft and the manned Lunar Module (after Heiken et al.,1991).The applied stress is to some extent less than the estimated ultimate bearing capacity for moderately dense sand that also corresponds to the average relative density of 65%for the top 15 cm of lunar soil.Data in grey area showing slightly higher bearing capacity were predicted using the conventional bearing capacity calculation method with estimated in situ soil density(ρ=1.5 g/cm3,and Dr≈65%)and strength parameters(cohesion of 0.1-1 kPa,and friction angle of 30°-50°)(after Mitchell et al.,1972;Durgunoglu and Mitchell,1975;Heiken et al.,1991),in which the gravity effect on the bearing capacity factor was not included.The overestimated predictions of bearing capacity were largely attributed to the failure mechanism of static CPTs proposed in Mitchell et al.(1972).The effects of surcharge and unit weight of soil were combined for convenience,and the failure zone extended above the end of foundation.Therefore,the predictions for penetration at relatively large depth overestimated the bearing capacity of shallow foundation.The results in Fig.15 show that cautions should be taken for foundations on soil with relative density Dr<50%(e0>1.3),although the bearing capacity is likely underestimated,and the predictions of this study could still contribute to the design of shallow foundations on the Moon and Mars.

In terms of the stability of foundations,geotechnical engineers tend to apply a safety factor (SF) or set a tolerance settlement sallto obtain the allowable bearing capacity qallin design,which can be calculated from the predictions using Eqs.(2)-(4) and expressed as

The variations of allowable bearing capacity with settlement are shown in Fig.16,as well as the gravity effect.For a given settlement,the allowable bearing capacity increases with footing size,but in a more gradual rate compared with the ultimate bearing capacity.More strict settlement control criteria could lead to a smaller value of qall.The analyses also include the predictions of bearing capacity with regard to a specified SF in design based on qult.When a higher SF is applied for foundation design,larger footing size is required to gain the allowable bearing capacity.The dependence of bearing capacity on the footing size,gravity,and design criteria has provided new understandings on the bearing capacity of shallow foundations under low gravity fields.

7.Conclusions

Low gravity effect on the bearing capacity of surface circular footings on a crushable granular material has been investigated in this study using a novel physical modelling approach involving magnetic force.In order to simulate accurate and stable low gravity fields,the GMMT method was adopted to realise saturated magnetisation and provide magnetic force counterweighting part of the Earth gravity acceleration.After curing the mixture of cement and iron oxide powder,a type of crushable magnetic planetary regolith simulant was prepared using hammer breaking method for angular particles.Despite the relatively low particle strength,the particle size distribution,particle shape and values of specific gravity and void ratio are comparable to those of lunar soil,representing immature agglutinates with vesicles.

Circular spread footings with various sizes were manufactured and pushed vertically into the granular material to obtain the loadsettlement response.The hyperbolic asymptote method was then used to evaluate both foundation stiffness and ultimate bearing capacity,and curve fitting parameters were provided for the estimations in consideration of relative density,footing size and gravity.Experimental results show that the load-settlement responses of shallow foundations under various low gravity fields can be generally predicted using the multivariate nonlinear regression for soil with Dr=60%-70%.Gravity field has shown its significant nonlinear relations with foundation stiffness and ultimate bearing capacity,whereas relative density affecting soil compressibility and shear strength seems to have more important effect on the mobilised friction angle.

To avoid uncertainties of soil property estimations,the CPTbased prediction of bearing capacity was proposed through the correlations between ultimate bearing capacity of shallow foundation and shallow penetration stiffness of CPT.Following the CPTbased method,the concept of influence zone below shallow foundation was adopted for the quantitative analysis,and the influence zone with variation of relative density and gravity has potential implications to the analysis of shallow foundation in both terrestrial and extraterrestrial geotechnical engineering.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors wish to thank the support from the ‘Double Tops’Construction Independent Innovation Project of China University of Mining and Technology (Grant No.2018ZZCX04).Experimental assistance from Jun Chen and Kang Yan is greatly appreciated.

List of symbols

B Width of foundation

BCPTDiameter of miniature penetrometer

c Cohesion

C1, C2, C3, C4Fitting parameters for foundation stiffness

d50Mean particle size

DrRelative density

D1, D2, D3, D4Fitting parameters for ultimate bearing capacity

e Void ratio

E1, E2, E3Fitting parameters for CPT stiffness

G Shear modulus

GsSpecific gravity

g Earth gravity

gmModelling gravity

I1, I2Magnetising current and magnetic force current

kiFoundation stiffness

ki,CPTCPT stiffness

Nc, Nq, NγBearing capacity factors

Ngg-level or acceleration factor

PrefAtmospheric pressure

q Surcharge

qallAllowable bearing capacity

qbFooting pressure

qcCone tip resistance

qultUltimate bearing capacity

s Footing settlement

sallallowable settlement

sγ Shape factor

z Penetration depth

ZinfFooting influence zone

β Exponent of footing size effect

γ Unit weight

σfParticle mean tensile strength

φ Mobilised friction angle

ρwWater density

ν Poisson’s ratio