A simplified three-dimensional extension of Hoek-Brown strength criterion

Hngzhou Li,Tong Guo,Ylin Nn,Bo Hn

a Department of Civil Engineering,Xi’an Jiaotong University,Xi’an,Shaanxi,710049,China

b Shaanxi Engineering Research Center of Soil Body,China Electronic Research Institute of Engineering Investigation and Design,Xi’an,Shaanxi,710054,China

Keywords:Hoek-Brown (HB) strength criterion Three-dimensional (3D) strength criterion Intermediate principal stress Failure envelope

ABSTRACT The Hoek-Brown (HB) strength criterion has been applied widely in a large number of projects around the world.However,this criterion ignores the intermediate principal stress σ2.Many evidences have demonstrated that the rock strength is dependent on σ2.Thus it is necessary to extend the HB criterion into a three-dimensional(3D)form.In this study,the effect of σ2 on the strength of rocks is identified by reviewing the true triaxial tests of various rock types reported in the literature.A simple 3D strength criterion is developed.The modified criterion is verified by the true triaxial tests of 13 rock types.The results indicate that the modified criterion can achieve a good fit to most of rock types.It can represent a series of criteria as b varies.For comparisons,several existing 3D versions of the HB criterion are selected to predict the strengths of these rock types.It is indicated that the proposed criterion works better than other criteria.A substantial relationship between parameter b and the unconfined compressive strength is established,which guarantees that the proposed criterion can still work well even in the absence of true triaxial test data.

1.Introduction

Many strength criteria have been proposed to describe rock failure in the past decades.Among these strength criteria,the Hoek-Brown(HB)strength criterion developed by Hoek and Brown(1980) and Hoek et al.(2002) has been applied widely in rock mechanics and rock engineering.This criterion incorporates intact rock and discontinuities into a system designed to estimate the mechanical behavior of typical rock masses encountered in rock engineering practices (Hoek and Brown,2019).Its parameters can be determined from uniaxial compression test,mineralogical examination and characterization of rock discontinuities.The HB criterion has undergone a series of developments which are summarized in Hoek and Marinos (2007).Hoek and Brown (2019)further discussed some issues of the criterion related to input data and practical applications.

However,the HB criterion ignores the intermediate principal stress σ2.Many evidences have illustrated that the strength of rocks is dependent upon σ2.Murrell(1965)presented the influence of σ2by comparing the results of triaxial compression and extension tests conducted on Darley Dale sandstone.Mogi (1967,1971a,b,2007)observed that σ2has a significant effect on the strength based on the true triaxial test of rock samples from a variety of lithology,and proposed several three-dimensional (3D) strength criteria to simulate the effect of σ2.Chang and Haimson(2000),Haimson and Chang(2000),Haimson and Rudnicki(2010)and Ma and Haimson(2016)conducted an extensive series of tests on several rock types and their results indicated that σ2has different effects on strength and failure mode for different rock types.Similar test results were also reported by other researchers(e.g.Takahashi and Koide,1989;Sriapai et al.,2013;Feng et al.,2016).

These evidences have provoked the attention of considering the effect of σ2in strength criteria.Colmenares and Zoback(2002),Al-Ajmi and Zimmerman (2005) and Benz and Schwab (2008)compared several criteria by fitting the published polyaxial data,and found that the criteria considering σ2could fit these polyaxial data better than those neglecting σ2for most of rocks.A number of 3D versions of the HB criteria have been developed by researchers.Pan and Hudson(1988)developed a 3D HB criterion based on the original HB criterion and the failure envelope is circular in π plane,and this criterion cannot reduce to the original HB criterion.Singh et al.(1998) obtained a 3D version of the HB criterion by substituting the mean of σ2and the minor principal stress σ3for σ3.Priest (2005) developed a comprehensive 3D HB criterion by giving a circumscribed fit for the HB criterion with the Drucker-Prager criterion and a simplified criterion by introducing an intermediate principal stress weighting factor,respectively.The two 3D criteria were compared to other 3D criteria by Priest (2010,2012).For the comprehensive Priest criterion,Melkoumian et al.(2009) presented an explicit solution combined with numerical stress modeling codes.Zhang and Zhu (2007) modified the original HB criterion into 3D form by using a general form of rock strength criterion proposed by Mogi (1971b),which is similar to that of Pan and Hudson (1988).Based on the generalized twodimensional (2D) HB criterion,Zhang (2008) extended the Zhang-Zhu criterion into a generalized 3D form.Zhang et al.(2013) continued to utilize three different Lode dependences to solve the non-smoothness and non-convexity of this 3D criterion.Benz et al.(2008)enhanced the original HB criterion by adopting the spatially mobilized plane concept.Jiang et al.(2011),Jiang and Xie(2012),Lee et al.(2012),Jiang and Zhao(2015),Jiang(2017a,b)and Wu et al.(2018) developed several 3D versions of the HB criterion by introducing different deviatoric shape functions into the stress invariant form of the HB criterion.

The methods for generalizing the HB criterion into a 3D form can be classified into three categories:(i) introducing a deviatoric shape function g(θσ)into the HB criterion,e.g.Jiang et al.(2011),Lee et al.(2012),Zhang et al.(2013),Jiang and Xie (2012),Jiang and Zhao (2015),Jiang (2017a,b);(ii) combining the HB criterion with other 3D criteria,e.g.Priest (2005) (the comprehensive Priest criterion),and Zhang and Zhu (2007);and (iii) introducing a weight combination of σ2and σ3,e.g.Singh et al.(1998),and Priest(2005)(the simplified Priest criterion).Most of the 3D HB criteria inherit the characteristics of the HB criterion.All of them can reflect the influence of σ2to some extent,which has been validated by the researchers.It is important to note that the criteria obtained from Methods i and ii are expressed in terms of the stress invariant which brings the computational inconvenience,and the criteria obtained from Method iii belong to a monotonically increasing function.

Due to the complexity of rock strength,there are some arguments on the adequacy of σ2dependence on strength for some rocks.Chang and Haimson (2005)presented that the Long Valley Caldera rock hardly exhibits any meaning of σ2.Chang and Haimson (2005) pointed out that the Mohr-Coulomb and HB criteria fit the rocks that are hardly dependent on σ2equally well,or even better than 3D failure criteria.All the evidences show that the σ2effect is complicated for rocks.Different rock types maybe show different σ2dependence characteristics.Accurate prediction of rock strength in a polyaxial stress state is a great challenge to a 3D strength criterion.Over hundreds of strength criteria have been developed,but a universal strength criterion which is able to describe the behavior of various materials under complex stress state does not exist.Thus it is necessary to develop a 3D criterion which can describe the strength characteristics of various rock types as much as possible.

The objective of the article is to develop a simplified and versatile 3D HB criterion.An intermediate principal stress coefficient is introduced into the HB criterion by reviewing the σ2effect on the strength of selected rock types.The new 3D HB criterion is expected to work well for various rock types and compared with other existing 3D versions of the HB criterion.The generalization of the 3D HB criterion is briefly examined in the absence of true triaxial test data when only uniaxial and triaxial tests are available.

2.Extension of HB strength criterion

2.1.HB strength criterion

The HB strength criterion was originally developed by Hoek and Brown (1980) and has undergone several revisions.The recent version is the generalized HB failure criterion (Hoek et al.,2002;Hoek and Brown,2019).The HB criterion and the associated geological strength index (GSI) have been widely accepted to estimate the strength characteristics of intact rocks and jointed rock masses.It is expressed as

where σ1is the major principal stress;σcis the unconfined compressive strength(UCS)for intact rock;and mb,s and α are the rock mass material constants estimated from the GSI,given by

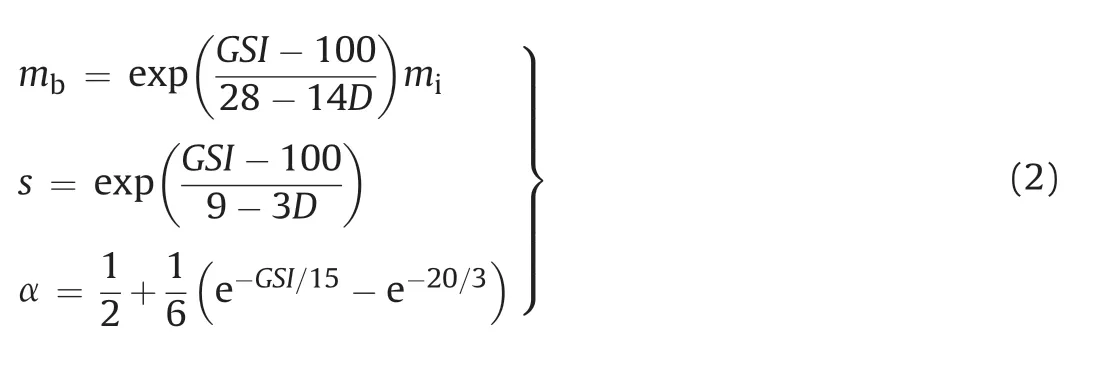
where miis the material constant for intact rock,and D is the disturbance factor which varies from 0 for undisturbed in situ rock masses to 1 for very disturbed rock masses.Eq.(1) reduces to the original HB criterion for the intact rock as s=1 and α=0.5.

The HB failure criterion cannot provide good prediction for rocks in polyaxial stress state due to the ignorance of σ2.Therefore,it is necessary to generalize the HB criterion from the triaxial stress state to 3D stress state.

2.2.Strength characteristics of rocks in 3D stress state

Fig.1 shows the results of the true triaxial compression test on a typical rock type,i.e.the Coconino sandstone (Ma and Haimson,2016).One can see from this figure that the rock strength is significantly dependent on σ2ranging from σ3to σ1.For a constant σ3,the rock strength increases with the rise in σ2until it reaches a peak value,and then gradually decreases with the further increase of σ2.Finally,it almost approaches its initial magnitude at σ2=σ3.Similarly,the effect of σ2on the rock strength was observed on Bentheim sandstone,Linghai granite,Chelungpu siltstone by Ma and Haimson(2016),Haimson and Rudnicki(2010) and Feng et al.(2016),respectively.

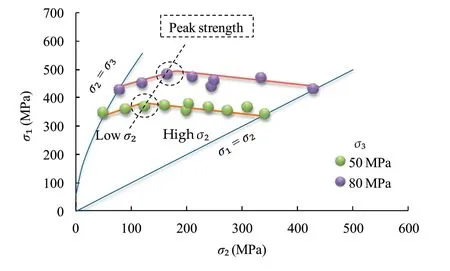
Fig.1.Influence of σ2 on strength of Coconino sandstone (test data derived from Ma and Haimson,2016).

Mogi (1967,1971a,b,2007),Takahashi and Koide (1989) and Chang and Haimson (2000) conducted extensive true triaxial compression tests on various rock types,including the Dunham dolomite,Mizhho trachyte,Manazuru andesite,Solenhofen limestone,Yamaguchi marble(Mogi,1967;1971a;b,2007);Shirahama sandstone,Izumi sandstone,Horonai sandstone,and Yuubari shale(Takahashi and Koide,1989);and KTB amphibolite (Chang and Haimson,2000).In spite of the insufficient true triaxial data at high σ2approaching σ1,all the tests have confirmed that the effect of σ2on rock strength has the characteristics similar to that indicated in Fig.1.Xu and Geng(1985)complemented the true triaxial test of Yamaguchi marble done by Mogi (1971a,b) at high σ2approaching σ1,and the above effect of σ2on rock strength is further confirmed.All collected evidences show that the rock strength has a substantial trend toward an eventual decrease at high σ2when σ3is held constant.Note that the rock strength is always equal to or higher than that in the triaxial compression state(σ2=σ3).

2.3.Mechanism of σ2 effect on rock strength

For a given σ3,the effect of σ2can be divided into two parts to illustrate the trend:low σ2range and high σ2range,as shown in Fig.1.In the low σ2range,the rock strength increases with the increase of σ2,while the strength decreases in the high σ2range,as shown in Fig.1.Thus,the effect of σ2on rock strength should be identified in order to generalize the HB criterion into an appropriate simple 3D version.

The mechanism of the σ2effect on rock strength is complicated.The rocks are heterogeneous and have many microcracks in nature,which is an important factor to be considered when the mechanism of σ2effect is investigated.Cai(2008)and Pan et al.(2012)indicated that the material heterogeneity plays a major role in the failure of rocks under the effect of σ2.The failure of rocks is a complex process involving microcrack initiation,propagation and calescence.Thus,the effect of σ2on rock behaivor should be focused on the stressinduced anisotropic strength and deformation behaviors of the rocks.Chang and Haimson(2000,2005)found that the effect of σ2depends on the dilation,crack initiation and propagation by comparing the results of the true triaxial tests and scanning electron microscopy(SEM)tests on different rocks.The true triaxial test conducted by Feng et al.(2016)also showed that the effect of σ2is related to the volumetric strain.Cai (2008) presented that the stress-induced fractures depend on rock stress and strength conditions as well as the material heterogeneity.The existence of σ2alters the rock fracturing process in a way that the cracks initiate and propagate in a preferred direction.Most of the cracks formed in the rocks are different under different magnitudes of σ2.

It is considered that σ2plays two roles simultaneously in rock deformation:one is to restrict the deformation development,and the other is to promote the development of fractures and accelerate the failure.The σ2mainly restrains the deformation in the σ1direction and delays the onset of the local failure when σ2is low(Cai,2008;Pan et al.,2012),which is also illustrated experimentally by Feng et al.(2016).In this case,further stress in the σ1direction should be applied,which leads to a higher rock strength when σ2is not sufficiently large.On the other hand,the internal elements of rocks can fail during the process of applying σ2,as illustrated by Pan et al.(2012).If σ2is high enough,too many internal elements of rocks would fail due to the effect of σ2,which involves the crack initiation,propagation and calescence.In this case,σ2would accelerate the rock failure and there is no need for a high σ1to induce the rock failure,which means that σ2reduces the rock strength.

Thus,the mechanism of σ2effect on rock strength is clearly identified based on these evidences,which is the reason that the effect of σ2can be divided into two parts,as illustrated in Fig.1.When σ2is low,the effect of σ2is mainly to restrain the rock failure and increase the rock strength as that of σ3,whereas high σ2values lead to an inverse effect and induce the rock failure as the effect of σ1.

2.4.A 3D version of HB criterion

Most of the existing 3D versions of the HB criterion are expressed in terms of the stress invariants,and a recursive numerical strategy should be applied to determining the rock strength.Singh et al.(1998) obtained a simple 3D HB failure criterion by substituting the average of σ3and σ2for σ3,which overestimates the role of σ2in rock strength.Priest(2005)assumed that the value of σ3in the comprehensive Priest criterion was weighted by the specified σ2and σ3.Hence,σ3can be replaced by ωσ2+（1 -ω）σ3,where ω is a weighting factor in the range of 0-1.Priest(2005) found that the value of ω can be adjusted to provide the best-fit for the strength of rocks.As illustrated above,the effect of σ2would not always increase the rock strength,but almost all the rock types have the trend of strength reduction above a critical level of σ2.However,the simple versions of the HB criterion(Singh et al.,1998;Priest,2005)belong to a monotonically function of σ2,which conflicts this trend.

According to the mechanism of σ2effect as explained above,σ2plays two roles,i.e.restricting the deformation development and promoting fracture development.The positive effect of σ2on rock strength is more significant than the opposite effect at low σ2values and vice versa.In this case,it can be considered that the effect of σ2is the same as that of σ3to improve the rock strength at low σ2values,and assumed that the weighted average of σ2and σ3,i.e.（bσ2+σ3）/（1 +b）,increases the rock strength as σ3does,in which b is defined as an intermediate principal stress coefficient to evaluate the effect of σ2.When the value of σ2is large,the effect of σ2is to induce the rock failure as σ1does.The weighted average of σ1and σ2,i.e.（σ1+bσ2）/（1 +b）,is adopted to accelerate the rock failure,which reduces the strength of rocks.Based on the above assumption,the effect of σ2is approximated through linear interpolation with σ1and σ3,respectively.Then σ2can be introduced reasonably to extend the HB criterion (Eq.(1)) into 3D form.

Thus,to consider the effect of σ2on the rock strength in the HB criterion,σ3in Eq.(1)can be replaced by the weighted average of σ2and σ3,i.e.（bσ2+σ3）/（b+1）,in the low σ2range.In the high σ2range,σ1in Eq.(1)should be replaced by the weighted average of σ1and σ2,i.e.（σ1+bσ2）/（b+1）.A 3D version of the HB criterion is then developed and expressed as

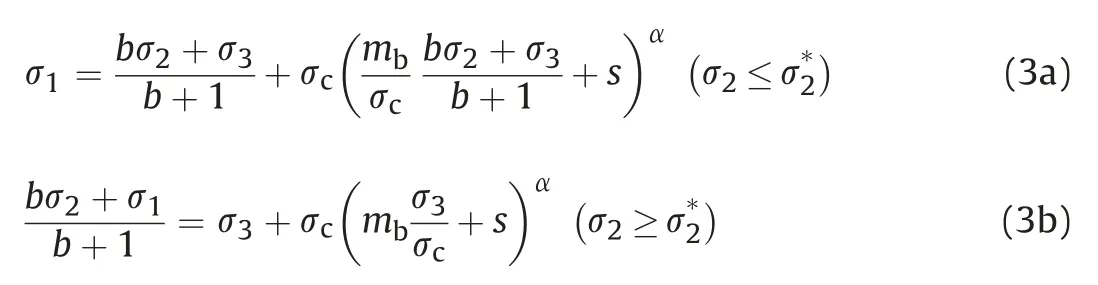
Generally,the effect of σ2is lower than that of σ1and σ3(Mogi,2007),thus b takes the values of 0-1.The peak strength in σ1-σ2space for a constant σ3level occurs at σ2=σ*2,which is the intersection of Eqs.(3a)and(3b).σ*2can be determined as Eqs.(3a)and(3b)are equal.Herein,the formula of σ*2is not presented due to the complexity of the mathematical expression which can be obtained easily using Matlab’s built-in function Solve.There is an additional simple way to decide which equation (Eq.(3a) or (3b)) should be used for a specific situation irrespective of,in which the lower σ1calculated from Eqs.(3a) and (3b) is adopted as the strength of rocks.Zhang et al.(2020)argued that the role that σ2plays could be accounted for by a completing process between the mean stress effect and the Lode angle effect,which hypothesizes that the rock strength increases with σ2if the mean stress strengthening effect surpasses the Lode angle weakening effect,otherwise the rock strength decreases.Therefore,the meaning of b can be clarified further from the view of Zhang et al.(2020).The mean stress effect and the Lode angle effect can be reflected from the failure envelopes in the deviatoric plane and meridian plane intuitively.The failure envelope of the new criterion varies with different b values,as shown in Fig.2.Therefore,b can also be regarded as a shape factor of failure envelope,which controls the shape of failure envelope,i.e.Lode dependence function.

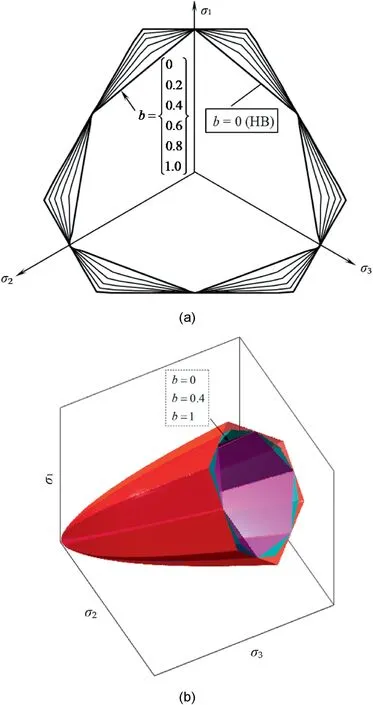
Fig.2.Failure envelopes of the proposed 3D HB criterion in(a)π plane and(b)the 3D principal stress space.

Fig.3.Effect of b on the rock strength(test data derived from Ma and Haimson,2016).

The proposed criterion has a simple mathematical expression.It inherits the merits of the original HB criterion.Compared with other existing 3D HB criteria in terms of the stress invariant which brings the computational inconvenience,the new criterion can obtain an analytical solution of the strength easily.Fig.2 shows the failure envelopes of the proposed criterion with different b values in π plane and in the 3D principal stress space,respectively.Furthermore,it can represent a series of strength criteria when b takes different values,which is convenient to predict the strengths of various rock types.Failure envelopes increase with the increase of b.When b=0,the strength criterion (Eq.(3a) and (3b)) reduces to the HB strength criterion(Eq.(1)).Note that the proposed criterion predicts the same strength as the original HB criterion at the conventional triaxial compression (σ2=σ3) and extension (σ1=σ2) stress states irrespective of b,as shown in Fig.3.In addition,the failure envelope of the criterion is non-smooth which causes inconvenience in numerical simulation.If the proposed criterion is used for plastic analysis,the corners do not have a unique gradient for defining the direction of the inelastic deformation(Borja,2013;Labuz et al.,2018).Several methods have been developed to handle corners of the strength criteria (Sloan and Booker,1986;Runesson et al.,1988;Yu et al.,2005),which can be applied to the proposed criterion.

Fig.3 shows the strength calculated using Eqs.(3a) and (3b)with different b values.The HB criterion,i.e.b=0,underestimates the rock strength due to the ignorance of σ2,which has a horizontal fitting line.The proposed criterion with b=1 is the upper bound of the strength for most of rocks.The best-fit of the rock strength lies in the range of b=0 to b=1.

The proposed criterion has the same parameters as that of the HB criterion(Eq.(1))except for b.The parameters GSI,s,α,σcand miare determined as the HB criterion does.From Eqs.(3a)and(3b),a system of equations can be constructed using test data associated with σ1,σ2and σ3,and then b can be obtained using the least-square method which can be realized easily using Microsoft Excel’s builtin optimization routine Solver.In this case,the value of b is determined using the true triaxial test data which is difficult to be performed.Fortunately,we found that b and σcremain a substantial relationship,and b can be determined from σc,which will be discussed in Section 5.

3.Calibration and validation

The results of the true triaxial tests on 13 rock types are collected to verify the proposed strength criterion.These rock types include the Dunham dolomite,Mizhho trachyte,Manazuru andesite,Solenhofen limestone,Orikabe monzonite,Yamaguchi marble(Mogi,1967,1971a,b,2007);Shirahama sandstone,Yuubari shale(Takahashi and Koide,1989);Westerly granite(Haimson and Chang,2000);KTB amphibolite (Chang and Haimson,2000);siltstone drilled from Chelungpu fault in Cores I and II (Haimson and Rudnicki,2010);and Coconino sandstone(Ma and Haimson,2016).

All the rock types are considered to be isotropic and intact.Thus the material parameters GSI,s and α are equal to 100,1 and 0.5,respectively.Parameters σcand mican be determined from the uniaxial and triaxial compression tests.Wu et al.(2018) summarized five methods for determining the parameters σcand mi.Although the same rock types are used,the values of miand σcdetermined using different methods have some differences(Colmenares and Zoback,2002;Priest,2005;Zhang and Zhu,2007;Jiang and Xie,2012;Jiang,2017a),which can bring different prediction results (Jiang,2017a).For eliminating the differences of these material parameters,miand σctake the same values as that of the HB criterion (Eq.(1)).σcadopts the result of the uniaxial compression test directly,miis determined from the triaxial compression tests,and b is obtained from the true triaxial test data using the least-square method.Table 1 lists the parameters σc,miand b for various rock types.Note that the UCS values of the Yuubari shale and Shirahama sandstone are unavailable due to the absence of the uniaxial compression test.σcvalues for these two rock types are approximated from the conventional triaxial compression tests.Figs.4-7 present the validation results of the proposed 3D HB criterion for each rock type.

Fig.4 shows that the true triaxial test data from σ2=σ3to σ2=σ1are almost complete,which can reflect the whole effect of σ2on rock strength.Fig.4a-c shows that the proposed criterion works well for Chelungpu siltstones I and II,and Coconino sandstone with b=0.464,0.268 and 0.215,respectively.The strengths of the three rock types at σ2=σ3and σ2=σ1are almost equal.Each rock type is corresponding to different b values which quantify the effect of σ2.The greater b value implies the stronger σ2dependence on strength.For the Mizhho trachyte in Fig.4d,the test data are somewhat scattered in the high σ2range.The triaxial strength in compression(σ2=σ3) is greater than that in tension (σ2=σ1).The proposed criterion predicts the strength well at the low σ2range,while it yields some misfits as predicting the decrease of the strength at the high σ2range.This is because the proposed criterion keeps the same strength at σ2=σ3and σ2=σ1.

Although the test data are insufficient in the range of high σ2approaching σ1,the effect of σ2as mentioned in above section still can be concluded,as shown in Figs.5 and 6.For the Solenhofen limestone,Shirahama sandstone,Yuubari shale,and KTB amphibolite as shown in Fig.5,the 3D HB criterion predicts the rock strength well with b=0.492,0.421,0.325 and 0.41,respectively.For the Dunham dolomite in Fig.6a,the criterion with b=0.606 predicts the strength well in the low σ2range.In thehigh σ2range,the criterion achieves a good prediction for the high constant σ3,while it underestimates the strength for the low constant σ3.The Yamaguchi marble and Manazuru andesite present an unusual behavior in the range of high σ2as the effect of σ2varies with σ3,as shown in Fig.6b and c.For the case,the criterion still can achieve a good fit with b=1 and 0.452,respectively,especially in the low σ2range.

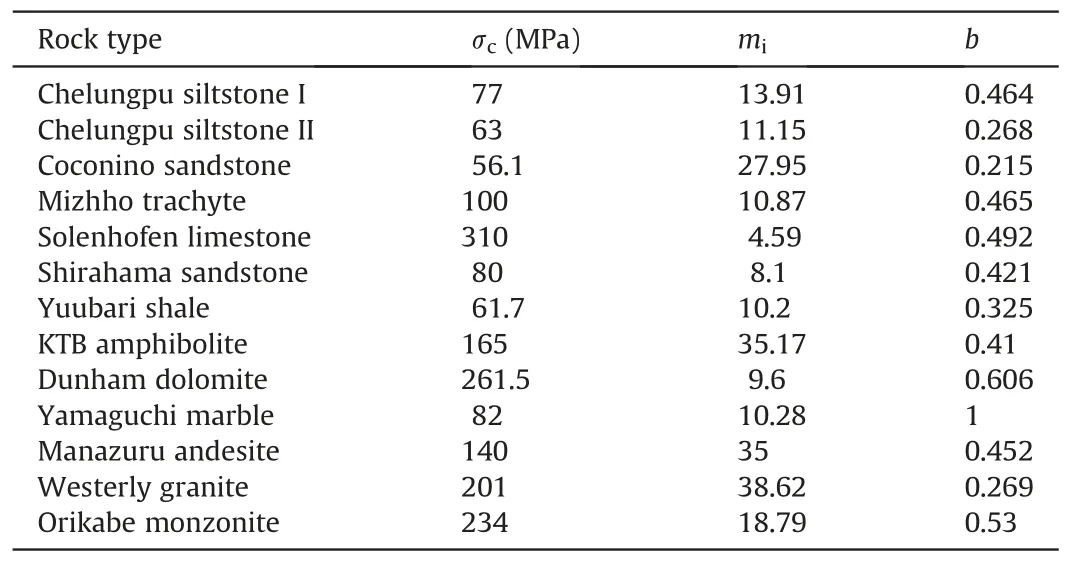
Table 1Parameters of the proposed 3D HB criterion for various rocks.

For the Westerly granite and Orikabe monzonite shown in Fig.7,the test data in the high σ2range are hardly available.The proposed criterion predicts the strength of the two rock types with b=0.269 and 0.53,respectively.In spite of the lack of test data at high σ2,the effect of σ2seems to be the same as that of other rock types and illustrated theoretically by the proposed criterion.

Overall,the proposed criterion can works well for all collected rocks,especially for the strength at low σ2.The effect of σ2on the rock strength can be quantified by an appropriate b value as illustrated in Fig.3.The greater b represents the stronger σ2dependence.Colmenares and Zoback (2002) defined a correlation coefficient to quantify the influence of σ2on the failure of five rocks including Dunham dolomite,Solenhofen limestone,KTB amphibolite,Yuubari shale and Shirahama sandstone,which is consistent with the effect of b.Note that the proposed criterion cannot depict the trend of σ2dependence well at lower confining pressure for some rocks.This is because the effect of σ2is dependent on σ3as illustrated by Priest (2005) and Xu et al.(2017).However,the parameter b reflects the magnitude of the σ2effect,but it is independent of σ3for a specific rock type.

Colmenares and Zoback (2002) presented that for some rock types (e.g.Shirahama sandstone and Yuubari shale),σ2hardly affects rock failure at some values of σ3and the Mohr-Coulomb and HB criteria fit these test data equally well as,or even better than,the more complicated polyaxial criteria.Herein,the comparison between the proposed criterion and the results of Colmenares and Zoback(2002)is conducted on the Yuubari shale.The parameters listed in Table 1 are used for the proposed criterion,which is different from those of Colmenares and Zoback(2002) who performed a grid search for all test data to find out the best-fitting parameters.The root mean squared error (RMSE)is used as an indicator of the misfit between the calculated strength and the test data.The RMSE is calculated as

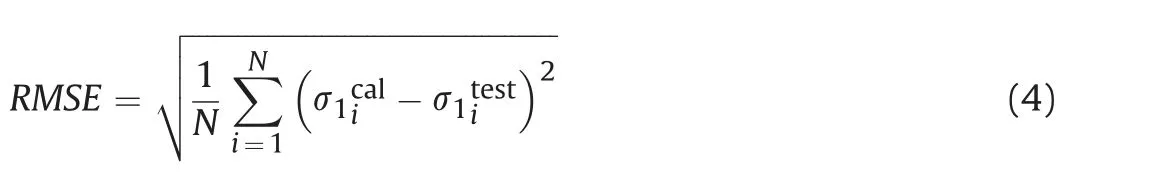
where N is the number of test data pairs;andare the ith calculated and measured values of σ1,respectively.The comparison results are shown in Fig.8.The misfits of the proposed criterion and Colmenares and Zoback (2002)’s results are 9.4 MPa and 12.9 MPa,respectively,indicating that the proposed criterion provides a better prediction.Comparatively,the criterion can reproduce the results of the test data,while the results in Colmenares and Zoback (2002) go through the middle of the test data for each σ3.It suggests that the proposed criterion can work better no matter how the effect of σ2is.

4.Comparison with other existing 3D HB criteria

4.1.Other existing 3D HB criteria

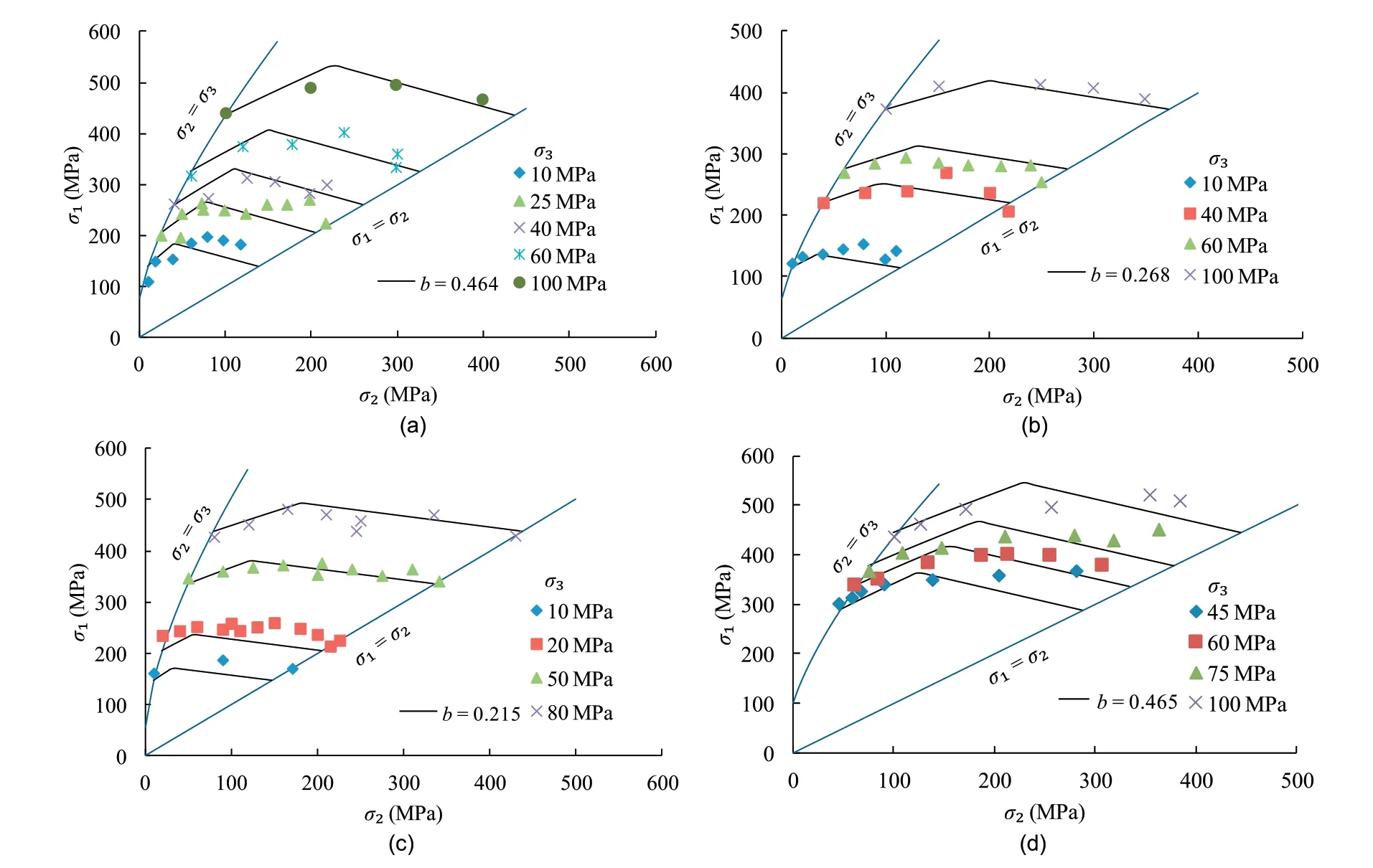
Fig.4.Validation of the proposed 3D HB criterion for (a) Chelungpu siltstone I,(b) Chelungpu siltstone II,(c) Coconino sandstone,and (d) Mizhho trachyte.

As mentioned in the Introduction,there have been a number of existing 3D HB criteria developed to describe the effect of σ2.In this section,the objective is to find out which failure criterion can evaluate the effect of σ2on strength best.For comparison,the criteria modified by Pan and Hudson (1988),Priest (2005),Zhang and Zhu (2007),Lee et al.(2012) and Jiang and Zhao (2015) are selected.Priest (2012) demonstrated that the simplified Priest criterion works better than the comprehensive one.Thus the simplified Priest criterion is selected.These selected criteria cover all three methods generalizing the HB criterion into a 3D version as summarized in the Induction,which can be expressed as follows:

Pan-Hudson criterion (Pan and Hudson,1988):

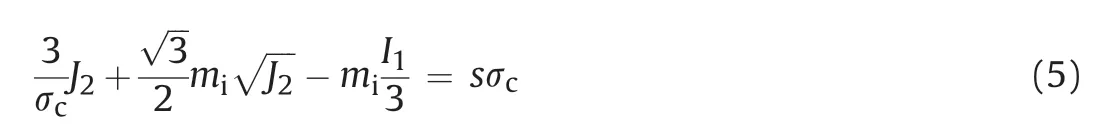
Simplified Priest criterion (Priest,2005):

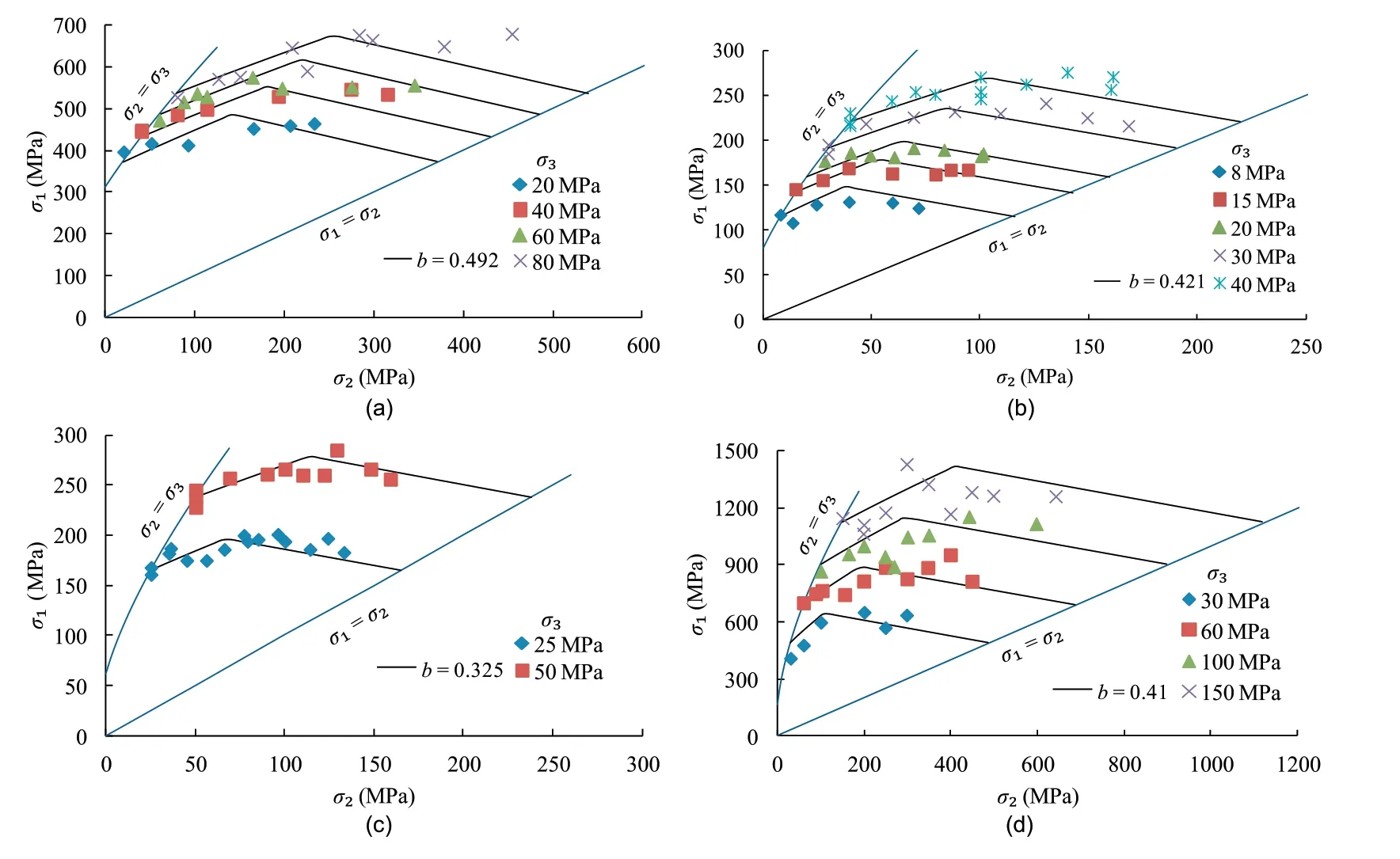
Fig.5.Validation of the proposed 3D HB criterion for (a) Solenhofen limestone,(b) Shirahama sandstone,(c) Yuubari shale,and (d) KTB amphibolite.

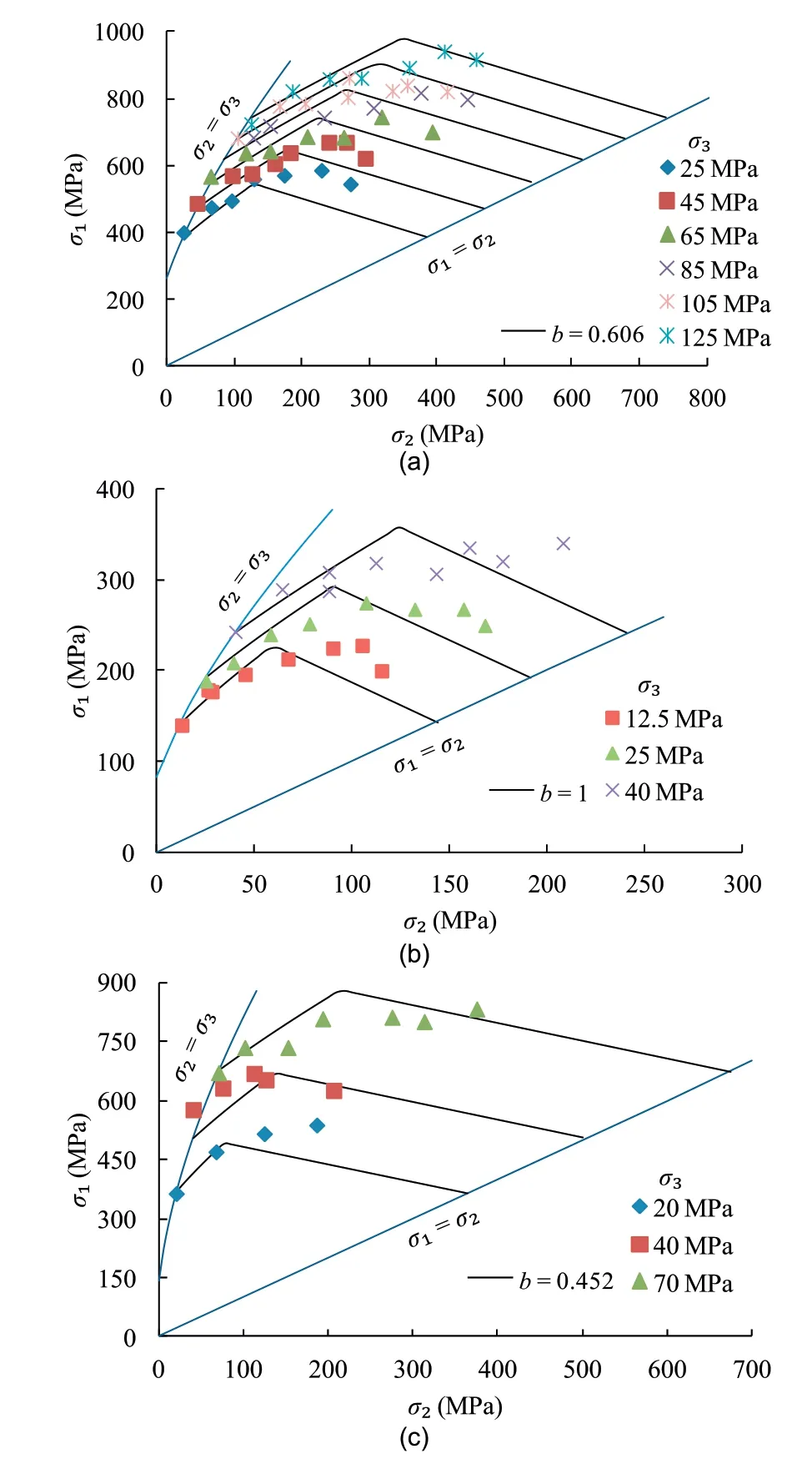
Fig.6.Validation of the proposed 3D HB criterion for (a) Dunham dolomite,(b)Yamaguchi marble,and (c) Manazuru andesite.

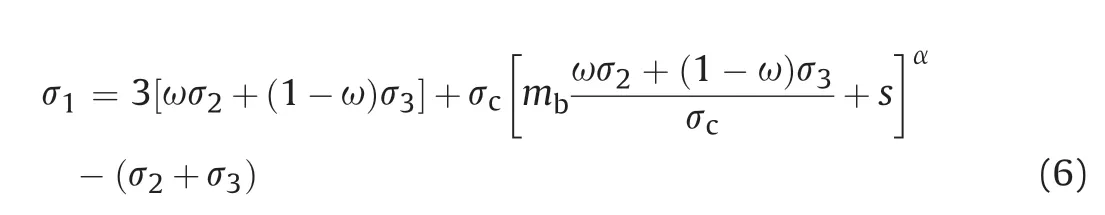
Zhang-Zhu criterion (Zhang and Zhu,2007):

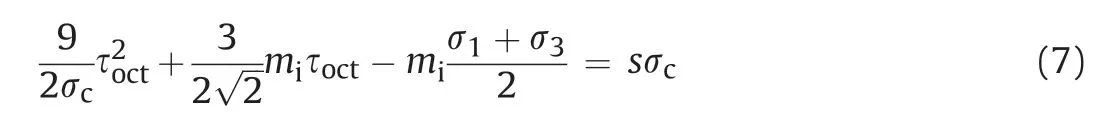
Jiang-Zhao criterion (Jiang and Zhao,2015):

Lee criterion (Lee et al.,2012):

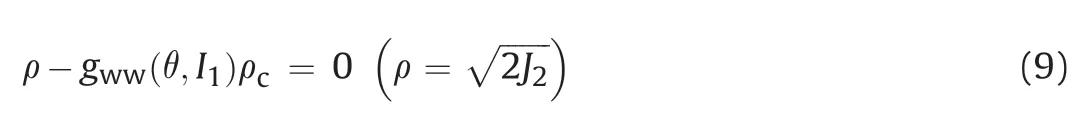
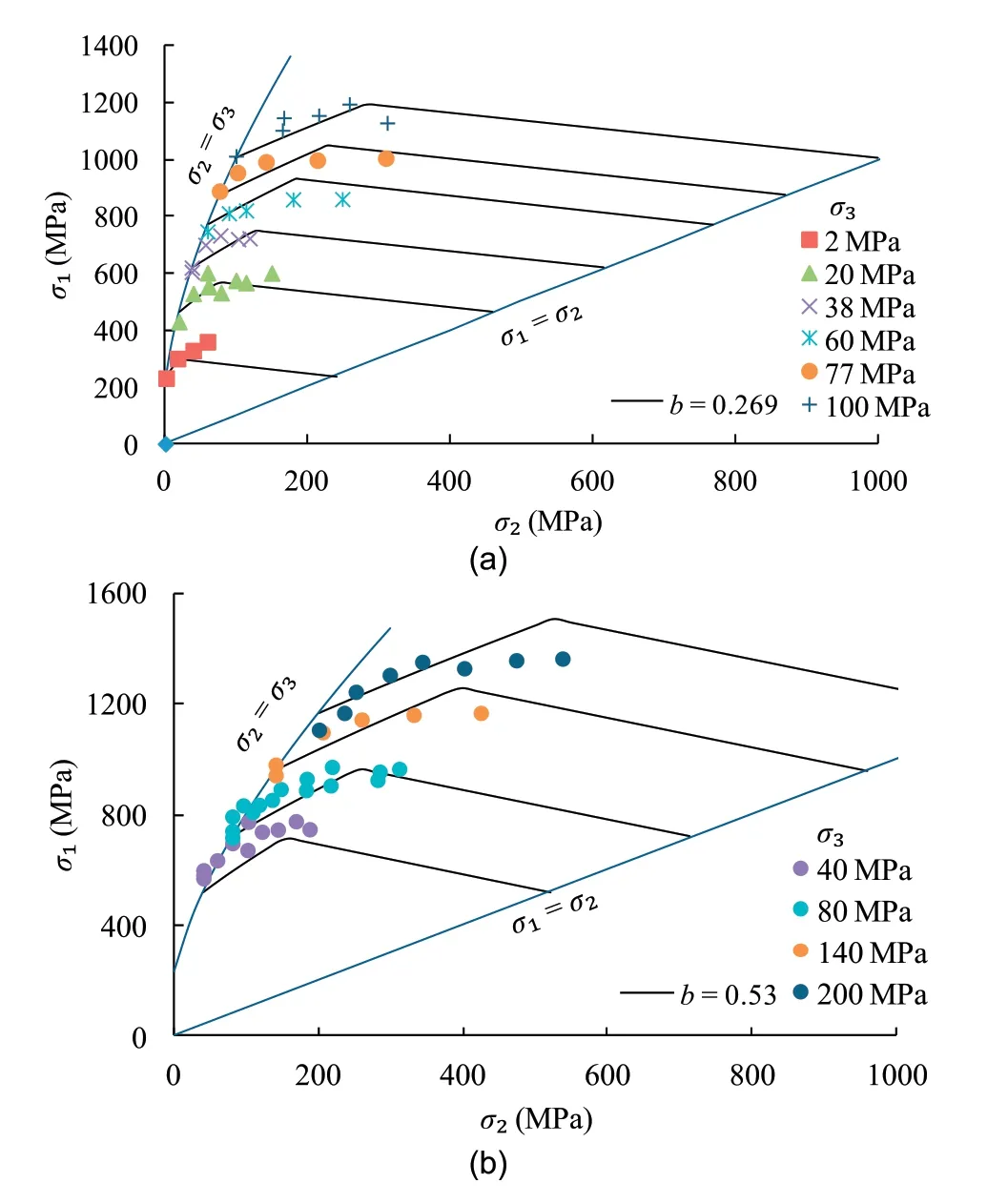
Fig.7.Validation of the proposed 3D HB criterion for (a) Westerly granite,and (b)Orikabe monzonite.

where I1is the first stress invariant,J2is the second deviatoric stress invariant,τoctis the octahedral shear stress,θ is the Lode angle(0°-60°),gww(θ,I1) is a shape function (Lee et al.,2012),and ρcrepresents the maximum value of ρ in the triaxial compression domain.These criteria,except for the simplified Priest criterion,need a recursive numerical strategy to calculate σ1,which causes computational inconvenience.

Fig.9 shows the failure envelopes of the selected criteria and the proposed criterion (with b=0 and 1) in π plane.The Zhang-Zhu,Lee and Jiang-Zhao criteria predict the same strength as the HB criterion at both the triaxial stress states of compression (σ2=σ3)and extension (σ1=σ2),as well as the proposed criterion.It is important to mention that the Zhang-Zhu criterion is a non-convex criterion,as shown in Fig.9.Compared with the HB criterion,the Pan-Hudson criterion underestimates the strength at σ2=σ3and overestimates the strength at σ1=σ2.The simplified Priest criterion has an additional parameter ω to reflect the effect of σ2.It predicts the same strength as the HB criterion at σ2=σ3,but not at σ1=σ2.

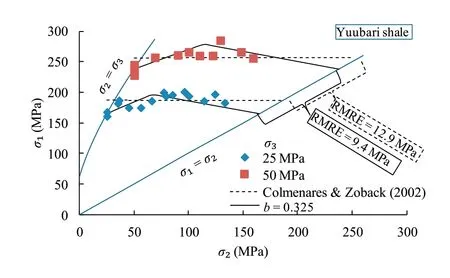
Fig.8.Comparison of the proposed 3D HB criterion with Colmenares and Zoback(2002)’s results.

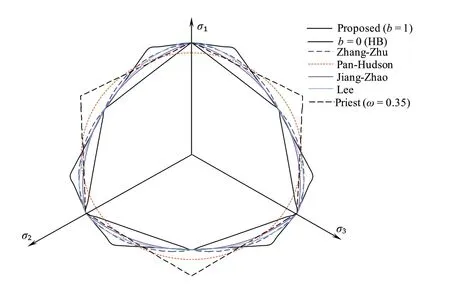
Fig.9.Failure envelopes of 3D HB criteria in π plane.

For comparison,σcand mblisted in Table 1 are adopted for all the criteria.The parameter ω in Table 2 is used for the Priest criterion(Eq.(6)),which is obtained by best-fitting to true triaxial test data.Note that unlike Priest (2005),the effect of σ3on ω is not considered.The RMSE is still used as the misfit to further evaluate the performance of these criteria.

4.2.Comparison results

The misfits of all criteria are shown in Fig.10.The proposed criterion works best for most of rock types,including the Chelungpu siltstones I and II,Coconino sandstone,Yamaguchi marble,Manazuru andesite and Orikabe monzonite.Even though the proposed criterion cannot yield the least misfits for Shirahama sandstone,Yuubari shale and Westerly granite,it still predicts the strengths of the three rock types relatively well,second only to the Lee criterion that fits these rocks as well as KTB amphibolite best,as shown in Fig.10.The simplified Priest criterion fits the Mizhho trachyte best.The Zhang-Zhu criterion predicts the Solenhofen limestone and Dunham dolomite best.The Jiang-Zhao criterion cannot work well for the Chelungpu siltstones I and II,and Yuubari shale,as shown in Fig.10,but it has almost the same misfits as the proposed criterion.The Pan-Hudson criterion works worst for all selected rock types except the Yamaguchi marble and Manazuru andesite.Note that in order to more clearly identify the differences of other 3D HB failure criteria,the results of Pan-Hudson criterion are not included in Figs.10 and 11 due to the much larger errors.Overall,the proposed criterion can work well for most of rocks,followed by the Lee criterion,Priest criterion,Jiang-Zhao criterion,Zhang-Zhu criterion and Pan-Hudson criterion.

Table 2Parameter ω for the Priest criterion.

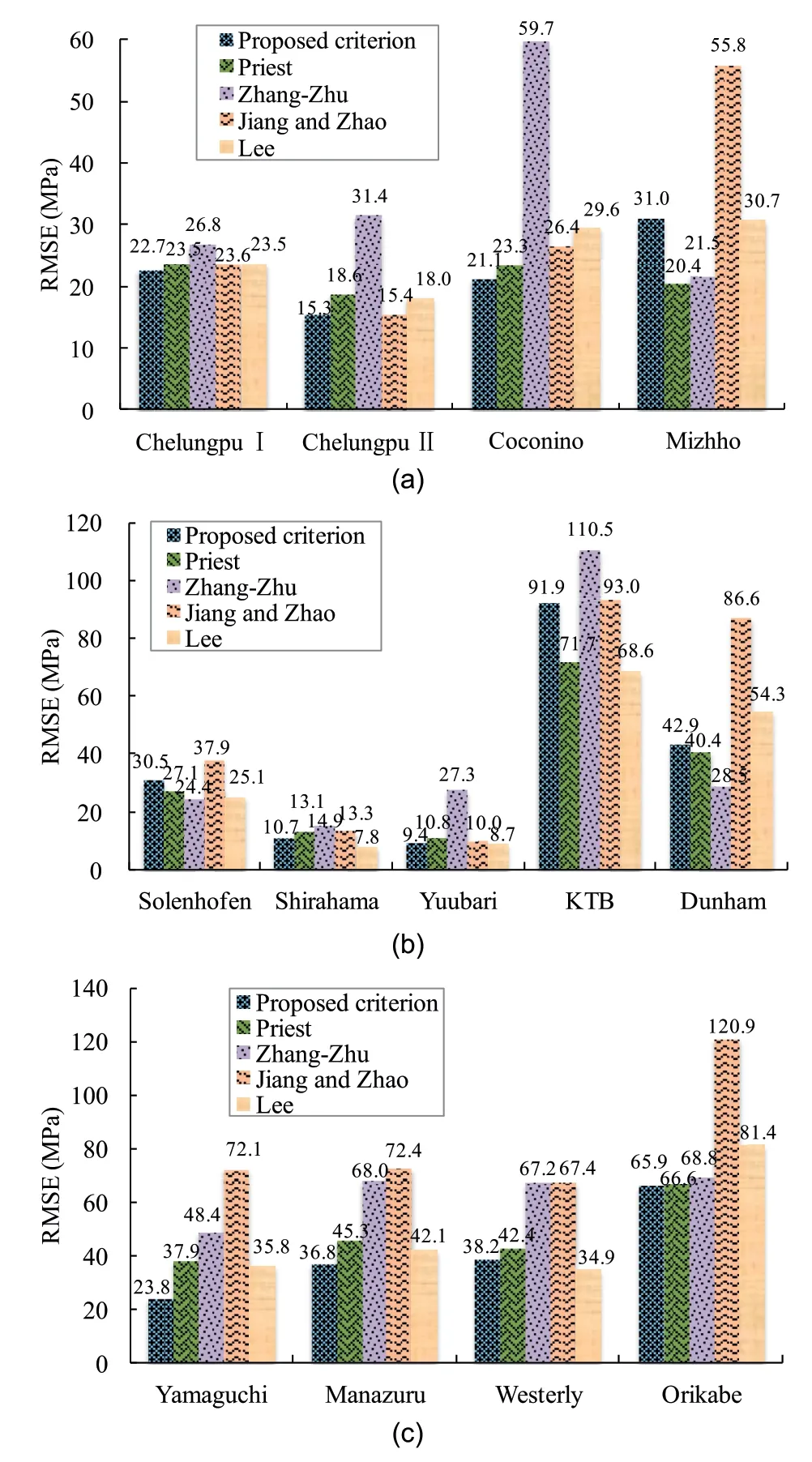
Fig.10.Prediction errors of the five criteria for 13 rock types:(a)Chelungpu siltstones I and II,Coconino sandstone and Mizhho trachyte;(b)Solenhofen limestone,Shirahama sandstone,Yuubari shale,KTB amphibolite and Dunham dolomite;(c) Yamaguchi marble,Manazuru andesite,Westerly granite and Orikabe monzonite.

To further clarify the merits of all criteria,Fig.11 summarizes the fitting curves of three rock types for all criteria.The proposed criterion can adjust b to provide best-fits for the rocks as illustrated in Figs.4-7 and 10.For some rock types,it may underestimate the strength in the high σ2range.In general,the experimental data of most of rocks can be bracketed by the prediction of the proposed criterion with b=0 and 1.Thus,with the proposed criterion as a reference,other criteria are quantified according to the envelopes in π plane.Fig.11 shows that the Pan-Hudson criterion underestimates the strength at low σ2and overestimates at high σ2,which gives the worst prediction.Its failure envelope in π plane crosses that of the proposed criterion,as shown in Figs.9 and 12.The Zhang-Zhu criterion can be approximated by the proposed criterion with about b=0.45 at the low Lode angle,and crosses the loci of the proposed criterion at high Lode angle,as shown in Fig.12.Hence,it would overestimate the strength at high σ2,as illustrated in Fig.11.In the range of low σ2,it works well for the strong σ2dependence of rocks (Fig.11c)and overestimates for the slight or moderate σ2dependence(Fig.11a and b).For the Lee criterion,its envelope lies between the envelopes of the proposed criterion with b=0 and 1,and is close to that of the Zhang-Zhu criterion at low Lode angle.The Lee criterion can predict the rocks with moderate σ2dependence well.For the Jiang-Zhao criterion,it can be approximated by the proposed criterion with about b=0.5 at Lode angle approaching 30°and b=0.3 in other cases,as shown in Fig.12.For the strong σ2dependence of rocks,the Jiang-Zhao criterion underestimates the strength(Fig.11b and c)and works well for the slight or moderate σ2dependence (Fig.11a).The Priest criterion fits the measured data for almost the three rocks better than other criteria except the proposed criterion.However,it yields a monotonically increasing strength(Fig.11),which cannot reproduce the effect of σ2on rock strength in the high σ2range.This fact maybe lead to the greater misfit provided that the true triaxial test data are sufficient from σ2=σ3to σ2=σ1.

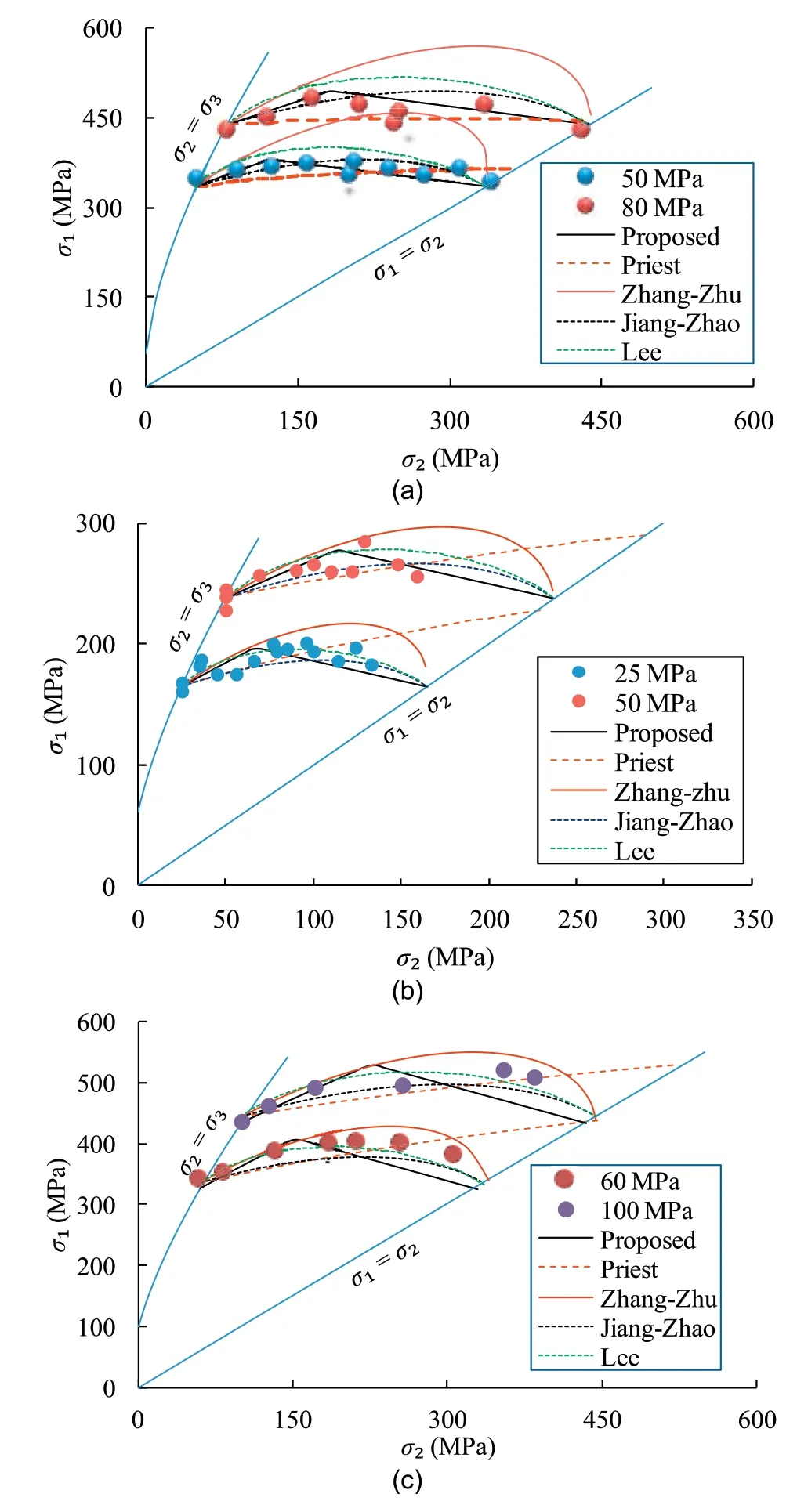
Fig.11.Comparison of fitting solution of the different criteria for (a) Coconino sandstone,(b) Yuubari shale,and (c) Mizhho trachyte.

Fig.12.Comparison and relationship of the different strength criteria in π plane.

Fig.13.Failure envelopes of simplified Priest criterion with different ω values in π plane.

Note that the proposed criterion and the simplified Priest criterion need an additional parameter.Comparatively,the proposed criterion can reproduce the results of true triaxial tests on rocks.The proposed criterion also has the obvious limitations,such as the non-smooth failure envelope,and the same predicted strength at σ1=σ2and σ2=σ3.In addition,Priest (2005) suggested that the value of ω in Eq.(6) ranges from 0 to 1.However,we find that the loci of the Priest criterion are non-convex in π plane when ω>0.5,as shown in Fig.13,as that of the Zhang-Zhu criterion,which conflicts the Drucker convex postulation (Drucker,1956).Furthermore,it would overestimate the strength of rock in triaxial tension state(σ1=σ2)when ω>0.5.Therefore,we suggest that the rational range of ω in Eq.(6)should be 0-0.5 rather than 0-1.Note that it would produce a strength reduction with the increase of σ2when ω is small (Priest,2010),which can also be illustrated by the failure envelopes in π plane as indicated in Fig.13.

5.Discussion and generalization

Fig.14.Relationship between b and σc for the proposed 3D HB criterion.

As illustrated above,the proposed criterion seems to be more versatile than some existing 3D HB criteria.However,it also has some limitations,such as an additional required parameter b.As we all know,one of the philosophies in developing a generalized strength criterion lies in predicting rock strength from readily obtainable strength parameters,for instance,from uniaxial or conventional triaxial compression tests.The proposed criterion requires an additional b value using the true triaxial test data,which would limit its application.The true triaxial tests are difficult to be performed and it would be preferable to conduct the uniaxial test and conventional triaxial tests.Herein,we will investigate the possibility of combining the uniaxial and triaxial test data to determine the value of b.After examining σ2dependence on strength of the published 13 rock types,one can see that the rock types with higher UCS have stronger σ2dependence on strength.Furthermore,the greater b in the proposed criterion is needed to describe the stronger effect of σ2on strength.These evidences suggest that the parameters b and σcshould remain a substantial relationship.

Fig.14 shows the curve of b plotted against σc.It indicates that b is influenced by the value of σc.The greater b is corresponding to the higher σc.An exponential function can be fitted through the data points as shown in Fig.14.The function is expressed as

Thus,the value of b can be calculated from Eq.(10)by using the UCS rather than the true triaxial test of rocks.Eq.(10)is plotted as a solid line in Fig.14.It indicates that all the data,except for that ofthe Yamaguchi marble and Westerly granite,converge around the solid line of Eq.(10).

The comparison of predictions using best-fitting b and Eq.(10)is conducted to explore whether it is reasonable or not to obtain the parameter b from Eq.(10).The RMSE is still used as a misfit index to evaluate the feasibility of Eq.(10).The misfits are summarized in Table 3.The misfits from Eq.(10) are 14.23%,75.98% and 93.37%greater than that from the true triaxial test for the KTB amphibolite,Yamaguchi marble and Westerly granite,respectively.For other rocks,the misfits are only 0%-5.87% greater than the best-fitting solutions,as shown in Table 3.In order to clarify the feasibility of Eq.(10) further,the misfit is compared with that of other criteria shown in Fig.10.It can be found that the proposed criterion with Eq.(10)still can achieve a good fit to most of rocks,especially to the Chelungpu siltstones II,Coconino sandstone,Manazuru andesite and Orikabe monzonite.The comparison suggests that Eq.(10) is reasonable and can be adopted to determine the value of b.In addition,the fact that the proposed criterion does not require a recursive numerical strategy to calculate the rock strength makes it extend the application of the original HB criterion more easily than other 3D HB criteria.In some cases,the criterion can discuss the range of solution to problems by changing b values instead of giving a fixed result.Note that the proposed criterion has some limitations as clarified in Section 2.

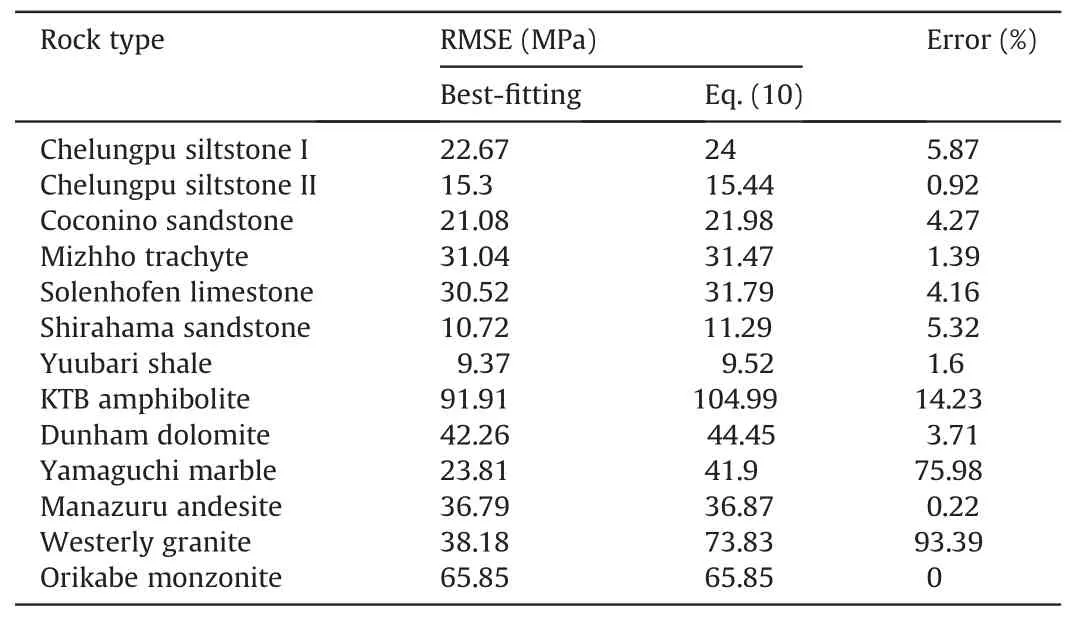
Table 3Comparisons of the predictions using best-fitting and Eq.(10) for all rocks.

Overall,all the parameters in the proposed criterion can be determined as the HB criterion does.It is important to appreciate that the proposed criterion does not need parameter adjustment or adopt curve fitting strategies to determine b in the absence of true triaxial test data,which is very helpful to generalize and utilize the proposed criterion.

6.Conclusions

By investigating the published true triaxial test data of various rock types,the effect of σ2on rock strength is identified.For most of the collected rock types,the strength increases with the rise of σ2until it reaches a peak level beyond which it follows a drop in strength as σ2approaches the magnitude of σ1.The role of σ2is approximated through a linear interpolation with σ1and σ3,respectively in different ranges of σ2based on the mechanism of σ2effect on rock strength.A new 3D HB strength criterion is proposed.It inherits the merits of the HB strength criterion and has a simple mathematical expression which can give an analytical solution of rock strength.It can represent a series of strength criteria when b takes different values.However,the proposed criterion predicts the same strength at σ2=σ3and σ1=σ2irrespective of b.The envelope of the proposed criterion is non-smooth which causes inconvenience in numerical simulation.

The proposed criterion is verified by the true triaxial tests on 13 published rock types.The results indicate that the proposed criterion works well on these rocks and can predict the results of the true triaxial tests.For comparison,several existing 3D HB criteria are selected to predict the data of all rocks.The failure envelopes of these criteria in π plane are also compared.In spite of the fact that the σ2dependence on strength varies for different rock types,the proposed criterion still provides the best-fit for most of rock types.It demonstrates that the proposed criterion works better and seems to be more versatile than the other criteria.

For the generalization of the proposed criterion,a substantial relationship between b and σcis found,which means that all the parameters of the proposed criterion can be determined as the HB criterion does.The proposed criterion can still work well if only the data from the uniaxial and triaxial tests of rocks are available.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This work was supported by the Key Research and Development Program of Shaanxi,China(Grant Nos.2019SF-231and 2020SF-394)and the Natural Science Foundation of China(Grant No.41630639).