基于核偏最小二乘法的湿法冶金萃取过程建模

陈 溥

(柳州铁道职业技术学院，广西 柳州 545616)

目前，国内外有关铜溶剂萃取过程中的建模研究较少，建立使用模型对于萃取过程中的自动控制有重要意义[1-5]。建立关键生产指标预测模型，对萃取过程的控制和优化至关重要，但影响过程操作的重要动力学传质速率无法测量。研究提出了一种适用于铜萃取过程中的结合机理模型和数据模型的混合模型。该模型由参数未知(传质速率)的机理模型和参数未知的数据预测模型组合而成。利用核偏最小二乘法(kernel partial least square，KPLS)建立传质速率预测模型，通过仿真与BP(back propagation)神经网络的混合模型进行对比分析。

1 铜溶剂萃取过程概述

铜萃取过程可分解为萃取、洗涤、反萃取3个阶段[6-7]。

萃取阶段：含有铜离子的水相与有机相混合，铜离子被萃入到有机相[8]。洗涤阶段：负载有机相用洗涤剂洗涤，将夹带的金属离子洗出有机相。反萃取阶段：用反萃取剂对洗涤后有机相进行反萃取，使铜离子返回水相。

影响铜溶剂萃取过程的因素有相比、温度、水相pH、萃取剂浓度、被萃取金属离子浓度等[9-10]。

2 混合建模

铜萃取过程机理模型的未知参数实际上无法测量，所以，提出了一种混合模型。该模型将机理模型和数据模型相结合，由参数(传质速率)未知的机理模型和参数未知的数据预测模型组成[11]。用KPLS法分别建立数据预测模型。

2.1 动态机理模型

动态机理模型描述萃取过程中组分浓度随时间的变化，是溶剂萃取过程控制系统的依据，有助于实现组分浓度优化控制。

在建立动态模型之前，对于多级逆流萃取过程做出以下假设：

1)两相完全混合，并且仅在混合器中进行传质；

2)两相不混溶，澄清器没有返混和逆流现象；

3)传质系数、萃取平衡等温线参数和效率参数不恒定，根据离线测量估算[12]；

4)萃取过程中两相体积不变；

5)萃取过程中各组分浓度随时间变化，是时间的函数。

根据物料平衡关系，建立第i阶段萃取过程的动力学模型，见式(1)～(3)[13]。

(1)

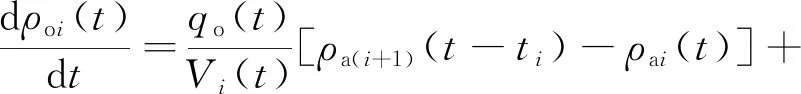
(2)

ρoi(t)=f(ρa(i+1)(t-ti),ρa(i+1)(t),qa(t),qo(t),A,B)。

(3)

式中：Vi—i级混合澄清器中混合相体积，L；qa、qo—水相、有机相流量，m3/h；ρa(i+1)为i+1级澄清器出口水相中Cu2+质量浓度，g/L；ρo(i-1)为i-1级澄清器出口的有机相Cu2+质量浓度，g/L；t、ti—萃取、滞后时间，h；Ki为第i级传质系数，L/s；ρoi(t)-ρo*i(t)为传质的驱动力，kN/m3；ρo*i为第i级达到平衡时有机相中Cu2+质量浓度(理想状态)，g/L，与上层Cu2+进入水相的浓度、下一阶段进入有机相的浓度、水相和有机相的流量、效率参数(α)和平衡萃取线常数A、B之间存在未知的函数关系，当i=N时，Ki[ρoi(t)-ρo*i(t)]为传质速率，g/(L·h)。

用McCabe-Thiele图计算平衡关系确定萃取级数，萃取部分理论平衡值根据水相和有机相中Cu2+及水相和有机相流量比确定。萃取平衡值x*计算公式[14]为

(4)

式中：a=-qa/qo；b=ρo(i-1)-aρa(i+1)，g/L。

α受有机相中试剂浓度和水相料液酸度影响。根据理论浓度平衡值x*(水相)和y*(有机相)、输入的水相浓度和有机相中Cu2+质量浓度ρin及实际Cu2+质量浓度平衡值ρout估算每个萃取单元的萃取效率。见式(5)，该值接近于1[15]。

(5)

当萃取达到平衡时，萃取过程处于稳定状态，见式(6)[16]：

q(tend)[ρin(tend)-ρout(tend)]-
KiV[ρout(tend)-ρ*out(tend)]=0，

(6)

一般来说，ρout(tend)-ρ*out(tend)非常小。用ε表示，ρout(t)-ρ*out(t)，导出传质系数K，见式(7)[17]：

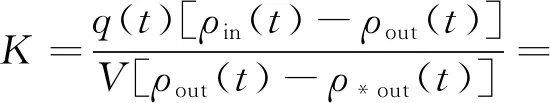
(7)

传质系数受多种因素影响，如操作条件、反应器尺寸等。在交叉参考微反应器中，铜的传质系数为31.12～214.34 L/s[18]；混合澄清器的K=50～400 L/s。

2.2 BP神经网络模型

BP神经网络有3层，输入层、输出层和隐藏层，每层有多个节点[19]。节点是神经元，神经元之间的连接线为权重。基本BP网络如图1所示。

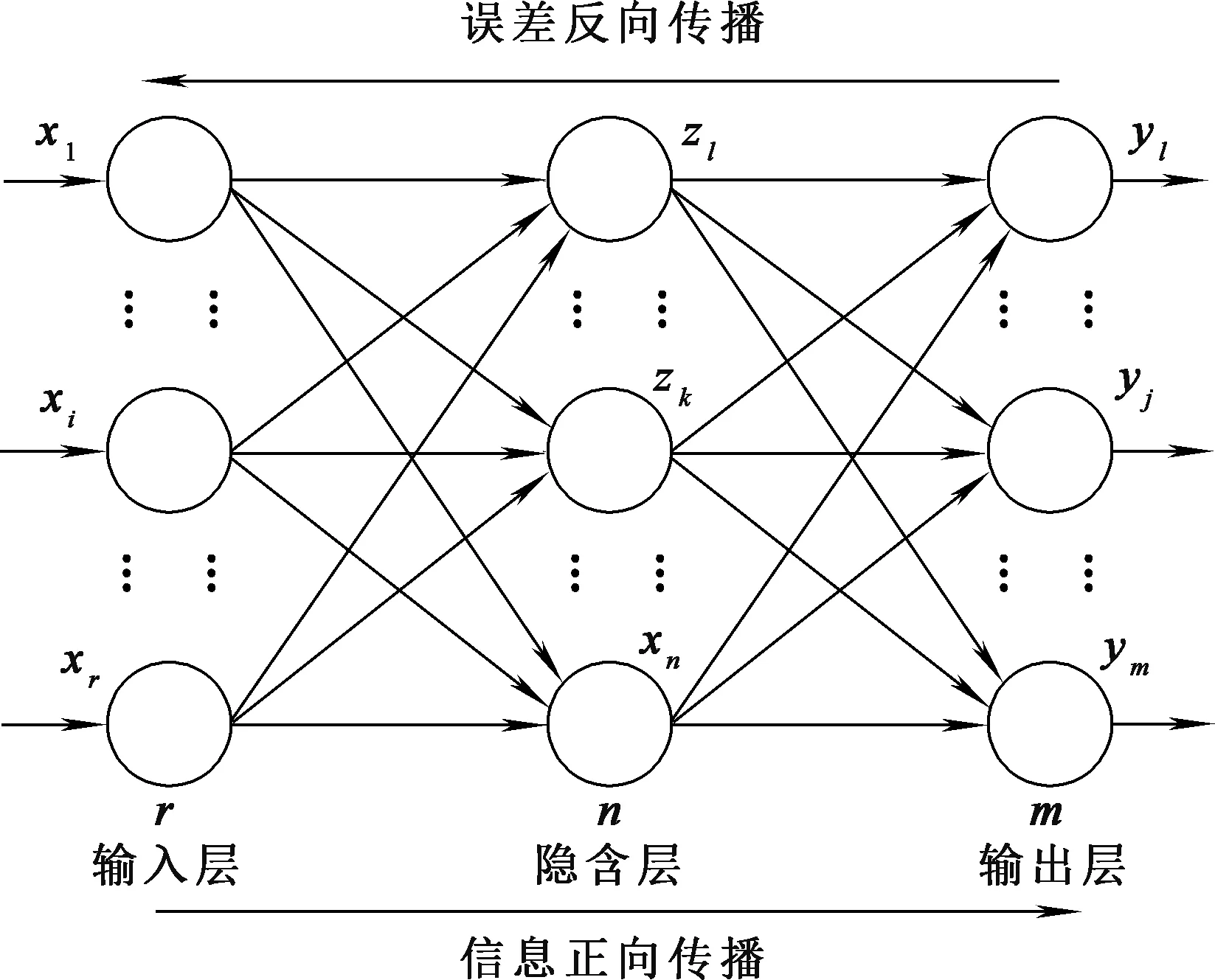
图1 基本BP神经网络模型

假设输入层、输出层、隐含层节点数分别为r、m、n；xi为输入层i神经元的输入值；zk、sk分别为隐含层第k个节点的输出值和净输入值；yj、sj分别为输出层j节点的实际输出和净输入值；vik、wkj分别为输入层i节点与隐含层k节点和隐含层k节点与输出层j节点之间的连接权值。

正向传输过程中，输出层和隐含层的输出计算公式见(8)～(11)[20]。

zk=f(sk),k=1,2,……,n；

(8)

(9)

yj=f(sj)，j=1,2,……,m；

(10)

(11)

在式(8)～(11)中，选择激励函数f(x)=1/(1+e-x)，其导数为f’=f(1-f)。通常，误差函数(也称性能函数)E可以评估网络性能，E越小，网络性能越好。见式(12)，性能函数取均方误差函数。

(12)

误差反向传播将误差定义扩展到隐含层至输入层，见式(13)。

(13)

标准BP算法用梯度下降法来调整层间权重，见式(14)、(15)。

(14)

(15)

如果η较大，则修正速度快且易振荡；η较小时，则会导致网络训练时间长且收敛速度慢。η取值范围为0.01～0.8。BP算法流程如图2所示。

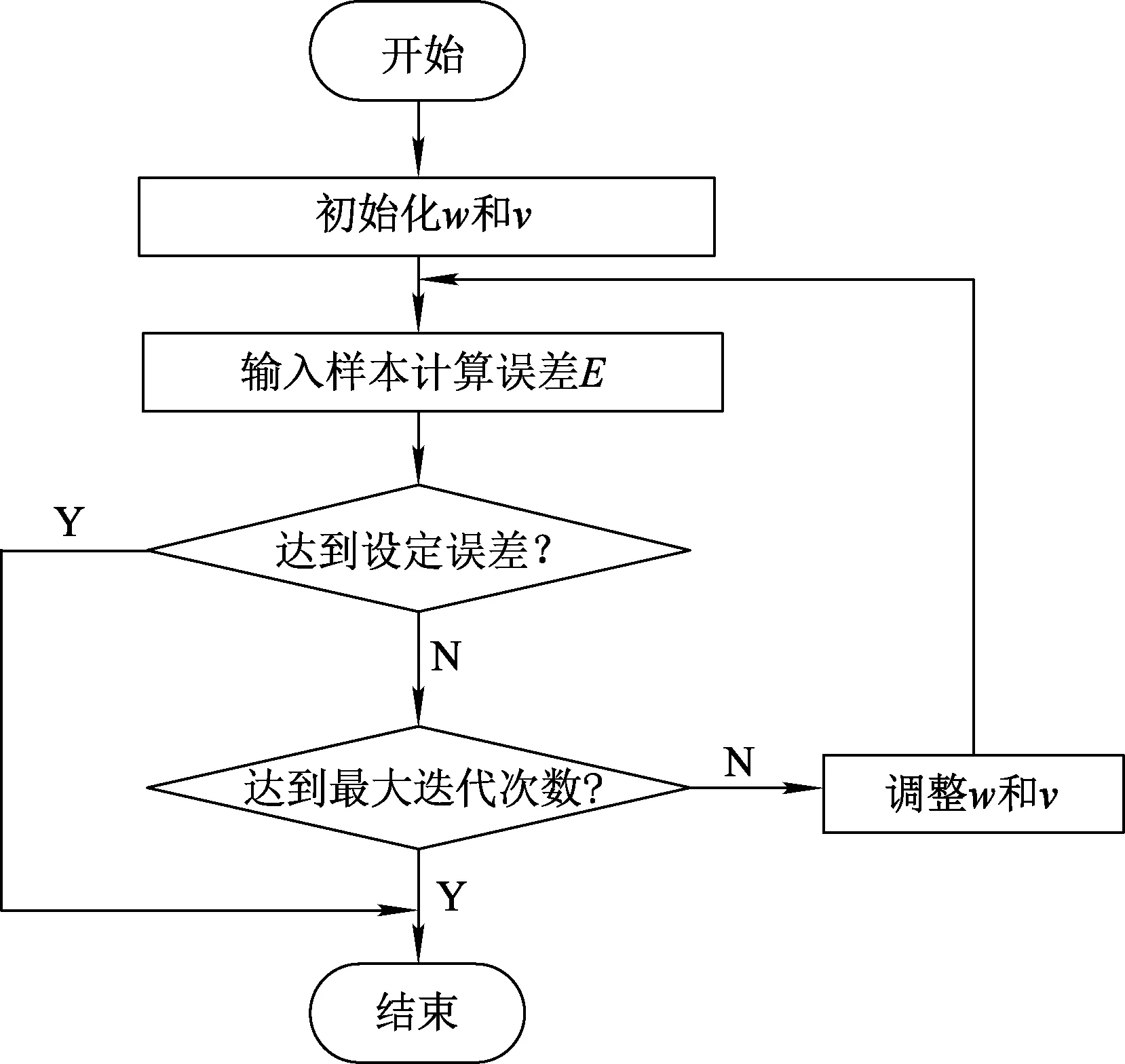
图2 BP算法流程

2.3 核偏最小二乘法

偏最小二乘法(partial least square，PLS)是一种多元统计数据分析方法，可以解决普通多元回归方法无法解决的许多问题[21]。偏最小二乘方法假定感兴趣区域由一些潜在向量决定，这些向量是观测值的线性组合。假设有向量个因变量{y1,y2,…,yq}和p个自变量{x1,x2,…,xp}，观测n个样本点。X={x1,x2,…,xp}为输入变量的n×p矩阵；Y={y1,y2,…,yq}为相应输出变量的(n×p)矩阵。

首先，从X和Y中提取得分向量t1和u1(t1为x1,x2,…,xp的线性组合，u1为y1,y2,…,yq的线性组合)，要求t1和u1尽可能代表矩阵X和Y。

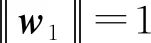
t1=Xw1；

(16)

u1=Yc1。

(17)

然后，建立X对t1、Y对u1的回归方程，见式(18)(19)，且满足式(20)。

X=t1p1T+E1；

(18)

Y=u1q1T+F1；

(19)

u1=f1(t1)+r1，

(20)

式中，p1、q1分别为得分向量对应的载荷向量。

残差计算公式为(21)(22)。

E1=X-t1p1T；

(21)

F1=Y-u1q1T。

(22)

提取E1和F1得分向量，重复上述算法，直到得到第a个得分向量。残差Ea和Fa几乎没有任何关键信息。

由于铜萃取过程的动力学反应为非线性，PLS算法无法解决该问题，因此引进核偏最小二乘法。该方法是在核希尔伯特空间(Reproducing Kemel Hilbert Space，RKHS)中建立的机器学习算法之一。用该方法建立模型的目的是最小化结构风险，即在(RKHS)中寻找最优模型。KPLS遵循PLS基本思想，它们的区别在于PLS建立从属变量(y)和自变量(x)之间的相关性，而KPLS仅将自变量(x)投影到RKHS上，并且在RKHS中找到Ф(x)和y的相关性。KPLS的本质是在特征空间中构建PLS模型，有效地获得非线性回归模型。

同样，观测n个样本，所谓“核技术”，实际上是Ф(xi)TФ(xj)=K(xi,xj)。可以看到，ФФT为所有映射的输入数据点{Ф(xi)}n(i=1)之间交叉内积运算的核Gram矩阵K(n×n)，因此，可以用核函数来代替非线性映射。通常，当提取t分量后，矩阵见式(23)。

K←(I-ttT)K(I-ttT)=
K-ttTK-KttT+ttTKttT，

(23)

式中，I为n维单位矩阵。对PLS算法的非线性校正也可以得到类似的KPLS算法。修正的结果是从KYYT和YYT矩阵中提取得分向量t、u，步骤如下：

步骤1，随机设定初始值u(可设定为u等于Y列中的任意一列)；

步骤2，根据t=ФФTu=Ku，计算得分向量；

步骤3，根据c=YTt计算系数向量；

步骤4，计算得分向量；

步骤5，重复2～5步，直到收敛；

步骤6，矩阵K和Y进行缩并，K←(I-ttT)K(I-ttT)，Y←Y-ttTY；

步骤7，返回步骤1，计算下一个t、u。

回归系数矩阵B通过公式(24)计算得到，

B=ФTU(TTKU)-1TTY。

(24)

预测的训练数据见式(25)，

Y*=ФB=TTTY。

(25)

KPLS算法流程如图3所示。

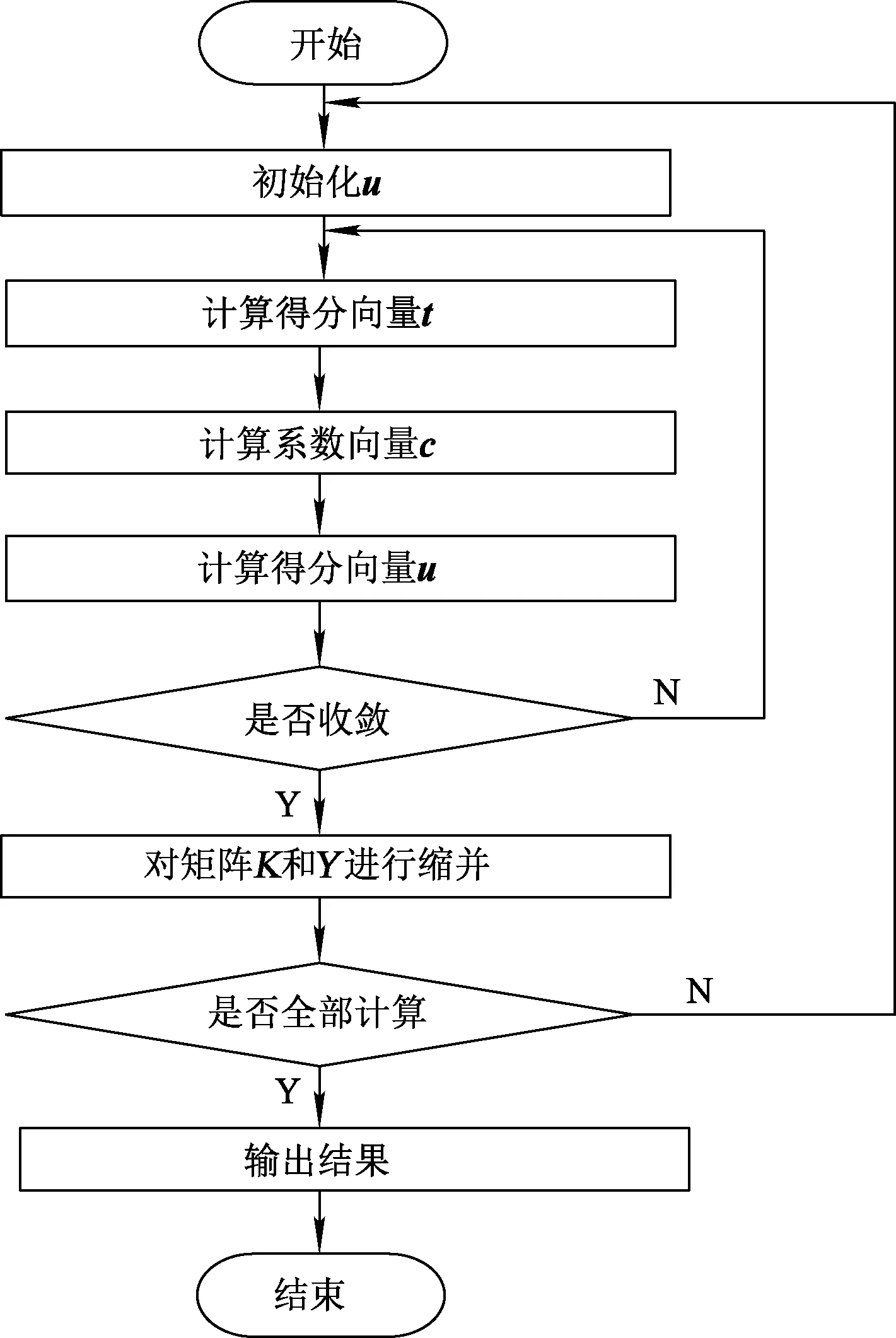
图3 KPLS算法流程

3 仿真结果与分析

3.1 仿真参数

混合模型由参数未知(传质速率)的机理模型和参数未知的数据预测模型组成。通过BP神经网络和KPLS建立传质速率预测模型，并与机理模型形成混合模型。数据模型是黑盒模型。在未知传质速率模型结构和相关参数情况下，可以获得传质速率背后的过程变量之间的复杂关系，从而降低建模难度。在考虑过程的物理特性的同时，机理模型和数据模型组合有效地利用了相关的数据信息。这种混合模式具有很高的精度，适合于实际工业生产过程，为铜溶剂萃取工艺先进控制系统的开发和在线优化奠定了基础。铜萃取混合模型如图4所示。

图4 铜萃取过程混合模型

计算机为CPU i5-2450m，内存为8 Gb。仿真软件为matlab2018。实验室实际采集200组萃取过程稳态数据，100组用于训练，100组用于测试。为了验证和比较上述预测模型性能，利用以下3个性能指标对各算法性能进行评价。

1)均方根误差(RMSE)

(26)

2)平均绝对误差(MAE)

(27)

3)平均绝对百分比误差(MAPE)

(28)

式中：xi和x*i分别为铜传质速率实际值和预测值，M为预测样品总数。

3.2 仿真分析

建立传质速率黑箱模型，输出传质速率预测值。黑箱模型的输入对应于传输速率估计值的影响因素。相同条件下，利用BP神经网络和KPLS对传输速率进行建模。图5为BP神经网络及KPLS黑箱模型预测效果。可以看出：BP神经网络的训练效果良好，表明BP神经网络黑箱模型具有准确的预测能力，非线性映射能力较好；但训练中收敛速度较慢，并且在训练集比较小时，容易发生过拟合；KPLS将初始输入映射到高维特征空间，有效解决了非线性回归问题。

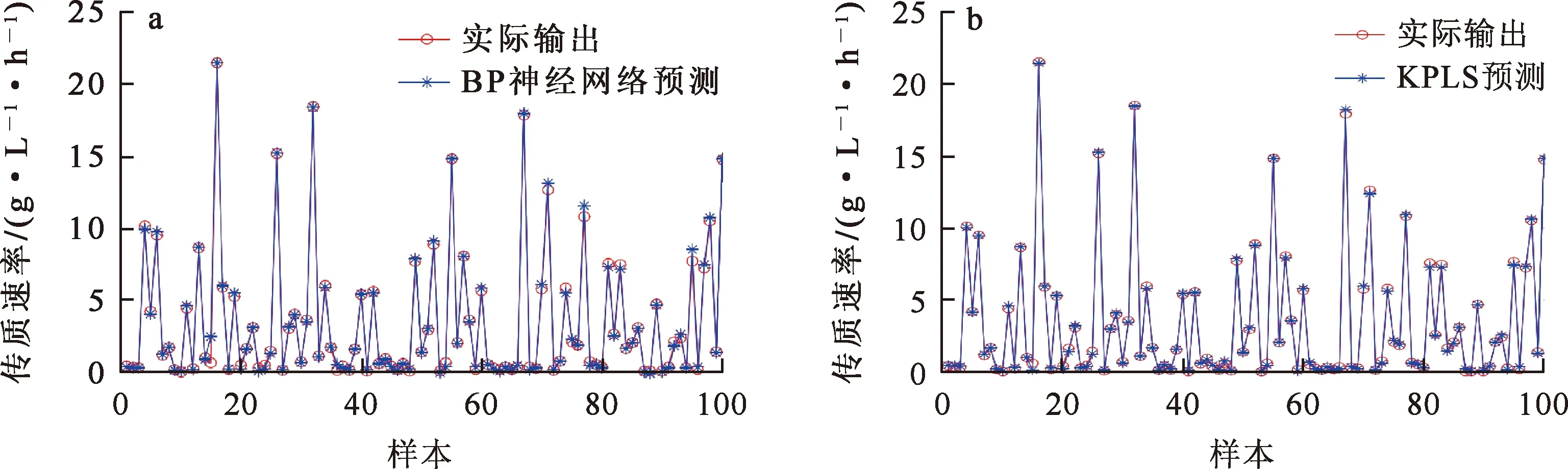
a—BP神经网络预测模型；b—KPLS预测模型。图5 黑箱预测结果

2个数据模型性能指标见表1。

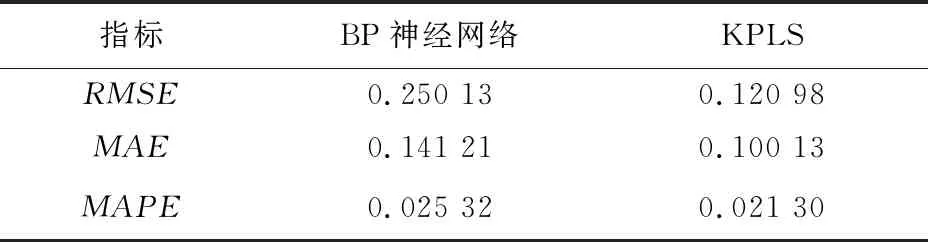
表1 BP神经网络和KPLS数据模型预测性能指标

数据模型的正确性在混合模型构建中起重要作用。以上2种算法能够准确预测传质速率。由表1性能指标对比结果看出，KPLS方法效果较好。数据模型的准确性解决了传质速率无法测量的问题，这为建立更接近实际过程的混合模型奠定了基础。

对比单一模型和混合模型预测结果可以说明上述铜萃取过程混合模型的有效性，对比结果如图6所示，各模型的性能指标见表2。

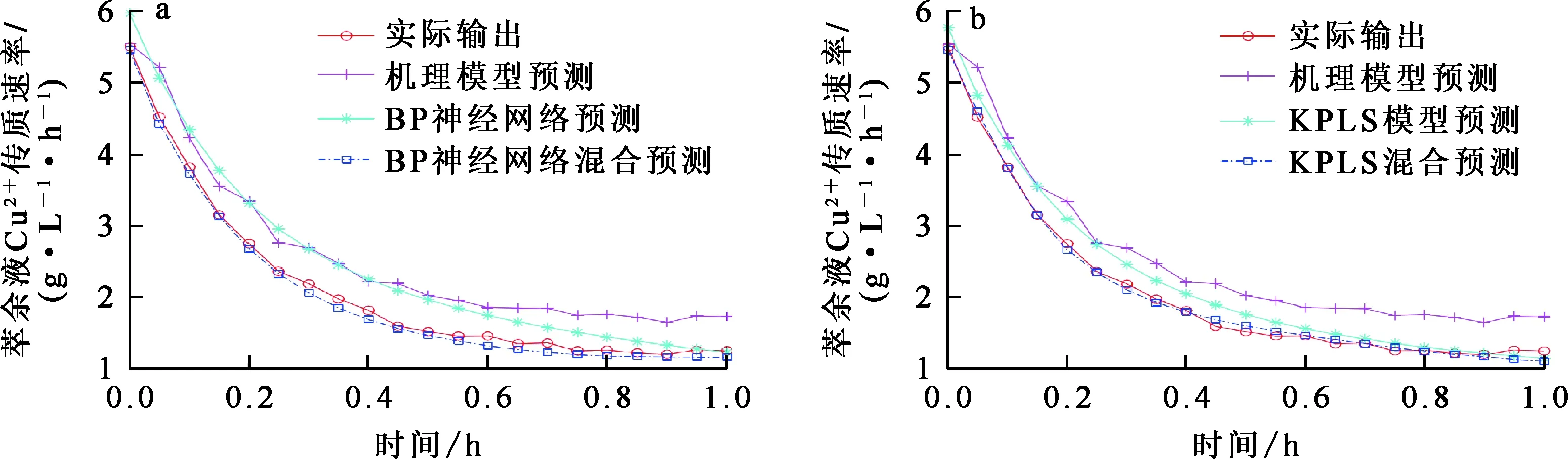
a—BP神经网络；b—KPLS。

表2 单一模型和混合模型预测性能指标

由图6看出：机理模型能够很好预测过程趋势；然而，由于萃取过程较为复杂，预测结果与实际值误差较大；单一数据模型相对于机理模型需要考虑的因素更多，预测效果优于机理模型。由于数据模型不使用已知的经验知识，仅依赖数据获得输入输出之间的关系，纯数据模型的泛化能力差，所以预测值和实际值误差较大。混合模型将数据模型和机理模型优点相结合，精度较高，泛化能力强，有良好的预测效果，对铜溶液萃取工艺先进控制系统的开发和操作优化有一定参考性。基于KPLS的混合模型性能较优，RMSE为0.066 52，MAE为0.043 12，MAPE为0.019 82；对铜溶液萃取工艺先进控制系统的开发和操作优化有一定参考性。

4 结论

提出了一种混合模型，该模型由存在未知参数(传质速率)的机理模型和未知参数的数据预测模型组成，通过数据模型预测机理模型的未知参数(传质速率度)。混合模型性能的分析结果表明，基于KPLS的混合模型性能较优，均方根误差、平均绝对误差、平均绝对百分比误差都较低，可作为铜萃取过程中自动控制系统开发的依据。考虑到实验室设备和数据规模，建模方法还处于初级阶段，还有待进一步完善。