整体感知 深度建构——特级教师蔡宏圣《数的相等》教学片断赏析

文|张晓锋

特级教师蔡宏圣在今年三月执教了一节非常精彩的《分数的基本性质》。蔡老师打通知识之间的关联，将整数的相等、小数的相等与分数的相等有机联结，直指数的相等的核心本质，将课题定为《数的相等》。文章通过片断来洞悉蔡老师设计与教学之匠心独运。

片断一：关联旧知，感悟整数、小数相等之理。

师：同学们，屏幕上有四幅图，谁和谁相等？3和3为什么相等？3为什么不和30相等呢？都是三粒珠子呀！（呈现课件）

生：一个3在个位，一个3在十位，计数单位不同。

师：是什么不同呢？3和4单位一样，为什么还是不相等呢？

生：4比3多1个单位。

师：总结一下，因为计数单位的个数不同，所以3和4不同。因为3和3单位相同，个数相等，所以3只能和自己相等。

师：同学们已经知道0.3和0.30相等。0.3的计数单位是0.1，它有多少个计数单位？（呈现课件）

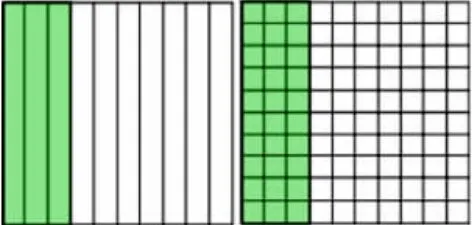
生：0.3有3个0.1。

师：0.30的计数单位是多少？它有多少个计数单位呢？

生：0.30的计数单位是0.01，它有30个这样的计数单位。

师：计数单位不同，它们怎么还相等呢？

生：数量把大小弥补了。

师：（呈现课件）它才3个，它是30个，怎么还相等呢？

生：个数少的计数单位大，个数多的计数单位小，能相互抵消。

师：相互抵消，这个词用得好！这是我们学过的小数的性质。

（补充板书：0.1→0.01“÷10”，3个→30个“×10”）

师：我们把整数的相同理清了，把小数的相同也理清了。下面我们要探索分数的相同。如果单位变了，个数变了，还会相等吗？

【赏析：新的教学理念倡导教师用“联系的观点”指导数学教学，并以此促进学生的深度学习、系统建构，培养学生的高阶思维。蔡老师洞悉数学相关知识的联结之理，他以整体视角，纵横关联，结构化设计，让学生能够感受整数里的相等和小数里的相等都要分析计数单位与计数单位的个数之间的关系，堪称“培根”之作。这样的设计能让学生清晰地感受到知识之间的内在关联，是一种结构化教学。一个“相互抵消”，将这节课的重点——“个数相同，方向相反”凸显了出来。】

片断二：聚焦研究，探究分数相等之理。

师：分母从2变到4，乘了2，单位之间是什么关系？

生：分母变大，就是分的份数变多，每份变少了。

师：单位还能怎么变？

生：分母乘3，单位缩小3倍。

师：怎么知道是3倍关系的？

生：分子都是1，只要看分母，分母从2到6，乘3。

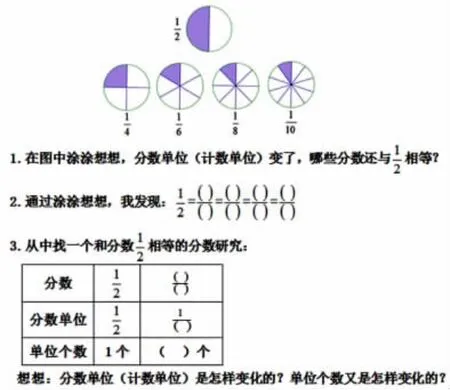
（呈现课件）

生：（齐说）有无数个。

师：为什么这样就能相等？分母乘6意味着什么？为什么分子也乘6？

师：第一种方法同时乘2；第二种方法，分母是分子的2倍，道理是什么呢？

生：分数和小数一样，计数单位的大小与个数是相反的。

师：分母除以6，就是单位扩大6倍，分子要缩小6倍，所以除以6，得到1。分母乘几就是把单位变小，个数变多，分子也得乘。分母除以几，就是把单位变大，个数变少，分子也得除。两个分数，计数单位间的倍数关系和个数间的倍数关系相同，而且成相反倍数关系时，两个分数大小不变。

补充呈现：

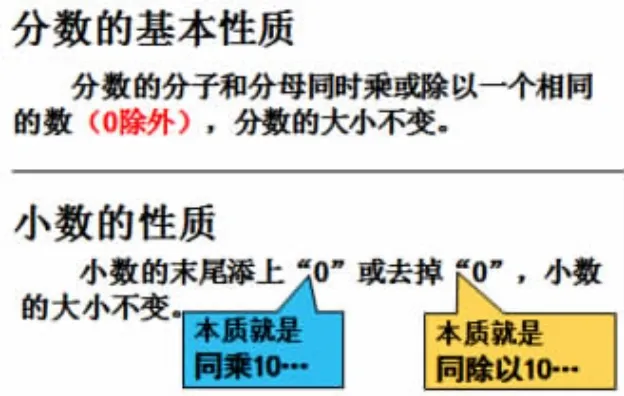
【赏析：华东师范大学教育学部杨向东先生认为，“合理整合儿童所处的现实生活和学科世界，以真实问题和现实情境为载体开展课堂教学，让他们在彼此关联的经验活动和学习共同体中进行意义建构，关注课堂学习过程中的实践、反思、质疑和互动，批判性思维、创造性、合作或交流等很多素养自然就融合在其中了。”蔡老师将分数基本性质的形成过程与分数的意义有机联结，促进学生深度建构。他从分数和开始，让学生积累“单位变大，个数变少；单位变小，个数变多”的体验。然后从等，鼓励学生独立思考、参与小组交流，深切地体会分母怎么变，分子也得怎么变，分数才相等。关键是让学生体会到分数单位变大了，分数单位的个数变少了，才能实现分数相等，把分数的相等和分数的基本性质、分数的意义进行有效的联结，让学生真正理解分数相等背后的道理。涂色活动意在引导学生聚焦观察这些分数的分数单位个数与分数单位大小之间的关系。最后，蔡老师引导学生将分数的基本性质和小数的基本性质进行对比沟通，用问题“它们一样吗？添0是干什么呀？”引导学生理解“把单位变小，把个数变多”，让学生在多次感悟中打开知识间的通道。知识是整体的，学生的思维也是整体的、有结构的。学生的理解最终都直指核心本质——从表面看，分数的分母和分子的倍比关系一致，分数相等；从本质看，分数单位变大，分数单位的个数变少；分数单位变小，分数单位的个数变多，相互抵消，分数相等。】

片断三：精要练习，加深学生对分数相等本质的感悟。

完成练习1：

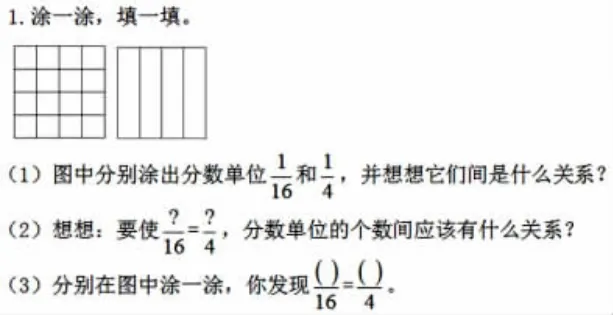
师：分母之间是4倍关系，分数单位之间就是4倍关系，分数单位的个数之间也是4倍关系，不过是反的。还有答案吗？

师：道理呢？分子、分母同时除以4，相当于把单位扩大了4倍，个数呢？对呀，个数缩小了4倍。

师：分数单位之间都是4倍关系，为什么会有三组呢？

……

【赏析：重庆市教育科学研究所李光树指出，理解是学习的关键和核心，只有深度理解了知识才能有技能的掌握、能力的发展，以及良好素养的形成。蔡老师的练习设计较为开放，为学生的理解而教。他精心设计的练习很好地指向本节课的核心——数的相等。通过一组有效的练习，让学生在理解分数相等之理的基础上，在更为本质的层面上领悟分数的基本性质，完整经历数学化的过程。】

片断四：反思回顾，引领学生整体建构认知。

（呈现课件）蔡老师从回顾“3和3为什么相等？”这个问题入手，呈现结构化的回顾课件，引导学生谈学习感悟。

师：这个环节的学习，你有什么体会？

师：我们回顾了整数相等、小数的性质，学习了分数的基本性质，这些都是数的相等，这些内容都与数的组成有关。通过学习，我们知道计数单位间的倍数关系和计数单位个数间的倍数关系相同，而且成相反倍数关系时，数就相等。同学们，越能把不同的知识联结起来，学习就越透彻！

【赏析：南京大学哲学系郑毓信教授强调：“数学对象的建构事实上是一种整体性的建构活动。或者说，数学的对象并非各个孤立的模式，而是整体性的‘建构’。”全课回顾的时候，蔡老师把整数的相等、小数的性质、分数的基本性质进行整体联结，让学生感受到这些内容都是关于数的相等的知识，有利于学生建构关于数相等的统一认识。蔡老师以“越能把不同的知识联结起来，学习就越透彻。”让学生感受结构化学习、关联性思考的价值。】