聚焦“四力”培育 提升核心素养

文 夏向阳

小学数学核心素养是指学生在接受数学教育的过程中，逐步形成的适应个人终身发展和社会发展需要的必备品格与关键能力。如何发展学生的核心素养，培养学生的实践能力和创新精神？笔者经过多年的思考和实践，通过培育学生主动的探索力、积极的提问力和辩证的批判力、理性的反思力等教学策略，得到了良好的教学效果。

一、培育主动的探索力，激发旺盛的内驱动力

《数学课程标准》（2011版）提出学生学习是一个生动活泼的、主动的和富有个性的过程，自主探索是学习数学的重要方式，学生应当有足够的时间和空间经历观察、实验、猜测、推理、验证等活动过程。探索力是基于儿童具有好奇心、求知欲等心理天性，独立或与他人合作参与特定的数学活动，通过大胆尝试，发现对象的特征及其与相关对象的区别和联系，主动寻求有效的问题解决方法，获得一定的理性认识，培养学生不畏困难，坚持不懈的探索意识和探索精神，形成初步的探索能力。

笔者教学人教版数学五年级上册一个数（0除外）乘大于1的数，所得的积大于这个数的教学片断，让学生采用猜测、验证等探索性过程，从而习得一种探索力。

师：2×（）＞2。

生1：2×（5）＞2。

师：能不能填比5再小一点的数？

生2：2×（2）＞2。

生3：2×（1.5）＞2。2×1.5=3，3＞2。

师：能不能填比1.5再小的数？

生4：2×（1.2）＞2，2×1.2=2.4，2.4＞2。

生5：2×（1.1）＞2，2×1.1=2.2，2.2＞2。

师：能不能填比1.1还要小的数？

生6：2×（1.01）＞2，2×1.01=2.02，2.02＞2。

生7：2×（1.001）＞2，2×1.001=2.002，2.002＞2。

生8：2×（1.000001）＞2，2×1.000001=2.000002，2.000002＞2。

师：你们觉得还能填更小一点的数吗？

生9：2×（大于1的数）＞2。

师：你们同意吗？

生：同意。

师：那你们能用一句话进行总结吗？

生1：一个数乘大于1的数，所得的积比这个数要大。

生2：一个数不包括0。

师：说说你的想法。

生2：0乘以大于1的数，所得的积和这个数0相等，所以这个数不能是0。

师：你想得很周到，一个数的前提条件是不可以为0，这样所得的积比这个数要大。

师：你们是否思考过为什么一个数（0除外）乘大于1的数，所得的积比这个数要大？

生1：一个数（0除外）乘1所得的积等于这个数，而这个数乘大于1的数，说明是求这个数的1倍多、2倍、2倍多……所得积比这个数一定要大。

师：下面把刚才的学习过程进行梳理，我们采用“猜测——验证——总结——说理”的方式得出了一个数学结论，这是学习数学的一种重要方式，希望同学们能够灵活运用、举一反三。

师：根据2×（）＜2填空，你也能得出一个数学结论吗？

以上教学片断中创设填空的形式，让学生通过填写合适的数慢慢逼近只要填“大于1的数”，所得的积都比这个数要大。笔者把这个数学结论的习得设计成一个探索的流程，让学生通过不经意间的猜测、验证、小结，悟到数学结论，在不断完善、修正中提炼数学结论，并对这样的结论尝试说理、解释，让学生能够真正理解通透，进而能够灵活应用。

二、培育积极的提问力，挖掘深度的联想思维

《数学课程标准》（2011版）明确提出把“发现、提出问题”和“分析、解决问题”同时作为数学课程教学目标，凸显学生的问题意识，提高发现和提出问题的能力。学习数学必须要有问题，没有问题很难学好数学，不仅要能解决别人的问题，更重要的是自己要学会提问题。学习数学概念时要弄清为什么需要它，它与前面所学的哪些知识有联系，它与实际生活又有什么联系。在学习数学技能、方法、思想时，更需要深入发问，在回答中不断思考、不断理解、不断深入。在实际情境学习中，也需要有提出问题的意识。问题是创新的基础，培养学生的提问力就是培养学生创新意识的好办法。如果我们的教学限制了学生的思考机会，不仅可能会妨碍学生发现问题和提出问题水平的提高，时间久了还可能“减弱”学生发现和提出问题的兴趣和意识。

从课堂观察和学生发展情况看，“联想”是促进学生发现和提出问题的有效策略。在所有年级中，学生都有联想以前的经验来发现和提出问题的意愿，“联想”有效拓展了学生提出问题的角度，“经验”有效提高了学生提出问题的深度和实际意义。联想的经验可以是以前的生活经验，也可以是以前学习活动中得到的经验。

在三年级“购买水果”的教学中，学生虽然找到了“联想”这种好办法，但学生运用联想的水平是不同的。有的学生也在运用联想，但他的联想是在一个问题上的复制，比如从苹果想到梨子、火龙果、香蕉、哈密瓜等，问题的本身没有改变，这种联想是简单的“复制”。而有的学生则是对问题情境所蕴含的相关因素的联想，是基于对事物本身的认识和理解基础上的一种联想，涉及水果价格、种类、质量、促销手段等，在发现和提出问题的教学中，要着力发展的是后一种联想，类似于实现“大跨度联想”。

三、培育辩证的批判力，彰显缜密的质疑品质

批判力是一种比较高级的思维能力，指在数学活动中能独立思考、独立判断，多角度、辩证地分析问题，做出理智的选择和决定，思维缜密、条理清晰，直面知识的本质和内涵，初步形成批判意识、批判精神和批判能力。长期以来，在我们的课堂教学中，教师、课本是绝对权威，学生通常只能无条件地服从和遵循。在这样的教育体制下，学生唯教师、唯课本的现象越来越严重，容易扼杀学生的批判精神和批判能力。随着新一轮课程改革的纵深推进，广大教师的教育教学理念和教学行为发生了根本性转变。学生是学习的主体，教师要呵护学生独立的见解，使学生愿意讨论，敢于质疑；学生和教师人人平等，互相尊重、互相学习、互相发展已成为教学共识。对新事物感兴趣，尝试去做一些对自己是新的、没有想过、没有做过的事情，用学过的数学方法解决问题成为教学常态。笔者曾经对六年级学生做过如下的一次问卷调查：

李师傅加工零件，下表是他4小时加工零件数的统计。

时间第1小时第2小时第3小时第4小时个数9111510292

根据上表中的信息，李师傅要加工1800个零件，20小时能完成吗？请说明理由。

问卷调查后笔者对学生的解答进行了整理：

方法1：（91+115+102+92）÷4=100（个），20×100=2000（个），2000个＞1800个，能完成。

方法2：（91+115+102+92）÷4=100（个），20×100=2000（个）。

如果李师傅20小时加工的工作效率和前4小时加工的工作效率相同，则能完成；如果工作效率不同，那就不能确定。

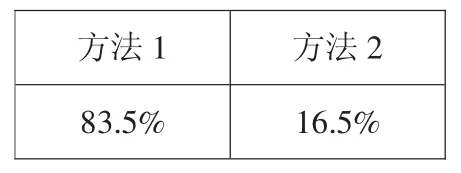
方法1方法2 83.5%16.5%

从以上表格中的数据我们可以得出，在学生的潜意识中，认为解决问题中提供的相关信息一般总是有用的，即使有时能正确区分出多余的已知信息，但部分已知信息还是为解答所用。这也充分说明，在学习材料、学习情境、学习任务等选择中，作为教师要有意识地挑选一些非常规的学习素材，让学生能够主动结合生活实际运用非常规思维来解答，培养学生的质疑能力，学会辩证、全面、科学、灵活地解决数学问题。

四、培育理性的反思力，生成稳固的高阶思维

反思力是指具有对自己的学习状态进行审视的意识和习惯，善于总结经验，能够根据不同的情境和自身实际，选择或调整学习策略和方法。乐学善学，勤于反思，学习意识的形成、学习方式方法的选择、学习进程的调控等都是反思力形成的表征和标志。

教学解决问题“用一根长为48cm的铁丝围一个长方形框架，已知长是宽的2倍。这个长方形框架的长和宽分别是多少厘米？”

很多同学会这样解答：

宽：48÷（2+1）=16（cm），长：16×2=32（cm）。

学生为什么会出现这样的错误解答？原因是学生只关注“周长是48cm”和“长是宽的2倍”这两条相关信息，而忽视了长方形由两条长和两条宽组成的特征。如果教师直接指出学生的错误及原因，揭示正确的思路和算式，大部分学生能理解。但仍然有一部分学生下次碰到类似的数学问题时还会再次发生错误。那么，如何正确处理这一典型错误呢？笔者采取了如下的教学方式：

师：读了题目后，你知道了哪些相关信息？

生：一根长48厘米的铁丝就是长方形框架的周长。

生：长是宽的2倍。

师：请同学们独立解答。

生：宽：48÷（2+1）=16（cm），长：16×2=32（cm）。

师：这位同学计算出宽是16cm，长是32cm。是否正确，你们有办法进行检验吗？

生：这比较简单，长方形的周长=（长+宽）×2，所以相应的算式就是（32+16）×2=96（cm）。96cm和题目中的已知信息48cm不同，说明这样解答是不正确的。

师：那问题究竟出在哪里呢？

生：长方形的周长包括两条长和两条宽。48÷（2+1）=16（cm），这里的16cm指的是2条宽的长度，而不是1条宽的长度。因此，16÷2=8（cm）才表示1条宽的长度。同样道理，32÷2=16（cm），16cm就表示1条长。

师：下面请同学们也进行检验。

生：（16+8）×2=48（cm），48cm和题目中的已知信息一致，说明是正确的。

以上的教学片断，当学生列式解答后，笔者不是急于让学生通过讨论确定是不正确的，而是把计算出来的得数通过检验的方式，和已知的信息进行比较。然后，让学生深入分析、讨论究竟错在哪里？让学生进行自我反省，找出错误的真正原因，从而建构正确的解题思路。“验证——反思——重构”也是一种重要的学习方式，可以培养学生“从头想到尾”、“从尾推到头”的良好解题习惯，生成常态的高阶思维。