含柔性腹节的仿蚕机器人转弯运动建模与实验
马林坡,潘雪荧,王永娟,范丽萍
(1.南京理工大学 机械工程学院, 南京 210094; 2.苏州长风航空电子有限公司, 江苏 苏州 215151;3.江苏省海门中等专业学校, 江苏 南通 226100)
仿生机器人是指模仿生物、从事生物特点工作的机器人。在生物界中,存在着许多依靠自身的身体变形波传导来获得有效运动能力的动物,由于其特殊的运动模式和多自由度的身体结构,它们具有很强的运动稳定性和环境适应性。目前,仿生蠕动技术的研究已经成为当前仿生机器人领域研究的热点之一[1]。
仿生蠕动机器人具有接触面积大、离散性高的特点,使得对坑洼等地形具有更强的适应性和稳定性[2]。连续型的关节结构和偏低的重心帮助其适应多样性的环境。
Wright等[3]设计了一种仿蛇机器人,通过模拟蛇的运动步态,其可以实现爬行、攀爬和滚动等多步态运动,并利用头部模块安装的高清摄像头执行侦察任务。McKenna等[4]设计了一种基于环形皮肤致动器的仿蛇机器人,其利用机器人整个皮肤表面提供连续推进力,可以显著的提高蛇形机器人在不同环境中的灵活性。Barry A.Trimmer[5]实验室研发的仿生毛虫机器人既可以以蠕虫形态爬行,还可以模仿出卡特彼勒的滚动。魏武等[6]设计一种仿蛇机器人,其采用正交关节的模块化方式连接,可通过电机的驱动实现蜿蜒爬行、转向、抬头等多种运动方式。
仿蚕机器人是由多个关节模块组成的高冗余度系统,能够适应复杂多变的环境。本文对小型仿蚕机器人的关键组件—柔性腹节驱动器,进行了机械结构设计、转弯运动建模计算、仿真分析,并通过实验验证其合理性,为仿蚕机器人的柔性化研究奠定了基础。
1 蚕的生物特征与仿生结构设计
1.1 蚕的生物特征
蚕的身体形态如图1所示,生理特征参数如表1所示。蚕的头部引导自身运动;蚕的胸部辅助自身运动,且每个体节腹面有一对胸足,胸部各体节间无节间膜。蚕的腹部辅助自身运动,后半部分4个体节的腹面有四对腹足,腹部各体节间有节间膜。蚕的尾部作为自身运动的动力源,末尾体节的腹面有一对尾足,尾部各体节间有节间膜。
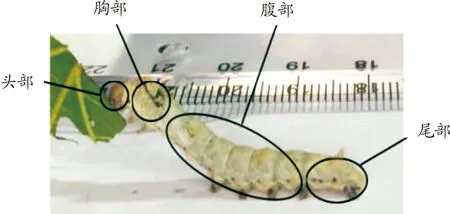
图1 蚕的身体形态示意图

表1 蚕的生理特征参数
蚕依靠胸部与腹部连接之间无腹足的柔性腹节单侧肌肉的收缩与伸展来完成转弯动作,如图2所示。蚕腹部各体节间有节间膜,但柔性腹节处无腹足,且相比于其他关节,运动变形较大且灵活,具有分布式连续变形的能力。

图2 蚕的转弯运动示意图
1.2 柔性腹节驱动器的结构设计
根据蚕的生物结构和转弯运动特点进行机构简化,采用模块化设计[7]。的仿蚕机器人的整体结构模型如图3所示,基本分为头部,腹部、尾部3个部分,其中头部主要起导向作用,腹部作为转弯运动动力源,尾部作为蠕动运动动力源。仿蚕机器人全长720 mm,宽56 mm,每节体节长约61 mm,共由11节组成,各体节之间采取正交连接的方式,构成4个正交模块,每个正交模块中由俯仰关节和偏航关节组成,俯仰关节完成蠕动动作,偏航关节完成转弯动作。

图3 仿蚕机器人整体结构示意图
为实现仿蚕机器人转弯关节的柔性化,增强其环境适应能力[8],基于蚕腹部前半部分的结构特点和运动特性设计柔性腹节驱动器,如图3中转弯关节所示。柔性腹节驱动器是一种差动式的关节驱动器[9],如图4(a)所示,分别进行两侧气囊的充气,将单侧气囊输出的直线位移转换成关节的角位移,从而实现往复的摆动运动。

图4 驱动器工作原理及数学模型
如图4(b)所示,柔性腹节驱动器中单个刚体连杆的长度为l,气囊偏心距为a,假设单侧气囊伸长的长度为X时,驱动器的转动角度为θ。
连杆转角α=π-θ/2,气囊弯曲角度β=π/2-α=θ/2,则气囊的伸长长度为
(1)
气囊的形变量为
(2)
通过MATLAB对式(2)进行计算,得到气囊形变量与其弯曲角度的关系如图5所示,可以看出气囊的有效转弯角度为45°,最大伸长量为7.7 mm。
柔性腹节驱动器的主体是由两个硅橡胶制作的气囊组成,气囊由圆柱形的气囊空腔和菱形固定支架组成[10],气囊的结构设计如图6所示。气囊整体长度为54 mm,内壁直径为6 mm,壁厚为3 mm,两侧的菱形支架安装在驱动器的支撑架上。当进行转弯运动时,气囊充气后开始膨胀发生轴向和径向位移,但由于固定支架的限制,径向位移对运动几乎没有影响,可以忽略不计,主要利用其轴向上的位移。
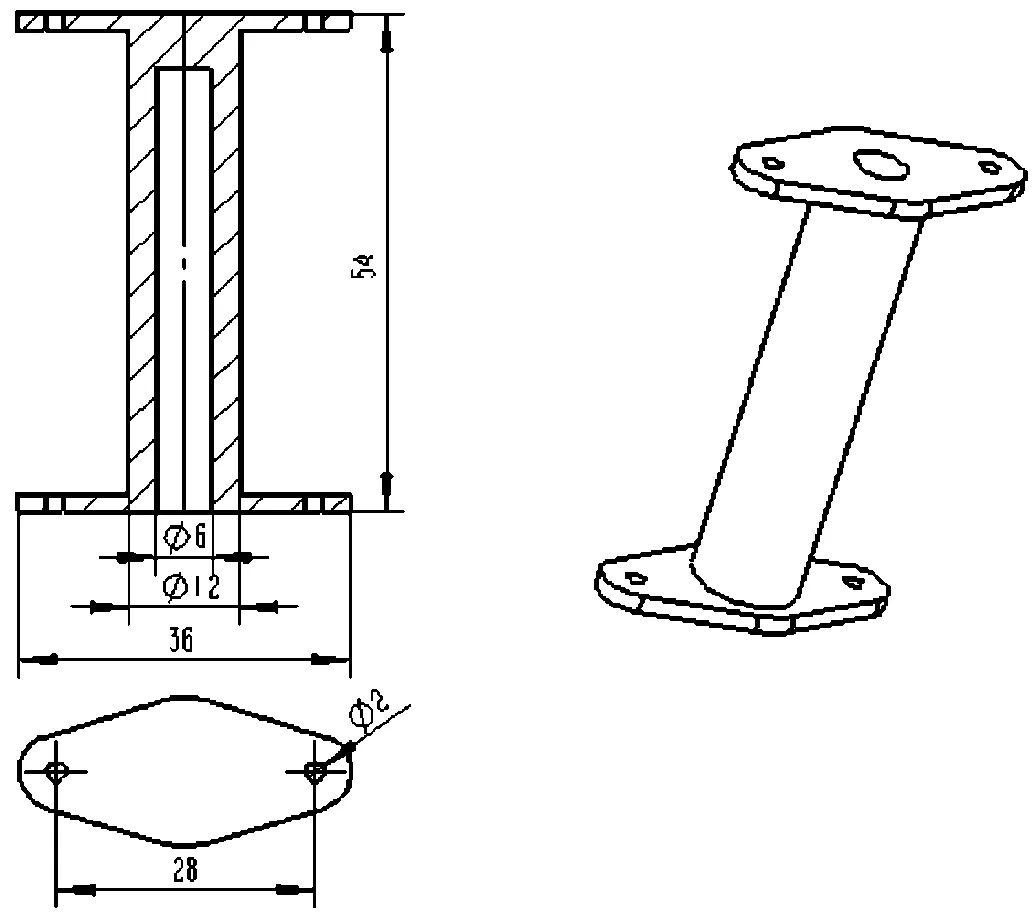
图6 气囊结构
2 仿蚕机器人转弯运动建模与仿真
2.1 转弯运动曲线及其规划
为了方便建立仿蚕机器人转弯运动模型,将其简化为二维平面连杆系统,用连杆形成的运动波来模拟机器人的转弯运动[11]。当仿蚕机器人进行转弯运动时,以转弯关节运动导向为主,偏航关节的转动为辅。含有柔性腹节驱动器的转弯关节的转角变化规律如下:
φ(t)=Asin(ωt+λ)
(3)
式中:A为幅值参数;ω为转动角频率;λ为偏转参数。
偏航关节的转角变化规律可以采用Serpenoid曲线[12]来规划辅助转弯运动轨迹,可以参考Serpenoid曲线对偏航关节的转弯运动进行规划[13]。
(4)
首先将Serpenoid曲线的曲率方程进行简化[14]
ρ(s)=-absin(bs)+c
(5)
对式(5)进行积分运算,得到夹角θ(s)
θ(s)=acos(bs)+cs
(6)
为了方便得到仿蚕机器人的转弯运动方程,将其简化为N节平面连杆,当连杆长l足够小时,连杆连接就可以近似为光滑的转弯曲线,对于仿蚕机器人的N节连杆,其关节转角即为弧长s=0,l,2l,…处的夹角。经过计算,最后得到弧长s=ct,ct+l,ct+2l,…的关节转角函数为
φi(t)=αsin(ωt+(i-1)β)+γ
(7)
其中:α为转弯曲线的初始角度,主要影响曲线的幅值,β决定关节间的相位差,主要影响运动曲线中包含波的数目,ω决定转角频率,主要影响曲线周期。
为了提高转弯运动控制函数基于仿蚕机器人转弯运动的实际应用性,通过单位阶跃函数g(t)=1-e-λt对其进行优化,使信号更加平滑地进入系统。g(t)函数的曲线如图7所示,令λ分别取值为0.5、1、2、3,从其中可以看出,λ数值越大,函数增长越快,响应时间越短。因此可以使用该函数对转弯运动控制函数进行优化,优化后的函数如式(8)所示。
φ(i)=(1-e-λt)(asin(ωt+(i-1)β)+γ)
(8)

图7 λ参数对单位阶跃函数的影响曲线
取参数a=π/6,β=0.6π,ω=2,γ=0,然后分别取λ=0.5、1、2、3,根据式(8)可得偏航关节在不同值下的角度变化曲线,如图8所示,数值越大,函数到达期望角度越快,通过g(t)函数优化的意义是希望角度可以平滑地从0增长到期望值,从而保证转弯运动控制函数的实用性和稳定性,因此选取λ=0.5作为函数参数。

图8 λ参数对转弯运动控制函数的影响曲线
最后,得到仿蚕机器人转弯运动控制函数如式(9)所示,i=1时,表示的转弯关节,i=2、3、4时,表示的是偏航关节。

(9)
2.2 转弯运动分析与仿真
为了验证基于柔性腹节驱动器建立的转弯运动控制函数的可行性,对仿蚕机器人进行基于ADAMS转弯步态仿真。
在上面小节,建立了转弯运动控制函数,其中,参数γ影响的是转弯运动的方向。此时,偏航关节起辅助转弯运动的作用,其运动轨迹不发生偏转,因此γ=0。仿蚕机器人的转弯运动控制函数如下所示。

(10)
在ADAMS中搭建仿真平台,根据期望的转弯角度,取a=π/6,β=0.6π,ω=2,λ=0.5。设置仿真时长为40 s。仿蚕机器人右转弯运动仿真过程如图9所示。

图9 一个周期的转弯运动仿真过程示意图
其中参数ω主要影响的是转弯运动的周期,α影响曲线的幅值,β决定关节间的相位差,从而影响转弯运动的速度。通过仿真分析,得到小型仿蚕机器人转弯运动时的偏航关节的角度变化的关系,如图10所示。
仿蚕机器人头部在x轴方向的角度变化如图11所示,从图11中可以看出含柔性腹节的仿蚕机器人在转弯运动开始时,头部转角有轻微抖动,但逐渐趋于平缓,直至达到稳定状态。由此可以证明依靠头部进行导向运动,偏航关节进行辅助运动的转弯模型,可以使仿蚕机器人的转弯运动趋于平滑稳定。
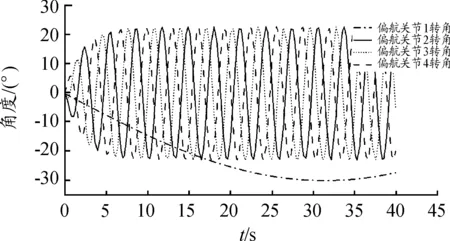
图10 关节角度变化图

图11 转弯角度变化曲线
3 基于ADAMS和MATLAB的转弯关节联合仿真
由于存在柔性腹节驱动器自身的非线性特性和气泵电磁阀开关操作延迟的影响,会导致仿蚕机器人在进行转弯运动时关节摆角出现累计偏差,致使关节摆角脱离期望的运动轨迹,因此,通过ADAMS和MATLAB联合仿真技术,运用数字PID控制方法,解决这一非线性问题。
3.1 联合仿真虚拟样机系统的设计
通过基于ADAMS和MATLAB的转弯关节联合仿真,主要分为4个步骤,如图12所示。

图12 联合仿真流程框图
首先建立仿蚕机器人机械结构的虚拟样机模型,定义各模块构件间的约束和驱动相关属性,添加合适的分量力矩;然后在MATLAB中设计并搭建仿蚕机器人进行转弯运动的控制方案;最后进行仿真和调试,通过设置数据交换时间间隔、仿真时间和步长,最终得到关节角度变化曲线图。
3.2 基于PID控制算法的控制器设计
仿蚕机器人的转弯关节的PID控制器是以数字式PID控制算法为理论基础,在控制程序中,其入口参数为期望角度值和实际角度值,期望角度就是控制给出的角度值,反馈角度是传感器测得的驱动器的转弯角度[15]。
如图13所示,上位机设置期望角度,测量角度来自MPU6050,期望角度减去测量角度得到偏差角度,角度环的输入为偏差角度值,经过角度环PID后输出期望的角速度[16],更新周期100 Hz。

图13 PID算法流程框图
根据含有柔性腹节的仿蚕机器人转弯运动模型,在MATLAB/Simulink中建立仿蚕机器人转弯关节的PID控制器的仿真模型。
3.3 联合仿真结果分析
基于ADAMS和MATLAB的联合仿真方法对仿蚕机器人柔性腹节的转弯运动摆角偏差进行修正,并对摆角进行实时跟踪与控制。在仿真的过程中,根据PID控制器的调参公式不断修改控制器的3个参数,直到角度变化的轨迹为比较理想的曲线。
设置仿真时间为6 s,摆角的期望值为20°,多次调整3个参数后得到较为理想的转弯运动摆角曲线如图14。

图14 角度跟踪曲线
当比例环节系数KP=0.023、积分环节系数KI=0.041、微分环节系数KD=1时,可以得到较为理想的角度变化轨迹曲线,角度过渡平缓,稳定性好。
4 转弯运动试验
对仿蚕机器人进行零部件安装与调试,仿蚕机器人初始状态如图15(a)所示,左转弯效果如图15(b)所示,右转弯过程如图15(c)所示。
转弯运动的仿真结果与机器人样机的试验结果如图16所示,其中两条曲线分别表示在转弯运动仿真与机器人样机试验中机器人头部在x轴方向的角度变化。从图16中可以看出,给定的预期转弯角度为16°,实际转弯角度达到了15°,经过ADAMS和MATLAB转弯关节的联合仿真,由于引入了PID控制算法,在进行转弯运动时,头部的转弯角度在起始位置运动比较稳定,然后慢慢稳定的平滑转动到期望转弯角度,满足本项目要求仿蚕机器人转弯运动自然、过渡柔顺化的要求,试验结果基本符合预期。

图15 左右转弯效果图

图16 转弯角度曲线
5 结论
1) 建立了仿蚕机器人简化连杆转弯运动模型及其转弯运动模型控制函数,通过ADAMS仿真验证了转弯运动模型的合理性及其控制函数的实应性。
2) 通过样机试验了仿蚕机器人的转弯运动控制模型,验证了柔性腹节驱动器设计的可行性,对仿蚕机器人的柔性化研究具有重要参考价值。

