中介轴承游隙和刚度对双转子系统非线性特性的影响

贾 延，刘永葆，王 强，李 默，李 俊

(海军工程大学 动力工程学院， 武汉 430033)

燃气轮机由于转速高、功率大、结构复杂等特点，振动问题一直以来都是其安全稳定运行的重要因素。轴承作为燃机的重要支承零件，其本身具有复杂的非线性特征(如径向游隙、Hertz接触力和接触刚度等)。针对轴承-转子系统，国内外学者做了一系列的研究。文献[1]利用拉格朗日方程，建立了有限元模型，分析了转子系统动力学行为；文献[2]考虑一种球轴承刚性转子系统，通过数值仿真计算，研究轴承表面波纹度对转子的振动影响；文献[3]建立含横向裂纹的双跨度转子模型，分析了裂纹扩展、裂纹角和滚动轴承径向间隙对系统响应的影响；文献[4]推导了轴承工作状态下的轴承力，研究表明非线性轴承力会诱发变刚度振动；文献[5]建立高速滚动轴承-转子系统动力学方程，分析转速和阻尼参数对系统的非线性振动影响规律；文献[6]建立滚动轴承-转子系统模型，分析游隙和不平衡力对系统响应的影响；文献[7]研究了中介轴承波纹度对双转子系统的动力学特性产生的影响；文献[8]建立了含滚动轴承径向游隙的整机振动模型，分析不同转速下机匣响应特征及游隙对接触力的影响；文献[9]以磁悬浮轴承支承的航空发动机高压模拟转子为对象，分析磁悬浮轴承的控制参数对系统动力学响应的影响；文献[10]介绍了一种游隙可调的轴承结构及工作原理，分析了游隙对转子系统振动的影响；文献[11]研究了在涡轮机和发电机的细长转子系统中存在的Hopf分叉的类型，发现较高的基座质量和阻尼会产生超临界分叉；文献[12]分析轴承等效刚度、轴承游隙与线性阻尼系数对转子系统滞后突跳的影响；文献[13]分析了机动载荷、偏心对转子系统非线性振动及分岔特性的影响；文献[14]考虑中介轴承外圈早期剥落故障模型，通过数值积分方法获取故障激励下的整机振动响应。文献[15]建立三自由度分段非线性轴承故障碰撞模型，研究了滚动体与内圈缺陷的碰撞冲击而出现的Neimark-Sacker分岔等非线性行为。文献[16]、文献[17]建立了三支承双跨转子-轴承系统，考虑轴承的非线性，分析转速和径向游隙对系统非线性动力学的影响。

上述研究缺少了针对燃气轮机双转子系统的非线性特性研究，因此本文根据某型燃气轮机的实际结构，建立非对称支承的三盘转子模型。改变中介轴承的游隙、接触刚度的值，根据系统的全局分岔图，可以看到系统分岔混沌点的位置，为确定中介轴承游隙和接触刚度的选择范围，提供一定的理论依据。

1 系统动力学建模

本文以某型船用燃气轮机为基础，通过集中质量对其结构进行简化得到双转子系统模型，如图1所示。转轴假设为无质量的弹性轴，只考虑转子的横向振动，忽略扭转振动和轴向振动，即每个集中质量处考虑x、y方向的自由度。Ob1、Ob2、Ob3、Ob4分别为轴承1、轴承2、轴承3、轴承4的形心，Op1、Op2、Op3分别为盘1、盘2、盘3的形心，Oc1、Oc2、Oc3分别为盘1、盘2、盘3的质心，e1、e2、e3分别为盘1、盘2、盘3的偏心量。假设转轴1和转轴2的结构材料相同，根据平面梁结构关系得到各个轴段间的刚度关系，k1=k/125，k2=4k，k5=k/2，k3=k4=k6=k。

图1 某型燃气轮机双转子系统模型示意图

本文所建的模型船用燃气轮机双转子系统动力学模型，共有7个集中质量。模型共14个自由度，根据Lagrange运动方程得到系统非线性动力学微分方程组为

M=diag(mb1，mb2，mp1，mb3，mb4，mp2，mp3)

C=diag(cb1，cb2，cp1，cb3，cb4，cp2，cp3)

(1)

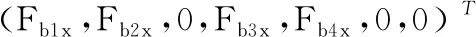
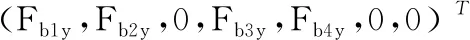
式中：M为系统质量矩阵；C为系统阻尼矩阵；K为系统刚度矩阵；Fbx、Fby为轴承力矩阵；Fex、Fey为转子不平衡力矩阵。其中ω1是转子1的转速，ω2是转子2的转速，转速比α=ω2/ω1。

本文忽略了轴承的油膜力对系统的影响，根据Hertz接触理论，考虑以轴承滚动体与滚道的弹性接触力来体现轴承非线性力对系统的影响。图2所示为滚动轴承模型，Ri是轴承的内径，Ro是轴承的外径，Gr表示轴承的径向游隙。

图2 滚动轴承模型示意图

对方程组进行无量纲化处理，ξ是无量纲长度参考值，引入无量纲参数：

(2)

对于滚珠轴承h=1/2；对于圆柱滚子轴承h=1/9。其中滚动轴承非线性轴承力无量纲化后得到无量纲公式如下：

(3)

对于滚动轴承1、4，n=3/2；对于圆柱滚子轴承2、3，n=10/9。轴承1、轴承2、轴承3、轴承4的位置如图2所示。

根据无量纲参数(2)、(3)和方程组(1)，得到无量纲方程组(4)，如下：

(4)

系统动力学微分方程中各符号的单位及意义如表1所示。中介轴承的参数：外径Ro=47 mm，内径Ri=25 mm，滚动体个数Z=15，接触刚度Kb=3×109N/m3/2，游隙Gr=12 μm。内圈转速ω1， 外圈转速ω2。

表1 微分方程中符号的单位及意义

2 中介轴承径向游隙对系统非线性动力学特性影响

径向游隙是轴承设计时的重要参数，也是轴承非线性的重要因素之一，对于轴承及转子系统的安全稳定运行有重要意义。根据Hertz接触理论，轴承力的非线性体现为轴承的载荷-变形指数和力的分段性，而径向游隙决定着轴承力的分段性。因此，本节研究中介轴承的径向游隙对系统非线性动力学影响规律。

以盘2的非线性特性体现系统的振动特性，中介轴承径向游隙在0～50 μm之间变化，盘2的水平位移Xp2随着游隙变化的分岔图如图3。从图中可以看出，盘2的非线性特性发生明显变化。选取一些固定游隙值进行分析。

当中介轴承游隙Gr=5 μm时，如图4，盘2的相图中有2个交错的圆环，庞加莱截面图上有2个独立的点，频谱图中转频为主，还出现了1/2分频，说明盘2通过倍化分岔进入了周期二运动状态。 当中介轴承游隙Gr=15 μm时，如图5，盘2的相图呈现出轮胎状的圆环，庞加莱截面图近似一个封闭的圆，频谱图中转频为主，还出现了1/2分频和一些连续的分数频，说明盘2发生了Hopf分岔，处于拟周期运动状态。当中介轴承游隙Gr=40 μm时，如图6，盘2的相图中有一个圆环，庞加莱截面图上近似看作有一个独立的点，频谱图中转频为主要频率成分，说明盘2进入了拟周期运动状态。

图3 Xp2随中介轴承径向游隙变化的分岔图

图4 中介轴承游隙为10 μm的相图、庞加莱截面图和频谱图

图5 中介轴承游隙为15 μm的相图、庞加莱截面图和频谱图

图6 中介轴承游隙为40 μm的相图、庞加莱截面图和频谱图

3 中介轴承接触刚度对系统非线性动力学特性影响

滚动轴承刚度的确定是转子系统振动性能分析的基础。目前，对于滚动轴承刚度的计算，主要基于静力学法、基于拟静力学法和基于拟动力学法3种方法。拟动力学法充分考虑了转速等影响刚度值的因素，但其对初值选取要求高，求解时不易收敛。因此本文忽略了轴承刚度值的求解过程，直接给出刚度的变化范围。同时忽略径向游隙对刚度的交叉影响，在保持其他参数不变的情况下，只改变单一参数研究系统的非线性特性响应。本节刚度变化范围设定为1×107N/m3/2至1×1010N/m3/2，盘2水平位移Xp2随中介轴承刚度变化的分岔图如图7，可以看出系统通过倍周期分岔进入了混沌状态。具体选取接触刚度值，来分析系统非线性动力学特性。

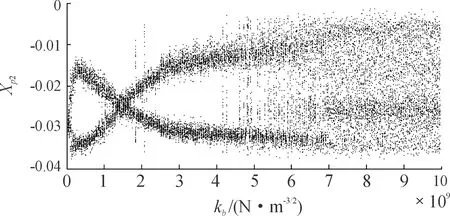
图7 Xp2随中介轴承接触刚度变化的分岔图

当中介轴承刚度kb=1×107N/m3/2时，如图8，盘2的相图中有一个圆环，庞家来截面上可近似看作一个点，频谱图中以主频为主，说明盘2处于拟周期运动状态。当中介轴承刚度kb=1×109N/m3/2时，如图9，盘2的相图中出现了2个相互交错的圆，庞家来截面上有2个孤立的点，频谱图中以主频和1/2分频为主，说明盘2通过倍化分岔进入周期二运动。当中介轴承刚度kb=1×1010N/m3/2时，如图10，盘2的相图中是相互交错没有规则的线，庞家来截面上是一些散乱的点，频谱图中以主频为主，还出现一些分数频，说明盘2处于混沌状态。

图8 中介轴承接触刚度为1×107 N/m3/2的相图、庞加莱截面图和频谱图

图9 中介轴承接触刚度为1×109 N/m3/2的相图、庞加莱截面图和频谱图

图10 中介轴承接触刚度为1×1010 N/m3/2的相图、庞加莱截面图和频谱图

4 结论

1) 径向游隙较小时，系统处于周期运动状态，随着游隙增大，系统通过倍化分岔进入周期二运动；游隙继续增大，系统发生了Hopf分岔，最后稳定在拟周期运动。当游隙过大时，轴承接触力较小甚至为零，降低了系统非线性因素的作用，使得系统非线性行为减少。

2) 接触刚度较小时，系统处于周期运动状态；刚度增大，系统通过倍化分岔从拟周期状态进入周期二运动；刚度继续增大，系统进入了混沌域。随着接触刚度的增大，轴承非线性接触力增大，增强了系统的非线性特性。