基于偏振光的干涉测长法

胡婷婷，杜玉娴，白在桥

(北京师范大学 物理学系，北京 100875)

利用光的干涉测量微小位移或光程差是一类重要的大学物理实验. 常见的实验包括利用迈克耳孙干涉仪测量空气折射率、薄膜折射率或厚度、金属弹性模量/线胀系数、材料的电/磁致伸长系数等[1-7]. 实验中通常是通过数条纹的数量来确定动镜位移或其他因素导致的光程差. 数条纹虽然操作简便，但也存在一些问题，比如：

1)只适合位移缓慢变化的情况. 如果位移变化过快，人眼会看不清条纹的结构；

2)只适合位移(光程差)单方向运动的情况. 如果位移方向不固定，条纹既有涌出也有陷入，人工计数将变得十分困难；

3)读数限定为半波长的整数倍. 为保证测量精度，一般需要几十甚至上百个条纹，不适合测量波长或亚波长范围的位移量.

前2个问题可以用(单向或可逆)自动条纹计数器解决[8-12]. 但为了解决第3个问题，必须采用比数条纹更精细的方法.

1 实验原理

光强分别为I1和I2的2束光的干涉光强为

(1)

其中相位差Δφ直接与位移相关. 测出I1,I2和I，就可以根据(1)式算出cos Δφ. 不过在1个周期内cos Δφ与Δφ是一对二的关系，除非已知位移的运动规律(比如匀速运动)，一般情况下并不能由干涉光强推知位移的变化情况. 本文针对此问题，利用光的偏振自由度，无需对位移的变化方式做任何假设，即可以测出干涉相位，从而可以稳定地实现位移的连续测量.

1.1 原理图与基本思路

光路如图1所示，在传统迈克耳孙干涉仪光路(虚线框)的基础上做了改进：

1)激光入射分束镜(BS1)之前先经过1块偏振片(P)和1块分束镜(BS0)；

2)激光从干涉仪出射后经过1块偏振分束镜(PBS)；

3)使用3个光电探测器分别(D0,Dp,Ds)测量从BS0分出的光强I0和从PBS出射的2路光强Ip0和Is0.

偏振片的透振方向与水平方向大致成45°，这样入射光中p分量和s分量比例固定，基本为1∶1. BS0和光探测器D0的作用是监视入射光强. 相对光强为

(2)

结果将不受激光器输出状态漂移的影响.

图1 测量原理图

由于p光和s光之间不会产生干涉，所以干涉仪中同时存在2套干涉光路，它们在空间上完全重合，直至PBS把它们分开，进入对应的探测器. 因此有

(3)

相位差来自干涉仪两臂的光程差和光学元件导致的光程差，即

(4)

式中λ为激光波长，ΔL为干涉仪两臂的光程差，Δφp0与Δφs0分别为光学元件对p光和s光引入的相位差. 由于分束镜镀膜对光的反射与透射都依赖于光的偏振状态，一般Δφp0≠Δφs0. 因此，当ΔL改变时，Ip和Is的变化有固定的相位差δ0≡Δφp0-Δφs0. 只要δ0不等于π的整数倍，(Ip,Is)就会在固定的椭圆上移动. 记录测量点在椭圆上的运动轨迹，就可推知ΔL如何随时间变化，这就是本文测量方法的基本思路. 虽然原则上只需要δ0≠kπ，但如果δ0过于接近kπ，椭圆就变得很扁长，测量结果就会因噪声的影响变得不稳定. 在本文的实验装置中δ0大致为45°，为降低噪声的影响. 如果条件允许，可在干涉光路的1条臂中插入可调相位延迟片，即可对δ0进行调节.

1.2 计算方法

根据(3)式和(4)式，不妨设

(5)

经过仿射(平移加线性)变换：

(6)

有

(7)

(Ip′,Is′)在单位圆上,而且辐角随光程差均匀变化，光程差改变λ，(Ip′,Is′)在单位圆上运动1周. 如果采样率足够高或者光程差变化足够慢，可以保证前后2个采样点之间的光程差改变量小于λ/2，那么就可以通过连续跟踪，得到光程差随时间的变化曲线.

ΔL很可能不随时间匀速变化，因此一般不能通过正弦曲线拟合得到Ap,Bp,As,Bs与δ0. 下面给出根据数据点的几何性质(即它们位于个椭圆上)，来拟合这5个参量的方法. 平面上椭圆的一般方程为

(8)

其中a,b,c,d,e,f为常数，而且矩阵

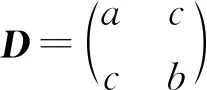
(9)

是正定的. 方程(8)可写成XTP=0，其中向量X和P定义为

(10)

设测量点的集合为{(Ipi,Isi)|i=1,2,…,N}. 由于存在测量误差，一般并不存在1个向量P与所有的Xi都正交. 对所有实测数据点求和，得到对称矩阵

(11)

然后用M的最小特征值对应的特征向量作为对P的估计. 由于特征向量可以相差常数因子，这里要求a>0. 由于D是正定的，同时一定有b>0和ab-c2>0.

a,b,c,d,e,f确定后，就可以计算Ap,Bp,As,Bs与δ0了. 首先，(Ap,As)为椭圆的中心,可表示为

(12)

(Bp,Bs)可根据下式计算

(13)

其中

(14)

最后，相位差δ0可根据下式计算

(15)

由于三角函数的特性，可以得到4种不同的仿射变换(分别对应δ0→±δ0,2π±δ0). 实验中固定选择1种即可.

利用上述方法得到仿射变换的参量，将数据点映射到单位圆上. 计算辐角(即相位)，并根据前一时刻的值,通过适当平移2kπ，把辐角连续地映射在实轴上. 最后乘以λ/2π(或者λ/4π)得到光程差ΔL(或反射镜相对位移S)的变化曲线.

2 装置与方法

实验装置以Thorlabs公司的迈克耳孙干涉仪教学套装为基础搭建，实物如图2所示. 光源采用氦氖激光器(λ=632.8 nm,功率1.5 mW). 干涉仪的反射镜M1固定在二维调整架上，反射镜M2固定在待测金属杆的前端，金属杆的尾部通过连接杆用螺丝固定在光学面包板上. 金属杆外面包裹加热箔，可通过电流改变金属杆的温度. 金属杆的对称轴上钻有1个深孔，可以将温度传感器(K型温差电偶)插入，测量金属杆的温度. 偏振分束镜使用Thorlabs PBS201. 3个光电探测器均为硅光电二极管(Thorlabs DET36A2). 探测器输出至数据采集卡(NI USB-6212). 由于D0探测的光信号变化缓慢，所以采用了较大的耦合电阻(10 kΩ)，为了提高响应速度，Ds和Dp使用了较小的耦合电阻(1 kΩ). 因此Is和Ip要比I0小1个数量级. 所有元件，除了激光器和偏振片，都固定在30 cm×45 cm光学面包板上，整体放在光学平台上.

装置的调节方法与通常的迈克耳孙干涉仪相同. 为观察调节效果，需要在激光器输出位置插入扩束镜，并用白屏观察干涉图样. 要求两臂的光程尽量相等，使干涉图样的中心斑点远大于探测器的有效接收区域(2.2 mm×2.2 mm). 测量时取走扩束镜，让光直接打在探测器上.

1.He-Ne激光器 2.偏振片 3.分束镜(非偏振) 4.反射镜M1 5.反射镜M2 6.PBS 7.探测器图2 装置照片

利用此装置可完成以下2个实验：

a.测量系统的冲击响应. 轻微敲击光学面包板，干涉条纹出现晃动，然后逐步平稳. 编写LabVIEW程序，当监测到振动(干涉光强发生剧烈变化)后，记录1 s的数据(采样率105s-1). 用全部的测量数据拟合椭圆参量，确定仿射变换，对光强进行变换，计算辐角，得到光程差的变化曲线.

b.测量金属的线胀系数. 加热金属杆使其长度发生改变，M2发生位移，引起干涉条纹移动. 实验所用数字温度计可将温度按1 mV/℃的格式转换成电压输出. 利用数字万用表(Rigol DM3058E)测量输出电压，并且编程通过VISA自动读取测量结果. 直流电源(Rigol DP1116A)也可以通过VISA控制. 程序控制加热温度超过TH=36 ℃就断电，冷却到温度低于TL=31 ℃就通电加热(加热电流0.3 A). 可尽量减小人为操作失误和读数误差，便于验证测量结果的可重复性. 金属杆升温和降温的时间都较长(大约5 min)，光程差变化较平缓. 实验需要接近实时地显示金属杆的长度变化，实验中每秒采集1 000组光强数据(采样率103s-1)，这些数据对应的光程差变化不大，不能形成完整的椭圆. 因此保存30 s的光强数据(每次采集到新数据后都需要更新)，用所有数据拟合椭圆，确定仿射变换参量，并且把当前1 s的数据转换成杆的伸长量.

3 结果与分析

3.1 冲击响应测量

图3为1次采集到的光强波形. 可以看出光强变化相当剧烈. 在前面一段时间(大致0～0.6 s)，光强变化的最大值与最小值基本固定，对应光程差的变化幅度大于λ，有超过1个条纹的吞吐. 之后光强的极值随时间改变，对应光程差的变化幅度小于λ，变化小于1个完整的条纹.

图3 不同偏振相对干涉光强随时间变化曲线

图4给出了其中一部分的放大. 注意图中标出的9个光强的极大值，其中1，3，5，7，9号Ip和Is看起来是同相位的，而2，4，6，8号Ip和Is有明显的相位差. 前一组极大值对应光程差的极值(即反射镜振动位移到极值处)，这对p光和s光没有差别. 而后一组极值对应光程差达到为λ的整数倍，与偏振方向有关，所以Ip和Is有明显的相位差.

图4 图3波形的细节放大

将(Ip,Is)数据按xy方式绘图，得到图5. 虽然存在较大的噪声，但数据点形成了很明显的椭圆(图中红色为拟合椭圆). 注意Ip和Is的数值越大，噪声也越大. 用数据拟合椭圆，并用所得的仿射变换作用于原始数据，结果见图6. 可以看出(Ip′,Is′)都在单位圆(红色曲线)附近. 虽然结果同样存在较大的噪声，但数据距离原点都足够远，辐角的计算是可靠的.

将辐角折合成为反射镜的相对位移，得到振动波形，结果见图7. 图中可以看到明显的振动衰减过程. 放大对应图4的部分(见图8)，可见清晰的正弦振动. 注意图中的各位移极值点，它们与图4中的1，3，5，7，9号极值对应. 而且噪声水平明显小于图4中的光强信号. 噪声减小的原因是Ip和Is的噪声存在显著的正向关联，因此噪声主要影响数据点到原点的距离，而对辐角的影响相对较小.

图5 在(Ip,Is)平面显示数据

图6 经过仿射变换后的数据

图7 系统振动衰减曲线

图7中的衰减曲线存在明显的拍，说明系统存在2个相差不大的固有频率. 对衰减曲线做傅里叶变换，结果见图9. 从图中可得这2个固有频率分别为206 Hz和224 Hz. 此外，系统还存在260 Hz，398 Hz，484 Hz等固有频率.

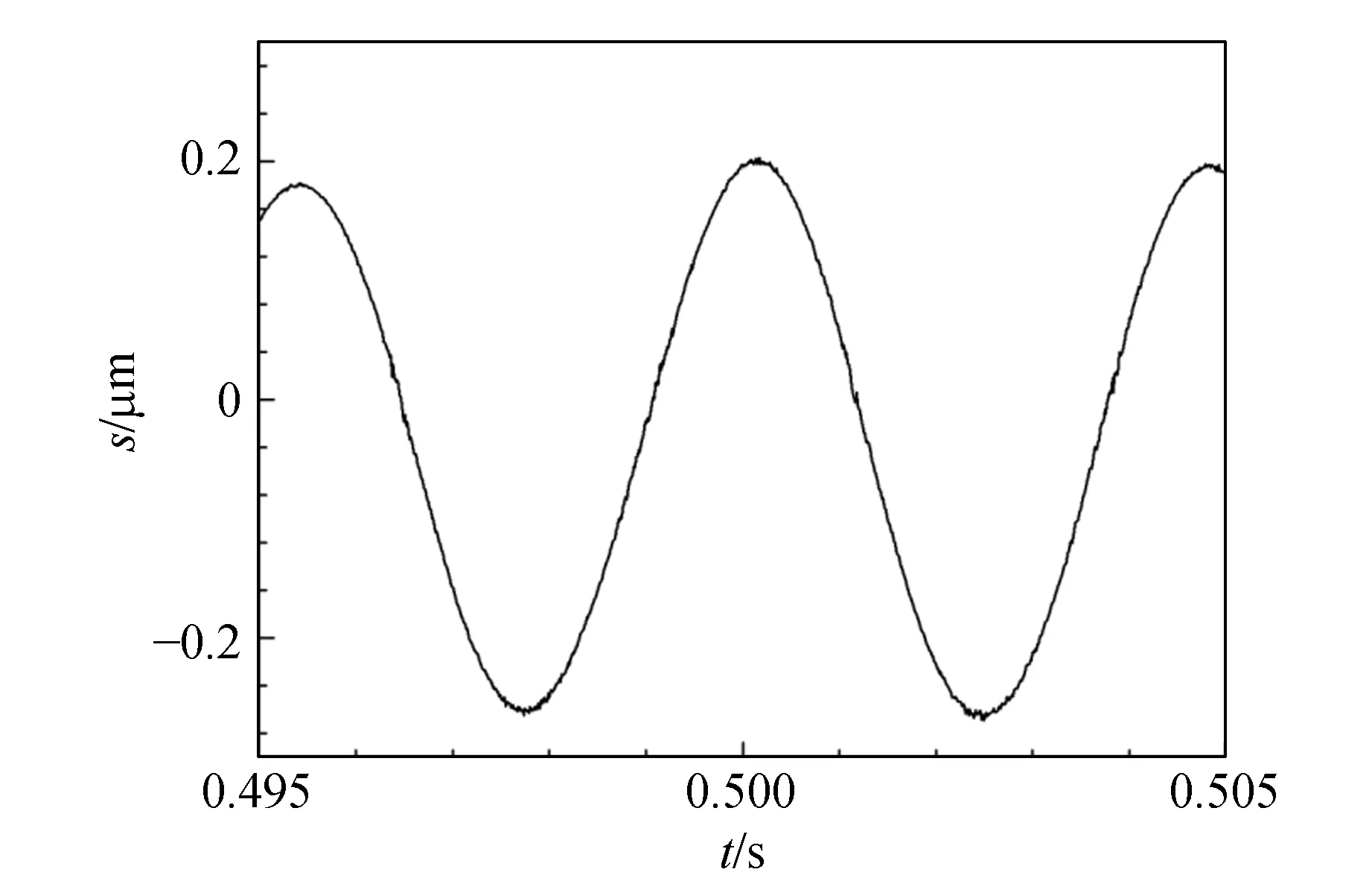
图8 衰减曲线细节放大

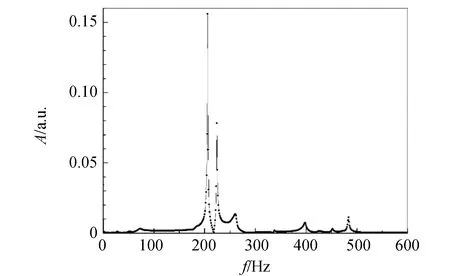
图9 衰减曲线的频谱

进行多次测量，每次敲击光学面包板的位置或力度不相同. 表1为21次测量所得各个参量拟合值的平均值值与标准差. 可以发现Ap,Bp,As和Bs拟合值的相对标准偏差都小于0.1%，δ0的标准偏差只有0.002 drad≈0.12°，这说明实验光路、探测系统和数据处理算法的稳定性很好.

表1 拟合参量统计

3.2 金属线胀系数测量

图10显示了连续4 000 s的测量数据，图10(a)每个点是1 s内1 000次杆伸长量的平均值，图10(b)是从数字万用表读出的温度值. 图中可见有7次完整的升温和冷却过程. 伸长量δL和温度T的变化形式都类似电容充放电. 这是因为温度越高，散热越快，导致加热段升温和冷却段降温都越来越慢.

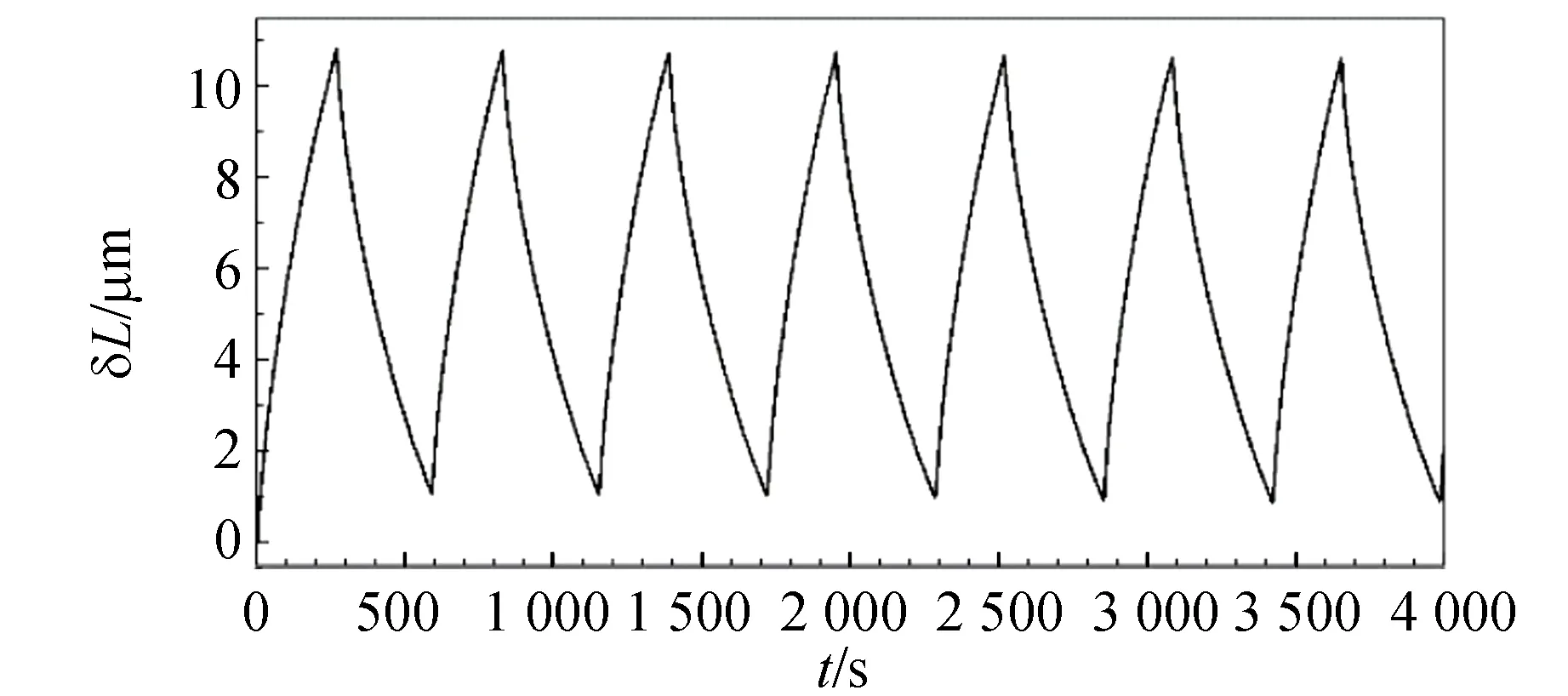
(a)

(b)图10 金属杆伸长量δL与温度T随时间变化曲线

在(T,δL)平面中画出测量数据，结果见图11. 图中可以看出在升温段和冷却段，δL都与T呈很好的直线关系. 但这两段明显不重合，T的变化落后于δL，表现为滞回性. 可理解为：δL反映了杆平均温度的改变，温度探头测量的是金属杆内部的温度，但加热和散热都发生在金属杆的表面，因此T的变化要滞后于δL.

图11 在(T，δL)平面显示测量数据

取T在31.5～35.5 ℃之间连续的升温或冷却阶段的数据. 这14段数据的线性相关性系数都大于0.999 93. 用最小二乘法计算δL对T变化的斜率κ=(1.880 5±0.007 8) μm/℃，结果见表2. 可看出升温段(奇数次)的斜率总体上略小于冷却段(偶数次)的斜率. 原因可能是升温段时间略短于冷却段，因此受滞回效应的影响会更大. 滞回效应总会导致测量斜率偏小，所以升温段的斜率比冷却段要小. 对拟合斜率取平均，并取等效杆长L=79 mm，计算铝的线胀系数，结果在参考值(2.1×10-5～2.4×10-5℃-1)范围之内.

表2 δL对T的斜率κ拟合值

上面测量结果最大的误差来源于等效杆长L的测量. 因为金属杆是通过连接杆用螺丝紧固在光学面包板上，不易确定后端的位置. 79 mm是从紧固螺丝与金属杆的接触点算起的，本身不便测量，误差也比较大. 不过这个问题与本文主旨无关. 重要的是采取本文的方法，可以对微小位移进行连续测量. 在持续超过1 h的时间内，结果具有很好的可重复性. 由于位移分辨率远大于数条纹的方式，这种方法不仅提高了探测灵敏度，同时也清晰地展示了一些有趣的物理过程或现象，比如杆的散热和温度非均匀分布.

4 讨 论

干涉法测量微小位移(光程差)本质上是测量2维向量(即干涉复振幅)的角度. 干涉光强对应的是该向量在1个方向上的投影. 有2个方向的投影就可以唯一地恢复出向量的角度. 可逆条纹计数器就是利用了此思想[10-12]：用光纤探头在不同空间位置测量干涉光强，得到有一定相位差(最好是π/2)的2个信号. 根据2个信号达到极值的时序可以判断条纹是吞进或吐出. 这个方法的缺点是需要使用扩束镜，而且2个光强取样点的相位很容易受到扰动，导致信号弱且重复性不好. 本文使用2个不同偏振状态的干涉光强，它们在空间完全重合，测量时也不需要扩束. 因此数据信噪比高，结果可重复性好. 经过适当的数学处理，可以实现位移(光程差)的连续测量.

根据图8中峰-峰值小于1个波长的正弦振动曲线估计，单次位移测量的误差应该比波长小2个数量级. 为了估计位移测量的分辨率，保持干涉仪不动，连续测量反射镜的相对位移(固定变换参量). 图12中展示了典型的结果. 可以看见测量结果存在持续的涨落. 涨落的低频分量来自不可控制的环境扰动导致的光程差漂移. 这部分反映的是反射镜实际的相对位移. 涨落的高频分量(即短时间的涨落)是由探测器和采集卡的噪声造成的，也与数据处理算法有关. 即便光程差严格固定不动，这部分高频噪声仍然存在，因此它决定了实际的位移测量分辨率. 把测量结果通过截止频率为20 Hz低通数字滤波器，得到其低频分量(图12中红色曲线). 用原始信号减去低频分量，得到高频分量. 图13为高频分量的统计直方图. 可以看出形式很接近高斯分布，而且绝大部分值在±0.004 μm之间. 事实上，实验发现高频分量的标准差在0.001～0.005 μm之间，与光强的噪声水平正相关. 如果用3倍的标准差作为位移测量分辨率，则结果在0.003～0.015 μm之间，比波长小2个数量级. 此处估算的是单次测量的分辨率. 如果位移变化缓慢，提高采样率，用多次采样取平均值，可以进一步提高位移测量的分辨率(不过这样会降低时间分辨率).

图12 一段反射镜相对位移测量波形(黑色)及其经过低通滤波后的波形(红色)

利用本文方法，还进行了音叉共振曲线测量、刚体摆的随机振动测量等实验. 该方法结合了光的干涉和偏振，并利用LabVIEW进行数据采集与处理(以及仪器控制),可以研究的物理问题也比较丰富，因此是很好的大学物理综合设计性实验的选题. 本文的实验装置可以根据实际情况进行简化. 比如用普通的分束镜和2块偏振片代替PBS；用示波器代替数据采集卡，在XY模式下观察测量点在椭圆上的运动实现条纹的可逆计数. 数据处理也可以根据具体情况做适当的简化. 比如在测量短时间过程时，可以忽略激光器输出状态的漂移，不做光强标度，从而省去第1个分束镜和探测器.

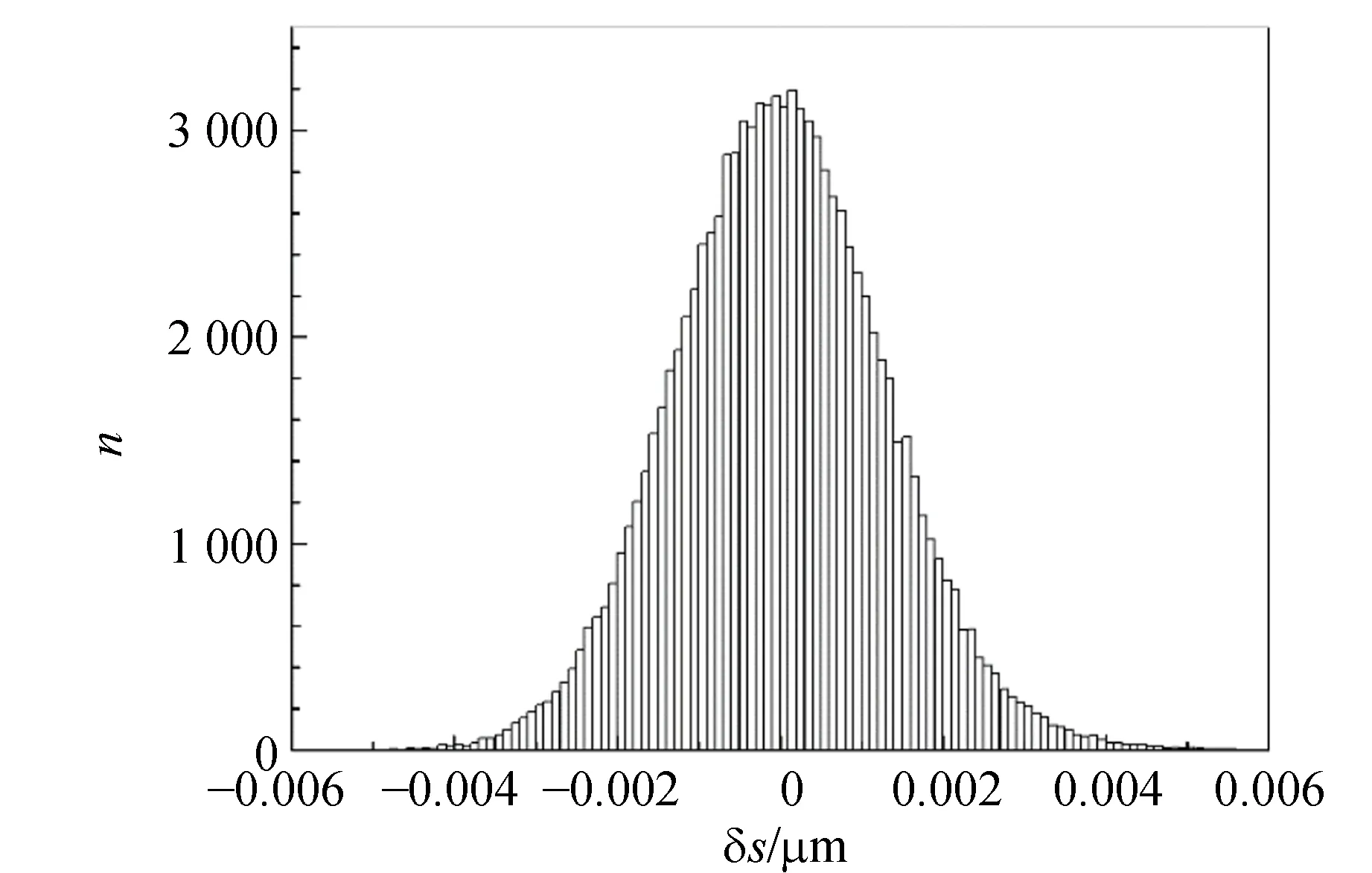
图13 位移测量噪声的统计直方图

致谢:感谢北京师范大学物理学系熊俊教授在本文写作过程提供的建设性意见.