非负矩阵Hadamard谱半径的新界值估计
李 华, 周树克,兰奇逊
(河南城建学院 数理学院,河南 平顶山 467036)
1 预备知识

设A=(aij),B=(bij)∈Rn×n,则C=A∘B=(aijbij)为矩阵A与B的Hadamard积。
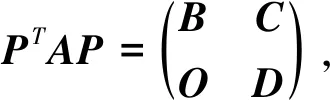
关于非负矩阵A,B的Hadamard积谱半径上界估计前人已经做了很多研究,文献[1]给出了一个经典的结果:
ρ(A∘B)≤ρ(A)ρ(B)
(1)
文献[2,3]也对类似问题做了很好的研究工作,给出了如下结果:

(2)

(3)
当矩阵A为非负矩阵,矩阵B为逆M-矩阵时,文献[4,5]给出了如下结果:

(4)

(5)
其中B-1=(wij)n×n.
本文对非负矩阵Hadamard谱半径估计继续做深入的研讨,得到新的估计式,估计式易于计算。
2 非负矩阵Hadamard积谱半径上界估计
设A=(aij)∈Cn×n,aii≠0,对任意i,j∈,有
引理1[6]设A=(aij)∈Rn×n是逆M-矩阵,则A≥0.
引理2[6]设A∈Zn,A是非奇异M-矩阵的充要条件是A的顺序主子式都是正的。
引理3[7]设A=(aij)∈Cn×n是严格按列对角占优矩阵,则A-1=(αij)存在,且对任意i∈N有
|αij|≤δj|αii|
引理4[8]设a=(a1,a2,…,an)T≥0,b=(b1,b2,…,bn)T≥0,则有:
引理5[9]设A=(aij)∈Cn×n,则矩阵A的所有特征值位于下列区域之中:




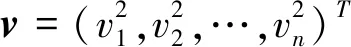
设G=diag(u1v1,u2v2,…,unvn),由引理4知,则有:
由引理5知,有
|ρ(A∘B)-aiibii||ρ(A∘B)-ajjbjj|≤Ri[G-1(A∘B)G]Rj[G-1(A∘B)G]
2.设A∘B为可约矩阵,则A和B中至少有一个是可约的。设P=(pij)是n阶置换矩阵,p12=p23=…=pn-1,n=pn,1=1,其余pij的都为零。对任意的ε>0,让ε→0使得A+εP,B+εP是不可约非负矩阵,用A+εP,B+εP分别代替A和B,让ε→0,由连续性,可知结果成立。
定理2 设A=(aij)∈Rn×n是非负矩阵,B=(bij)是逆M-矩阵,B-1=(βij),则有:
证明 1.设A∘B为不可约矩阵,则A,B,JA都不可约,由于B是逆M-矩阵,则B≥0,存在正向量u=(u1,u2,…,un)T,v=(v1,v2,…,vn)T满足JAu=ρ(JA)u,BTv=ρ(BT)v.
即有:

设V=diag(v1,v2,…,vn),则C=VB-1=(βijvi)是严格按列对角占优矩阵,由引理3得,


设F=diag(f1,f2,…,fn),则有:
由引理5知,有:
|ρ(A∘B)-aiibii||ρ(A∘B)-ajjbjj|≤Ri[F(A∘B)F-1]Rj[F(A∘B)F-1]
即:
2.设A∘B为可约矩阵,则A和B中至少有一个是可约的,由引理4知,B-1的顺序主子式都是正的。设P=(pij)是n阶置换矩阵,p12=p23=…=pn-1,n=pn,1=1,其余的pij都为零。 对任意的
ε>0,让ε→0使得(B-1-εP)-1的顺序主子式都是正的,则A+εP,(B-1-εP)-1分别是不可约非负矩阵和不可约逆M-矩阵,用A+εP,(B-1-εP)-1分别代替A和B,让ε→0,由连续性,可知结果成立。
3 数值算例

由公式(1)得:ρ(A∘B)≤12.6429.由公式(2)得:ρ(A∘B)≤6.4286.
由公式(3)得:ρ(A∘B)≤5.8174.
利用本文定理1,得ρ(A∘B)≤5.3511.
实际上,ρ(A∘B)=4.2143.

由公式(4)得:ρ(A∘B)≤4.3285.由公式(5)得:ρ(A∘B)≤4.1524.
利用本文定理2,得ρ(A∘B)≤4.0842.
实际上,ρ(A∘B)=3.8178.
由例1和例2可知, 本文定理1和定理2的结果在一定程度上比文献[1~5]所得到的界值更精确,且更易于计算。

