不规则井眼固井环空流动压降变化规律

郑双进，刘涛，廖坤，李足平，杜冬楠，刘裕，潘祎

1.长江大学石油工程学院，湖北 武汉 430100 2.中石化胜利石油工程有限公司固井技术服务中心，山东 东营 257100

固井环空压力剖面的精确计算与控制非常重要，尤其是针对密度窗口较窄的地层，压力控制不好容易发生井漏或溢流等事故，影响施工安全和固井质量。由于地层纵向非均质性的影响，或存在严重盐膏层、泥岩段，井眼垮塌严重，井径扩大率不均匀形成“大肚子”不规则井眼十分常见[1]。据统计，全球泥页岩地层占75%，90%的井眼稳定性问题发生在泥页岩，有的层段扩径，有的层段缩径，很容易形成“大肚子”或“糖葫芦”不规则井眼[2]。从公开文献报道也可同样得知，国内各大油田也普遍存在不规则井眼油气井[3]。不规则井眼固井过程中易发生油、气、水窜问题，影响界面胶结质量，进而影响固井质量[4-8]。据调研，早在1986年FRANK等[9]就针对突扩流进行研究，得到了级联展开的纳维叶-斯托克斯解；王常斌等[10]建立了突扩管在低雷诺数条件下的物理模型，采用正交网格划分，对牛顿流体层流下的管路突扩情况进行了数值模拟，分析了管路突扩回流时速度和压力的流场的分布情况；朱晓星等[11]基于非均匀网格Lattice-Boltzmann方法对二维突扩流进行了数值模拟，并验证了该方法的适用性；刘晓利等[12]运用有限分析法求解Navier-Stokes方程，获得了二维突扩管流的数值解；夏庆福等[13]应用标准k-ε双方程模型对洞塞消能进行了数值模拟计算，与经验公式计算结果相比误差小于5%。前述研究均是针对突扩流进行的，而实际不规则井眼大多为井壁曲线呈弧线状的弧形凹面井眼，与突扩管形态存在一定差异，目前鲜有描述弧形凹面区域流场规律的理论模型相关报道，该区域的流动压降情况也无从得知。因此，建立一套能够描述弧形凹面区域流动压降的计算方法，分析弧形凹面区域的流动压降变化规律及影响因素，对于精细计算不规则井眼环空压力剖面十分重要。

1 不规则井眼流动压降分析

如图1所示，当固井流体从小直径环空进入大直径环空时，小直径环空中的流线可近似看作平行直线，井径变化区域会产生旋涡；当固井流体从大直径环空进入小直径环空时，流线收缩，井径变化区域也会产生旋涡[14]。以上2个过程的流动求解复杂，这里为简化求解，将流动区域划分为环形流动区域与弧形凹面流动区域。 相应地，整个流动区域内的压降为环形流动压降与弧形凹面流动压降之和。对于环形流动区域，使用Burkhart给出的幂律流体环空压降计算公式求解固井流体在该区域的流动压降[15]。对于弧形凹面流动区域，运用平板驱动流理论描述其流动问题，以下通过推导弧形凹面区域的能量方程来分析该区域的附加压降。

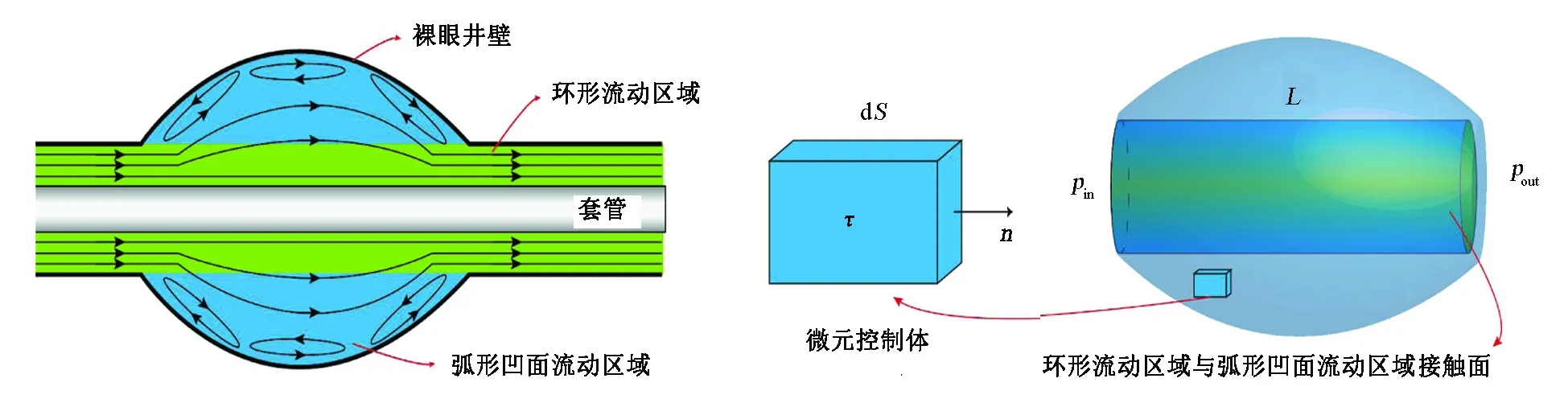
图1 弧形凹面井眼固井流体流动示意图 图2 微元控制体示意图 Fig.1 Schematic diagram of cementing fluid flow in the Fig.2 Schematic diagram of the element control body borehole with curved concave surface

如图2所示，弧形凹面流动区域任一微元控制体内能量守恒定律为体积τ内流体动能和内能的变化率等于单位时间内质量力和面积力所做功加上单位时间内给予体积τ的热量，则弧形凹面流动区域内的能量守恒定律可表达为：

(1)

式中:τ为微元体体积；S为微元体表面积；T为温度的微分；ρ为流体密度；Q为微元体内能；t为时间；v为速度矢量；n为微元面外法线方向单位矢量；F为体积力矢量；k为导热系数；q为热量；P为二阶张量，包含正应力与切应力。

全微分形式的能量变化率可转化为如下偏微分形式：

(2)

式中:vn为垂直于微元表面的速度。

根据奥高公式将面积分转化为体积分：

(3)

(4)

此时积分形式的能量守恒方程可转化为：

(5)

由于微元τ是任意的，且假定被积函数连续，由此可导出：

(6)

假定在流动过程中没有热量交换，即:

则有：

(7)

两边同时对时间t积分可得：

(8)

在t=0时刻，v=0，则有：

(9)

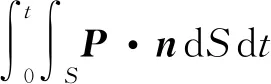
除了平板驱动切应力及正应力外，其余的正应力与切应力均为内力，整个弧形凹面流动区域内力所做功总和为0。另外，考虑到壁面无滑移边界条件，说明壁面并不对流体做功，故只有重力及驱动剪切力对流体做功，所做功即为整个弧形凹面流动区域的动能。

在图2中的环形流动区域与弧形凹面流动区域接触面处功能关系为：

(10)

式中：S0为环形流动区域截面积。

当|v|dt=L时，弧形凹面区域的附加压耗：

(11)

2 弧形凹面区域流动控制方程

2.1 连续性方程

在固井流体中取由一定流体质点组成的物质体，根据质量守恒定律，并假定固井流体是不可压缩流体，广义坐标系下的连续性方程可表示为：

(12)

考虑径向对称性，则柱坐标系下的连续性方程为：

(13)

式中:vr为径向速度；vz为轴向速度。

2.2 动量守恒方程

广义坐标系下的动量守恒方程可表示为：

(14)

考虑径向的对称性后，动量守恒方程在柱坐标系下表示为：

(15)

2.3 柱坐标下控制方程的无量纲化

取流场的特征长度、特征速度、特征时间、特征压力，将控制方程无量纲化：

(16)

无量纲化后的方程统一为：

(17)

式中：Re为雷诺数；X、Y分别为x与y方向特征化后长度；U、V分别为x与y方向特征化后速度；p为特征化后压力。

将控制方程无量纲化以后，可以避免控制方程中物理参数在量级上的悬殊差异，从而减少不必要的数值误差和精度损失，同时可减少控制方程中的常数运算而将常数转化成几个相似参数；此外，还易于实现数值计算中的相似模拟，从而使计算结果更具通用性。

3 弧形凹面区域流场求解

3.1 控制方程的离散

对于驱动流问题，目前最常用的解法是交错网格法。所谓交错网格就是把速度U、V及压力p(包括其他所有标量场及物性参数)分别存储于3套不同网格上的网格系统中。其中速度U存在于压力控制容积的东、西界面上，速度V存在于压力控制容积的南、北界面上，U与V各自的控制容积是以速度所在位置为中心，求解过程中所建立的交错网格如图3所示。偏微分控制方程组采用有限差分进行离散，对速度项采用显式格式，对压力梯度项采用隐式格式，空间所有导数项均采用中心差分格式，时间步长为Δt，空间步长为ΔX与ΔY。

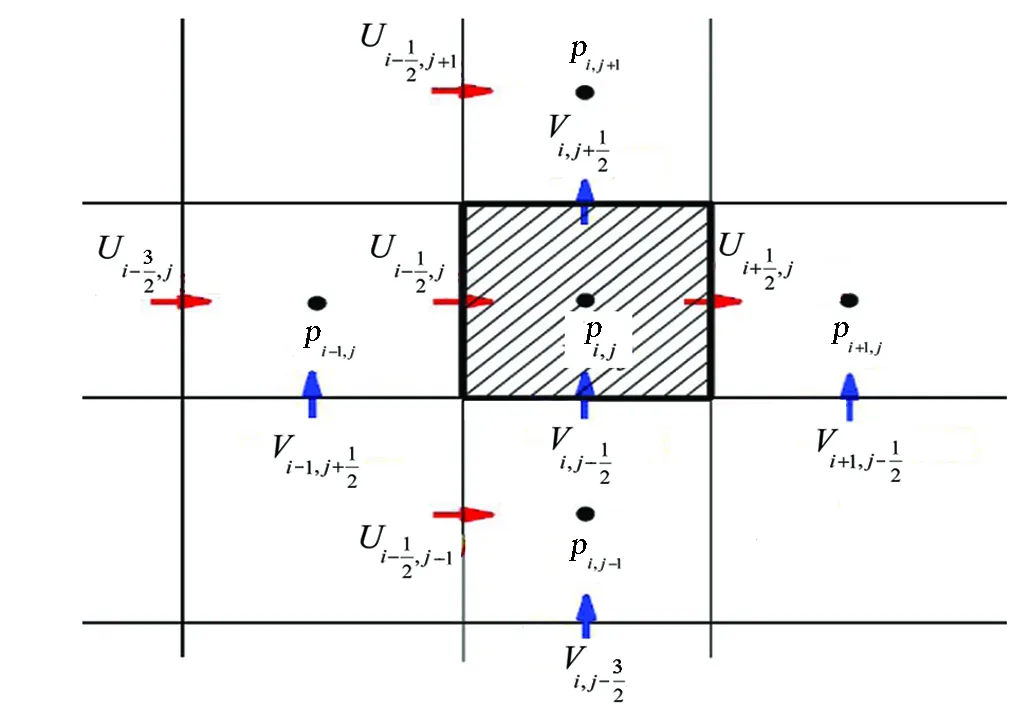
图3 交错网格示意图 Fig.3 Schematic diagram of staggered grid

将离散后的动量方程代入离散后的连续性方程中得：

(18)

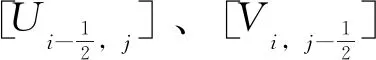
3.2 求解流程

1)定义变量，赋初始值、边界值与参数值，如Re；

2)确定网格信息，如空间步长、时间步长：ΔX，ΔY，Δτ；

4)将离散动量方程代入离散连续方程构造统一的压力方程；

5)以中间速度为源项求解压力方程，采用迭代法直至收敛；

7)令t=t+Δt，返回步骤3)，以最新值进行下一步推进，直至推进到稳态为止；

8)有且需求稳态值时一直推进到稳态为止，无或不求稳态值时推进到一定时刻终止。

4 实例应用

4.1 实例计算

基于上述建立的理论模型和求解方法，运用VB6.0程序设计语言开发了弧形凹面井眼流动计算分析软件，可计算弧形凹面井眼段的流体流动压降变化规律，并分析井径扩大率和流体排量对流动压降的影响规律。

南海某井固井前实测井径曲线如图4所示，合理简化设置模型总长1m，弧形凹面井眼段长0.5m，上下两端的规则井眼段各长0.25m，钻头直径444.5mm，套管外径339.7mm；弧形凹面井眼剖面线为正弦曲线，流经弧形凹面井眼段的固井流体密度为1.8g/cm3，流性指数n为0.82，稠度系数k为0.53Pa·sn，黏度为40mPa·s。为了对比分析不同井径扩大率和不同排量条件下的流动压降，井径扩大率依次为0、20%、30%、40%、50%、60%，流体排量依次取30、40、50L/s，计算结果如图5所示。

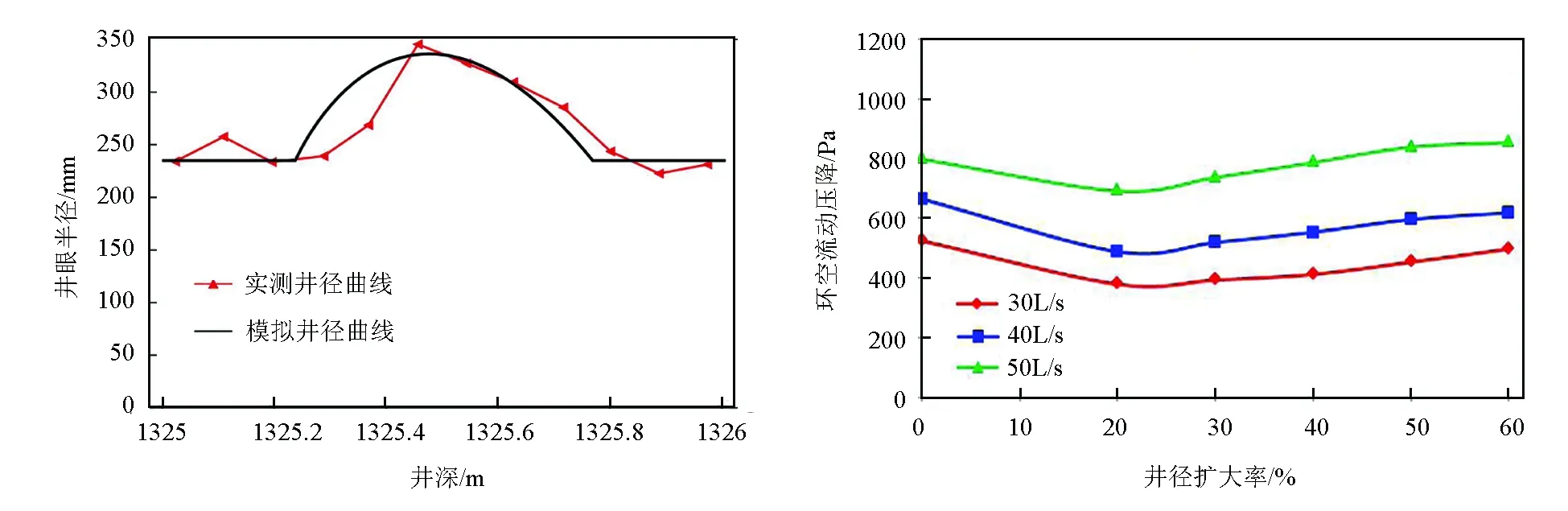
图4 南海某井固井前实测井径曲线 图5 不同流体排量下的流动压降计算结果 Fig.4 Measured diameter curve of a well in the South Fig.5 Calculation results of flow pressure drop at China Sea before cementing different fluid displacements

4.2 数值模拟

采用Fluent软件进行数值模拟验证。由于井下弧形凹面井眼段的入口压力及出口压力未知，故在进行数值模拟时采取入口流量条件，出口压力条件(压力为0)。其网格划分情况(以井径扩大率50%为例)如图6所示，排量分别为30L/s与50L/s时模拟结果如图7所示。

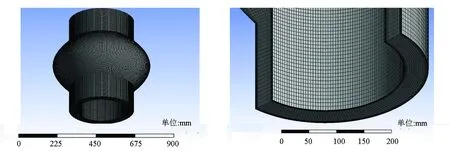
图6 弧形凹面井眼段流动数值模拟网格划分图Fig.6 Numerical simulation results of flow pressure drop under different fluid displacements

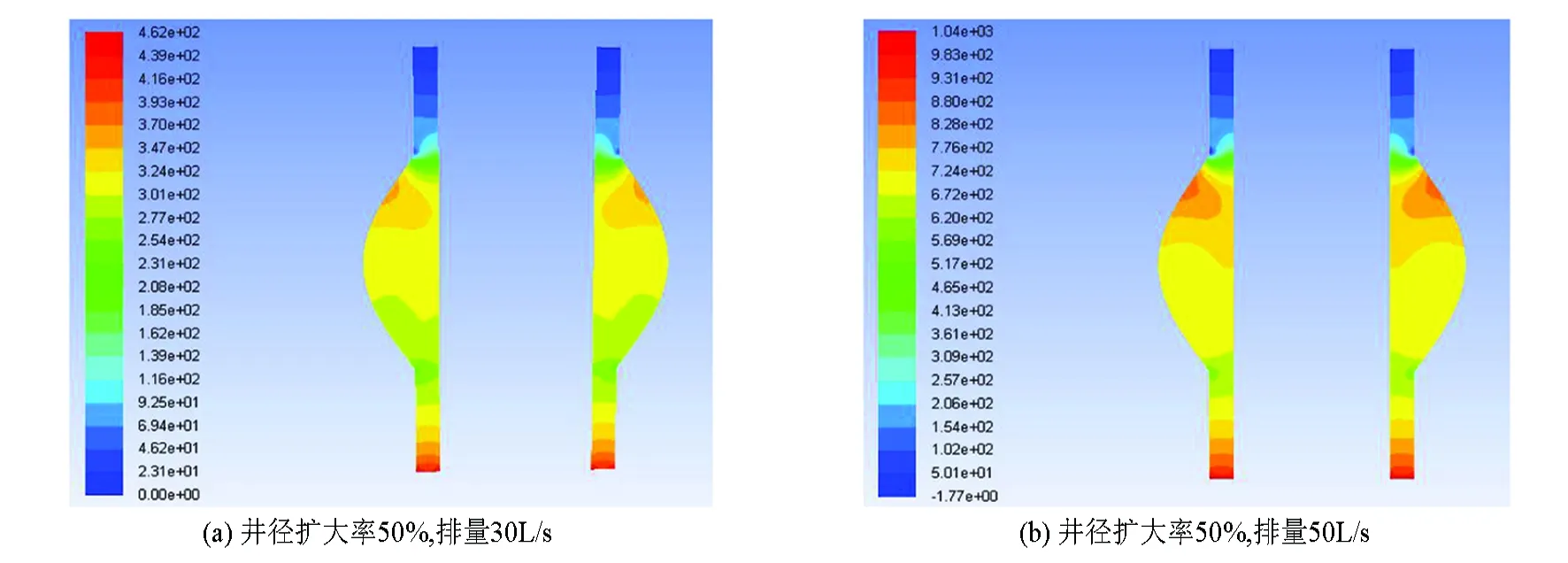
图7 弧形凹面井眼段压力场图Fig.7 Pressure field diagram of the borehole with curved concave surface

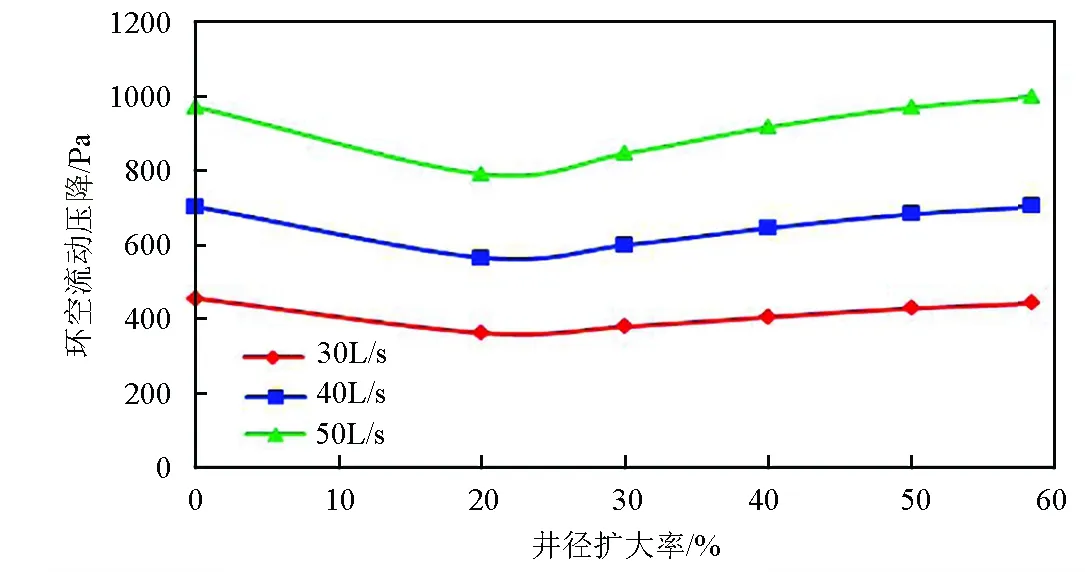
图8 不同流体排量下的流动压降数值模拟计算结果 Fig.8 Numerical simulation results of flow pressure drop under different fluid displacements

依据数值模拟结果，绘制弧形凹面井眼流动压降随井径扩大率变化数值模拟曲线，如图8所示。

从图5和图8可以看出，在同等井径扩大率条件下，排量越大流动压降越大；在同等排量条件下，随着井径扩大率的增大，流动压降呈先减小后增大的趋势；在常见的井眼扩径范围内，弧形凹面井眼的流动压降小于正常井眼的流动压降。对比图5和图8，软件计算和数值模拟分析结果大体一致，且趋势相同，数据偏差分析如表1所示。

从表1可以看出，软件计算结果和数值模拟分析结果偏差均在15%以内。由于环空压降在井筒压力中所占的比重较小，因此该数据偏差在工程计算允许的误差范围内，由此可认为笔者所建立的模型能够描述弧形凹面区域的流动问题，对于固井环空压力的精细计算具有一定的参考价值和指导意义。

表1 软件计算结果与数据模拟计算结果偏差分析

5 结论

1)通过建立弧形凹面井眼条件下的流动压降方程,分析了压降的构成，建立了环空流体控制方程，研究确定了求解方法与流程，并开发软件进行了计算分析，运用Fluent数值模拟软件进行了验证，软件计算结果与数值模拟结果偏差在工程允许的误差范围内，为固井环空压力的准确计算与控制提供了参考。

2)软件计算与数值模拟结果表明在同等井径扩大率条件下，流动排量越大，弧形凹面井眼段的流动压降越大；在常见的井眼扩径范围内，弧形凹面井眼的流动压降小于正常井眼的流动压降。