基于最小二乘椭圆拟合的井径测量面偏角修正方法
□ 刘春光 □ 刘树林 □ 袁 率
上海大学 机电工程与自动化学院 上海 200072
在石油钻井作业过程中,井径测试是必不可少的一项工作。在传统的井径测算过程中,往往将井径仪的测量平面与实际井眼的径向截面看作同一平面[1](如图1所示)。然而在测井过程中,由于井径仪的位置与姿态始终发生着变化,所以其测量面与实际井眼的径向截面往往是不重合的(如图2所示),尤其是在水平井造斜段,两者之间的偏角更为明显。面偏角的存在,不仅使井径计算变得困难,而且给井下工具的安装、使用等带来不便[2,3]。因此,有必要研究井径测量中面偏角的修正方法,以及此状态下井径的拟合算法。
传统井径计算常采用最小二乘曲线拟合方法[4~6],通过整合每个测量点的测量值,将井眼拟合成一个圆或椭圆,从而直接得出井径值。这种方法忽略了面偏角对井径计算的影响,因此在大斜度井段,其井径计算值与实际值存在着较大偏差。
针对上述情况,笔者提出了一种基于最小二乘椭圆拟合的井径测量面偏角修正方法:将实际井眼的径向截面近似看作一个圆形,通过最小二乘拟合的方法将井径测量面拟合为一个椭圆。由于实际井眼的径向截面与井径测量面的交线为椭圆的短轴,所以能够计算出两面之间的偏角,并实现对井径值的校正。本文以六通道式超声波井径仪为例,阐述了该方法在井径测算中的应用过程。
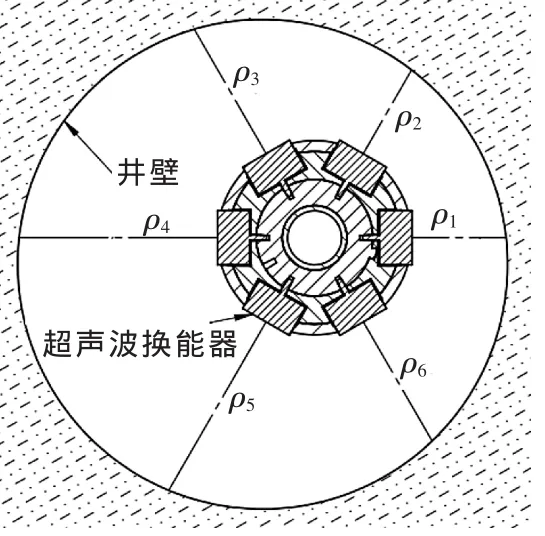
▲图1 井径测量示意图
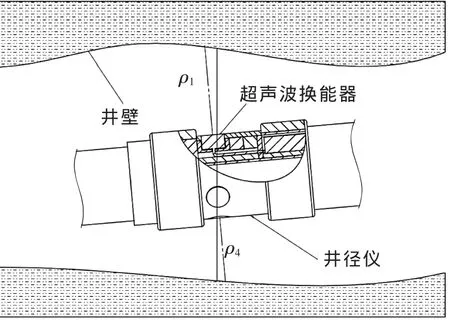
▲图2 井径测量面偏角示意图
1 径向截面圆的拟合算法
对于六通道式超声波井径仪,其工作过程中每个时间点可产生6组距离数据,分别对应6个超声波传感器。考虑到6个测量传感器沿圆周均匀排列,因此使用极坐标的形式进行计算更为方便。
当井径仪测量面与井眼径向截面不重合时,可采用最小二乘法将井眼径向截面拟合为一个圆形[7,8](如图3所示),其极坐标换算:

设拟合圆心直角坐标 O1(x0,y0),极坐标(ρ0,θ0),拟合圆半径为 R,样本点 Bi(ρi,θi)(i=1,...,6),且 θi=(i-1)。
圆的方程:

▲图3 拟合井眼径向截面为圆

极坐标形式:

由最小二乘法,计算样本点 Bi(ρi,θi)到拟合圆心O1(ρ0,θ0)的距离与拟合圆半径 R 的平方差:
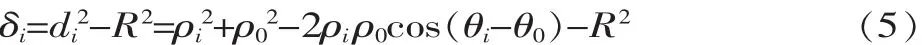
设目标函数为:
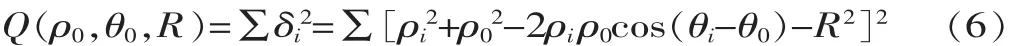
则要求:
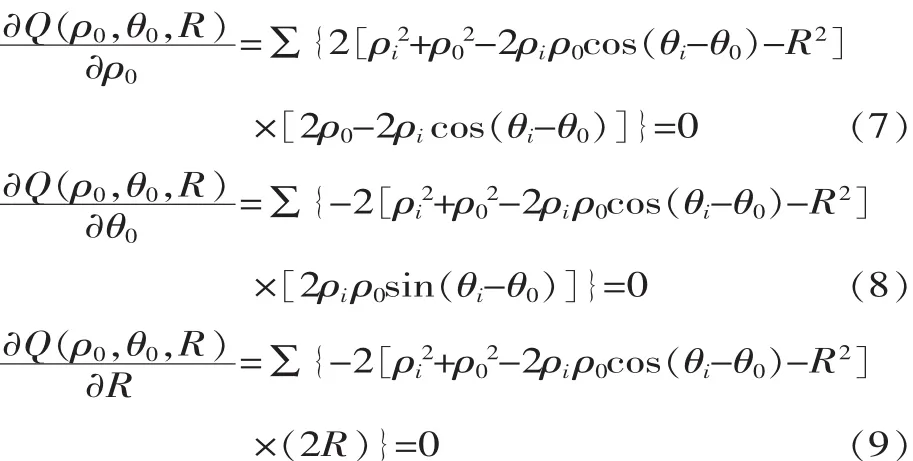
令:
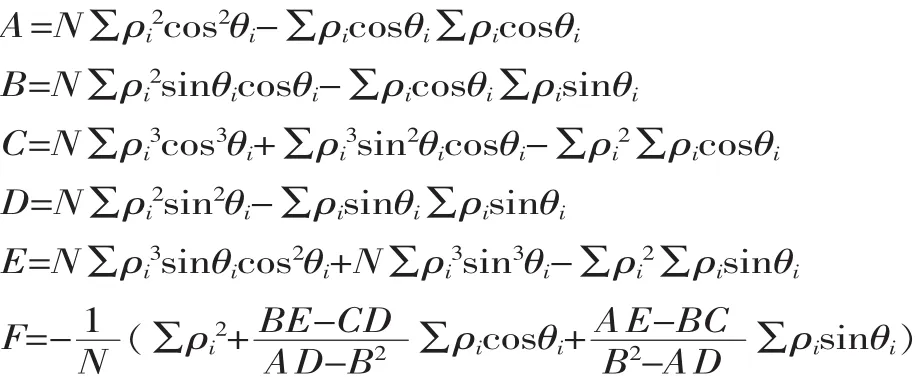
解得拟合值:

2 面偏角状态下的井径拟合算法
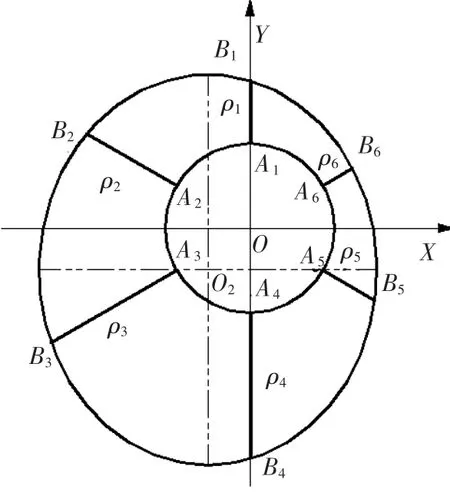
▲图4 拟合井径仪测量面为椭圆
当井径仪测量面与井眼径向截面间存在偏角时,可采用最小二乘法将井径仪测量面拟合为一个椭圆[9,10](如图 4 所示)。
已知常数项归一后的平面任意位置椭圆一般方程为:
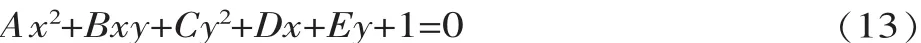
根据样本点 Bi(ρi,θi)(i=1,...,6),可得函数:
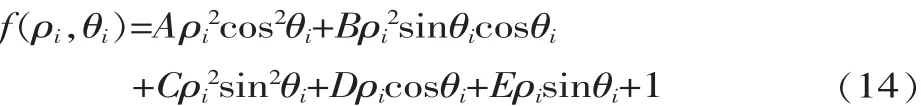
由最小二乘法原理,构建目标函数:
F(A,B,C,D,E)=Σ(Aρi2cos2θi
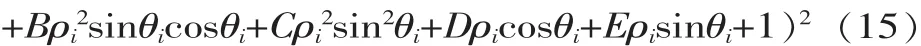
解线性方程组,得椭圆方程的系数A、B、C、D、E。
设拟合椭圆的几何中心为 O2(ρ0,θ0),则解得:

椭圆的长轴倾角:

椭圆的长半轴:
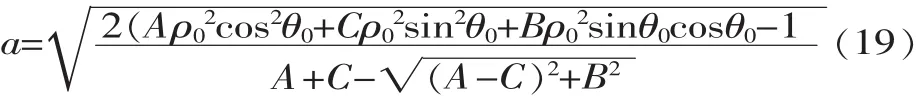
椭圆的短半轴:

以基准面1代表井径仪测量面,基准面2代表井眼径向截面,则两面之间的几何关系如图5所示。由于椭圆短半轴长度等于圆的半径长度,所以井径D=2b;由几何关系可知面偏角:
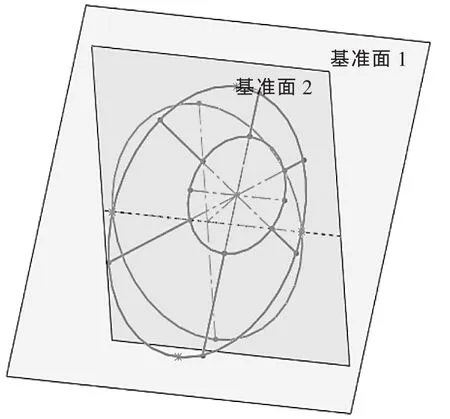
▲图5 面偏角几何示意图

▲图6 井径测量仿真图形

表1 井径测量仿真结果
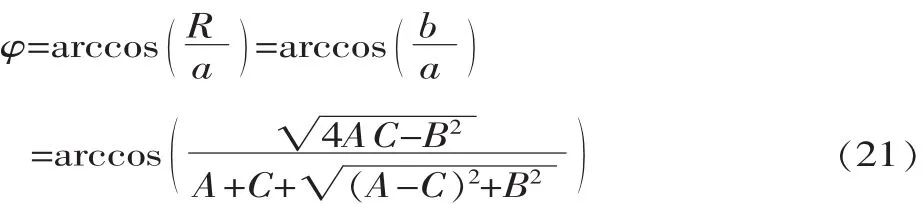
3 MATLAB仿真结果分析
借助MATLAB软件,可以对井径测试过程进行仿真,并检验上述修正算法的有效性。井下测量的仿真图形如图6所示,可分为以下两个部分。
(1)给定三维井壁信息:以空间三维曲线(用点划线表示)为井径中心线;外层的弯曲线框模拟井壁,其内径沿空间三维曲线的伸展方向发生变化。
(2)模拟井径测量状态:以虚线段模拟当前井径仪的姿态;椭圆形阴影面垂直于虚线段,为当前井径仪的测量平面;井径仪上6个传感器的长度测量值由6条短线表示。
在得知6个长度测量值(即6条短线的长度)后,应用上文所述偏角修正方法,由MATLAB计算出当前位置的井径大小与偏角值。
通过改变初始条件,得到了5组仿真结果见表1。结果表明,采用井径测量偏角修正方法后,得到的井径值与井径中心位置比直接使用圆拟合的方法所得到的数值更为准确。而且,在计算过程中得出了井径测量时的偏角信息,这也是传统方法所不具备的。
4 结论
分析了面偏角的产生原因及其影响;结合井径仪的特点,提出了基于极坐标的圆与椭圆拟合算法;根据面偏角的几何关系,提出了面偏角的计算方法以及井径测量值的修正方法。最后,通过MATLAB仿真结果,证明了该种修正方法可以提供任意位置处面偏角的较为精确的拟合值,并能有效提高井径测算的准确度。
[1] 周灿灿,王昌学.水平井测井解释技术综述[J].地球物理学进展,2006(1):152-160.
[2] 刘文喜,张鹏,韩侠.井下工具可靠性设计[J].石油矿场机械,2009(7):56-59.
[3] 刘吉成,刘锐,唐友福,等.水平裸眼井径仪测量臂线性化及井径数据同步[J].机械制造,2012(1):15-18.
[4] 余厚全,涂继辉,李国军,等.超声成像测井井径的椭圆拟合及偏心时间图像的校正[J].测井技术,2011(5):418-421.
[5] 赵兵帅,黄腾,欧乐.基于椭圆拟合的隧道断面监测及其应用[J].水利与建筑工程学报,2013(2):130-133.
[6] 张健.超声成像测井中井径图像的偏心修正方法[J].应用科技,2013(5):62-65.
[7] Gander W,Golub G H,Strebel R.Least-squares Fitting of Circles and Ellipses[J].BIT Numerical Mathematics,1994,34(4):558-578.
[8] 闫蓓,王斌,李媛.基于最小二乘法的椭圆拟合改进算法[J].北京航空航天大学学报,2008(3):295-298.
[9] 马向南,李航,刘丽丽,等.最小二乘改进算法及其在椭圆拟合中的应用[J].河南科技大学学报(自然科学版),2014(3):18-22.
[10] Andrew Fitsgibbon,Narizio Pilu,Robert B Fisher.Direct Least Square Fitting of Ellipse [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1999,21(5):476-480.

