“好问题”促生图示优化儿童数学认知结构的实践

顾娅娟

【摘要】“好问题”不同场域的构建丰富了小学数学问题的解决方法;以关联性图示优化数学认知结构是对儿童良好数学认知结构的探索;“好问题”促生图示优化儿童数学认知结构，这是发展学生核心素养理论的校本化开发与提炼.本文主要从五个方面进行实践研究.

【关键词】好问题;图示;优化;数学认知结构

【基金项目】本文系江苏省教育科学“十三五”规划2020年度青年专项普教重点资助课题《“好问题”促生图示优化儿童数学认知结构的案例研究》部分研究成果（立项批准编号：C-a/2020/02/19）

“好问题”的解决是关联图示生成的良好场域，儿童数学认知结构的形成、优化则是关联图示的机制与结晶.传统研究以思维导图、知识结构图为主，以知识点或单元名为核心，而“好问题”促生图示优化儿童数学认知结构是运用图示让儿童给未知的数学世界画图，每个图示是以问题解决为平台，以数学思想方法及个体素养为核心的动态发展结构.具体表现为：这是儿童由问题解决到问题解决，再到问题解决的过程;是儿童关联、融通，再关联、融通的过程;是儿童一幅幅图示生发、生长、发展的过程.

一、学会“好问题”图示描述，唤醒学生的审视力

《义务教育数学课程标准（2011年版）》指出：“利用图示描述和分析题目，可以帮助学生直观地理解数学，在整个数学学习的过程中都发挥着重要作用.”小学生由于逻辑思维能力发展的局限性，对于一些复杂的数学题目很难理解，直接用算术的形式无法解决，但是，如果能够合理应用“图示”来描述题目意思，很简明、直观地呈现出来，学生就能清晰地看到题目中隐含的数学本质，理解题目本意，从而更好地解决问题.

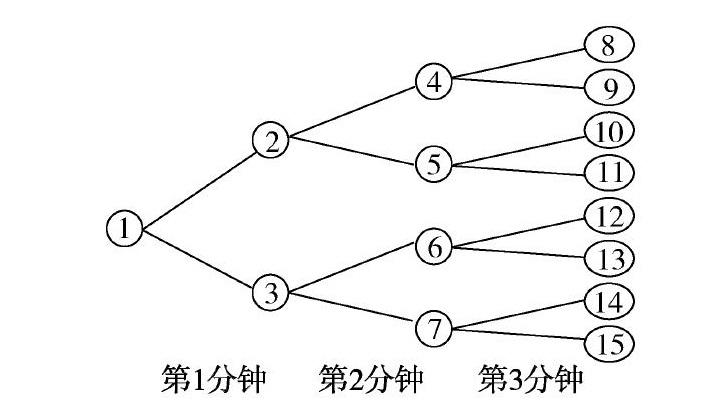
例如，在教学中有这样一道练习题：现在有一件紧急的事情要通知给全校的学生，用打电话的方式，第一个人通知到2人，再由这2人分别通知到2人，以此类推，每人每分钟可以通知2人，3分钟可以通知到多少人？这是一道较复杂的题，不用“图示”进行描述很难理清数学思路.因此，教师引导学生画出图示（如下图）.

从图示中学生很直观地看出第一分鐘通知了2人，第2分钟通知了4人，第3分钟通知了8人，一共通知了2+4+8=14（人）.接着教师继续提问：请你猜一猜5分钟能通知到多少人.学生可以继续画图示答题，通过观察图示可以很直观地发现规律.5分钟能通知到2+4+8+16+32=62（人）.

我们从上述教学中发现：“好问题”如果不被理解就没有任何意义，而通过图示的解释，给了学生视觉冲击，使学生能很容易地在图示中看出每个量之间的关系，从而使数学题目简单化，帮助学生准确理解题意.

二、学会“好问题”图示分类，凸显学生的思维力

对于如何提出“好问题”，教师要引导学生学会“好问题”图示分类.“哪些问题其实问的是同一件事？” “哪些问题其实可以归为一类？”“哪些问题不用思考就可以找到答案？而哪些问题需要通过深入地探索才能给出结论？”学会分类，让学生不再提出重复的问题，使学生透过问题的表层含义，触摸问题的内在实质.有些问题指向信息的获取，有些问题指向深入的探究.

例如，在教学“倍”的知识时，教材主要分为两类题型：一类是“求一个数的几倍是多少”，另一类是“求一个数是另一个数的几倍”.其中“求一个数的几倍是多少”应该列乘法算式计算，“求一个数是另一个数的几倍”应该列除法算式计算.在教学过程中，我们发现：小学生对这两种题型总是弄不清楚，练习的错误率很高.对此，教师在设计教学时，特别关注这两种题型的理解，让学生用自己喜欢的方式画一画.出示题目：（1）圆有6个，三角形的个数是圆的3倍，三角形有多少个？（2）圆有6个，三角形有3个，圆的个数是三角形的几倍？让学生先在作业纸上独立完成列式计算，并在下面的方框里画图解释算式的意义，然后和同桌讨论后各自再编一道对应的题目.直接看文字题目，学生会觉得这是同一道题，然后就都用乘法或者除法来计算了，教师很智慧地借助图示来帮助学生区别两类题型的不同，这样操作很直观、很明显.我们从上述教学中发现：通过图示，我们还可以有效地对“好问题”进行分类，这样的方式会比学生直接去读文字的题目要更直观，更好理解.很多时候小学生很容易将学过的知识弄混，学会“好问题”图示分类有利于学生清晰地建构认知结构，凸显学生的思维能力.

三、学会“好问题”图示对比，提升学生的判断力

著名教育家乌申斯基认为，“比较是一切理解和思维的基础……”对比法是小学数学教学中常用的学习方法之一.“好问题”图示对比就是利用图示进行对比，使得对比更直观，问题解决更有效.教师要充分发挥这一方法的作用和效果，在使用时必须注意学生爱比较的性格特征.但是，爱比较不等于会比较.这就有待教师引导学生学会“好问题”图示对比，以便提升学生的批判力.

例如，在进行“角的初步认识”中有关“角的大小”的教学活动时，为了让学生充分感受角的大小和什么有关，教师设计了如下探究活动：1.做一做，让学生用小棒做出一个角放在数学书的封面上;2.指一指，向同桌介绍角的各部分名称;3.说一说谁做的角大，谁做的角小，为什么;4.想一想怎么比较角的大小，角的大小和什么有关.再请两名同学到黑板上用磁性小棒分别摆出一个角，然后说一说他们是怎样进行比较的.教师在巡视的过程中发现有几组学生做的两个角的大小相差很大，故能用肉眼看出谁大谁小;有几组同学做的角的大小相差无几，很难判断，这几组同学也是用肉眼直接判断觉得一样大，这样是不严谨的;有几组同学在用量角器比画，但这是我们目前还没有学到的知识.在学生产生了“好问题”之后，教师准备了两个用纸板做好的三角形，并且这两个三角形的颜色不同，其中一个三角形是红色的，另一个三角形是黄色的.教师先让学生在两个三角形中分别找出一个角，做上记号，利用重叠法进行比较，把较大的角放在下方，较小的角放在大的角的上方，很直观就能比较出两个角的大小.教师再将学生的目光拉回到刚刚的磁性小棒摆的角上来，让学生想一想可以怎样进行比较.学生立刻发现，也可以将两个角进行重叠，看角两边的小棒张开的角的大小，张开大的角一定比张开小的角要大，最后总结得到：角的大小和角两边张开的大小有关.

在上述教学中，教师先让学生自主探究，动手做角，然后判断角的大小，从中发现“好问题”：当两个角的大小很接近时无法直接用肉眼比较出大小，怎么办？引发学生思考.通过图示对比优化学生的认知结构，从而提升学生的判断力.

四、学会“好问题”图示融通，激发学生的想象力

爱因斯坦说过，“想象力比知识更重要……”数学是一门相对比较抽象的学科，对学生的想象力的需求较大.在小学数学教学中，教师要怎样激发学生的想象力呢？首先要有一个“好问题”做平台，运用图示想象法，将新问题与旧知识进行融通，使得相对抽象的数学知识变得有形，在培养学生想象力的同时，解决新旧知识的融通问题，优化学生的已有认知结构.

例如，在教学“乘法的初步认识”中有关“乘法的意义”的内容时，有这样一道练习题：你能出一道用3×4解决的问题吗？对于这道题，教师要先引导学生回忆在之前的学习过程中，什么情况下是用3×4这个算式解决的，让学生画出图形，说一说.比如，学生想到了3个4相加可以用3×4解决;4个3相加也可以用3×4解决.教师要继续追问：3个4和4个3分别可以用什么样的图形表达呢？这样一问，学生的思路就被打开了，他们有的画出4个圆一堆，画这样的3堆表示3个4，画3个三角形为一堆，画了这样的4堆来表示4个3;有的画了4个苹果为一堆，画这样的3堆表示3个4，画3个草莓为一堆，画了这样的4堆来表示4个3……用图示融通新旧知识，简洁明了.

在上述教学中，教师让学生通过图示法对新知识进行想象，将新旧知识进行联想和融通，并将抽象的数学问题转化成图示表达，体现了数学简洁美的同时，加深了学生对乘法意义的理解，从而激发了学生的想象力.

五、学会“好问题”图示联想，激活学生奇思妙想

在教学中，教师经常通过联想让学生联系相关的概念、公式，沟通知识之间的内在联系，为解决数学问题提供良好的基础.通过联想可以使原来零散的相关知识点建立有机联系，变成相对集中的知识块和知识链，从而优化学生的认知结构.在“好问题”的驱动下，教师可以通过图示联想，将相关知识点之间的内在联系用图示直观地展示出来，扩大学生的认知空间，助力学生从多方面、多角度展开数学思考，激活学生的奇思妙想.

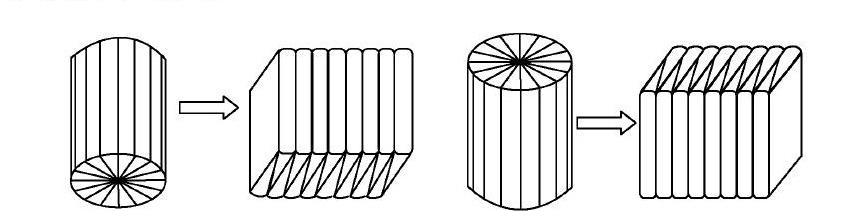
例如，在教学“圆柱的体积”时，有这样一道题：把一个高6分米的圆柱切拼成近似的长方体，表面积比原来增加了48平方分米.原来圆柱的体积是多少立方分米？教师先让学生思考：看到这道题，你能想到什么？你有什么想问的问题吗？生1：我想到了圆柱的体积公式.生2：我有个疑问：表面积哪里增加了？生3：圆柱怎么能切拼成长方体？生4：我想到了圆柱向长方体转化的那个图……于是，教师向学生展示下图：

从图示可以看出：增加的表面积就是长方体的左右2个侧面，其中侧面长方形的宽就是圆柱底面的半径，长方形的长就是圆柱的高.根据长方形的面积公式求出圆柱底面半徑等于4分米，再根据圆柱的体积公式求出原来圆柱的体积为301.44立方分米.

在上述教学中，如果没有图示联想，学生很难想象出怎样把圆柱进行切拼，很难理解切拼后表面积增加的是哪部分.通过图示联想，学生很清楚地知道：长方体的上下底面就是圆柱的上下底面，长方体的前后面就是圆柱的侧面，所以多出来的部分就是长方体的左右两个侧面.

结 语

总之，有好问题，思维才有方向;有好问题，思维才有动力;有好问题， 思维才有创新;有好问题，思维才有发展.“好问题”促生图示，让数的意义建构更准确;让运算的算理探索更有味儿;让数学规律的发现更有意义;让数量关系更清晰明了;让知识体系的架构更完整，有效地优化了儿童数学的认知结构.

【参考文献】

[1]丁浩波.“互联网+”在小学数学课堂教学中的应用探究[J].科技资讯，2020，18（26）：35-37.

[2]王旭彬.注重体验，优化课堂：浅谈小学数学教学策略[J].科学咨询，2020（23）：281.

[3]贺永应.基于核心素养的小学数学课堂教学的实践思考[J].才智，2020（15）：162.