基于二次相似性度量的即时学习转炉炼钢终点碳温软测量方法

曾鹏飞，刘 辉

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

0 引言

钢铁工业在国民经济生产中占有重要地位，标志着国家经济发展的程度。由于高生产率和低成本的优势，全球近65%的钢厂使用转炉炼钢BOF(basic oxygen furnace)[1]。冶炼终点钢水中的碳含量和温度决定了钢的质量，因此对转炉终点碳温进行控制尤为重要，而实际生产中受工人经验、熟练程度和主观情绪等影响，依靠人工经验预测终点碳温的方法因预测精度较低，导致炼钢生产效率低，资源浪费严重。

通常，氧气转炉终点碳温测量方法分为直接测量和间接测量两大类。直接测量的方法检测熔池内钢水碳温时大多采用副枪检测法[2]，即利用专门的探头和检测工具测量熔池内钢水的碳温，其测量精度高但不能连续实时测量，而且副枪探头长期处于高温腐蚀环境中，使用成本较高。在BOF过程中，加入的石灰石、铁水、废钢、吹氧量等过程生产数据与终点碳含量和温度存在非线性关系[3]，为间接测量碳含量和温度提供了理论依据，其中基于物料平衡和热平衡的终点碳温预测模型过分依赖炼钢原材料初始条件的稳定性和操作过程平稳性。当前国内钢厂铁矿石、废钢等原材料的品质波动很大，导致机理模型的建立十分困难。随着人工智能技术的发展,智能模型被广泛用于转炉炼钢过程建模。王心哲等[4]将经过变量选择后的特征作为转炉炼钢模型的输入进行终点预测；Cox等[5]采用BP(back propagation)神经网络模型对BOF终点碳温进行预测；柴天佑等[6]综合使用径向基函数(Radial Basis Function, RBF)神经网络对转炉终点的碳含量和温度进行预测；Zhou[7]和Tang[8]等人分别根据生产线上传感器测量的相关数据，结合多输出最小二乘支持向量回归理论，建立了非线性终点碳温以及硅含量的预测模型。然而，非线性建模方法主要基于离线数据进行全局建模，实际炼钢过程中，受检测仪表和变送器等装置故障以及人工操作失误的影响，所采集的生产过程数据经常出现异常，导致预测模型与实际工况不匹配，很难在线更新全局模型，无法有效预测当前炉次的终点碳温，难以把握出钢的最佳时刻[9]。

当全局建模策略无法有效满足转炉炼钢终点碳温预测的实际需要时，常采用即时学习[10-11](Just-in-Time Learning, JITL)策略。围绕JITL策略的核心(即相似度准则问题)，Chen等[12]认为相似度准则仅与样本的输入信息有关，没有考虑样本的输出信息，因此将输入和输出变量信息综合起来构建自适应加权距离作为相似度指标；Niu等[13]将模糊C-均值方法与常用的JITL结合，首先通过模糊C-均值重构历史数据集，然后在重构的数据集中再采用JITL方法选取当前的局部样本建立软测量模型。然而，这类方法没有考虑JITL每次重新建立局部模型时耗时较长的问题，在转炉炼钢终点碳、温预测实时性要求较高的背景下效果不佳。Ge等[14]将计算前后两个相邻测试样本之间的相似度改进为计算当前时刻样本与上一更新初始时刻样本之间的相似度，可以有效解决这一问题。牛大鹏等[15]在文献[14]的基础上引入时间序列，并通过投影算法预测未更新时刻的输出并达到了一定的效果。然而，数据样本采用的相似度准则均属于一阶相似度(First-Order Similarity, FOS)准则，仅在FOS准则的基础上采用模型更新的方法，虽然可以有效提高模型的实时性，但是会相应降低模型的精度，而且基于角度和距离度量指标无法适用于数据波动大且具有时间序列的BOF炉次样本。

综上所述，本文从相似性度量准则出发，提出一种二次相似性(Quadratic-Order Similarity, QOS)度量策略来建立局部最优模型。QOS度量策略不仅充分考虑了样本的总体特征，还考虑了样本间的时间序列特性，使选择出的样本类内方差更小、类间方差更大，选择到的相似样本更合理。采用具有反馈补偿机制的长短期记忆(Long Short-Term Memory, LSTM)循环神经网络建模时，训练样本具有很强的时间序列，更加有利于模型对前一炉次样本信息的利用，增强了模型的泛化能力。最后，通过转炉炼钢终点碳、温预测仿真实验结果表明，本文所提方法可以有效解决数据异常问题，同时提高模型的预测精度。

1 基于二次相似性度量的即时学习策略

1.1 即时学习相似性度量策略

JITL的思想是相似输入产生相似输出，目的是从历史样本库X中选择与待测样本xq相似度最高的一组训练样本来建立当前的最优局部模型，其核心是相似度准则的选取。传统的JITL度量准则描述为

(1)

式中：s为待测样本xq与训练样本X之间的相似度值；λ为0～1之间的权值系数；d为两个样本间的二范数，θ为两个样本之间的夹角，计算公式分别为：

d=‖xq-xi‖2,

(2)

(3)

FOS准则仅考虑两个样本点对点之间的相似性，没有考虑多样本之间的相似性，忽略了样本的总体特征，使选择到的相似样本不够合理，虽然可以有效提高模型的实时性，但是相应降低了模型精度。

1.2 二次相似性度量策略

1.2.1 灰色关联度分析准则

给定包含N个炉次样本历史库[16]。数据表示为

(4)

式中X={xi∈Rm,i=1,2,3，…，N}，m为样本维数。假定当前待测炉次样本xq，QOS度量策略的目的是从历史样本库X中选择与xq相似度最高的一组训练样本来建立当前最优局部模型训练集，文献[17-19]和基础实验证明，传统的基于FOS度量时的角度和距离准则不适应于BOF炼钢中具有时间序列特性且波动较大的炉次样本。虽然文献[17]中的二阶相似度准则考虑了样本的总体特征，但是相比已有方法使选择到的相似样本更合理且速度更快，其二阶度量策略无法有效度量更高阶下的样本，且无法挖掘时间信息，导致所选择的局部样本类内、类间区的分度达不到最佳。

因此，本文采用灰色关联度分析(Grey Relation Analysis, GRA)准则和QOS度量策略衡量样本间的相似度，其GRA度量准则描述为

(5)

式中Dxi,xq为待测炉次样本xq与历史库样本X之间的GRA值，其计算步骤如下：

步骤1通过式(6)计算待测样本xq与历史库样本X间每一维度的差值，构成一个差值矩阵，结果如式(7)所示。

Δxi,xq(k)=|Xq(k)-Xi(k)|;

(6)

Δxi,xq(k)=

(7)

步骤2由式(7)获取两级极差的最大值Δ(max)和最小值Δ(min)：

Δ(max)=max(maxΔxi,xq(k))；

Δ(min)=min(minΔxi,xq(k))。

(8)

步骤3求差值矩阵中参考数列和比较数列的灰色关联系数

(9)

步骤4获取xq与历史库样本X间每一维度的关联度值

(10)

得到灰色关联度的值，进而采用式(5)求样本xq的最终训练样本集。

1.2.2 二次相似性度量策略的定义

定义1设转炉炼钢历史库样本为X={xi∈Rm,i=1,2,3,…,N}，当前待测炉次样本为xq。定义GRA度量的FOS初始模型样本集合Sp×m={s1,s2,…,sm}为球集合。

球集合中样本点的质量为xq与历史库样本X的GRA值，其不仅考虑了样本间点对点的相似度，还兼顾了炉次样本间的时间序列特性。

定义2为更好地建立局部模型，在球集合Sp×m={s1,s2,…,sm}中计算两两样本之间的FOS值得到SP×p矩阵，定义质心样本索引向量I=[i1,i2,…,ip]，max(I)为质心样本索引编码。

质心样本的确定使二次度量具有可行性，将两样本间拥有大多数共同FOS相似的样本纳入训练库，使其待测样本的训练库样本最佳。

QOS度量策略通过FOS度量建立初始球集合模型，确定质心样本点二次度量，建立最终局部模型。

QOS度量策略的伪代码如下：

输入：历史样本X={xi∈Rm,i=1,2,3,…,N}，测试样本xq。

输出：最佳训练样本库Sd×M。

for i=1:N

得到训练样本两两之间的相似度矩阵SP×M。

End for

for j=1:p

for j=1:p

通过GRA算法计算SP×m两两样本之间的FOS值。

End for

End for

得到训练样本两两之间的相似度矩阵SP×p，得到对应的质心样本索引矩阵I=[i1,i2,…,ip]，输出max(I)即为质心样本，记为Imax。

for i=1:N

计算训练样本X与Imax之间的FOS，获取阈值在0.8以上的样本，构成最佳样本库Sd×M。

End for

相比于FOS策略，QOS度量策略充分考虑了样本的总体特征，使选择的相似样本更合理。算法原理如图1所示，样本2为待测样本，样本1、样本3～样本9为历史库的部分样本。采用FOS策略度量时，只度量出将样本1、样本3～样本7，而样本8和样本9与样本3～样本7的相似度很高却被漏捡。QOS度量策略确定质心样本5后进行二次度量，可以将漏检的样本8和样本9重新纳入训练集。因此，QOS度量策略不但使训练样本的整体分布更加合理，而且使历史库中的样本与待测样本的整体相似度达到最高，更有利于预测待测样本。

本文从二次度量策略角度出发采用灰色关联度准则，不但兼顾了距离和角度的信息，而且挖掘出了炉次样本的时间信息，质心样本使QOS策略能够有效减小样本间的类内差距，增大类间差距，有利于提高模型的预测精度，解决了文献[17]方法中二阶度量策略无法挖掘时间序列信息且不能更好区分样本类内类间方差的问题。

2 转炉炼钢的终点碳、温预测模型

2.1 反馈补偿机制的长短期记忆网络

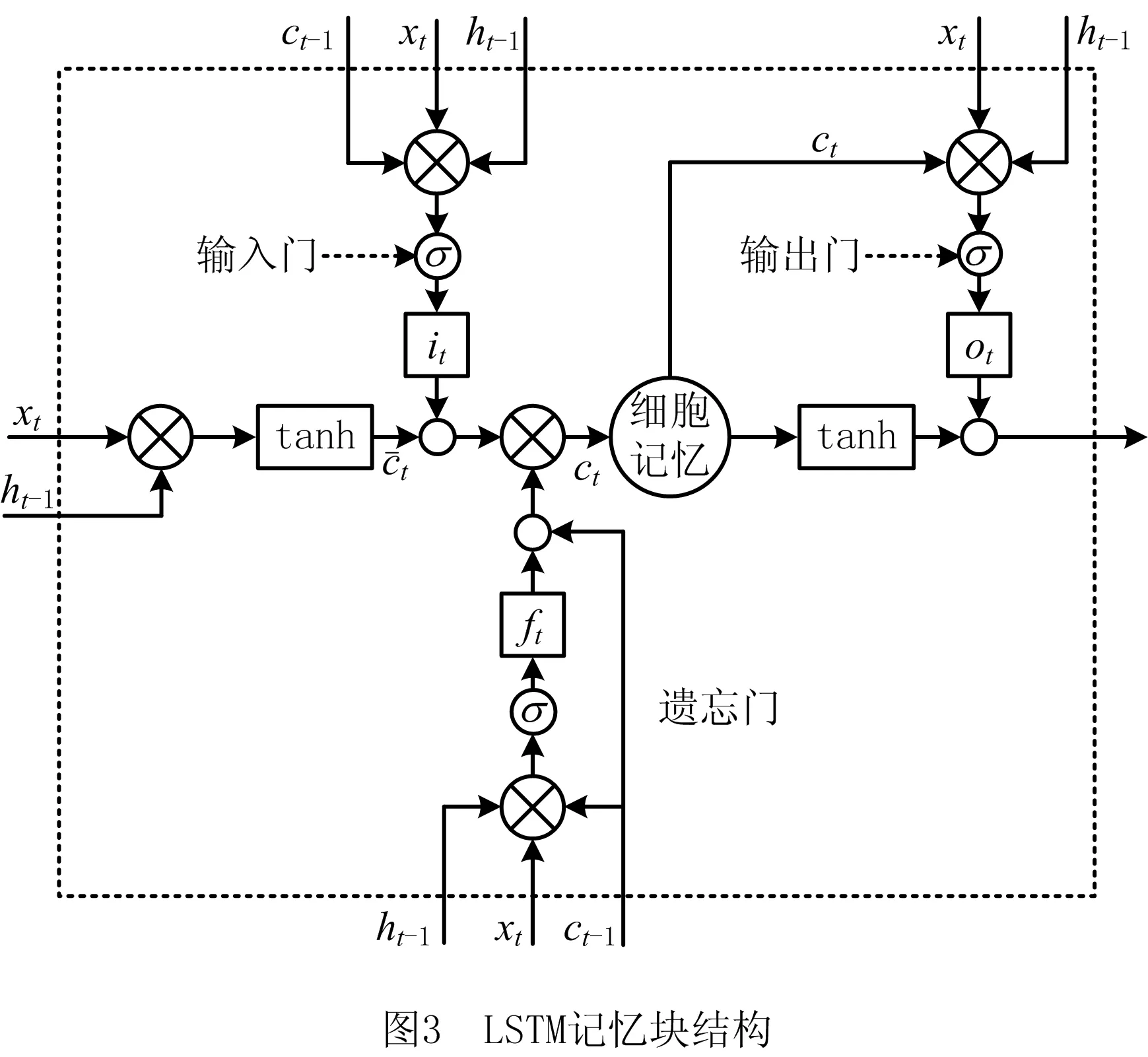
循环神经网络(Recurrent Neural Network, RNN)是一种深度神经网络，其最大的优势是将时序概念引入神经网络，从而使上一时刻输入的数据直接影响当前时刻数据，当RNN有足够的隐藏层数时，其能够以任意精度逼近需要预测的序列。然而，随着时间序列特征的增加，RNN会出现“梯度消失”问题，不利于准确预测终点碳温，因此LSTM在RNN的基础上增加了记忆模块、输入门、遗忘门、输出门。前期实验证明，将LSTM方法应用于具有时间序列的炉次样本数据来预报终点碳温具有较好的效果。由于炉次样本间生产工况的复杂性导致样本数据丢失或出错，本文在传统LSTM网络中将输出层反馈回输入层，改进后的网络不但可以提取层次间的特征，而且加入的反馈层融合了炉次样本间的序列特征，能够在数据残缺的情况下充分利用T-1炉次下的信息，使预测精度最优，并增强网络的抗干扰能力。实验证明，在数据有残缺或不合理的情况下，碳温预测精度仍在误差允许范围内。图2所示为改进的LSTM网络结构，图3所示为LSTM记忆块结构。

利用LSTM网络预测转炉炼钢终点碳温时，图3中的记忆模块在第T炉次预测终点碳温的计算过程如下：

(11)

it=σ(wxixt+whiht-1+wcict-1+bi);

(12)

ft=σ(wxfxt+whfht-1+wcfct-1+bf);

(13)

ot=σ(wxoxt+whoht+wcoct+bo);

(14)

(15)

ht=ot·tanhct。

(16)

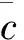
2.2 转炉炼钢终点碳、温预测模型的建立步骤

本文终点碳温预测模型建立流程如图4所示，具体建模步骤如下：

步骤1获取历史样本训练集。将传感器采集的BOF转炉炼钢过程生产数据进行数据清洗和特征选择后得到历史样本库。

步骤2获取待测样本的初始训练样本集。通过GRA准则[20]计算待测样本和历史库样本FOS值，选择阈值在0.8以上的相似样本，得到初始样本矩阵SP×M。

步骤3选择质心样本。通过GRA准则得到初始样本矩阵SP×M两两之间的FOS值，并降序排序得到对应的索引值矩阵，将获得的最大FOS值样本作为质心样本。

步骤4获取待测样本的最终训练样本集。二次计算质心样本与历史样本库的FOS值，选择GRA值在0.8以上的样本，得到最终待测样本的训练样本库Sd×M。

步骤5预测模型。将得到的最终待测样本的训练样本库Sd×M输入改进的LSTM网络中进行训练，输出待测样本的终点碳、温值。

3 仿真实验

按照上述方法建立转炉炼钢终点碳温预测模型，用30组数据进行预测实验，为证明本文方法在预测精度上的有效性和模型抗干扰能力，分别用JITL+LSTM模型、改进JITL+LSTM模型、JITL+改进LSTM模型、数据扰动下的改进JITL+改进LSTM模型与本文方法进行终点碳温预测对比实验，同时与文献[17-19]进行横向对比。

3.1 实验原始数据和样本特征

实验数据来源于实际钢厂转炉炼钢生产数据，其过程数据包括装入铁水量、装入生铁量、装入废钢量、铁水C、铁水SI、铝铁时间、1吹氧量、枪位16、氧压28等120维数据，历史库样本2万炉次。将原始实验数据进行抽象，如表1所示，其中温度的单位为℃，碳含量的单位为百分比含量。

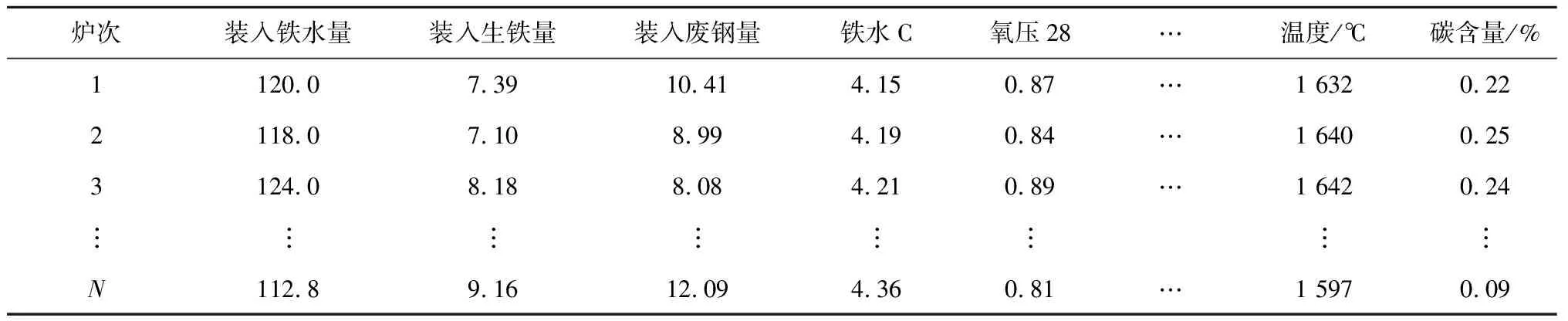
表1 转炉炼钢生成过程原始数据

通过特征选择选出终点碳、温与生产过程数据联系最密切的特征，如表2所示。其中：终点温度预测的输入特征包括氧压31、兑铁时长、兑铁结束到开氧时间、铁水温度、枪位36、装入废钢量；终点碳含量预测的输入特征包括装入生铁量、铁水P、枪位22、氧压29、氧压11、枪位16。

表2 终点碳、温预测模型的输入特征

3.2 终点碳温预测实验

为证明本文算法的有效性，进行5组对比实验。以终点碳温的预测精度为评价指标，对比实验结果如表3和表4所示，其中：表3为终点温度预测的精度，给出了±10℃和±5℃时模型的预测精度；表4为终点碳含量的预测精度，给出了终点碳含量预测时误差在±1个碳(0.01%)和±2个碳(0.02%)的预测误差精度。

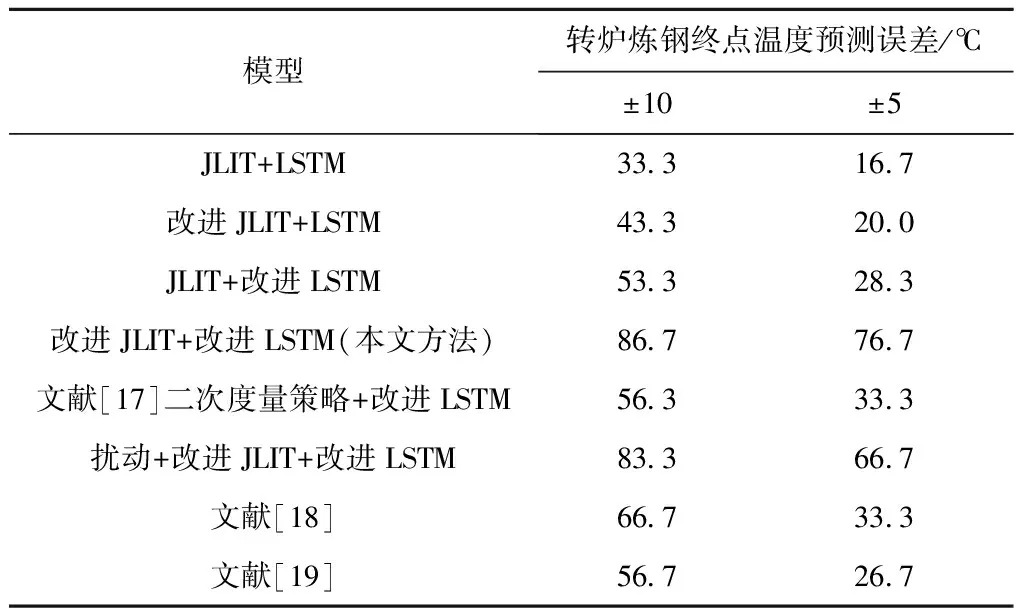
表3 终点温度模型预测结果 %

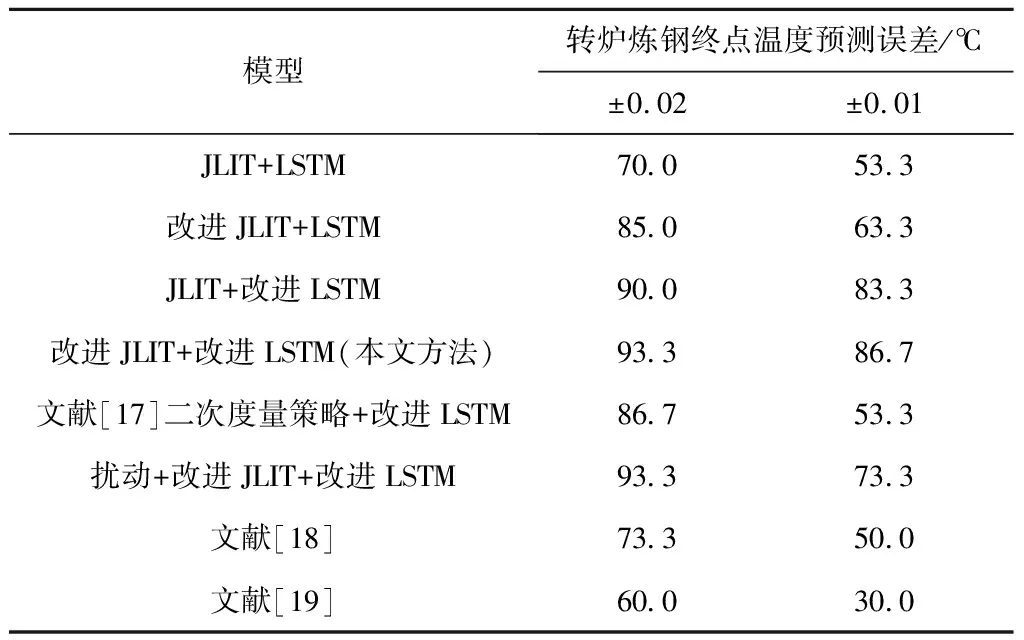
表4 终点碳含量模型预测结果 %

(1)对比实验1，为证明QOS度量策略的有效性，将改进JITL+LSTM模型与JITL+LSTM模型进行对比，如图5～图8所示。

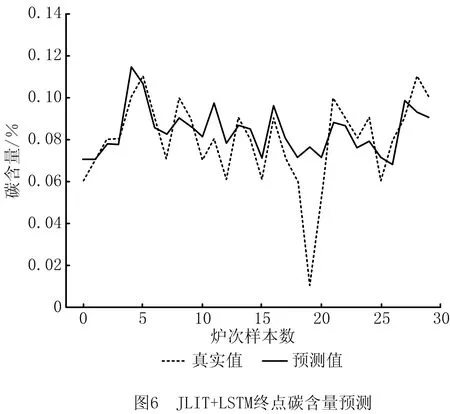
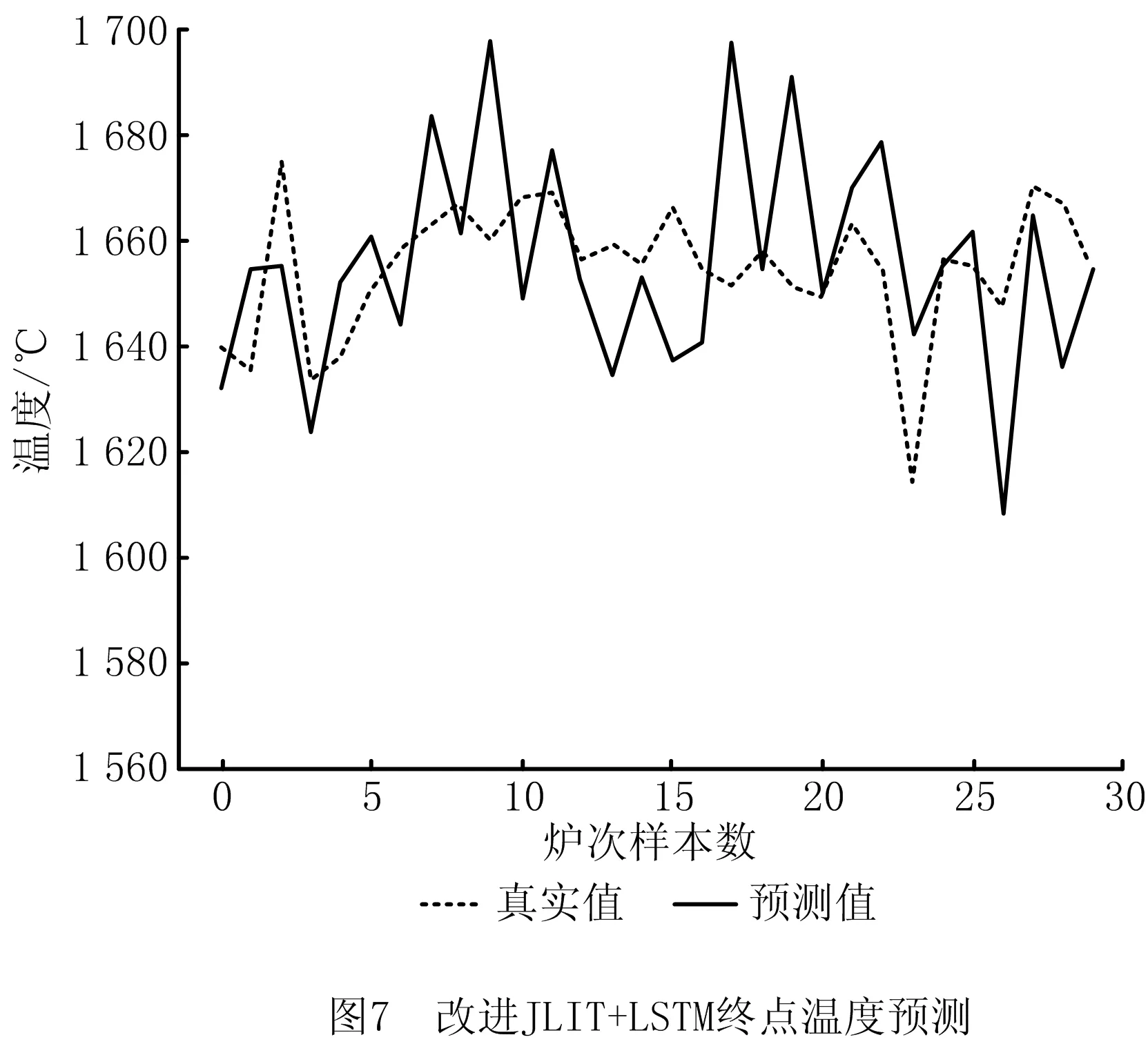
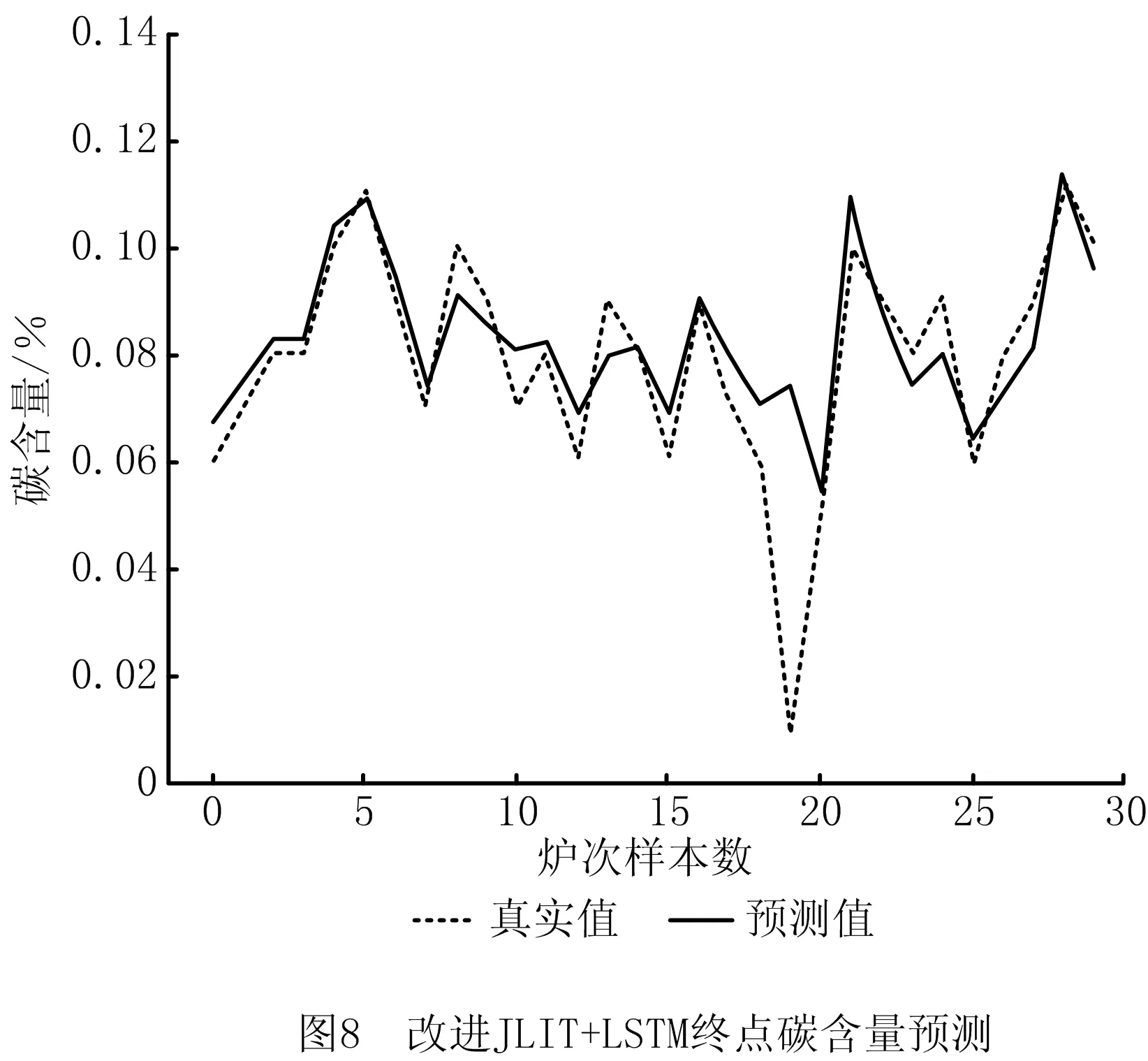
(2)对比实验2，为证明带有反馈补偿的改进LSTM网络的有效性，将JITL+LSTM模型与JITL+改进LSTM模型进行对比，如图5、图6、图9、图10所示。

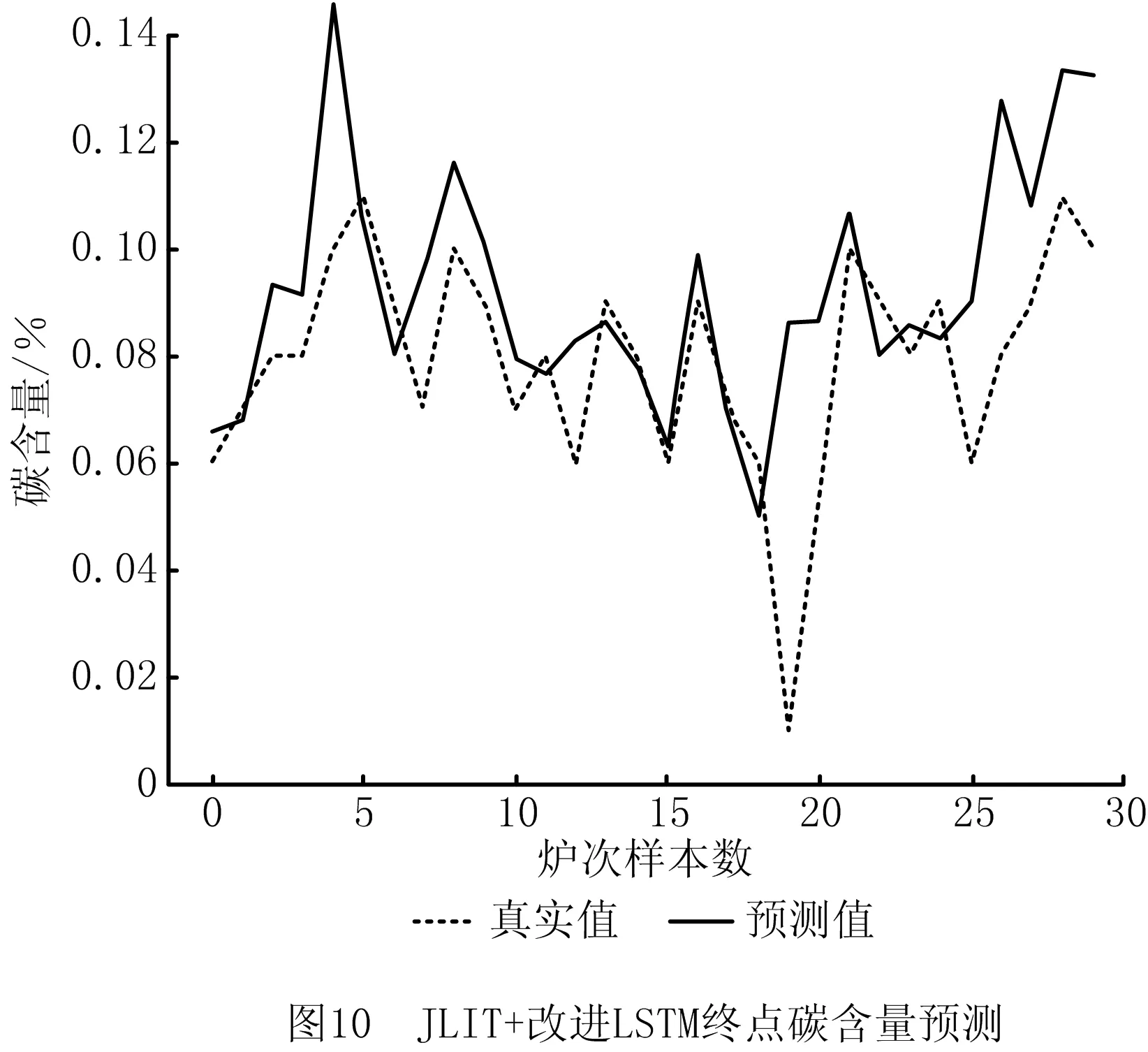
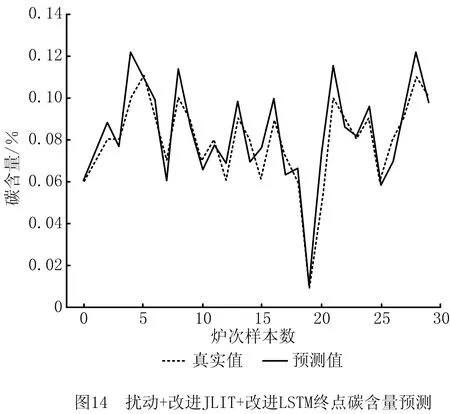
(3)对比实验3，图11和图12所示为本文所提方法的实验结果。为证明本文所提方法具有较强的抗干扰能力，将本文方法(改进JITL+改进LSTM模型)应用于异常波动的数据终点碳温预测，结果如图13和图14所示。

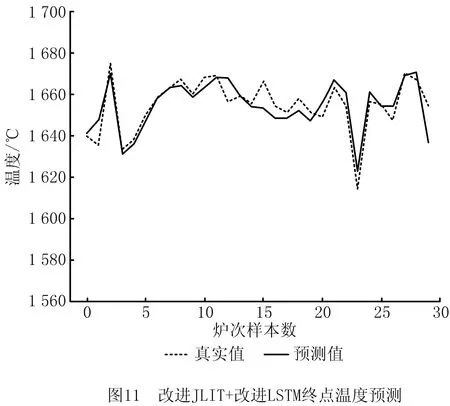
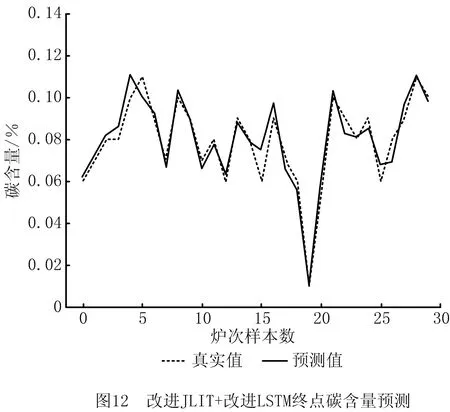
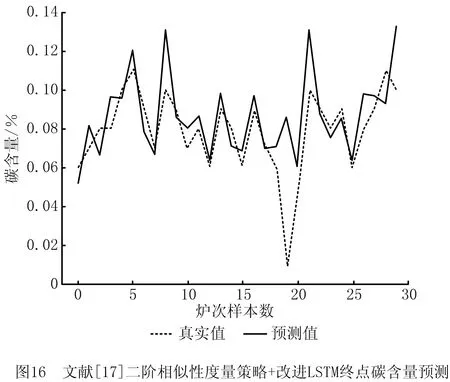
(4)对比实验4，为证明本文QOS度量策略优于文献[17]中的二阶相似性度量方法，采用文献[17]中的二阶相似性度量方法并结合与本文方法相同的预测模型进行实验，也即实验将两种度量策略得到的样本统一采用改进的LSTM网络进行对比，结果如图15和图16所示。

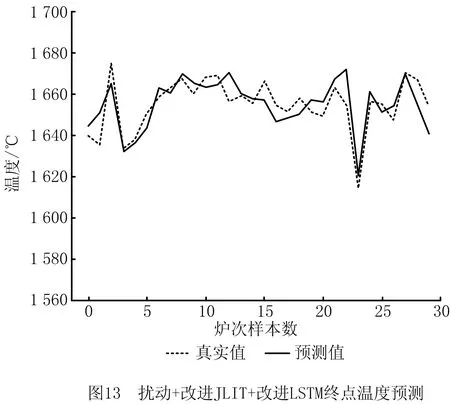
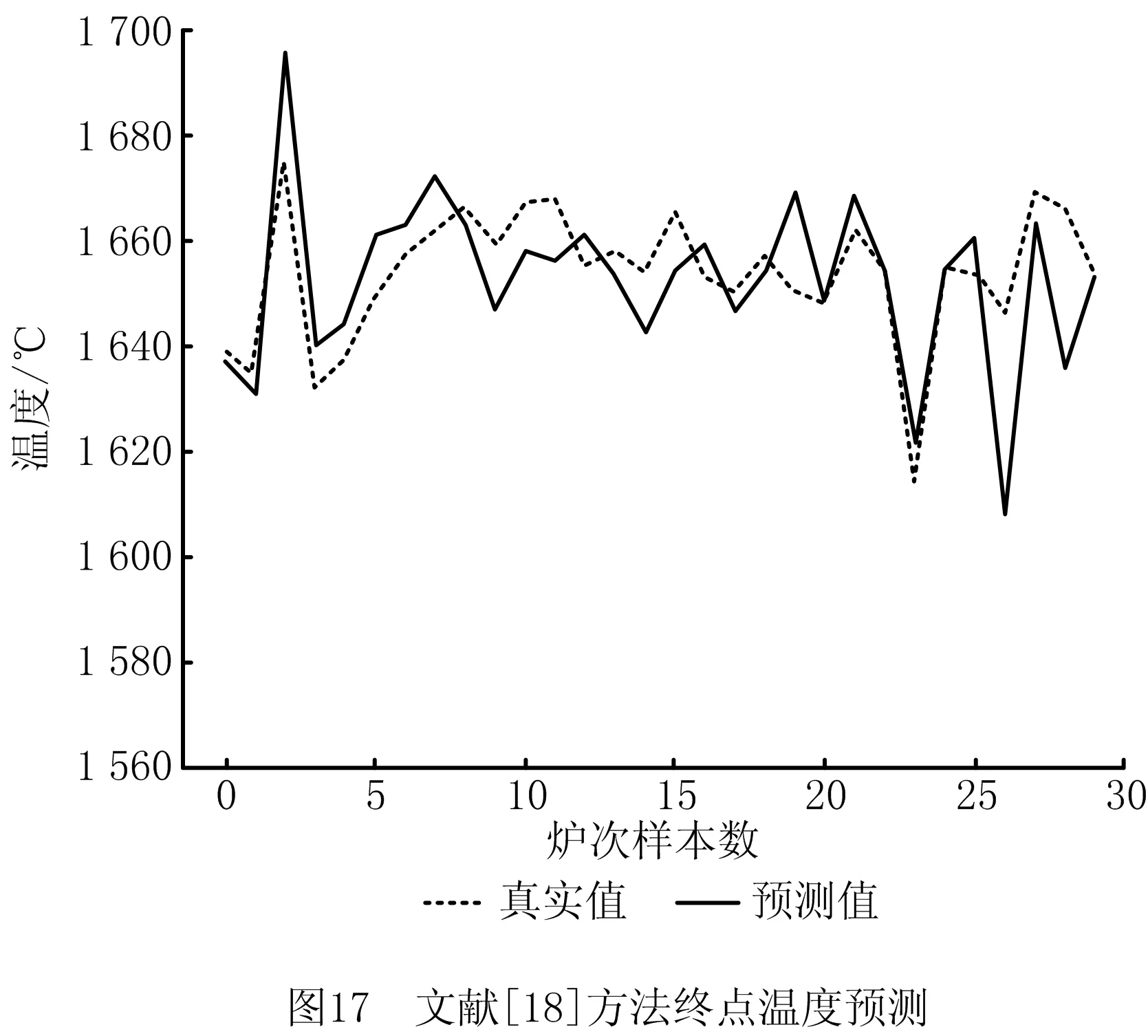
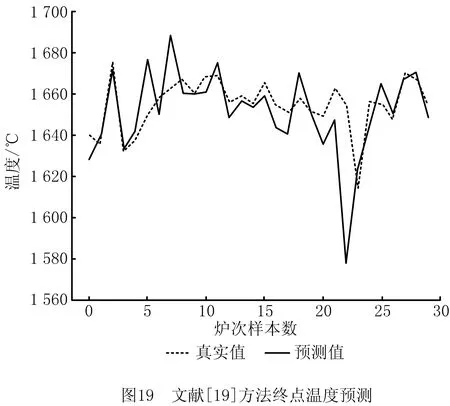
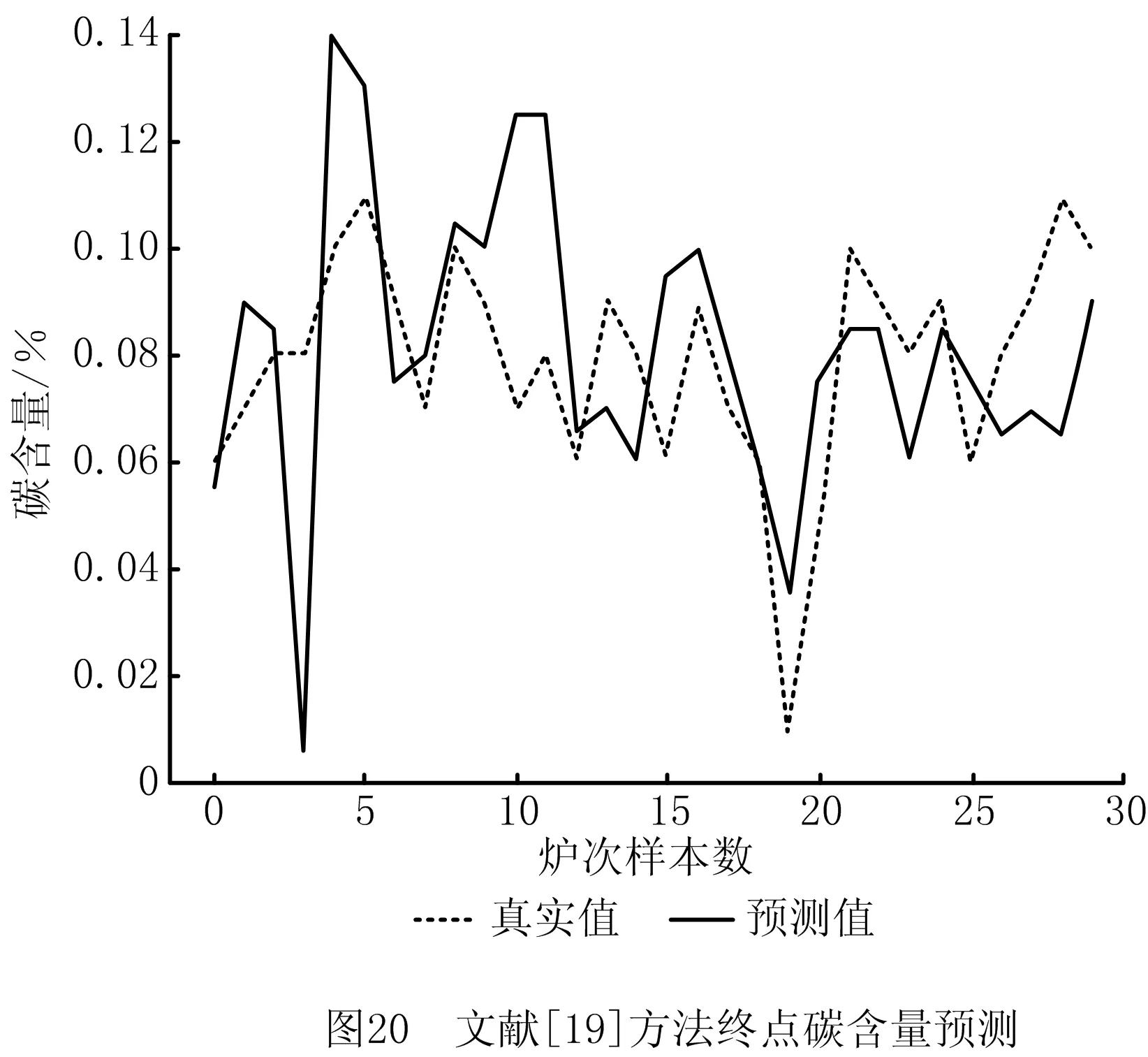
(5)对比实验5，为证明本文所提方法在碳温预测精度上的优势，引入文献[18-19]的方法预测终点碳温进行横向对比实验，结果如图17～图20所示。

3.3 实验分析

通过分析实验结果，在对比实验1中，JITL+LSTM模型与改进JITL+LSTM模型，预测温度在±10℃的精度从33.3%提高到43.3%，碳含量预测误差在±0.02内的精度从70.0%提高到85.0%。这是由于本文方法所采用的QOS度量策略在选择质心样本的基础上提出二次度量机制，并考虑了样本的整体特性和时间序列信息，使局部样本的选择更加合理，证明了本文QOS度量策略的有效性。

对比实验2中，JITL+LSTM模型与JITL+改进LSTM模型，预测温度在±10℃的精度从33.3%提高到53.3%，碳含量预测误差在±0.02内的精度从70.0%提高到90.0%，精度提升约15%。原因是改进后的RNN不但可以提取层次间的特征，而且加入的反馈层融合了炉次样本间的序列特征，从而充分利用T-1炉次信息，有效提高了模型预测精度。

对比实验3中，在数据有干扰的情况下，预测温度在±10℃的精度为83.3%，在±5℃的预测精度为66.7%，相比无干扰的情况分别下降了3.4%和10%；在误差允许范围内，碳含量预测中，±0.02的预测精度为93.3%，±0.01的预测精度为73.3%，相比无干扰的情况，误差在±0.02时保持不变，在±0.01时下降了13.4%。该组对比实验证明本文所提方法具有一定的抗干扰能力，原因是QOS度量策略使选择的局部样本时间序列信息更强，而且改进的LSTM网络有效融合了邻近样本信息，在数据异常时可以有效忽略其干扰，增强了模型的鲁棒性。

相比于文献[17]，本文所提方法的预测温度在±10℃的精度从56.3%提高到86.7%，碳含量的预测误差在±0.02内的精度从86.7%提高到93.3%。该组对比实验证明本文方法选择的局部样本优于文献[17]方法，原因是本文采用灰色关联度指标时有效挖掘出了炉次样本的时间序列信息，同时质心样本的确定解决了更高阶情况下的样本漏检问题，使其局部样本类内和类间分布更佳。

文献[18-19]的实验结果中，温度预测误差在±10℃时的精度分别为66.7%，56.7%，碳含量预测误差在±0.02内的精度为73.3%，60.0%。实验结果表明，采用本文方法预测转炉炼钢生产过程数据的终点碳温更具优势。

通过实验结果分析，本文提出的QOS度量策略能够实现终点碳温软测量方案，所建立的局部模型使终点温度预测精度提高了10%，使终点碳含量的预测精度提高了约15%，说明改进的终点碳温即时学习能兼顾样本的全局性，使待测样本的训练样本集合相似性更高，同时改进的LSTM使终点碳温的预测精度提高了20%，证明了改进方法的有效性；而且在样本数据有干扰的情况下，模型的预测精度在误差允许范围内，证明了本文所提二次度量策略+改进LSTM模型具有一定的抗干扰能力。

4 结束语

转炉炼钢过程中，终点碳温准确预测是影响钢铁质量的关键。本文针对转炉炼钢过程数据具有炉次间的时间序列特性以及样本间数据波动较大的问题，建立QOS度量策略的终点碳温软测量方案，以及带有反馈补偿机制的改进LSTM网络模型进行终点碳温预测，具体内容如下：

(1)采用GRA准则进行第一次度量，建立初始待测样本的训练集，确定质心样本，然后进行二次度量获取最终的训练集样本库，使训练集样本类内方差总和最小，进而获取最佳训练样本。

(2)改进的LSTM网络使隐含层和输出层的特征使用得更加合理，循环隐含层可以提取层次间的特征，加入反馈层融合了炉次样本间的序列特征，使在数据残缺时充分利用上一炉次的信息，从而保证其预测精度最优。

本文所提终点碳温预测模型具有一定实用价值，为实现计算机自动控制转炉炼钢奠定了基础。