再制造机床装配过程误差传递模型与精度预测

王子生，姜兴宇，刘伟军，石敏煊，杨世奇，杨国哲

(沈阳工业大学 机械工程学院，辽宁 沈阳 110870)

0 引言

作为机床再制造过程中的最后一环，装配直接决定了组装产品的性能和质量。由于机床零件的尺寸及其在装配中的位置不同，各零件对整体产品装配精度的影响程度不同，如何定量描述这些影响，制定相应零件装配精度的要求，从而降低装配成本，保证装配质量，是亟需解决的问题[1]。

与新机床不同，再制造机床在装配过程中使用了大量的再制造零件，由于工艺不同，再制造零件的公差带离散程度较大[2]，必然会产生由零件不确定性和随机性引起的装配偏差。偏差随工位的传递不断累积，最终对再制造机床整机的性能和质量产生影响[3]。而目前传统的装配偏差分析方法一般认为装配偏差为正态分布，仅能计算大批量制造的新零件的偏差分布规律，不适用于再制造机床零件装配。因此，为保证再制造机床装配的精度与质量，降低误差影响，迫切需要一种能够有效对再制造机床装配过程的尺寸偏差进行描述、检测和控制的定量分析方法。

目前针对制造过程的误差累积问题，国内外学者进行了深入研究。在生产过程误差方面，国外Lawless等[4]研究了制造过程中的偏差传递，提出一种基于时间序列分析的自回归模型，并用统计模型反映加工过程偏差的传递规律；Lewis等[5]结合稳健性设计和统计过程控制，针对产品设计阶段考虑其误差控制方式，解决了多种工艺加工的偏差问题；Zuo等[6]提出一种集变异和多目标优化方法，通过分解机械加工过程实现误差源的逐级识别与多目标精度分配，减少了与灵敏度相关的成本和误差；Huang等[7]提出一种基于误差预测的机床精度设计方案，完成了机床部件的精确分配和精度检测；阎艳等[8]建立了基于矩阵微分法的几何误差对装配精度的灵敏度分析模型，为精密装配的误差分析及精度控制提供了理论基础。

针对再制造过程的不确定性和随机性误差问题，国内学者进行了大量研究。刘明周等[9]对再制造过程偏差的产生和传递机制进行了综合分析，基于装配偏差度理论提出一种针对复杂机械再制造过程的误差修正方法，并基于模拟退火遗传算法，设计了装配偏差度修正模型，并对复杂机械产品再制造装配过程的质量进行了优化；刘明周等[10]针对机械产品再制造装配过程的质量控制问题，提出一种面向机械产品再制造装配过程的动态工序质量控制模式，并构建了一种面向机械产品再制造装配过程动态工序质量控制系统的功能结构模型；姜兴宇等[11]针对废旧件再制造过程波动性大、加工时段不连续等问题，提出一种基于动态、非正态分布指数加权移动平均值(Exponentially Weighted Moving-Average, EWMA)控制图的再制造过程质量控制方法，在此基础上构建了面向动态、非正态分布的再制造过程质量EWMA控制图，实现了动态再制造过程质量的自适应监控；马浩等[12]综合考虑产品加工过程装夹造成的夹具误差与基准误差，以及机床本身的几何运动误差，建立了一个整合的误差数学模型，从生产系统全局的角度对生产误差进行了综合分析。

在产品装配过程误差研究方面，Zhang等[13]通过普通最小二乘理论推导出偏差误差的数学机制和预测模型，推断出高精度传递对准中的偏差误差；赵家黎等[14-15]采用状态空间方程阐述了多工序装配过程的产品结构和特点，建立了基于误差流理论的多工位装配制造过程误差传递基本模型；余德忠等[16]研究多工位装配工艺，并采用状态空间法建立装配尺寸误差模型，减小了装配尺寸误差；余璐云等[17]为了诊断加工误差，控制加工精度，提出一种集成尺寸误差模型和质量监控策略；陈根良等[18]对闭环、开环和并联机构进行分析，建立了统一的误差传递模型；李界华等[19]针对多工位装配过程，提出一种基于偏差传递的质量评估和预测模型，量化了多工位装配过程的装配质量；蔡尚文等[20]针对各个零件加工和装配过程中的误差累积情况，建立了基于小位移量理论的零件装配误差传递模型，并对其进行了描述。

综上所述，目前误差的研究主要集中在对新产品制造过程中误差传递规律的分析，鲜有对再制造产品装配过程误差进行分析和修正。新机床制造过程的偏差主要来源于装配零件在不同工位之间转换，极易造成重定位偏差。而再制造机床由新件、再利用件、再制造件装配而成，不同类型零件的尺寸公差范围较大，混合装配时产生的配合偏差也是导致偏差质量问题的重要原因。在再制造装配过程中，由于缺乏对应的偏差预测模型，无法得到各工位的输入误差，装配人员不能直观地获得装配信息，使修正装配误差比较困难，也容易在各工位之间积累装配偏差。

为了能够有效描述并解决再制造装配偏差积累问题，本文研究废旧机床装配过程中的误差传递和积累规律，提出基于状态空间模型的再制造机床装配过程误差分析与修正方法，建立了废旧机床再制造装配过程误差流模型，并通过该模型和现场测量数据分析，推导出相应的误差流修正函数，为再制造机床的综合装备精度预测、分析和质量误差修正奠定基础。

1 再制造机床装配过程的误差传递机理

再制造机床装配零部件中大量使用再制造件和修复零件，其尺寸公差波动范围较大，降低了再制造机床的质量稳定性。机床再制造装配过程可看作为一个多输入和多输出的一维离散时变系统，质量属性以再制造零件为载体，沿各个装配工序动态累积、耦合和传递，形成装配过程偏差流，最终对产品装配质量产生影响，导致装配质量不确定、不稳定。

因此，本文采用状态空间法建立再制造机床装配过程的质量模型，在详细分析再制造机床装配过程各种影响因素的基础上，以各个工位装配工人的实际操作和零件自身质量属性为输入向量，再制造产品的装配精度为输出向量，建立再制造机床装配的状态空间模型，研究再制造机床装配质量的优化控制机制。图1所示为再制造装配过程中各个工位装配精度被装配过程噪声φi和输入误差μi影响，导致产品的零件特征尺寸xi随装配工位不断变化导致的偏差传递和积累过程。

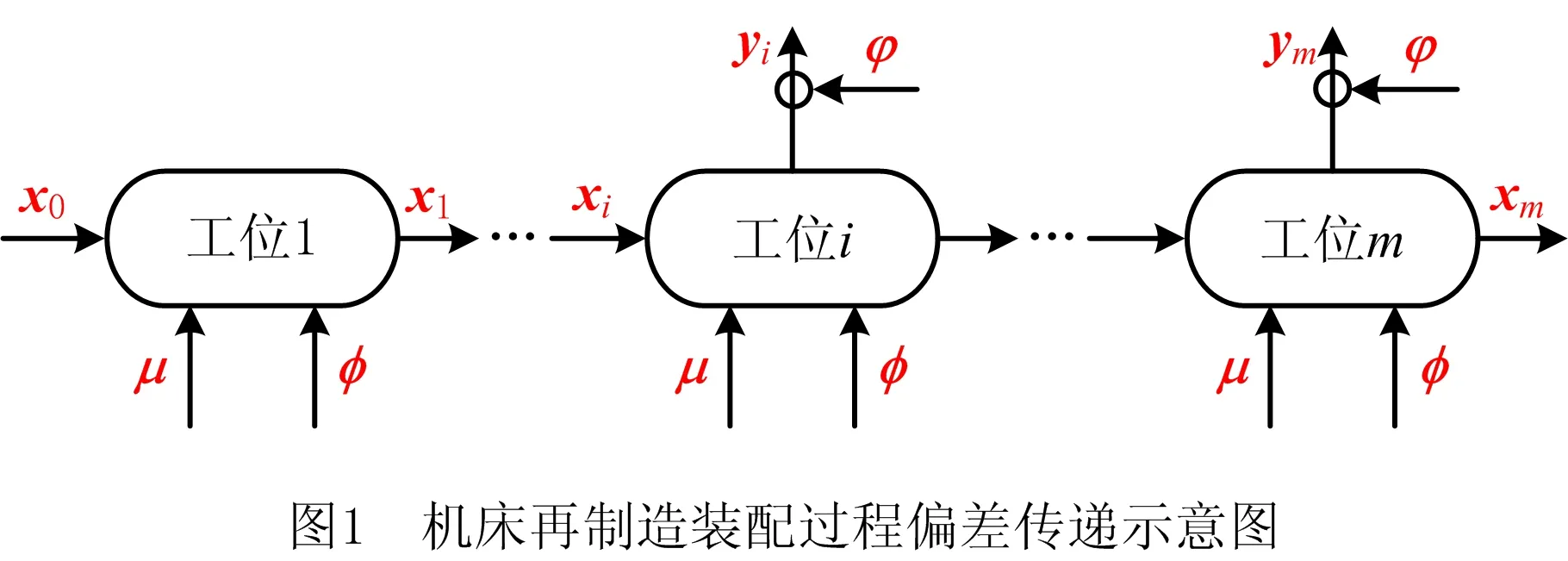
2 基于状态空间模型的再制造机床装配过程误差流模型

2.1 误差流模型及零件模型的构建

假设再制造机床某装配体的装配过程分为M个工位，在M工位装配过程中，每个单独工位只对一个质量合格的零件执行装配工作。状态空间方程可以描述一维离散时变系统，而装配工序完全符合一维离散时变系统的特征，因此在忽略噪声的理想情况下，再制造机床装配体的装配过程状态空间方程如下：

(1)

式中：i表示装配工位，i∈(1,2,…,M)；xi表示经过i个工位后，零件特征尺寸(即再制造机床装配体)的状态；yi表示经过第i个工位后产品质量特征的名义值；Ai为系统状态转换矩阵，表示两个连续工位i+1与i之间的关系；Ci为观测矩阵，表示装配体中质量特征的实际值与理论值之间的对映关系，当某工位没有测量工序时为零矩阵。

因为再制造零件的质量偏差较大，实际再制造装配过程中存在系统误差和随机误差，所以引入针对再制造过程的噪声因子，得到状态空间方程：

(2)

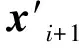
将实际加工过程中产生的输入误差、装配过程噪声、控制噪声等导入理想状态下的空间方程，即将式(2)与式(1)相减，得到多工位装配过程误差传递模型：

(3)

设装配过程的状态传递矩阵为Di,j，对Di,j有如下定义：

(4)

为了更直观地得出系统输出与输入之间的关系，将式(3)进行整理转换：

(5)

用其他符号表示式(5)中的各矩阵：

(6)

(7)

(8)

整理后可将式(5)转化为

yi=Hx0+Eμi+K。

(9)

在装配再制造机床时，ωi为测量噪声和生产噪声对最终产品质量的影响程度，假设在同一类装配过程中，ωi为常数，即K为常数，x0为再制造零件装配过程中的系统初始误差。

为了更清晰地描述装配偏差的传递和积累规律，本文对再制造机床装配过程的输入输出向量表达方法进行了深入研究。再制造机床的装配过程中，作为装配过程的基本单元，零件的工作面质量和质量特性是影响产品最终质量的关键因素，因此将零件基本单元作为装配过程输入向量的参照。

在同一类装配过程中，设参与装配的一个零件有n个面与装配过程有关，这n个面包括工作面及与其他零件保持位置特征关系的面。如图2所示，在零件坐标系中，第i个面的状态可以通过该面的位置矢量Pi=(Pix，Piy，Piz)Τ、方向矢量Oi=(Oix，Oiy，Oiz)Τ和质量特性Fi=(Fi1,Fi2,…,Fim)Τ共同表示，将Oi，Pi，Fi3个矢量合并表达一个矢量Ui，

(10)

式中m为零件第i个面的质量特性(包括尺寸、形状位置等质量特性)数量。

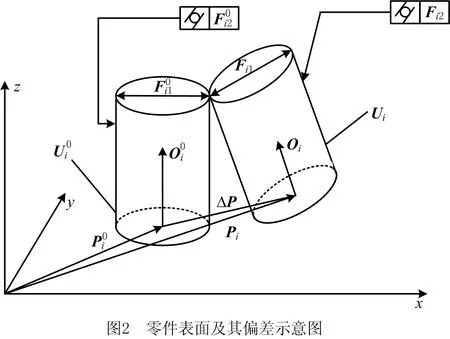
图2所示为零件理论位置和实际位置之间的偏差形式，表示零件某一工作面的状态和偏差可由其位置矢量、方向矢量和质量特性共同表示。再用一个矢量表示零件的所有工作面，得到该零件的状态矢量为

(11)

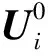
(12)

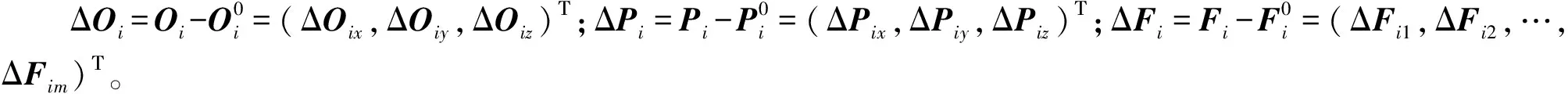
由式(11)和式(12)得到零件偏差

(13)

2.2 再制造装配过程的误差修正函数

装配系统输入向量μi包括零件自身属性输入μip和操作输入μio，μip在装配开始前的选配过程中就已经确定，在整个装配过程中无法更改；操作输入μio由装配过程操作引入，如果实际装配零部件的质量特性无法满足预先装配要求，可以在装配过程中根据实际装配情况适当调整操作输入向量值来修正误差，改善装配精度，提升装配体质量。

μi=μip+μio。

(14)

将式(14)带入式(9)，重新整理后得到新的误差流函数

yi=Hx0+E[μip+μio]+K。

(15)

由于式(15)中x0系统的初始误差为0，且K为常数，可以通过调整μio使最终装配质量满足预期要求。通过转换得到装配过程的误差修正函数

μio=[yi-K]E-1-μip。

(16)

当装配产品的质量特性超出标准范围时，可以采用装配过程误差修正函数指导再制造机械产品装配的误差修正，从而优化控制再制造产品的装配精度。

2.3 再制造装配过程的状态空间模型

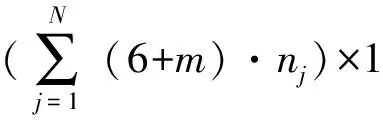
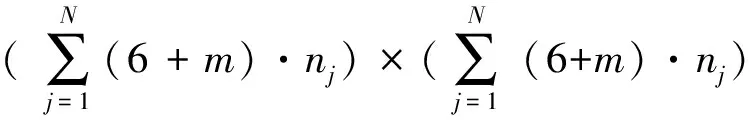
在再制造装配过程中，装配偏差由零件加工偏差引起，其传递方式如图3所示。

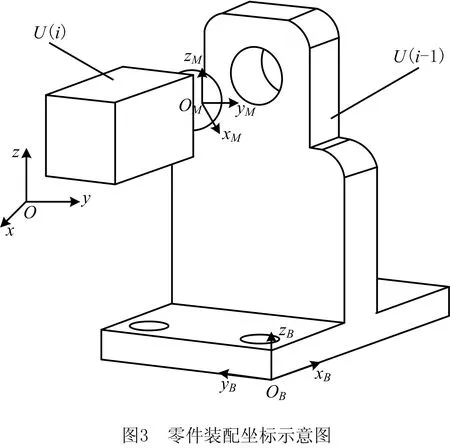
图中，Oxyz为零件坐标系，在制造和测量零件时使用，该坐标系中用U表示零件；OMxMyMzM为配合坐标系，因加工误差，配合坐标系一般与零件坐标系不一致，该坐标系中用UM表示零件；OBxByBzB为基础坐标系，是装配体的参考坐标系，该坐标系中用UB表示零件。

从偏差传递的角度看，零件的装配过程分为两种形式：①由于待装配零件自身加工误差导致其零件特征由零件坐标系向配合坐标系转换时产生的零件偏差；②在配合坐标系中，零件配合部位特征向基础坐标系转换时产生的安装偏差。

零件特征在坐标系中变换时有平移和旋转两种形式，分别用R和T表示，则零件装配过程可以表示为：

(17)

(18)

(19)

(20)

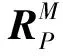
式(17)和式(18)表达了再制造装配过程中，零件特征从零件坐标系到配合坐标系，再到基础坐标系的转换过程。在数学上，这一过程可以合并，使零件特征从零件坐标系直接转换到基础坐标系，即

(21)

(22)

式中θp×q为p×q维零矩阵。

观测矩阵

(23)

式中Ci(i)为ti×[(6+m)·ni]维矩阵，表示在装配体中第i个零件的质量特性实际值与观测值之间的映射关系。

2.4 装配过程误差修正模型的应用流程

根据前面理论，构建基于误差流传递模型的再制造机床装配过程质量优化方法的流程，如图4所示。

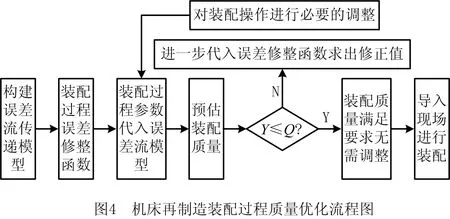
(1)在充分研究再制造机床装配过程质量及影响因素的基础上，设整个装配过程有N道工位，将这些工位联合起来看作一个时间序列，视为一维时变系统，并采用状态空间方程进行描述，从而构建误差流传递模型，同时根据现场实测数据计算出误差流传递模型中相应的矩阵参数A，B，C。

(2)对误差流传递模型进行变换，推导出装配过程误差修整函数。

(3)基于装配过程误差修整函数，将装配参数带入误差流模型中进行求解，预估装配后的产品质量。

(4)比较预估装配产品质量误差Y和误差标准值Q，如果不满足要求，则计算误差修整函数值，在对其进行必要修整后，再进入误差流模型，循环往复，直到装配产品质量满足要求；如果产品装配质量满足要求，则无需对装配过程进行调整，直接将数据导入现场进行装配，装配质量优化流程结束。

3 应用实例

3.1 再制造机床主轴箱装配过程的关键影响因素

本文以再制造机床主轴箱装配为例，对主轴的装配精度进行控制。通过详细划分再制造机床主轴箱的装配工艺流程，探究装配质量的关键影响因素，对其装配精度进行预测，并采用误差传递模型修正装配误差。工艺流程分解后得到的主轴箱内各个工位上零件的装配初始向量、装配过程向量和输出向量如表1所示。

表1 机床主轴箱各装配工位影响参数表

3.2 再制造机床主轴误差修正模型

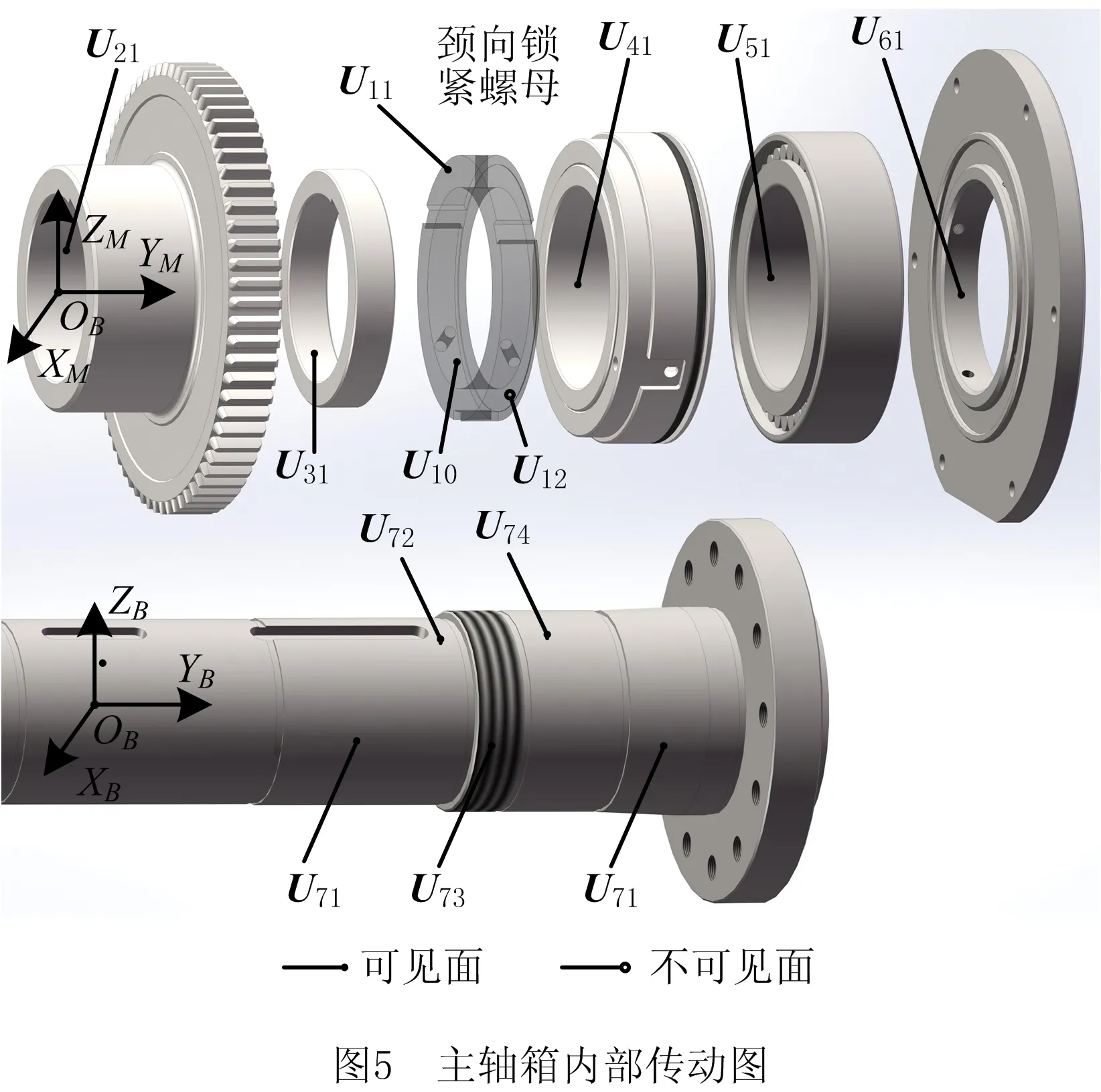
由表1可知，在主轴装配过程中，各零件装配的实际位置和理论位置的误差主要表现为主轴的径向跳动。本文以主轴装配为例，以主轴的径向跳动为关键质量控制点，对再制造机床误差进行修正，主轴箱零件装配后的内部传动如图5所示。由表1知主轴装配零件的装配输入初始向量包括锁紧螺母理想装配位置、隔套理想装配位置、锁紧螺母的厚度及隔套的厚度；过程变量包括锁紧螺母的实际位置、隔套的实际位置；最终的装配输出变量为主轴的径向跳动。根据实际经验可知，作为主轴装配的关键零部件，锁紧螺母的装配误差对主轴径向跳动会产生巨大影响，因此本文选择以锁紧螺母的装配位置为研究对象进行误差修正。

为了在实际的主轴生产装配过程更加实用，建立了一个简化的主轴内部传动模型。将锁紧螺母螺进距离作为装配过程的补偿，通过将调节锁紧螺母螺旋进度作为输入来保障主轴的稳定性。

再制造主轴误差修正流程如下：

(1)将三坐标测量仪测得的锁紧螺母实际输入参数和标准质量要求的装配输入初始理论参数代入再制造主轴装配过程的误差流分析模型，推导出装配过程输入向量的修正值。

(2)根据修正值选取最接近的锁紧螺母修正对应的螺进距离，根据径向跳动的数值差异选择补偿不同的螺进距离，如表2所示。

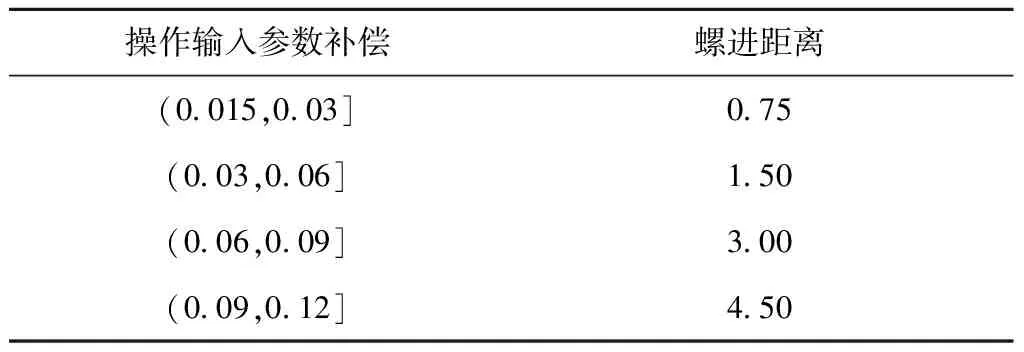
表2 锁紧螺母输入操作参数补偿表 mm

(3)根据表2的区间范围选取径向跳动参数值落在区间范围内对应的螺进距离，使再制造机床主轴装配过程中的径向跳动参数预测值满足要求。

(4)将修正后的输入向量代入装配过程误差流模型，如果计算得到的装配过程向量和输出向量满足系统要求，则进入下一工位。

根据式(3)推导出再制造装配过程锁紧螺母工位的误差流模型为：

(24)

基于再制造机床装配车间的多工位装配过程历史数据，并参照文献[15]计算可得误差流模型中的系统状态转换矩阵A、控制矩阵B和观测矩阵C：

表3和表4所示分别为锁紧螺母零件特征面的装配输入初始理论参数与采用三坐标测量仪测得的锁紧螺母零件特征面的实际状态参数。因为质量控制参数是特征面U11和U12的径向跳动，其与特征面的位置矢量和方向矢量密切相关，而与特征面自身的尺寸变形无明显关系，所以令m=0，即在计算过程中忽略质量特征参数的影响。

表3 锁紧螺母装配输入初始理论参数

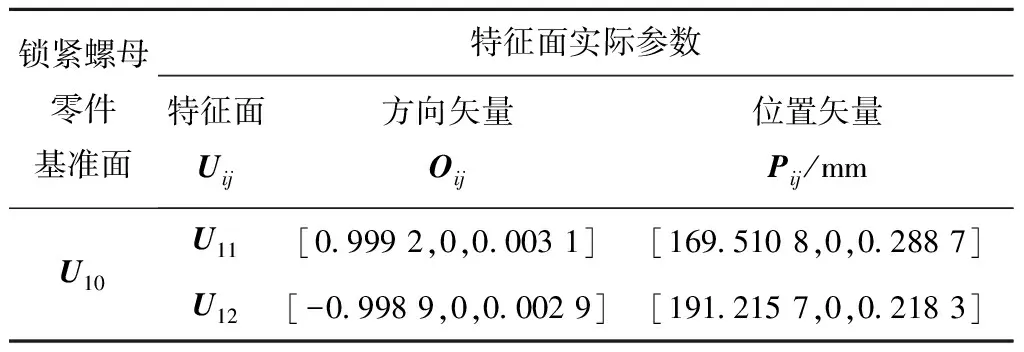
表4 锁紧螺母装配过程的实际状态参数

忽略装配过程中的环境噪声、零件微量变形，测量误差等动态不确定性的影响，用μ1表示实际装配过程中的输入误差，计算得到μ1=(-0.001 9 0 0.000 2 0.295 1 0 0.196 8)Τ。

将装配过程中测得的实际状态参数代入再制造主轴误差流修正模型式(17)。由于只需计算锁紧螺母径向跳动误差，取，通过采用误差流优化模型推导出的输出向量待修正参数值，即径向跳动值y1=0.047。对比主轴径向跳动误差标准值，输出结果如表5所示。

表5 装配输出向量值 mm

表5表明，通过误差流优化模型计算得到的径向跳动值为0.047 mm，超出企业误差标准值0.02 mm，需要进行修正。根据表2对装配过程进行正向修正，查表可得修正的螺进距离应为1.5 mm。修正后再次使用三坐标测量仪测量出锁紧螺母零件的实际状态参数，测量结果如表6所示。

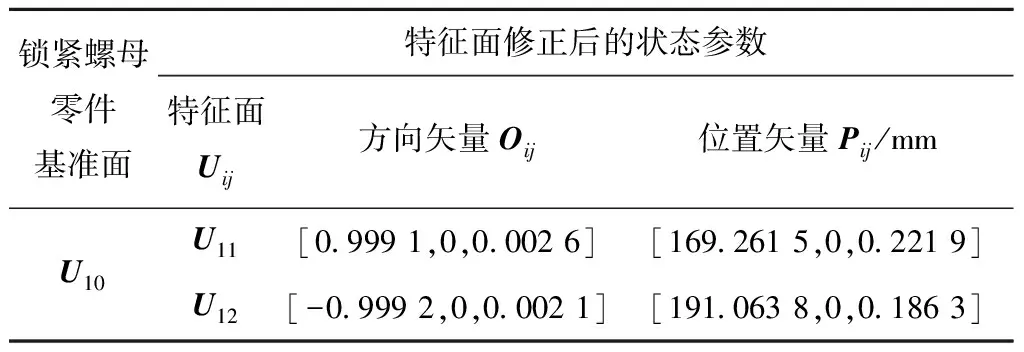
表6 装配修正后的状态参数

将修正后的实际状态参数代入式(17)，求得输出向量参数值，然后采用三坐标测量仪检测修正后主轴的实际装配数值，对比结果如表7所示。

表7 修正后的输出向量对比值 mm

通过误差修正模型得到的修正后的锁紧螺母径向跳动值为0.012 mm，修正后测得的实际径向跳动值为0.013 mm，低于企业规定的误差标准。以上实例说明了基于误差流模型的再制造机床质量优化方法的有效性和可行性，其能够很好地对再制造机床主轴装配误差进行有效优化。

4 结束语

本文建立了一种基于再制造的多工位装配过程的零件误差流修正模型和基于质量偏差的再制造零件模型，该模型考虑了零件在三维空间中的位置、方向和质量参数，以一种新的方法和途径对质量参数进行了定量表达，同时针对再制造零件实际尺寸偏差较大，装配过程噪声严重的问题，提出再制造机床装配的质量优化流程图，为再制造装配过程中的零件选配方法和误差修正方法提供了思路。最后以再制造机床主轴箱装配为例，验证了本文所提误差传递模型和误差修正函数的有效性，为提高再制造机床主轴箱装配质量提供了理论支持。

为了提高误差流传递模型的运行效率和实用性，本文简化了装配过程误差流传递模型的部分向量。未来工作将结合实际数据，采用统计学的相关理论对该模型进行完善。