考虑物料装卸点与搬运通道的多行设施布局
董舒豪,徐志刚+,常艳茹,秦开仲,朱建峰,苏开远
(1.山东大学 机械工程学院,山东 济南 250061;2.山东大学 深圳研究院,广东 深圳 518057)
0 引言
设施布局是将若干作业单元合理地布置在给定的空间内,布局方案形成后,将对企业的生产成本、在制品、交货期、生产效率、工作环境等产生重要影响,关系到企业能否充分发挥其经济效益与社会效益[1-2]。因此,设计出合理的设施布局方案对企业生产运营尤为重要。
设施布局问题因其有重要性与复杂性而受到国内外众多学者的广泛关注与研究。当前设施布局问题的研究多是首先构建出布局优化模型,然后采用智能优化算法求解,常见的算法有遗传算法(Genetic Algorithm, GA)[3]、蛙跳算法[4]、模拟退火(Simulated Annealing, SA)算法[5]、蚁群算法[6]、粒子群算法[7],还有一些较新型的算法应用在设施布局中,如殖民竞争算法[8]、萤火虫算法[9]、随机生长算法[10]等。设施布局模型的准确性和真实性是采用算法求解并获得有效布局方案的前提,文献[3-10]的布局模型中将物料装卸点的位置定义在作业单元的中心点,然而实际生产中,作业单元的面积、物料装卸点位置各不相同,因此假定物料装卸点处于作业单元中心的布局模型在反映实际情况时具有一定局限性。Das[11]提出一种布局模型,模型中装料点与卸料点在同一位置,并限制在作业单元的中心线上;Kim等[12]、Xiao等[13]对前述布局模型中的物料装卸点位置进行了改进,讨论了布局中装料点与卸料点分离的情况,且其位置不限定在作业单元中心或中心线上,该思想比较符合实际。
物料搬运费用通常是设施布局设计中首要考虑的因素,因此设施布局模型中搬运距离的准确表示也将直接影响布局方案的优劣。目前诸多设施布局问题研究中,常用欧氏距离(直线距离)[5-6,9]和曼哈顿距离(矩形距离)[3-4,7-8,10-13]表示作业单元之间的物料搬运距离,然而实际物料搬运中,搬运设备通常沿着避开障碍的通道进行物料搬运,因此采用欧氏距离和曼哈顿距离这两种简化的搬运距离计算方法可能会引起较大误差,使最终布局方案不能满足设计要求[14]。为了使搬运距离的计算更加符合实际,黄小荣[15]以多行设施布局问题为研究对象,提出一种实际搬运距离计算方法,然而文中布局方案没有设计搬运通道,且未考虑物料装卸点实际位置对搬运距离计算的影响;lee等[16-17]采用预先构建的邻接图将搬运设备的行进路线限定在通道上,进而采用Dijkstra算法求出物料搬运的最短距离,然而所有通道的位置均假设为固定,且未考虑物料装卸点的实际位置。
为解决以上问题,本文以多行设施布局问题为研究对象,提出考虑物料装卸点与搬运通道的多行设施布局设计方法;对多行设施布局问题中的物料装卸点表示方法进行分析,并在考虑物料装卸点的前提下,分析多行设施布局中搬运设备沿搬运通道进行物料搬运的距离计算方法,其中着重分析与构建避障搬运的最短路径表示方法和求解算法;建立更加符合实际的多行设施布局优化模型,并设计遗传模拟退火(Genetic Simulated Annealing, GSA)算法对模型进行求解,以对GA和SA两种算法取长补短,生成更加有效且切合实际的布局方案。
1 问题描述和分析
1.1 问题描述
考虑物料装卸点和搬运通道的多行设施布局可以描述为:将若干个作业单元分配到多个具有相同高度的固定行中,装料点和卸料点通常位于作业单元内的边缘位置,搬运设备沿搬运通道行进,目的是使设计目标集达到最大或最小化。同时,问题还有以下假设条件:
(1)作业单元内的装料点和卸料点通常位于作业单元内部的边缘,并靠近同一横向通道的位置,有特殊作业单元(如原料存放区)的物料装卸点在其中心位置。
(2)给定作业单元内物料装卸点的初始位置,但可以根据特定规则发生一定改变。
(3)布局总区域的面积大于所有作业单元与通道所占面积之和。
(4)横向通道与纵向通道的数量、宽度均为已知,横向通道的位置已定,纵向通道位于中间行内,每一中间行内纵向通道的数量已知,但其位置不定。
(5)布局总区域与作业单元的形状均为矩形,长宽为固定值,作业单元的宽度与行的宽度相等。
图1所示为考虑物料装卸点与搬运通道的多行设施布局形式,wf为行或作业单元的宽度,wh和wv为横向通道与纵向通道的宽度。
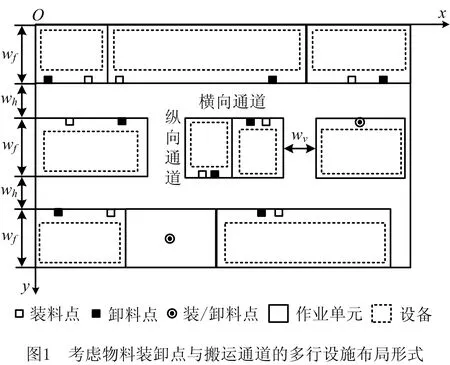
1.2 物料装卸点位置的定义与分析
考虑物料装卸点位置的情况下需要进一步考虑作业单元的方向,即作业单元的摆放形式。本文定义了多行设施布局中作业单元的4种摆放形式,如图2所示。其中:图2a为给定原始作业单元i的中心位于笛卡尔坐标系的原点,装料点坐标为(xO,yO),卸料点坐标为(xI,yI);图2b为原始作业单元内的设备与物料装卸点同时绕作业单元中心旋转180°后所呈现的摆放形式;图2c为原始作业单元中的设备倒置或倒序排列后所呈现的摆放形式,物料装卸点会以y轴为对称轴发生类似于镜像的位置变化;图2d为原始作业单元同时旋转与镜像后所呈现的摆放形式。
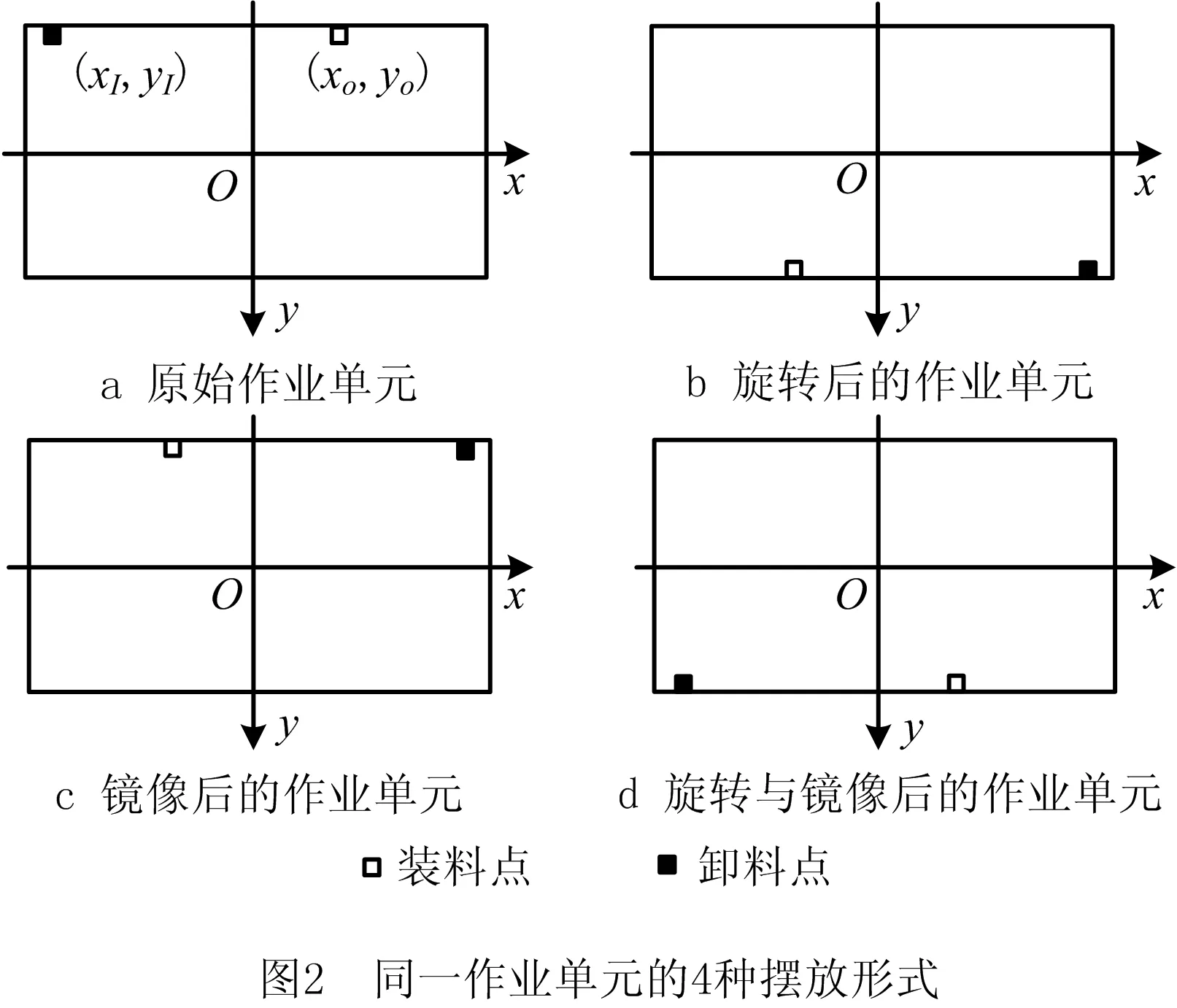
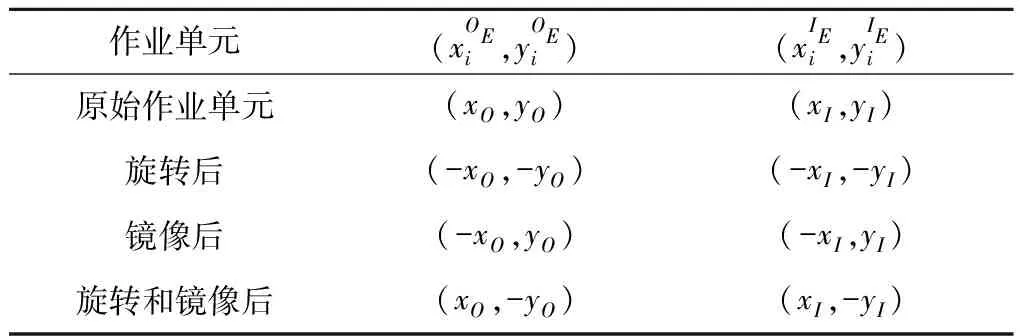
表1 物料装卸点在作业单元中的表示
以上定义了物料装卸点位置在局部作业单元内的表示方法,作业单元的中心位置定义为坐标原点。然而在布局整体坐标系中,作业单元的中心位置为其实际中心位置,因此需要将作业单元内的物料装卸点坐标转化为布局整体坐标系中的坐标。对于图2中的4种情况,物料装卸点坐标从局部作业单元转化至布局整体坐标系的过程均可表示为:
(1)

1.3 物料搬运精确距离分析
为了避免欧氏距离和曼哈顿距离表示物料搬运距离时的缺点,提出多行设施布局中搬运设备沿通道进行物料搬运的精确距离计算方法。为了便于分析,本文将多行设施布局中的物料搬运分为无障碍搬运和避障搬运。
1.3.1 无障碍搬运
无障碍搬运描述为:为完成一次物料搬运,搬运设备除了装卸物料时需要转变行进方向以进入作业单元内部外,其余时刻只沿一条横向通道直线行进,其基本类型如图3所示。
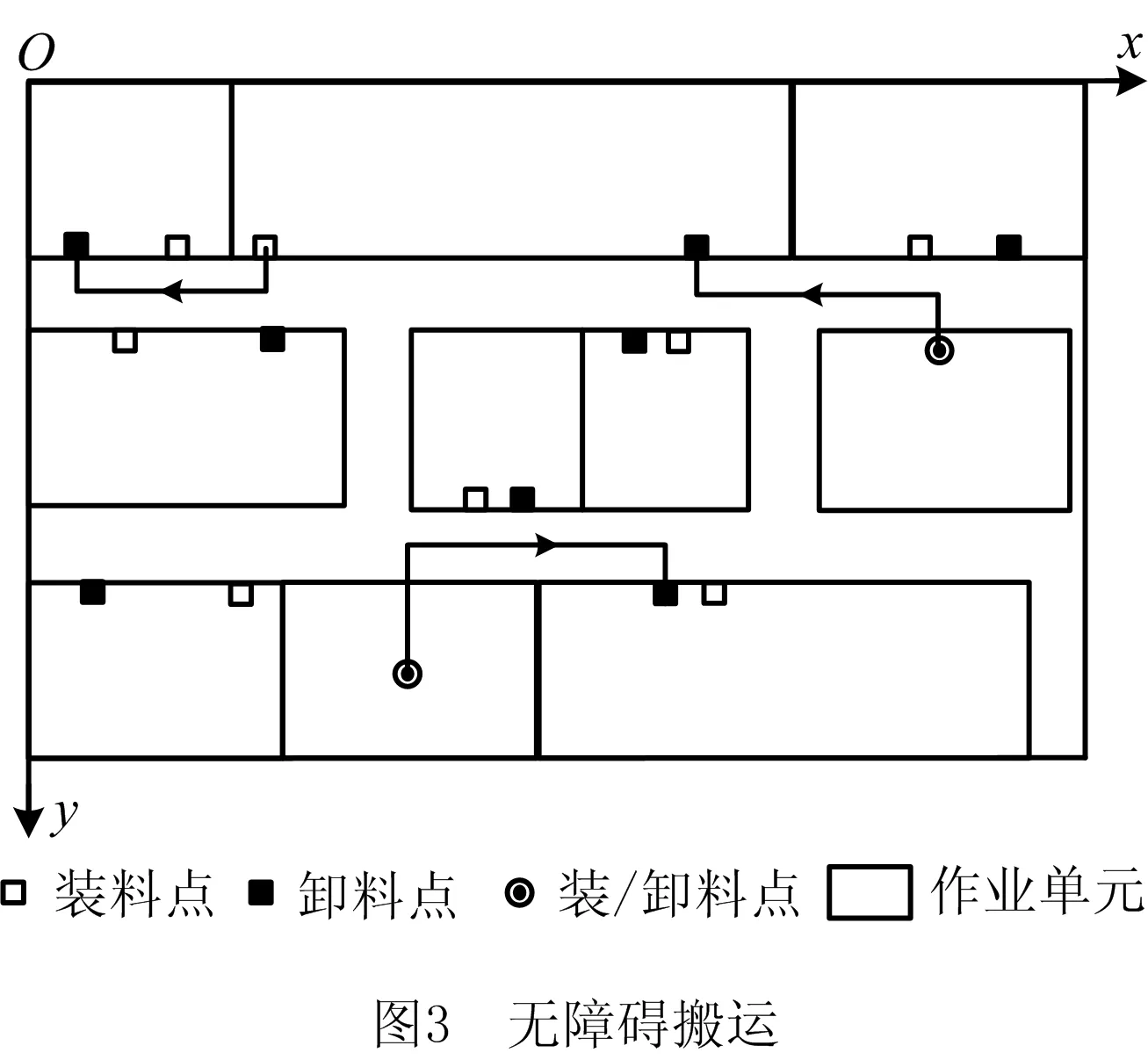
图3中的无障碍搬运距离
diOjI=
(2)
式中:diOjI为作业单元i的装料点到作业单元j的卸料点的实际搬运距离;y′为作业单元i的装料点和j的卸料点临近的同一横向通道y方向上的中心坐标。
1.3.2 避障搬运及其表示方法
避障搬运描述为:为完成一次物料搬运,搬运设备除了装卸物料时需要转变行进方向外,还会因需要沿避开作业单元阻挡的纵向通道行进而转变方向,即搬运过程中会穿过某些行。避障搬运中,通常要经过两条或两条以上横向通道,且会经过纵向通道,其基本类型如图4所示。
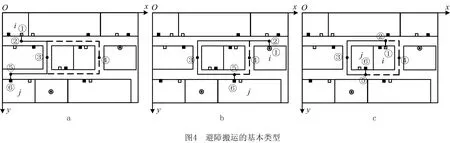

节点个数和坐标确定后,需要确定如图5所示的邻接图和邻接矩阵,邻接图中每条有向边的长度表示相连两节点之间的曼哈顿距离,而不可达节点之间的距离为∞,可见图5中①~⑥有两条可以选择的路径。需要注意的是,若中间行的数量或中间行内纵向通道的数量增加,则物料搬运可供选择的路径将会增加,如图6所示。


1.3.3 避障搬运距离计算的Dijkstra算法
Dijkstra算法是一种基于图论的算法,适用于计算单源点最短路径问题。设G={V,E}为一类似于图5和图6中构建的带权有向图,EN×N类似于图5中的邻接矩阵,V={V1,V2,…,VN}为节点集合,节点集合分为S和U,S中的节点已经计算出源点至其最短路径,U中的节点未计算出源点至其最短路径。设VO为装料点(源点),用d[i]记录当前已知的VO至Vi的最短距离,则Dijkstra算法计算物料搬运避障最短距离的步骤如下:
(1)初始化S={VO}与U中各节点的d[i]值,若VO至Vi可达,则d[i]为VO至Vi的曼哈顿距离,否则d[i]=∞。
(2)从U中选择d[i]值最小的节点Vk加入S。
(3)以Vk作为新的中间点,更新U中各节点的d[i]值,更新方式为d[i]=min{d[i],d[k]+Eki}。
(4)重复(2)和(3),直到U中无节点。
上述步骤执行完之后,即可求得装料点到卸料点的避障最短搬运距离,即实际搬运距离。
2 数学模型
2.1 物料搬运成本
物料搬运成本为作业单元间物流量与实际搬运距离乘积的总和,其目标函数表示为
(3)
式中:n为作业单元的数量;fiOjI为作业单元i的装料点至作业单元j的卸料点的单向物流量;diOjI为作业单元i的装料点至作业单元j的卸料点的实际搬运距离,计算方法见1.3节。
2.2 搬运设备空载运行成本
搬运设备空载运行以图7说明。搬运设备搬运作业单元k至l之间物料的同时,作业单元i的物料需要运送至作业单元j,搬运设备则将正在搬运的物料送至作业单元l后,由作业单元l处的卸料点空载运行至作业单元i的装料点处,才能完成作业单元i至j的物料搬运请求。

搬运设备执行下一项物料搬运任务前处于不确定的作业单元卸料点处,用Pl表示其处于作业单元l的卸料点处的概率,
(4)
由式(4)可知,如果其他作业单元至作业单元l有较大的物流量,则搬运设备处于作业单元l的卸料点处的概率较大,反之则较小。搬运设备为完成作业单元i至作业单元i的物料搬运所需空载运行的距离为
(5)
进一步,搬运设备空载运行成本的目标函数可以表示为
(6)
式中c为搬运设备的空载系数。
2.3 相互关系
与物料搬运不同的是,作业单元之间的相互关系是一种功能性关系,其目标函数中,使用作业单元中心点之间的曼哈顿距离进行计算。目标函数可以表示为:
(7)


表2 相互关系等级的量化取值
2.4 约束分析
多行设施布局在寻求目标集最优化的同时,还要满足作业单元不重叠、不越出布局区域边界、物料装卸点靠近横向通道等约束。为了便于描述与理解,首先定义以下变量:
(8)
(9)
(10)
(11)

(12)
进一步,考虑物料装卸点与搬运通道的多行设施布局约束条件如下:
(13)
(14)
(15)
(16)
αi1βi=1,i∈[1,n];
(17)
αimβi=0,i∈[1,n];
(18)
i,j∈[1,n],i≠j;
(19)
i∈[1,n],l∈[1,nt];
(20)
i,j∈[1,n],i≠j;
(21)
i∈[1,n],l∈[1,nt];
(22)
l,u∈[1,nt],l≠u;
(23)
(24)
(25)
βi,ηi=0,1,i∈[1,n];
(26)
αik=0,1,i∈[1,n],k∈[1,m];
(27)
δlk=0,1,l∈[1,nt],k∈[2,m-1]。
(28)

式(13)和式(14)保证一个作业单元只能属于一行;式(15)和式(16)保证一个纵向通道只能属于一个中间行内;式(17)和式(18)保证第一行与最后一行中作业单元内的物料装卸点靠近横向通道;式(19)保证任意两个作业单元不重叠,式(20)保证任意一个作业单元与任意一个纵向通道不重叠;式(21)~式(23)为布局中的边界约束;式(24)保证任意两个纵向通道不相邻排列;式(25)为纵向通道的位置约束;式(26)保证任意一个作业单元有4种可能的摆放形式;式(27)和式(28)为决策变量的取值范围。
3 求解算法设计
3.1 遗传算法与模拟退火算法的结合
本文所提多行设施布局问题是一种多目标离散优化问题,该布局问题的求解不仅与作业单元之间的相对位置排列有关,还受作业单元自身摆放形式、纵向通道位置等影响,求解难度更大。为能较好地解决本文所提问题,提出一种采用分段编码方式表示布局方案信息的GSA算法。
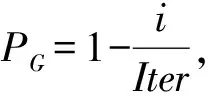
3.2 适应度函数的构建
由于式(3)、式(6)和式(7)中diOjI与rij的度量单位不同,如果将这3种目标函数直接结合,则可能引起较大误差。因此在构建适应度函数之前,首先对其分别进行标准化处理,物流量与相互关系等级标准化处理的过程如式(29)和式(30)所示。
(29)
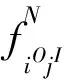
(30)

引入权重系数w1,w2,w3与常数C,构建适应度函数
(31)
式中:F恒大于0;0 本文采用GA编码的思想,以染色体表示布局方案。将染色体分为4段,如图8所示。 图中染色体表示作业单元数量为n、纵向通道数量为nt的多行设施布局。其中:第1段表示作业单元的排列顺序,ui为作业单元的代号,本文规定作业单元的排列顺序为自上向下、自左向右,遵守自动换行策略;第2段表示作业单元是否发生旋转,其上的基因与第1段的基因相对应,si=0时原始作业单元不发生旋转,si=1时原始作业单元旋转;第3段表示作业单元是否发生镜像,同样其上的基因分别与第1段的基因相对应,mi=0时原始作业单元不发生镜像,mi=1时原始作业单元镜像;第4段表示纵向通道在指定行中的位置,vi为整数,取值范围与其对应行中作业单元的个数有关。 本文采用顺序交叉方式,针对染色体前3段进行交叉,交叉步骤为:首先从父代P1的第1段染色体片段中随机选择连续的一组位置,将这些位置对应的基因复制到一个空染色体的相应位置上,构成一个原始后代;删去父代P2第1段上相应的基因,将P2第1段上剩余的基因按顺序填入原始后代第1段染色体片段的空缺位置上;染色体第2段与第3段基因随第1段也发生相应交叉,父代P1的第4段基因直接复制到原始后代中,形成子代C1,并以同样的方式产生另一个子代C2。顺序交叉方式如图9所示。 (1)基因位置的互换变异 基因位置的变异采用互换变异的方法,随机选择染色体第1片段上的两个位置,将这两个位置上的基因互换,相应第2段和第3段染色体片段上基因的位置也进行互换,如图10所示。 (2)旋转、镜像与通道变异 旋转变异、镜像变异和通道变异分别针对第2~4段染色体片段进行变异,变异过程如图11所示。 以上3种变异中,通道变异是染色体未发生交叉和互换变异时才会进行的一项变异操作,目的是在作业单元相互位置不改变时,通过改变纵向通道位置进行局部寻优。例如染色体第4段上的一个基因由1变为3,则纵向通道位置由该行第1个作业单元的右侧,变为该行第3个作业单元的右侧,其变异表达方式如图12所示。 (1)边界修正 本文规定作业单元的排列为自上向下、自左向右的顺序,遵守自动换行策略,因此最下方一行作业单元可能会越出右侧边界,如图13所示。 (2)方向修正 图14中边界约束修正完成后,即可产生纵向通道的位置,如图15所示。因为大部分作业单元内的物料装卸点要求位于靠近横向通道的位置,所以修正了边界约束后,还要对作业单元的方向进行修正。以图14为例,方向修正后的染色体及布局如图15所示。 SA操作每产生一个新的解,都会与当前解进行对比,该操作可能接受比当前解更差的解。设ΔE为新解与当前解的适应度值之差,则对于求最大值的优化问题,新解被接受的概率 (32) 式中:k为Boltzmann常数;T为当前温度。 本文SA操作采用3.5节的变异方式产生新解。设Rand为取自区间[0,1)上服从均匀分布的随机浮点数,若Rand∈[0,0.25),则随机发生一次基因位置的互换变异;若Rand∈[0.25,0.5),则随机发生一次旋转变异;Rand∈[0.5,0.75),则随机发生一次镜像变异;若Rand∈[0.75,1),则随机发生一次通道变异。 本文将GA与SA结合,旨在使两种算法取长补短,提高算法求解设施布局问题的寻优能力和稳定性。本文GSA算法的步骤如下: 步骤1初始化染色体种群中个体的前3段。 步骤2修正边界,产生染色体的第4段(即随机产生纵向通道的位置),然后修正方向。 步骤3计算适应度,并检验是否达到最大迭代次数,若满足则输出最优解,否则执行步骤4。 步骤4更新迭代次数i和当前火温T,火温更新大小由退火因子r决定,采用精英保留策略与轮盘赌方法选出下一代染色体。 步骤6检验是否达到最大迭代次数,若满足则输出最优解,否则转步骤4。 图16所示为本文所提GSA算法的流程。 某矩形车间长76 m,宽30 m,车间内有15个作业单元,拟布置在3行内。横向通道、纵向通道的宽度均为3 m,行与作业单元的宽度均为8 m,其中中间一行要求有两条纵向通道。作业单元的长度与局部作业单元内物料装卸点的坐标信息如表3所示。 表3 作业单元信息 作业单元间的物流量矩阵D与相互关系矩阵R分别为: 适应度函数中,常数C=25,空载系数c与搬运设备类型相关,本文取为0.6,权重系数w1,w2,w3由专家打分法得出,分别取为0.4,0.3,0.3,根据原始数据可求得dmax=94.5 m。 针对上述案例,分别采用GA,SA,GSA求解,并将改进烟花算法(Improved Fireworks Algorithm, IFA)[19]、布谷鸟搜索(Cuckoo Search, CS)算法[20]与两阶段改进模拟退火(Improved Simulated Annealing, ISA)算法[21]应用于本文案例进行对比分析。6种算法的迭代终止规则均由迭代终止次数Iter控制,Iter=500。GA的种群规模Pop_size=50,交叉概率Pc=0.9,互换变异概率Pe=0.1,旋转变异概率Ps=0.1,镜像变异概率Pm=0.05,通道变异概率Pv=0.1;SA算法中为单个体寻优,初始火温T=2 000,扰动次数Sn=200,退火因子r=0.96,Boltzmann常数k=1;GSA算法中种群规模Pop_size=50,交叉概率Pc=0.9,互换变异概率Pe=0.1,旋转变异概率Ps=0.1,镜像变异概率Pm=0.05,通道变异概率Pv=0.1,初始火温T=2 000,扰动次数Sn=200,退火因子r=0.96,Boltzmann常数k=1;IFA中种群规模Pop_size=50,搜索深度系数αd=5;CS算法中种群规模Pop_size=50,抛弃概率pab=0.25,步长缩放因子αs=0.02;ISA算法中为单个体寻优,初始温度T=100,退火因子r=0.98,Boltzmann常数k=1,最小抽样次数Mstep=5,抽样阈值Rin=8,退火阈值Rout=20,终止温度Tend=1。 采用C++语言分别编写以上6种算法的程序,每种算法分别进行20次独立测试。6种算法得到的最优适应度为39.133 6,对应的最优染色体及最优染色体解码后的布局如图17所示。 表4所示为6种算法分别独立测试20次得到的最优适应度数据,可以看出相比其他5种算法,GSA算法搜索到的解的质量与稳定性具有比较明显的优势。 表4 不同算法最优适应度的对比 图18所示为6种算法分别独立测试20次的平均最优适应度进化曲线。从6种算法搜索到的解的质量来看,GA,CS,ISA较差,原因可能是GA,CS两种算法的局部搜索能力较差,ISA算法为单个体寻优,多样性差,而且采用的2-opt算子在本案例搜索中不具优势,搜索深度不够。而SA,GSA,IFA搜索到的解的质量较高,SA算法相对较好的搜索质量在一定程度上表明本文SA操作的可行性,但由于缺乏跳出局部最优的算子,导致其在进化中后期难以搜索到更好的解;IFA在进化初期就进行了局部深度搜索,因此表现出了较好的性能,但进化中后期搜索速度较慢,原因可能是IFA所采用的两点变异操作不能较好地跳出局部最优;GSA算法在进化初期主要进行遗传操作,该时期GSA算法不具优势,但在进化中期,随着SA操作执行次数的增加与火温T的降低,其搜索到的解的质量很高,逐渐超过CS,ISA,IFA,并在进化后期一定程度上克服了SA的缺点,平均最优适应度进化曲线仍然有上升的趋势,原因是GSA算法由多个个体寻优,且进化后期少量的交叉、变异操作有利于算法扩大搜索空间,跳出局部最优并使搜索进一步趋于全局最优,因此GSA算法较好地融合了GA和SA的优点,求解本文案例的效果较好。 本文针对多行设施布局尤其是两行以上的布局问题,提出考虑物料装卸点与搬运通道的多行设施布局设计方法,具体如下: (1)分析了物料装卸点位置在作业单元内的表示方法,及其从作业单元内向布局整体坐标系转化的方法,使布局问题更加切合实际。 (2)分析了多行设施布局中搬运设备沿通道进行物料搬运的精确距离计算方法,重点构建了避障搬运的邻接图和邻接矩阵表示法,并设计了基于邻接图和邻接矩阵的避障搬运距离Dijkstra算法,可为复杂系统中的物料搬运系统设计提供参考。 (3)构建了以物料搬运成本、搬运设备空载运行成本和作业单元间相互关系为目标函数的布局优化模型,分析了考虑物料装卸点与搬运通道的多行设施布局约束条件,并设计了求解模型的GSA。以一个三行设施布局为实例,采用所提算法生成了切合实际的布局方案,证明了所提算法在寻优能力和稳定性方面均具有较好的性能。 未来将进一步研究具有不规则作业单元形状的设施布局问题,以丰富该领域的模型和设计方法。另外,还需要深入研究多行设施布局形式以外的其他设施布局问题,并针对物料搬运通道或路线进行重点分析和设计。3.3 编码方式

3.4 交叉操作

3.5 变异操作



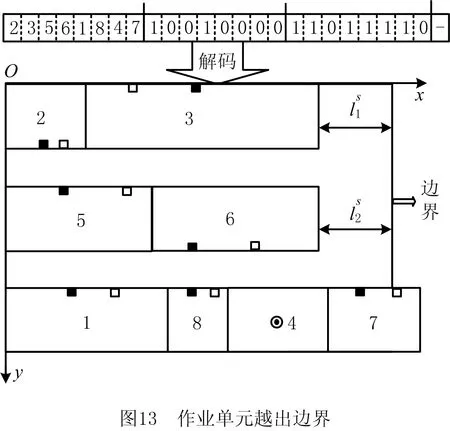
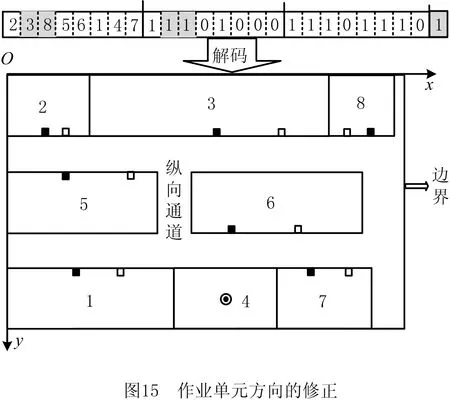
3.6 修正操作


3.7 模拟退火操作
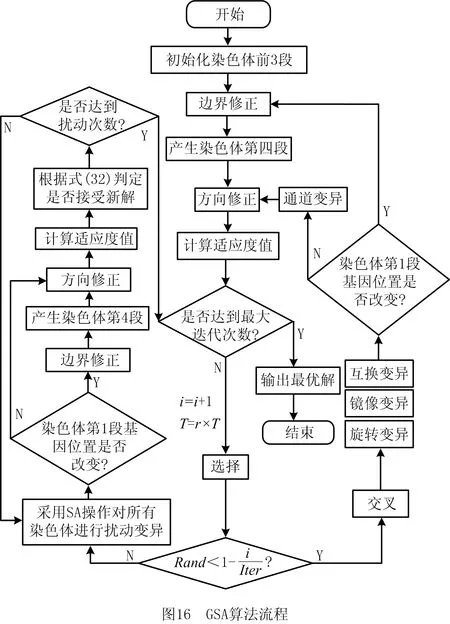
3.8 遗传模拟退火算法流程
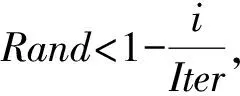
4 案例分析
4.1 原始数据
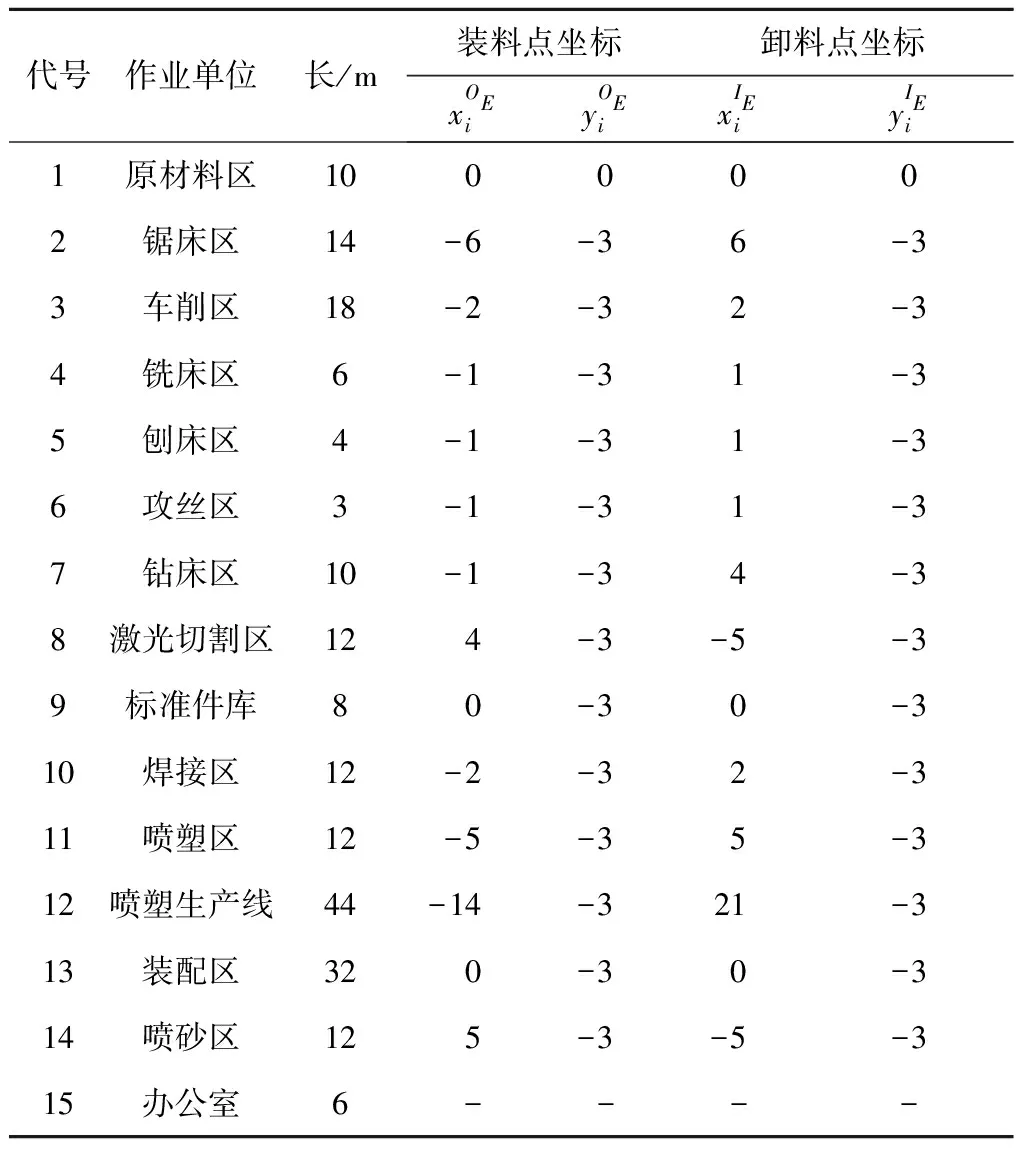


4.2 实例求解

4.3 算法分析
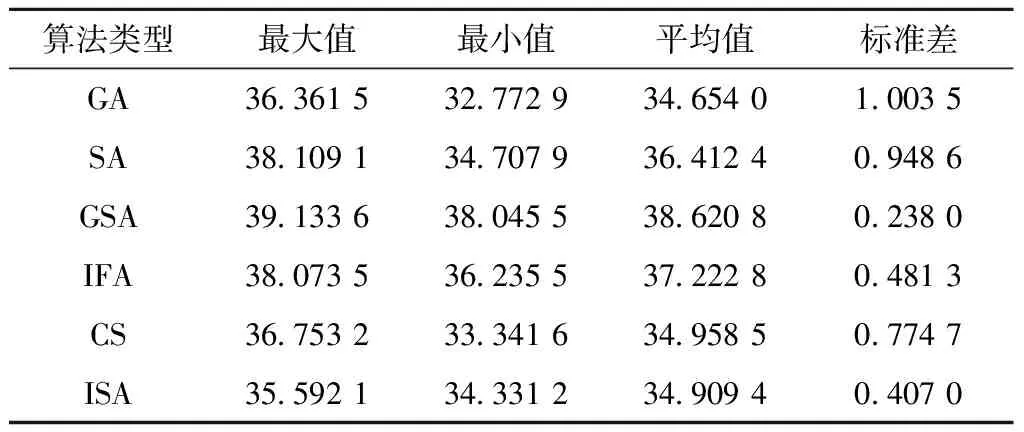
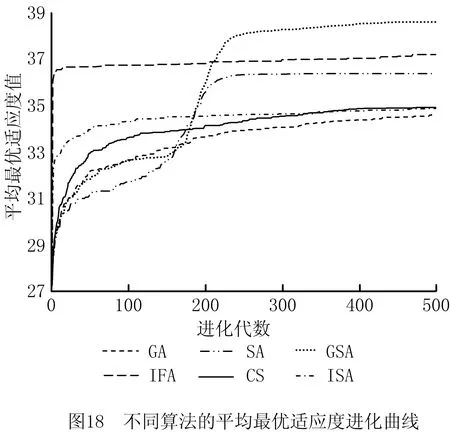
5 结束语

