鞋楦五轴数控加工中的刀具半径补偿算法

王 恒，王云鹏,武彦伟，程卫东

(北京交通大学 机械与电子控制工程学院，北京 100044)

0 引言

我国是制鞋大国，鞋楦是鞋的成型模具，其加工质量影响到鞋的尺寸精度，因此鞋楦加工成为制鞋中的关键技术。五轴联动数控机床是一类专门用于加工复杂曲面的高精密机床[1]，目前已经可以采用五轴数控加工鞋楦。

五轴数控加工中的刀具磨损会降低鞋楦的加工精度，更换刀具又会提高生产成本，有必要对刀具半径进行补偿，而确定半径补偿方向是其中的关键[2]。鞋楦数控加工方式为端铣加工，其理想的刀具半径补偿方向为切触点法向量。

若数控程序能够输出切触点坐标，则可通过刀心点坐标和刀具尺寸计算得到切触点法向量。文献[3-8]分析了球头刀、环形刀和平底刀的刀具半径补偿原理，利用程序提供的切触点坐标和刀心点坐标推导出切触点法向量，得到半径补偿公式。以上对切触点法向量的推导均需数控程序输出切触点坐标，然而现在很多数控程序并不提供切触点信息，限制了以上方法的适用范围。

数控程序未提供切触点坐标时，中国科学院数学与系统科学研究院的韩丽提出一种将刀心点法向量作为刀具半径补偿方向的补偿方法；Han等[9]以NC代码为输入，运用形状重构技术进行刀位表面重构，求出刀位点的表面法向量，通过推导刀位点法向量与切触点法向量之间的关系得到对应的切触点法向量，并在球头刀和平底刀上得到了验证；文献[10]针对应用截平面法生成的刀具路径，利用刀心点及其邻域点拟合平面得到刀心点法向量，并将法向量统一调整为指向工件外侧，以刀心点法向量作为该点刀具半径补偿的方向。鞋楦加工数控程序未提供切触点坐标，这种将刀心点法向量作为补偿方向的补偿方法为解决切触点缺失时刀具半径补偿方向的确定问题提供了很好的思路。

利用计算量较少的拟合平面求得曲面法向量，法向量调整是关键。孙金虎等[11]对薄壁特征、垂直法相和相邻曲面3种情况分别进行处理，以更快更准确地调整法向量；何华等[12]减小了调整法向量的搜索范围，并增加了搜索时的法向量传播个数，以提高法向量调整的效率，并用约束法向量传播方向的方式提高准确性；吴良武等[13]改进了邻域加权平均法，只在相关边界体素间进行光顺操作，使生成的物体表面更加细腻。

本文以鞋楦五轴数控加工为对象，针对相邻刀心点法向量可能出现偏差较大的情况，提出一种全局刀心点法向量的光顺方法，使得在算法复杂度小的情况下仍能实现法向量光顺。然后将光顺后的刀心点法向量作为刀具半径补偿方向，对这种刀具半径补偿算法进行了仿真验证。

1 圆环面刀具半径补偿原理

1.1 圆环面刀具

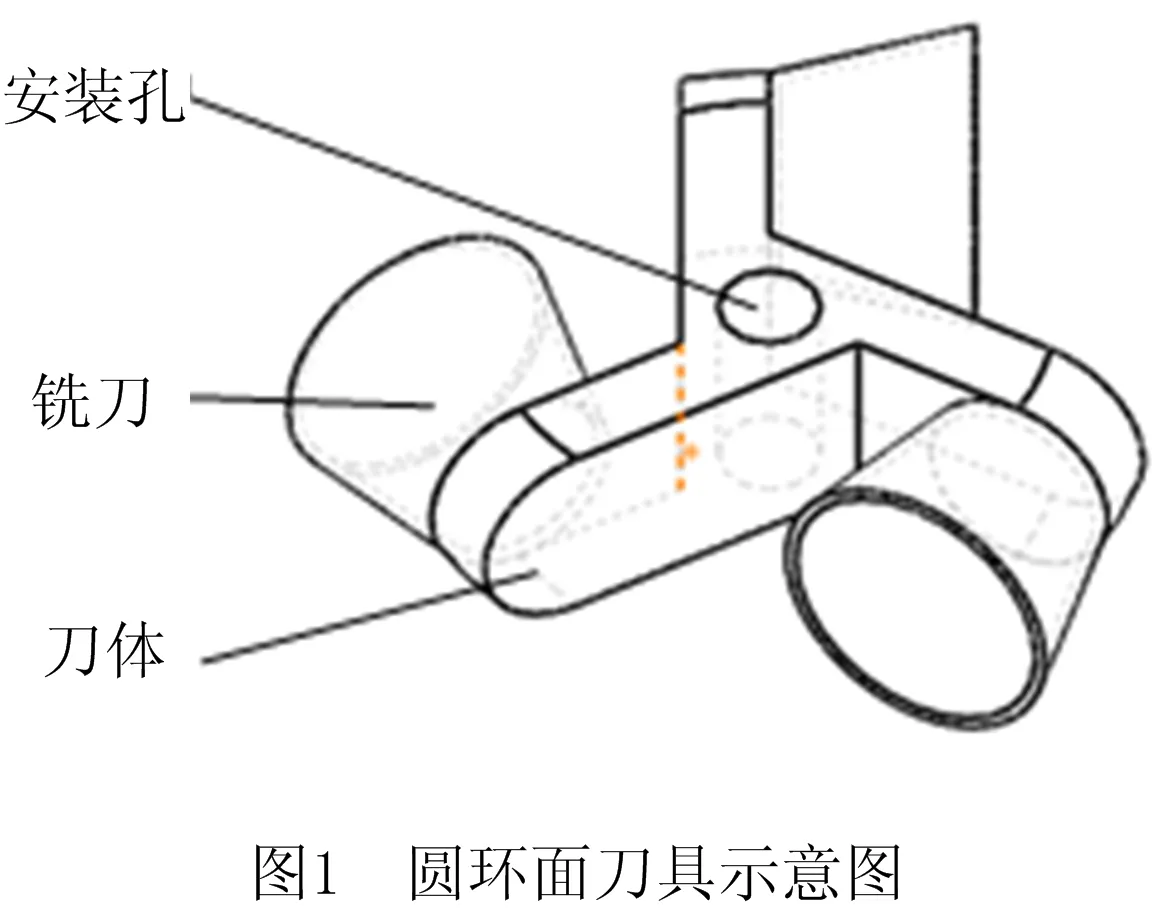
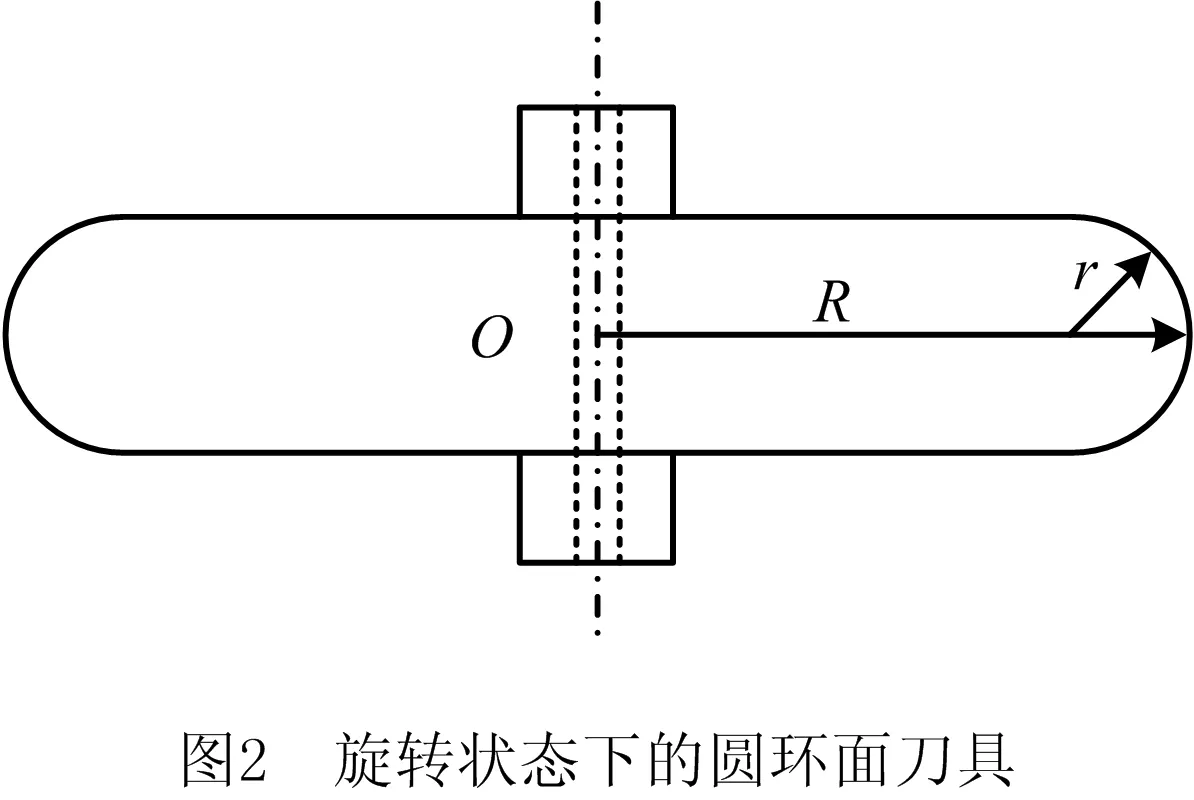
鞋楦加工所用的刀具为圆环面刀具，如图1所示，本文以圆环面刀具为例对刀具半径补偿进行问题描述。圆环面刀具由3个均匀分布的切削刃构成，通过安装孔装在主轴上，旋转状态下呈圆环状，如图2所示。图中，R为刀具大径，r为刀具小径，O为刀心点，轨迹规划生成的刀位轨迹即为刀心点的位置轨迹。

1.2 刀具半径补偿原理

使用五轴数控机床加工鞋楦时，刀具与工件为点接触，刀具未磨损时，其与工件的切触位置为轨迹规划得到的理论切触点；当磨损导致刀具半径减小时，如果仍按原数控程序走刀，则刀具和工件的切触位置相对于理论切触点偏工件外侧，将造成工件欠切。

鞋楦加工过程中涉及的5个运动轴为X，Y，Z，B，C。其中：X，Y，Z为平动轴的运动坐标；旋转轴B决定刀轴摆角，该角度在轨迹规划时事先由经验确定；旋转轴C决定工件的旋转角度，为了使切削速度均匀，转轴C匀速变化。在刀补时，维持B，C两轴坐标值与轨迹规划时相同，仅改变X，Y，Z的数值，即通过在空间内平移刀心点进行刀具半径补偿，这样既减小了五轴数控刀补的复杂程度，又有别于三轴数控刀补中的平面补偿，以下描述刀具半径补偿算法时不再涉及B，C两旋转轴。鞋楦加工的刀具半径补偿原理如图3所示。

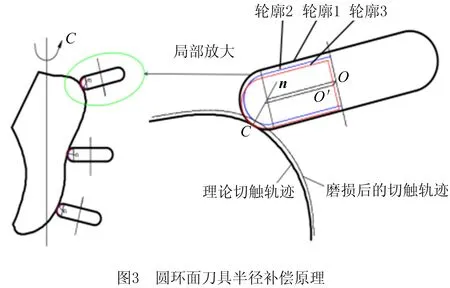
图3局部放大部分的C点为当前切触点，n为当前切触点的法向量。刀具轮廓1为磨损前刀具位置，刀具轮廓2为磨损后未进行刀具半径补偿时的刀具位置，刀心点均为O。刀具磨损后，刀具和工件切触位置偏离理论切触点C。刀具轮廓3为将磨损后的刀具沿切触点内法向量方向平移半径补偿值后的刀具位置，此时刀心点为O′，由刀具磨损产生的误差得到补偿。

2 刀心点法向量作为补偿方向的补偿方法

2.1 刀心点法向量作为补偿方向的使用条件

本文对螺旋线导动法生成的鞋楦加工轨迹进行研究。作为刀具半径补偿方向的补偿方式，刀心点法向量可以应用于螺旋线导动法生成的鞋楦加工轨迹，该刀位轨迹如图4所示。刀心点轨迹具有以下特点：

(1)文献[14]指出，两个一阶连续可微曲面作空间点接触的连续啮合运动时，两个曲面上的接触轨迹是连续的，并给出了该命题的证明。对于数控加工，两个连续可微平面一个是工件曲面，一个是刀具旋转形成的包络面。

(2)鞋楦五轴数控加工中，刀位轨迹采用螺旋线导动法生成[15]。Z轴以极小且较均匀的速度缓慢抬升，相邻刀心点间的刀轴矢量变化极小，工件坐标系下刀心点包络而成的形状与工件形状具有一定的相似性。

(3)在连续约360个刀位点组成的环形轨迹上，Z坐标变化量主要取决于使用螺旋线导动法生成刀位轨迹时的螺旋线节距。为了提高加工精度，螺旋线节距取值很小，可认为这些刀位点近似处于一个平行于XOY的平面内。在加工过程中，随着刀具缓慢提升，工件被由下到上切削，刀具自下而上抬升与工件被自下而上切削具有对应性。

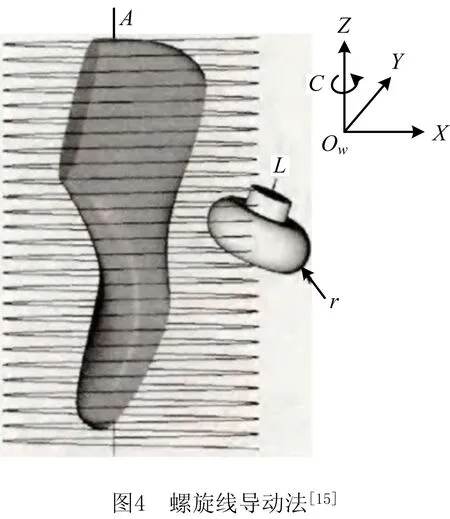
鉴于以上3个特点，将刀心点法向量作为刀具半径补偿方向成为一种可行的补偿方式。实际上，凡是用截平面法和螺旋线导动法生成的刀位轨迹均具有以上3个特点，因此可以采用刀心点法向量作为半径补偿方向的补偿方式。

2.2 刀心点法向量的求解

本文中刀心点法向量采用拟合平面的方式求解，即在由刀心点及其周围邻域内若干点组成的平面内近似求解刀心点法向量。一个平面有两个方向相反的法向量，采用拟合平面的方式求得的法向量方向难以预测，因此需对求得的刀心点法向量进行进一步调整，以使所有刀心点法向量具有统一的指向，具体步骤如下：

(1)拟合平面求刀心点法向量

工件坐标系下的刀位轨迹由大量独立点构成，单个点不存在法向量的概念，必须在面的概念下求法向量。为了尽可能让每个刀心点反映出工件的局部几何信息，在刀心点的邻域内选择k-1个与其距离最近的刀位点，这k-1个邻近点加上刀心点共k个点构成了当前局部曲面的组成要素。采用平面对所得的k个点进行拟合，将拟合平面的法向量作为所求的刀心点法向量。利用最小二乘法进行平面拟合，求当前k邻域的质心点

(1)

构造矩阵

(2)

求矩阵A的特征值和特征向量，A的最小特征值对应的特征向量即为所求点的法向量。为便于后续运算，所有法向量均转化为单位向量。

(2)法向量方向一致性的调整

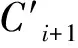
(3)

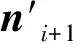
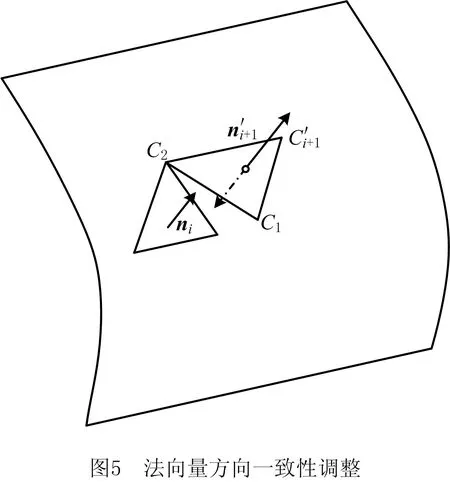
该调整方法需有初始参考向量，否则第一个刀心点法向量方向无调整依据。结合刀心点的包络形状和鞋楦底部形状，初始刀心点外法向量与Z轴近似平行，方向为Z轴负方向。因此设定初始参考向量为(0,0,-1)，以此为依据对初始刀心点法向量方向进行调整。

利用拟合平面求得的法向量本身存在偏差，经过法向量方向一致性调整后，可能出现相邻刀心点法向量方向偏差较大的情况。因此不仅要对所求得的法向量方向进行一致性调整，还要对偏差较大的法向量进行修正，以实现全局法向量的光滑过渡。

3 法向量光顺方法

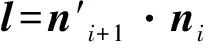
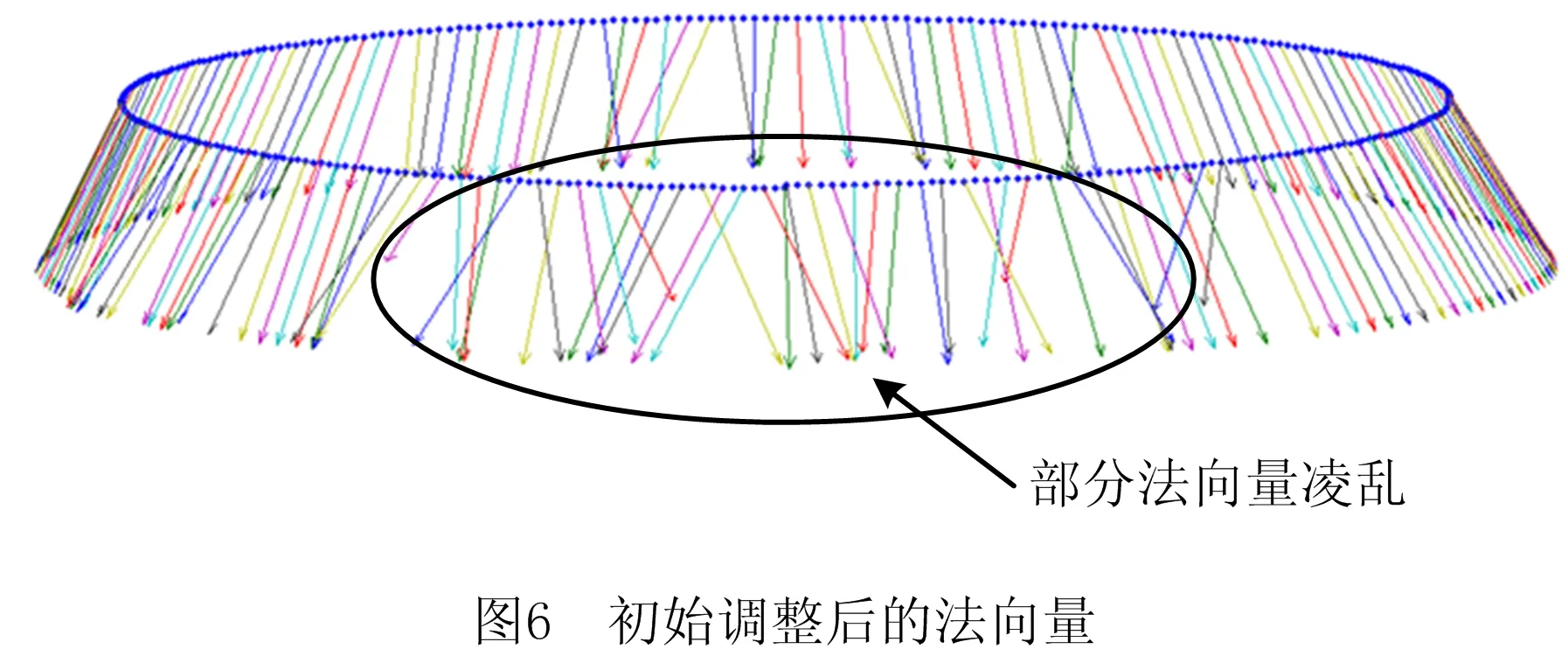
3.1 异常法向量的剔除

本文将异常法向量分为两种情况：①法向量在XOY平面内的投影不垂直于当前切平面；②法向量在Z方向的投影与附近刀心点法向量的偏差较大，找出异常法向量后对其进行置零。

(1)异常情况1

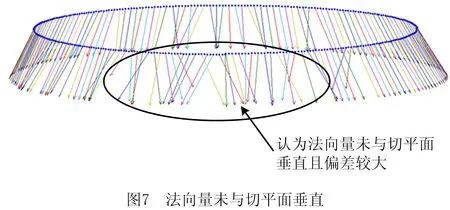
对图7中法向量在XOY平面内投影不垂直于当前切平面的情况进行处理。理论上某一点的法向量应和切平面垂直，即垂直于切平面内的任意一条直线。利用拟合平面的方式求法向量时，曲率较大处的刀位点信息可能会被其邻域点严重稀释，出现所求法向量与切平面不垂直的情形。当前刀位点的准确切平面未知，为了尽可能准确反映当前刀位点的切平面信息，将前一个刀心点和后一个刀心点之间的连线作为切平面内的一条直线，设前一个刀心点坐标为Pi-1(xi-1,yi-1,zi-1)，后一个刀心点坐标为Pi+1(xi+1,yi+1,zi+1)，则有

τ=Pi+1-Pi-1。

(4)

用τ表示当前刀心点Pi切平面内的一条直线，并转化为单位向量。设经过初步调整后刀心点Pi的法向量为ni，令

mult=|ni·τ|,

(5)

法向量与切平面垂直，理论上mult=0。设定mult的阈值为t，t为略大于0的正值，且根据需要进行相应修改。当mult>t时，将当前刀心点法向量置零，等待下一步处理。

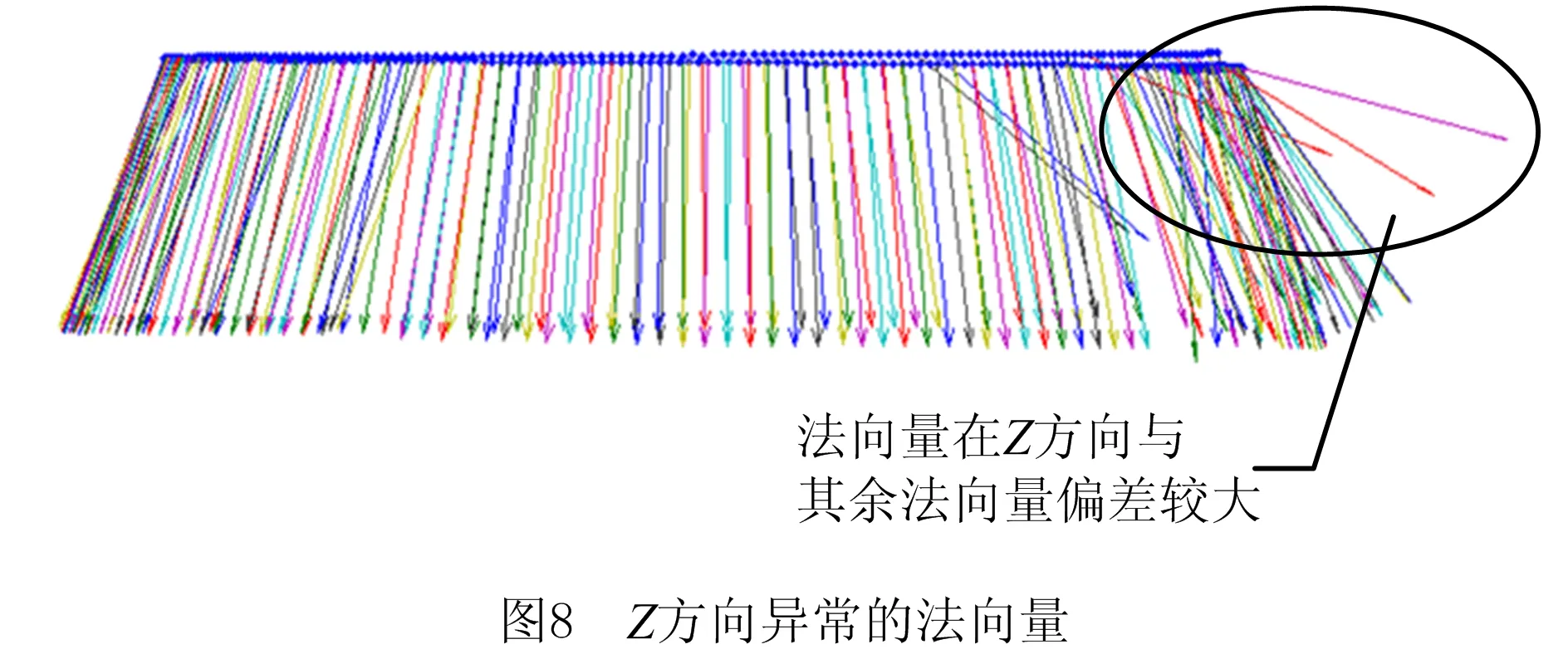
(2)异常情况2

对图8中法向量在Z方向的投影与附近刀心点法向量偏差较大的情况进行处理。约360个刀心点能够形成一个环形，以360个刀心点为一组进行逐次查找。求这360个刀心点法向量的平均值得到平均法向量

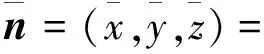
(6)

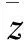
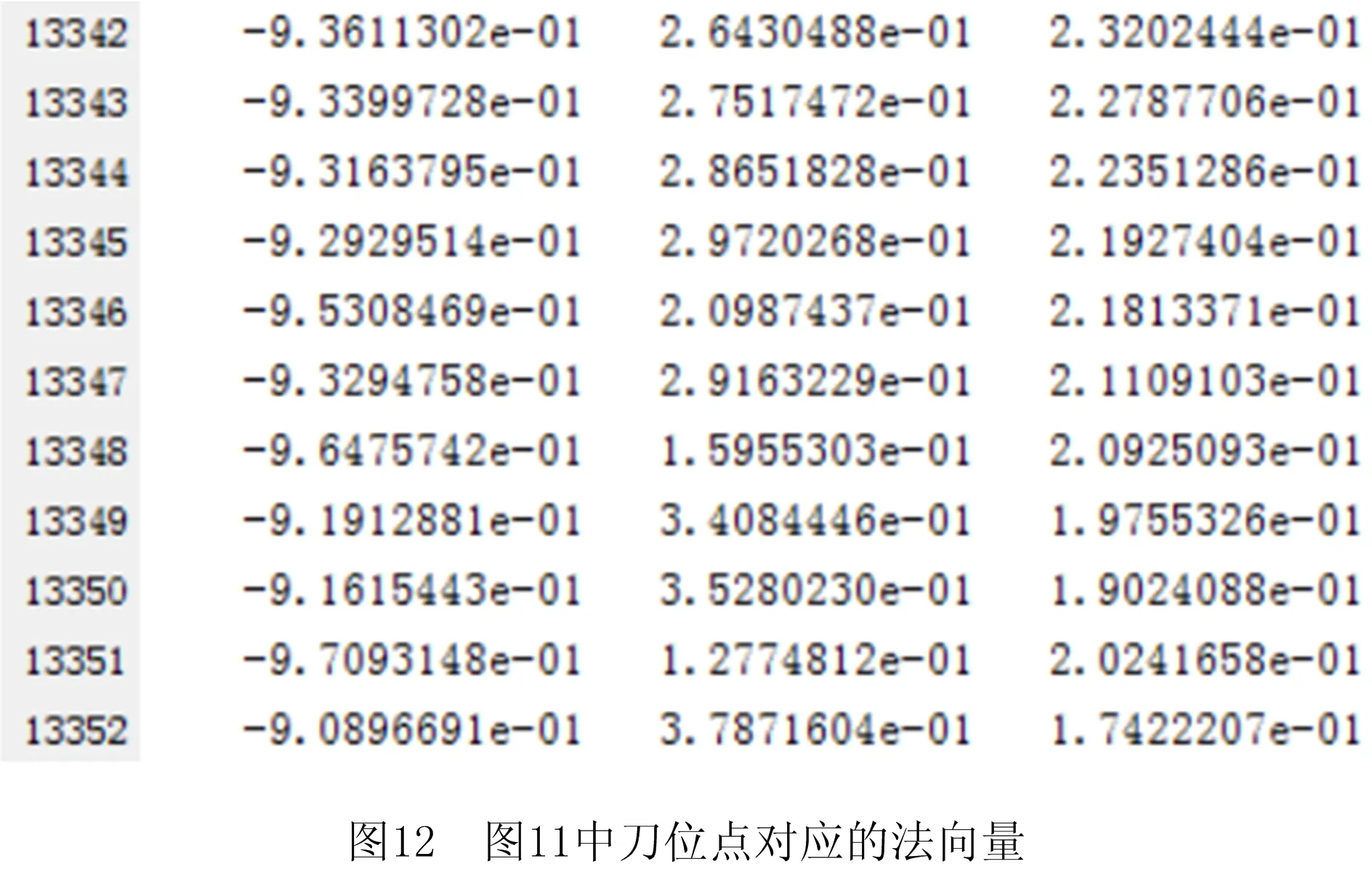
(7)

设定Δz的阈值q(0t时，将当前刀心点法向量置零，等待下一步处理。

3.2 异常法向量的修正

3.1节中对异常法向量进行了置零操作，下面对其进行修正。假设第i个刀心点法向量ni异常且被置零，首先逐个向前查找第一个不为零的法向量ni-j，j为当前刀心点与其向前第一个法向量不为零的刀心点的序号差；其次逐个向后查找其后第一个不为零的法向量ni+k，k为当前刀心点与其向后第一个法向量不为零的刀心点的序号差。对ni-j和ni+k间连续j+k-1个零向量进行线性插值得到修正后的法向量nic，

(8)

图6中的法向量经修正后得到的最终刀心点法向量如图9所示，图中相邻刀心点法向量偏差明显减小，基本实现了平滑过渡。以360个刀心点为一组逐次调整，最终得到的全局法向量如图10所示，所有法向量基本实现了平滑过渡。

3.3 补偿后刀心点的求解

3.2节中对异常法向量进行了修正，修正后的每个刀心点的法向量为nic，则对应的刀心点补偿向量nci=-nic，假设补偿量为Δr，则刀心点Pi经过补偿后的位置

(9)

求出经过补偿的刀心点位置后即可对数控程序进行处理。输入原数控程序，部分数控程序如图11所示。采用第3章的方法求对应刀心点的法向量，图11数控程序中刀位点对应的法向量如图12所示。法向量的反向量为对应刀心点的补偿方向，求得新的刀位点经运动学逆变换后得到的新的数控程序如图13所示。

4 仿真验证

为了验证算法的有效性，采用Vericut软件进行仿真。仿真条件为：原刀具尺寸大径为90 mm，小径为28 mm，实际磨损量为0.8 mm。

(1)法向量光顺前的仿真

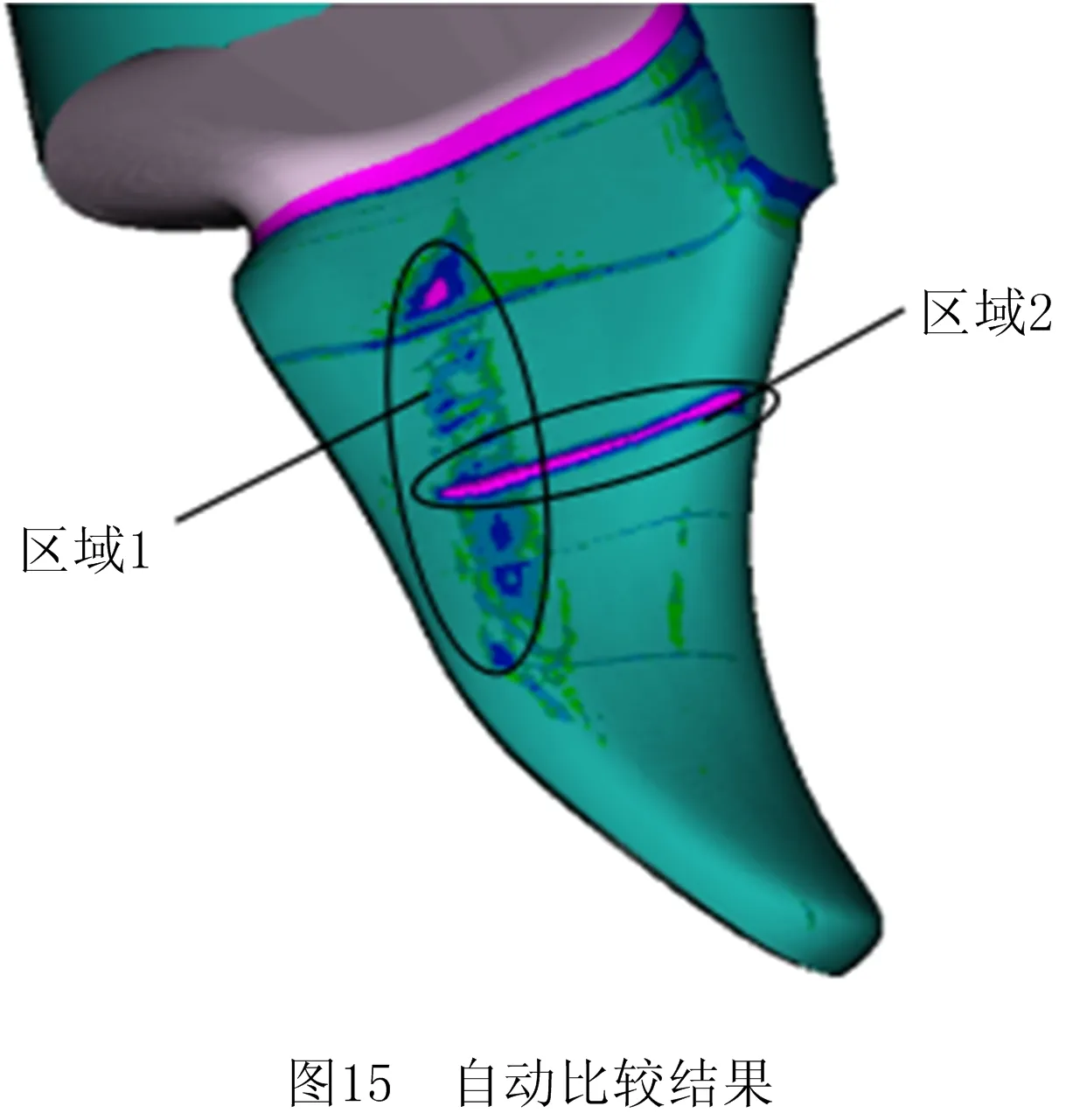
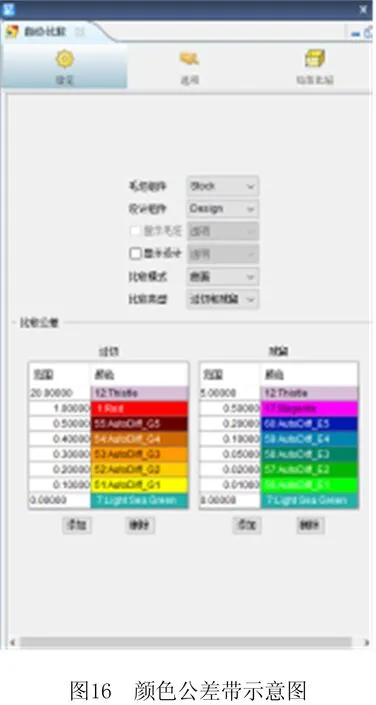
计算每个刀心点的法向量，并将其统一调整为指向包络面外侧，调整后的刀心点法向量作为对应刀心点刀具半径补偿的方向。对该补偿方法进行仿真，得到的仿真结果如图14所示。从图中可以看到，鞋楦中部和尾部区域出现了凹坑和凸起，加工表面比较粗糙，原因是此处区域内相邻刀心点法向量的偏差较大，未实现平滑过渡。利用“自动比较”功能与标准件进行对比，观察工件表面的过切和欠切情况，对比结果如图15所示，对应的颜色公差带示意图如图16所示。从对比结果可见，大部分区域的补偿效果较好，误差在0.01 mm以下。图中的区域1与区域2误差较大，分别在0.2 mm和0.5 mm以上，补偿不均匀，局部区域出现误差过大的现象。

(2)法向量光顺后的仿真

对经过方向一致性调整后的法向量进行光顺处理，实现全局法向量的平滑过渡。将经过光顺调整后的法向量作为对应刀心点半径补偿的方向，采用磨损刀具进行仿真，并利用“自动比较”功能与标准件进行比较，得到图17所示的结果，对应的颜色公差带如图16所示。

图16和图17显示，鞋楦表面大部分误差位于0.01 mm以下，只有小部分区域误差介于0.01 mm ～0.05 mm之间。整个鞋楦表面误差分布较均匀，鞋楦头部、中部、尾部都得到了很好的补偿，表面光滑。补偿均匀的原因在于法向量经过光顺后实现了平滑过渡，能够保证补偿后的刀心点实现平滑过渡。仿真结果表明了对以刀心点法向量为半径补偿方向的改进算法的有效性。

5 结束语

本文以鞋楦五轴数控加工中的刀具半径补偿为主要研究内容，针对将刀心点法向量作为半径补偿方向时求出的法向量方向局部可能发生突变的问题，提出一种全局法向量光顺方法。将经过方向一致性调整后所得法向量中的异常法向量置零，然后对置零法向量采用线性插值的方式实现所有相邻刀心点法向量的平滑过渡。经仿真验证，将光顺后的法向量作为半径补偿方向加工得到的工件表面光滑性更好，补偿更加均匀。

将刀心点法向量作为刀具半径补偿方向的补偿方法适用于利用截平面法和螺旋线导动法生成的刀位轨迹，同样本文提出的法向量光顺方法除了适用于鞋楦加工，也适用于其他利用截平面法和螺旋线导动法生成的刀位轨迹。

本文提出的刀具半径补偿方法能够有效减小加工误差，但并不能完全消除误差，如何对补偿后的误差进行量化估计并逐步调整补偿方式，以进一步减小加工误差，值得继续深入研究。