无错区分两个任意分布的未知纬线态

吕彦霖， 祝凤荣

(西南交通大学物理科学与技术学院， 成都 611756)

1 引 言

量子通信和量子计算中的许多应用都需要用到量子态分辨，例如：量子秘密共享[1]、量子密钥分发[2]、量子安全直接通信[3]、量子隐形传态[4-6]等. 量子态分辨问题是指许多量子态构成了一个集合，从这个集合中取出一个量子态，如何确定取出的这个量子态是集合中的哪个态. 这不是一个容易解决的问题，因为任意一个未知量子态不可能被精确复制(虽然无法精确复制，但是人们可以实现非精确的量子克隆). 当集合中的量子态互相不正交时，我们无法百分百确定取出的这个态是集合中的哪个态. 在量子态分辨问题中，人们常用的方案主要有两种，分别是最小容错区分(测量结果可能会出错，但是需确保出错概率取到最低)和最优无错区分(测量结果不会出错，但可能会出现测量结果不能确定待确定态是哪个态的结果，并且需确保出现这种结果的概率取到最低).

为了对两个未知态进行无错分辨，2005年Bergou和Hillery[7]设计了一种可编程的量子分辨器. 该设备可以在不知道这两个态信息的条件下，分辨出数据寄存器中的待确定态.这样的可编程设备由两个程序寄存器A、C和一个数据寄存器B构成，假设程序寄存器A和C中分别储存着量子比特态|ψ1>和|ψ2>，数据寄存器B中储存着待确定态|ψ?>(|ψ?>是|ψ1>和|ψ2>中的一个，先验概率分别为η1和η2，且η1+η2=1), 则可编程量子分辨器的主要作用是分辨下面两个总输入态：

|Ψ1>=|ψ1>A|ψ1>B|ψ2>C

|Ψ2>=|ψ1>A|ψ2>B|ψ2>C

(1)

这个分辨器能够以某种成功概率告诉我们待确定态|ψ?>与|ψ1>和|ψ2>中的哪一个相同，所以对两个未知态的最优无错区分问题其实就是针对这两个态寻找最优的无歧分辨器. 可编程的量子分辨器就是一个可编程的量子测量器，在数学上有一个全局广义测量与其对应，因此我们可以通过一组广义测量算符来表示它.量子态分辨问题其实就是针对不同类型的态寻找最优的测量算符, 并且计算出与其对应的最大成功概率.

上面介绍的这个分辨器中的输入态|ψ1>和|ψ2>都是量子比特态，也就是二维单拷贝的. 在这个分辨器提出之后，人们又对其进行了实验实现和进一步的推广，将输入态|ψ1>和|ψ2>推广到了都是高维单拷贝的情况[8]和高维任意多拷贝的情况[9-10]. 此外，人们还研究了如何无错区分N个未知纯量子比特态的问题[11]、有关无错区分三个线性无关对称态的问题[12].

本文要区分的两个态是纬线态，它是一种特殊类型的量子比特态，它不像一般量子比特态那样分布在整个态空间，而是被限制在了布洛赫球体的某一纬度线上. 它可以表示为

(2)

其中，θ是取值范围[0,π]中的一个常数，φ是取值范围[0,2π)中的未知数. 它在这个范围内任意一点出现的概率服从任意的概率密度函数σ(φ)，所以我们要区分的两个未知纬线态是:

(3)

其中，φ1和φ2是取值范围[0,2π)中的未知数，它们服从相同的任意概率密度函数σ(φ).

2 测量算符与成功概率的推导

我们实际要无错区分的两个总输入态为：

|Ψ1>=|ψ1>A|ψ1>B|ψ2>C

|Ψ2>=|ψ1>A|ψ2>B|ψ2>C

(4)

这里的|Ψ1>和|Ψ2>都是8维空间中的态，解决这个问题所用到的广义测量(POVM)应当也是在8维空间中进行的. 为了便于在实验上实现这个广义测量，我们可以利用Neumark定理和可编程量子态分辨器的光学实现方法[13]，在一个更大的希尔伯特空间上作正交测量. 首先，我们介绍一个扩大的希尔伯特空间，这个空间是10维的，设:

|000>→|e1>,|010>→|e2>,|001>→|e3>,

|100>→|e4>,|101>→|e6>,|110>→|e7>,

|011>→|e8>,|111>→|e10>

(5)

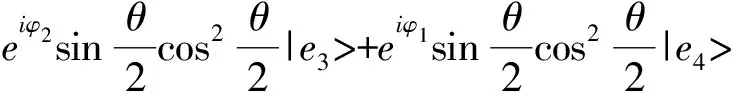
(6)

(7)

其中,

(8)

图1 区分和的分辨器的光学实现

(9)

其中U4(ω)表示为(其推导见第三部分):

(10)

通过U10(ω)，我们可以得到|Ψi>的输出表示：

(11)

(12)

由此，我们可以在输出端定义测量算符：

(13)

(14)

令cos2ω=x，则x的取值范围为[0,1]，此时P(ω)可以表示为

(15)

(16)

(17)

通过U10(ω)我们可以在输入端表示出式(13)定义的测量算符

(18)

(19)

经过计算可知：

(20)

则式(17)表示的成功概率对应的测量算符在|ijk>(i,j,k=0,1)张成的8维子空间中可以表示为:

(21)

文献[14]中讨论的问题是如何最优无错区分两个均匀分布的未知纬线态，得到的最优测量算符为

(22)

这与本文得到的测量算符一致.

3 U4(ω)的推导

(23)

图2 区分和的分辨器的光学实现Fig.2 Optical realization of the discriminator between

图3 U2的光学实现Fig.3 Optical realization of U2

(24)

在干涉仪中，分束仪起的作用可以通过一个二维实变换来表示：

(25)

下面我们来求U4的具体表示.

(26)

(27)

则，式(26)可以表示为：

(28)

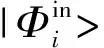
(29)

(30)

4 结 论

我们研究了针对两个任意分布的未知纬线态的可编程无错分辨器，得到了测量算符的具体表达式和对应的成功概率，这对于构造可编程分辨器来说具有重要参考意义. 本文得到的测量算符可以无错区分两个任意分布的未知纬线态，但是不能确定是否是最优的. 文献[14]中严格推导了当σ(φ)取均匀分布对应的1/2π时的最优测量算符的表达式，这个表达式与本文得到的测量算符相同，这说明，本文得到的测量算符对于无错区分两个均匀分布的未知纬线态来说是最优的.