基于自适应MCMC采样的新型UPFNN铝电解能耗模型

丁 伟, 姚立忠2,, 龙 伟, 李炎炎

(1. 四川大学机械工程学院, 成都 610065;2. 重庆科技学院电气工程学院, 重庆 401331)

1 引 言

电解铝产品已广泛应用于航天、交通、建筑、机械制造等重要领域,在世界工业发展过程中占有举足轻重的战略地位[1].据统计结果分析,在消耗方面,2019年我国电解铝消费量为3 672万吨,同比增长2.4%[2].然而,我国铝电解工业已进入到技术瓶颈期,其主要原因是铝电解能耗过高.由于铝电解工艺制造系统具有波动性、动态时变以及不确定性等特征,故难以准确地建立相对动态平稳的铝电解能耗模型,从而导致部分企业无法根据此模型来对未来状况进行整体规划和技术优化.因此,研究高精度铝电解能耗建模技术对工业生产提质增效具有重要意义.

铝电解系统存在一系列的物理化学反应,机理复杂不易量化.因神经网络[3]可处理系统机理未知的建模问题而备受关注.文献[4]使用小波神经网络来研究分析铝电解槽过程中各状态阶段;文献[5]介绍了神经网络控制技术与预测技术结合来调整氧化铝浓度的控制策略.然而,当传统神经网络建模完成时,其权值和阈值将保持不变.当铝电解系统工艺参数因实时工况变化而改变时,基于先前数据所建立的静态神经网络模型将无法满足铝电解工艺条件动态优化的需求.因此,为保证能耗模型对铝电解制造系统运行规律具有一定的渐进学习能力,可引进滤波技术来实时更新系统模型参数.

现如今大多数论文引入扩展卡尔曼滤波(Extended Kalman Filter, UKF)和无迹卡尔曼滤波(Unscented Kalman Filter, UKF)对神经网络的权值阈值进行动态调整.相比于静态神经网络模型,EKFNN与UKFNN所建立的模型能够随工艺条件的改变而实时变化,具有良好的渐进学习能力.文献[6]采用改进无迹卡尔曼优化神经网络来提高建模精度;文献[7]将神经网络、扩展卡尔曼滤波器和递归最小二乘法结合进行参数估计;文献[8]提出一种基于自适应扩展卡尔曼滤波器的径向基函数神经网络;Yao等[9]提出一种基于强跟踪UKF的改进前馈神经网络算法,用于建立铝电解能耗模型;文献[10]将人工神经网络和UKF结合对非线性系统进行状态估计.

根据上述文献分析可知,EKFNN与UKFNN有效拓展了铝电解能耗建模技术,但上述技术往往限定了高斯、低维环境的假设条件,缺乏对高维非线性非高斯系统能耗建模技术的探讨,而实际上铝电解系统具有噪声密集、分布类型未知且参数高维等特征.因无迹粒子滤波具有典型处理非线性非高斯问题的能力,故本文在无迹粒子滤波(Unscented Particle Filter, UPF)渐进更新神经网络权值阈值[11]的构建框架下,为进一步使算法适应于高维数据,通过改善无迹变换(UT)中κ参数来优化采样过程.同时,为避免该算法中粒子状态出现多样性损失,本文在传统马尔科夫链蒙特卡洛(MCMC)方法[12-13]基础上引入自适应采样策略来保持粒子的多样性,精调模型状态逼近真实运行系统的贴近程度.

综上所述,本文提出一种基于自适应马尔科夫链蒙特卡洛采样的新型无迹粒子滤波神经网络(Adaptive Markov Chain Monte Carlo Unscented Particle Filter Neural Network, AMCMC-UPFNN)算法,并用此来建立铝电解能耗模型.该技术有望提高铝电解能耗建模精度不佳的难题,可作为铝电解未来能耗预测的有效方法.最后，以重庆某铝厂电解车间工艺系统为例,采集9种主要决策变量数据进行铝电解能耗建模,验证了所研究的科学性与有效性.

2 基于自适应MCMC的新型无迹粒子滤波神经网络

2.1 滤波方程

在传统神经网络建模[6]基础上,为动态描述滤波方法对神经网络权值阈值的更新过程,使用状态空间表示法建立滤波方程[14-15],如式(1)所示.

(1)

其中,ωk表示k时刻状态变量(即神经网络权值阈值)；uk表示k时刻某工业制造系统的输入变量；yk表示k时刻量测变量(即评价工业制造系统优劣的输出变量).假设系统测量噪声vk为0均值高斯噪声,方差为R;系统过程噪声为0均值高斯噪声,方差为Q.第k时刻的网络权值依赖于k-1时刻的网络权值以及系统随机过程噪声θk,而测量噪声主要来描述系统因传感器等装置导致的建模误差.非线性测量函数h(·)使用一个多层感知器来近似,其表达式如式(2)所示.

(2)

2.2 自适应MCMC-UPFNN算法描述

2.2.1 新型UPFNN算法描述 在工业系统过程建模中,通常将环境扰动变量和内部状态变量简单地看成是相对稳定的.但是,在实际的工业过程中,由于“人、机、料、法、环”等诸多不确定因素的存在,使得由决策变量建立的静态神经网络模型难以适应真实工艺.本文则以UPFNN为研究对象,将神经网络的权值阈值作为UPFNN的状态变量,将神经网络的输出作为UPFNN的量测变量,具体UPFNN算法可参见文献[16].

UPFNN的算法精度主要取决于无迹粒子滤波器,然而在高维情况下会发生算法会发散现象,从而导致算法精度显著下降.为解决该问题,本文改进了无迹变换(Unscented Transformation, UT),将常规项κ由平方项κ2代替,改进后的无迹变换能够有效地避免数据高维而导致UT矩阵出现负定情况,进而保证UT采样的正确性.其中，UPFNN的UT采样过程,如式(3)所示.

(3)

λ=α2(N+κ2)-N

(4)

从改进后的UT表达式可以看出,新型UPFNN算法通过调整κ参数,确保在高维环境下UT矩阵的非负定性和算法的稳定性,并通过UT得到的采样点及其相应权重建立的概率密度分布更加接近制造系统真实状态的概率密度分布.

2.2.2 自适应MCMC方法描述 无迹粒子滤波本质上属于粒子滤波理论[17-18]的范畴,随着时间更新UPFNN算法中粒子种类会逐渐减少,从而引起粒子多样性损失问题.而MCMC方法是在贝叶斯理论框架下提出,通过计算机进行模拟满足Markov序列的Monte Carlo方法,实现抽样分布随模拟的进行而改变的动态模拟.因此,MCMC在粒子重采样后能使粒子保持多样性而不影响近似有效性.

MCMC理论中最核心部分是采样粒子时的接受概率[19],但粒子多样性会随着更新迭代而逐渐减少,故要求在保证粒子多样性的前提下,尽可能保持原有粒子的真实状态,从而使所建立的概率密度分布更接近真实分布.对此,本文提出了如式(5)的表达式,该表达式能够根据粒子迭代次数来调整接受概率,更新前期粒子种类足够多,此时接受概率可以小一些;随着更新迭代,后期接受概率要大一些,使粒子的种类增加,以防止粒子多样性损失.

(5)

2.2.3 自适应MCMC-UPFNN算法设计及分析基于上述新型UPF算法、自适应MCMC理论和神经网络,本文提出一种基于自适应MCMC采样的新型无迹粒子滤波神经网络即AMCMC-UPFNN算法.

基于式(1)的滤波方程,AMCMC-UPFNN流程如下.

(2) 时间更新.根据式(3)进行UT采样,通过得到的采样点及其相应权重计算统计量y.

(6)

(7)

(8)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

若Neff≤Nth(Neff为有效粒子数,Nth为设定的阈值,一般取为N/3)则说明粒子的权值已经退化严重,需要进行重要性重采样;否则直接进入下一步骤.

(5) MCMC过程.根据式(5)的接受概率来产生新的粒子:

(a) 若接受,则

(a) 平均绝对误差MAE

(a) PFNN (b) UPFNN

(16)

(b) 若否则拒绝,则

(b) 平均相对误差MRE

(17)

(6) 结果输出.

(18)

3 铝电解能耗建模应用实验

3.1 实验对象

本文将重庆某电解铝制造车间异型阴极和穿孔阳极联合使用的新型铝电解装备作为实验对象[12],如图1所示.其中，f1表示吨铝直流能耗,原则上希望其数值越小越好.

根据专家的经验，以及我们对电解铝制造系统的工艺参数的分析,得出影响吨铝直流电耗的系列参数有如下过程工艺变量:系列电流、分子比、铝水平、电解质水平、槽温度、出铝量、氟化盐日用量、下料间隔和槽压.基于工厂计算机测控系统对电解槽进行日报数据采样得到上述工艺数据样本773 组,如表1所示.利用这些实测样本和本文所开发的算法开展铝电解制造系统单位直流能耗的建模分析与研究.

3.2 基于AMCMC-UPFNN的建模及结果分析

为验证AMCMC-UPFNN算法的有效性和优越性,本文在相同的数据样本及仿真平台(MATLABR2014b)条件下,对比预测误差来衡量算法性能.所有实验均将表1中773组铝电解数据分成训练集样本700组和检验集样本73组,其中采用9-9-1的神经网络结构,输入为9种决策参数,输出为单位能耗,隐含层传递函数为Sigmoid函数,输出层传递函数为Purelin函数.

依据PFNN、UPFNN、MCMC-UPFNN和AMCMC-UPFNN建立铝电解工艺能耗模型,如图2所示.为了清楚地分析模型优劣,4种模型预测能耗相对误差对比如图3.从曲线的拟合效果可看出,AMCMC-UPFNN拟合效果都远远优于其他模型.整体来看,根据调整后的无迹变换所建立的模型性能均优于其他模型,凸显了其优越性,并且自适应MCMC对于算法的优化是可行的.

图3 模型能耗相对误差对比图Fig.3 Comparison of relative error of model energy consumption

从方法上而言,调整后的UT使算法可适用于高维数据的场合,提高了算法的鲁棒性;通过引入自适应MCMC克服了算法中粒子多样性损失问题,提高了模型的精度.从图3可看出,AMCMC-UPFNN相对误差百分比不超过1%,取得了比PFNN、UPFNN和MCMC-UPFNN更优的性能指标.各模型建立能耗模型的指标数据对比见表2.

表2 不同模型相关性能指标比较

从表2可知，就模型精度而言,很明显AMCMC-UPFNN的各项绝对误差指标都低于PFNN、UPFNN和MCMC-UPFNN.特别是,AMCMC-UPFNN模型的SSE、MSE和RMSE明显低于其他3种方法,进而验证了AMCMC-UPFNN方法的有效性.

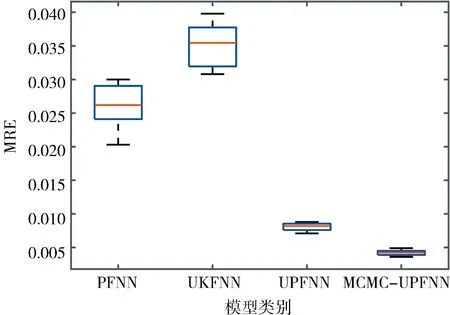
为了避免随机化初始值对模型评估的偶然影响,本文基于各模型分别对能耗预测进行20次独立重复实验,然后统计实验结果的相关性能指标,并通过箱线图的形式展示了AMCMC-UPFNN能耗模型良好的稳定性,如图4所示.

(c) 相关系数R

4 结 论

本文提出了一种基于自适应MCMC采样的新型无迹粒子滤波神经网络(AMCMC-UPFNN)算法,以无迹粒子滤波神经网络为研究对象,利用无迹变换(UT)中κ参数的平方项代替UPFNN算法中对应的常规项;然后,引入自适应MCMC来解决UPFNN中粒子多样性损失问题;最后本文系统性地呈现了AMCMC-UPFNN算法框架并构建了铝电解能耗模型.通过对PFNN、PFNN、MCMC-UPFNN和AMCMC-UPFNN建立的铝电解能耗模型进行对比实验验证.结果证实了利用AMCMC-UPFNN算法所建模型精度高和自适应能力强.因此,本研究为利用滤波神经网络进行建模提供了新的思路和方法.在未来研究过程中,将进一步探索滤波理论与深度神经网络学习算法的融合策略来进一步挖掘铝电解制造系统的隐藏运行规律.