基于图像多尺度分解的前景提取

王 斌， 何 坤， 王 丹

(四川大学计算机学院， 成都 610065)

1 引 言

图像前景是指图像中用户感兴趣的语义对象，该对象是分析和理解图像内容的基础.由于图像内容理解受限于用户认知，因此其前景因人而异.为了提取用户指定的前景，研究者结合用户交互，根据图像低层特征提出了大量的算法，如随机游走[1]，水平集方法[2-4]和图论技术[5]等. 然而，图像中的纹理、弱边缘和低对比度使得现有算法难以得到理想结果.

近年来，深度学习[6-7]通过训练卷积神经网络自适应地从训练集中挖掘图像的多尺度特征，并成功运用于图像前景提取.但是，深度学习需要海量的前景样本训练神经网络参数，而实际上，前景样本数量是有限的，这导致深度学习的前景提取效果较差.同时，该方法不能成功提取训练集中未包含的前景，因为缺乏学习样本.

基于图论的前景提取模型利用图像边缘和前、背景颜色分布构建了能量泛函，运用图割算法从图像中提取前景. 现有前、背景颜色分布模型可分为局部直方图[8-9]和高斯混合模型[10]，前者虽然显式表示为前、背景像素的亮度分布，但其准确性依赖于人机交互量和图像亮度分布.相比于前者，高斯混合模型极大简化了用户交互量，它将前、背景像素颜色分布表示为固定个数的高斯函数加权和[10].每个区域的像素分布对应一个高斯函数，其参数在前景提取过程中估计区域像素的一阶原点矩和二阶中心矩.高斯混合模型可有效刻画卡通图像的前、背景颜色分布，但对于自然图像其准确性受到纹理的负面影响.其原因是：1) 纹理加剧了区域颜色变化，降低了二阶中心矩估计精度；2) 纹理恶化了区域间颜色的显著差异，减少了不同区域的一阶原点矩的距离；3) 固定高斯个数导致了高斯混合模型负面影响.针对1)和2)，文献[11]引入了基于超像素抑制了纹理对前景提取的影响，针对3)文献[12]在分割之前使用聚类算法分析前景和背景中的区域数目，避免了不恰当高斯个数对前景提取的负面影响.

基于图割的方法利用边缘和区域分布特征提取前景，但提取质量敏感于特征尺度，即细尺度的局部最优和粗糙尺度较差的提取精度.为了从恰当尺度提取前景，本文将图割与多尺度分解相结合，运用全变分正则化[13]将一副图像分解为一系列平滑图像.该平滑模型既保护了图像边缘，又消除了区域非均匀性，有助于提升区域分布参数估计准确性.对于每个平滑图像，前、背景颜色分布分别表示为优化的高斯混合模型(即OGMMs).在每个OGMMs中，运用直方图形状分析方法估计高斯函数个数.结合OGMMs和多尺度分解，本文将前景提取任务转换为分割和分解尺度的联合优化，通过分割和多尺度分解的交互，从适当的尺度提取前景.

2 本文模型

人眼观察图像时，图像信息被理解为一定尺度上有意义的内容.因此，我们将一幅图像分解成一系列具有不同分解尺度的平滑图像，保留了图像的边缘并消除了图像非均匀性.对于每个平滑图像，采用直方图形状分析方法对其颜色分布进行准确建模.结合GrabCut和平滑图像的颜色分布模型，将前景提取转换为分割和分解尺度的联合优化.一副具有N个像素的图像u0:Ω→(uR,uG,uB)被初始矩形框划分为背景区域TB和带有少量背景像素的前景区域TF.分割结果表示为x=(x1,…,xi,…,xN)，其中，xi=1表示前景，xi=0表示背景.其前景提取的能量泛函为

(1)

式中，第一项M(u,u0)是图像多尺度分解，u为平滑图像；第二项为平滑图像的前景提取，ω表示前、背景颜色分布参数，该项S(x,ω,u)表示为

S(x,ω,u)=U(x,ω,u)+V(x,u)

(2)

式中，U(x,ω,u)为参数ω下x对平滑图像u的分割结果评价；V(x,u)定义为将分割曲线放置在前景边界上的惩罚，如下式

exp(-β(u(i)-u(j))2)

(3)

式中，Λi是第i个像素的相邻像素集；dis(·)表示像素对的欧几里得距离；[·]是指示函数.根据文献[5]，本文γ=50.为确保式(3)的能量在低梯度时较大，而在高梯度时较小，其β如下式.

β=0.5〈(u(i)-u(j))2〉-1

(4)

式中，〈·〉表示均值.

2.1 多尺度分解

式(1)的最优解依赖于平滑图像的颜色分布参数，但该参数对分解尺度敏感.如，在细尺度平滑图像中，残留的纹理信息导致参数估计精度较差.在粗糙尺度上，图像被过度平滑，估计的参数不能近似颜色分布.为了获得具有适当尺度的颜色分布模型，我们根据全变分正则化将图像分解为一系列平滑图像，即最小化下述问题.

(5)

式中，第一项为数据保真项，用于保护图像边缘特征；第二项为正则项，用于平滑图像非均匀区域；λ为保边平滑参数. 假设(5)存在最小解，其解满足欧拉-拉格朗日方程.

(6)

运用后向差分方法和固定点迭代算法，平滑图像uk(i)可离散计算为

(7)

其中，

ϖ(k)(j)=|∇uk-1(j)|-1

(8)

在式(7)中，平滑图像uk依赖于u0和uk-1，前者有利于保留图像边缘，而后者则有利于平滑非均匀区域.通过迭代计算，图像被分解为一系列平滑图像.随着迭代次数的增加，分解尺度不断增加，图像中非均匀区域也会逐渐趋于平滑.

假设平滑图像中每个区域颜色分布紧凑，区域颜色分布可表示为高斯函数.以第m个区域为例：

G(μm,∑m,u(i))=

(9)

式中，μ(m)和∑(m)分别是该区域颜色分布的均值向量和协方差矩阵.假设前景和背景中区域个数已知，前景和背景表象可表示为高斯混合模型.其参数ω={ωF,ωB}为

(10)

式中，π(m)表示第m个区域的面积系数；nF和nB分别表示前、背景区域个数.

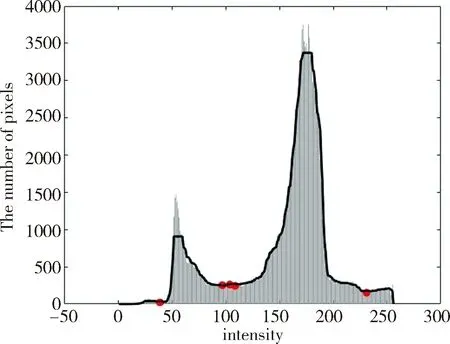
为了检测直方图形状波谷，本文分析直方图Hs后向差分的符号，其符号Sgn(·)，如下式.

(11)

δ(·)是后向差分算子，且波谷处亮度为

(12)

利用波谷v=(v1,v2,…,vn)将图像分为n个区域，结合分割曲线可计算出前景和背景中区域个数.在已知参数ω的前提下，像素u(i)属于前景或背景的可能性为

(13)

式(2)中数据项U(·)可计算为

log(LB(x,ωB,u(i))))

(14)

2.3 前景提取算法

在式(1)中，如果α→0，该模型等效于原始图像的前景提取；如果β→0，该式简化为多尺度分解.为了抑制纹理对前景提取质量的影响，本文设置α=β=1. 式(1)可简化为

U(x,ωk,uk)}},k=0,1,…

(15)

(15) 式的最优结果可以通过分割和颜色分布参数的交替优化得到，如图1所示.对于给定平滑图像uk，(15)式中V(x,uk)仅需计算一次且可以重复使用.由于前景区域中存在一些背景像素，前景提取过程中应更新数据项U(x,ωk,uk).因此，(15)式的最优解通过交替执行以下步骤得到：(1) 给定颜色分布参数ω，利用最大流算法[14]计算分割结果x；(2) 给定分割结果x，运用EM算法更新参数ω.在此交替优化过程中，参数ω的估计精度得到进一步的提升，前景区域中的背景像素被逐渐剔除，其能量逐步降低并趋于收敛，如图1(b)所示.为了评价每个平滑图像的前景提取性能，本文基于相邻尺度上提取的前景定义了一个相似性指标，如下.

(16)

式中，card(·)统计像素点个数.

(15)式的最优解不仅依赖于平滑图像的边缘和颜色分布，还取决于分解尺度.在细尺度下，图像中残余的非均匀性导致前、背景颜色分布参数估计精度较差.随着分解尺度增大，残余非均匀性被逐渐消除，前景边界得到保留，提取性能不断提升，相似度保持不减.在粗尺度下，图像被过度平滑，使前景和背景之间产生伪重叠效应，提取性能较差，相似性不增，如图1(e)所示.根据相似性随分解尺度的变化，本文在满足下述约束条件时找到合适的尺度进行前景提取.

Sm(k)≤Sm(k-1)

(17)

本文将图像分解为一系列平滑图像，对每幅平滑图像首先运用直方图形状分析方法估计前景和背景的区域数目，然后通过分割和颜色分布参数的交替优化提取前景.根据相邻尺度上分割结果计算其相似性，当满足迭代终止条件时算法停止，其算法流程如图2所示.

图2 本文模型的流程Fig.2 The flowchart of the proposed model

3 实验及分析

基于多尺度分解的前景提取模型由图像分解和GrabCut两部分构成，在图像分解过程中引入参数λ.为了分析参数λ对前景提取性能的影响，对一副来自BSD300数据集的480×320像素图像选用不同的λ值进行平滑处理，部分平滑图像以及对应的分割结果如图3所示.当λ=100.0时，平滑图像中残余的非均匀性导致过分割现象，如图3(b)所示.当λ=0.001时，图像被过度平滑从而导致欠分割效果，如图3(d)所示.不同参数λ平滑处理图像的前景提取评测分数如表1所示.依据表1，该参数在接近0.1时取得较为理想的结果.

表1 不同参数λ的评测分数

为了抑制纹理对平滑图像前、背景中区域个数估计的影响，本文运用中值滤波对平滑图像亮度直方图平滑处理.为了分析中值滤波参数s对前景提取性能的影响，对一副来自iCoseg数据集的332×500像素的人物图像选用不同的s值进行直方图形状分析，部分前景提取结果如图4所示.当s=5时，平滑后的直方图中仍然存在大量伪谷，导致前景提取效果较差，如图4(b)所示.当s=29时，存在多个区域被错误合并为一个区域，降低了前景提取效果，如图4(d)所示.不同参数s滤波处理图像的前景提取评测分数如表2所示.依据表2，该参数取为17.

表2 不同参数s的评测分数

为了测评本文算法的有效性,并与传统GrabCut[10],MIS[15]以及Deep GrabCut[16]进行比较，对图5所示的自然图像进行前景提取，其评测分数如表3所示.其中，GrabCut[10]使用固定高斯个数的高斯混合模型对图像前、背景区域颜色分布进行统计建模，并基于原始图像的参数估计和分割的交替优化提取前景，其前景提取效果受到高斯函数个数以及原始图像中纹理、噪声等的影响.

表3 图5所示图像的评测分数

MIS[15]将多尺度分解和水平集算法相结合，在多尺度边缘的约束下提取前景.Deep GrabCut[16]将矩形框转换为一个欧式距离图，然后将该图与RGB图像组合起来作为卷积编码-解码网络的输入，以前景预测为最终输出.对于近似卡通图像，4种算法提取的前景在视觉上无差异，如图5(a)所示.然而，与传统GrabCut相比，本文运用直方图形状分析方法自适应估计了高斯个数，弥补了传统GrabCut采用固定高斯个数的不足，得到了更准确的提取结果，如图5(b)所示.此外，本文引入TV模型对图像进行保边平滑处理，基于不同尺度的边缘和颜色分布模型从适当的尺度提取前景，对于含有纹理的图像，本文算法提取结果在视觉上优于GrabCut算法，如图5(c)～5(d)所示.

相对于MIS，本文算法增加了不同分解尺度的图像颜色分布特征，弥补了利用多尺度边缘特征对含有弱边缘图像前景提取的不足，改善了前景提取效果，如图5(c)所示.

Deep GrabCut[16]在PASCAL数据集上进行训练并学习20种对象的特征，其前景提取性能依赖于该训练集中对象的类别.相比而言，本文基于图像多尺度边缘和颜色分布特征，在提取该训练集不包含的前景时，取得了相对更优的结果，如图5(c)所示.

本文提出了基于多尺度分解的前景提取模型，有效克服了图像纹理细节对高斯混合模型参数估计的负面影响；运用直方图形状分析方法弥补了不恰当的高斯数目对前景提取造成的不良影响；结合不同尺度的边缘和区域颜色分布从恰当尺度提取前景. 然而，图像多尺度分解过程中只保护了边缘而不能增强弱边缘，因此后续工作设计新的非线性平滑增强弱边缘，进一步提高前景提取质量.