噪声环境下神经元集群的同步放电
宋 辞,焦贤发
(合肥工业大学 数学学院,安徽 合肥 230601)
大脑正常的认知功能与异常的神经激化都与神经振子同步放电密切相关[1]。近年来,越来越多的神经动力学研究人员关注耦合神经振子集群的振荡同步活动。文献[2]和文献[3]通过对数据进行分析,认为神经振子的振荡为神经细胞间信息编码、信息访问以及检索皮层编码等提供了基础,进一步证明了振荡是视神经细胞间的通讯形式。研究人员通过大量的实验证明,神经振子集群的同步振荡是神经振子在大脑的不同皮层间独特的信息整合机制,正常的生理活动与生理病症(如帕金森等)都是与神经元集群的同步振荡有关[4-5]。文献[6]和文献[7-8]将神经振子的振荡简化成极限环运动,而神经振子集群则模拟成相互耦合的神经振子组成的神经网络;为了便于模型的数学处理与分析,将神经振子的振幅和神经振子间的耦合强度定为常数;研究表明在弱噪声极限下,神经振子集群双稳态,刺激会使神经振子的平均振荡频率发生偏移。
当高等动物的感官(如眼睛、耳朵)受到刺激,大脑中的神经振子就会对刺激产生响应;神经振子通过对动作电位编码进行信息传递。文献[5]通过对猫的视觉皮层神经振子刺激实验,证实了刺激强度和刺激频率会影响神经振子集群的同步活动;文献[9]利用相位敏感函数建立了神经振子集群的动态演化模型,数值模拟表明,外部周期性刺激的强度和频率改变都会影响神经振子集群的同步放电模式。
在真实神经系统中噪声是无处不在的[10-14],神经系统中的噪声可分为背景噪声(加性噪声)以及与信号有关的噪声(乘性噪声)。背景噪声如离子通道的随机开启或关闭引起的噪声(离子通道电导噪声、离子通道散粒噪声、离子泵噪声)、突触噪声(释放神经递质的数量变化、神经递质的化学反应、神经递质的释放以及配基门控的开合产生的噪声)、各种分子的运动产生的热噪声、相邻神经元活动的电磁影响[13];信号相关的噪声如输入信号形状、时间随机性产生的噪声[14]。噪声可以改善神经元在接受强信号时发生的畸变[15]以及优化哺乳动物的神经系统对于信号的响应[16]。在医学研究中,越来越多的研究人员用噪声去改善神经激化的异常放电活动,例如帕金森、听觉改善、平衡控制、视力提升以及视网膜修复等[17-20]。
刺激和噪声的研究中,不仅实验研究引起人们的重视,神经振子模型的研究也受到极大的关注。文献[9]通过建立神经振子的动态模型,在神经元集群的同步运动过程中,考虑了刺激和背景噪声共同作用下神经振子的同步放电行为,但只考虑了刺激改变对神经元集群同步运动的影响。
相响应曲线有2种不同的形状,文献[21]建立相位振子模型,利用约束优化的欧拉-拉格朗日法找到最小李雅普诺夫指数的相响应曲线,分析刺激和加性噪声对非耦合噪声驱动神经元集群同步的影响,研究表明,不同形状相响应曲线的神经元集群对同步的敏感度不同;文献[22]建立刺激、信号噪声与背景噪声共同作用下的Wiener-type神经元集群同步运动模型,噪声的介入使得神经元输出更多峰值,增加感知神经对信号的识别能力。
本文建立具有外部周期刺激和混合噪声作用下的耦合神经振子集群的相位演化模型,分析刺激强度、刺激频率、背景噪声和信号噪声对神经振子集群的同步活动的影响。
1 数学模型
考虑在刺激、噪声的共同作用下,由N个全局耦合的神经振子组成的神经振子群演化动力学方程:
Isin(ct)S(ψi)+G(ψi)ηi(t)+ξi(t)
(1)
其中:ψi、ψj分别为神经振子i和j的相位;K0为任意2个不同神经振子间耦合强度,这里为一恒定常数;ω为在无相互作用下及外刺激作用下单个神经振子的特征频率;K0M(ψj-ψi)为神经振子i和j之间的相互作用项;Isin(ct)S(ψi)为神经振子i对刺激的响应,I表示刺激强度,sin(ct)表示神经振子受到的刺激形式为谐波刺激,c表示刺激产生的频率;G(ψi)ηi(t)为乘性噪声;ξi(t)为加性噪声,乘性噪声与电信号相关。
为表达方便,记
Γ(ψj-ψi)=ω+K0M(ψj-ψi)+
Isin(ct)S(ψi)
(2)
为了方便起见,将η(t)和ξ(t)模拟为零均值、σ相关的的高斯白噪声,A为乘性噪声的强度,B为加性噪声的强度。即:
〈ηi(t)〉=0,〈ηi(t)ηj(t)〉=2Aδijδ(t-t′),
〈ξi(t)〉=0,〈ξi(t)ξj(t)〉=2Bδijδ(t-t′),
〈ηi(t)ξj(t)〉=0
(3)
结合文献[23-24]的FPK公式推导,可以得到相应于方程(1)的Fokker-Planck方程:
(4)
(4)式中的密度函数f(ψ1…ψN;t)dψ1…dψN表示相位ψi落入区间(ψi,ψi+dψi)的概率,i=1,2,…,N。记
H(ψj-ψi)=Γ(ψi,ψj)+AG(ψi)G′(ψi)
(5)
定义最有可能具有相同相位ψ神经振子数密度:
(6)
考虑到神经系统的随机性,引入平均数密度如下:
n(ψ1…ψN;ψ)=
(7)
根据(5)式~(7)式,对平均数密度关于t求偏导,化简得:
(8)
求偏微分方程(8)的数值解,考虑以下2个边界条件:
(1)周期条件。对任意t,有
n(0,t)=n(2π,t)
(9)
(2)归一化条件。具体表示为:
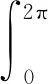
(10)
由于H(ψ)、S(ψ)、,Γ(ψ)和G(ψ)都是以2π为周期的周期函数,为了数值分析的需要,可将它们展开为傅里叶级数。
为简便起见,只取M(ψj-ψi)=sin(ψj-ψi),S(ψj-ψi)=sin(ψi),G(ψi)=sin(ψi)。这种形式比较符合Hebb学习律,即当2个神经振子相位相同时,耦合强度增长最快;当2个神经振子相位相反时,耦合强度下降最快。
2 数值分析
2.1 改变单一噪声对神经元集群同步的影响
为研究信号噪声和背景噪声对神经振子集群动力学行为的影响,考虑在相同的刺激条件下,增加信号噪声强度和加性噪声强度导致神经振子集群放电密度的变化,如图1所示。

图1 单一噪声环境下改变噪声神经振子集群放电密度随时间的演化
图1a中的参数为:ω=π,B=0,I=200,c=0.01;图1b中的参数为:ω=π,A=0,I=200,c=0.01。
刺激强度和频率保持不变,乘性噪声增加,神经振子集群放电密度峰值减小,这表明乘性噪声的增加对神经振子集群的同步进行抑制(图1a);刺激强度和频率保持不变,加性噪声的增加,神经振子集群放电密度峰值降低,振荡更加强烈,这表明加性噪声会使得神经振子集群的振荡更加剧烈(图1b)。
在真实神经系统中,神经振子集群受到混合噪声的影响。将神经振子集群置于不同强度的信号噪声或背景噪声下,观察神经振子集群放电密度的影响,结果如图2所示。
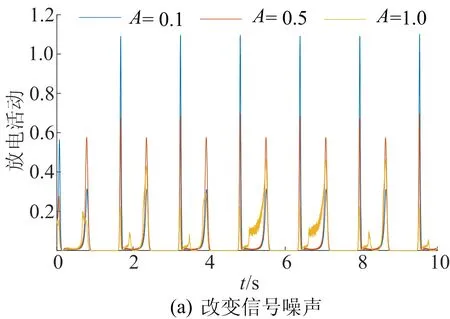
图2 刺激与混合噪声环境下改变噪声神经振子集群放电密度随时间的演化
图2a中的参数为:ω=π,B=1,I=200,c=0.01;图2b中的参数为:ω=π,A=0.1,I=200,c=0.01。
信号噪声强度越大,神经振子集群放电密度的峰值越小;在信号噪声较弱时,神经振子集群的振荡是有序的,信号噪声增强会使得神经振子集群振荡无序(图2a)。背景噪声强度越大,神经振子集群放电密度的峰值越小;在背景噪声较弱时,神经振子集群的振荡是有序的,背景噪声增强会使得神经振子集群振荡无序(图2b)。
由图2可以看出,当神经振子集群置于强乘性噪声和强加性噪声下,周期运动受到噪声的影响产生杂乱的放电密度变化。
当神经振子集群置于强乘性噪声和强加性噪声下,周期运动受到噪声的影响产生杂乱的放电密度变化,如图3所示。

图3 强噪声环境下神经振子集群放电密度随时间的演化
图3a中的参数为:ω=π,A=0.1,B=1,I=200,c=0.01;图3b中的参数为:ω=π,A=0.1,B=2,I=200,c=0.01。
2.2 噪声的刺激改变对神经元集群同步的影响
为研究不同信号噪声环境下,刺激强度改变对神经振子集群同步放电影响,考虑背景噪声和刺激频率不变,改变信号噪声强度和刺激强度,神经振子集群放电密度随时间的演化,如图4所示。

图4 不同信号噪声下改变刺激强度对神经元集群同步的影响
图4a中的参数为:ω=π,A=0,B=0.5,c=0.01;图4b中的参数为:ω=π,A=0.1,B=0.5,c=0.01;图4c中的参数为:ω=π,A=1,B=0.5,c=0.01。
只考虑背景噪声时,随着刺激强度增加,神经振子集群放电密度峰值增加(图4a);在信号噪声较弱时,神经振子集群的放电密度峰值增加更为明显(图4b);而强信号噪声下,随着刺激强度增加,神经振子集群的放电密度峰值增加,振荡频率也增加(图4c)。这表明弱信号噪声增强刺激强度对神经振子集群的同步增益,有利于神经元集群对信号的接收。
在不同信号噪声下,刺激频率改变对神经振子集群同步放电的影响,如图5所示。
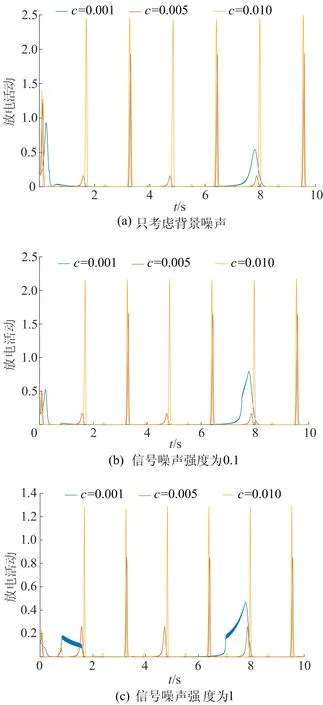
图5 不同信号噪声下改变刺激频率对神经元集群同步的影响
图5a中的参数为:ω=π,A=0,B=0.5,I=200;图5b中的参数为:ω=π,A=0.1,B=0.5,I=200;图5c中的参数为:ω=π,A=1,B=0.5,I=200。
只考虑背景噪声时,随着刺激频率增加,神经振子集群放电密度峰值增加(图5a);在弱信号噪声下,神经振子集群的放电密度峰值增加的幅度减小(图5b),这表明,弱信号噪声减小背景噪声对神经振子集群同步的增益作用;而关联强度很强的信号噪声下,神经振子集群的放电密度峰值增加幅度减少(图5c),振荡频率增加,即强信号噪声减弱背景噪声对神经振子集群的同步的增益,增加神经元集群的振荡频率有利于对神经元集群对信号的接收。
3 结 论
神经元集群同步运动受到刺激和噪声的影响,本文建立受刺激、乘性噪声以及加性噪声影响的神经振子集群同步运动相位演化模型,通过数值模拟,分析在刺激、信号噪声和背景噪声不同影响下的神经振子集群的同步放电活动。数值结果表明,对神经振子集群的刺激和噪声都能对神经振子集群的同步活动产生影响,其中神经振子集群放电密度的峰值会受到刺激的强度、频率以及乘性噪声、背景噪声共同影响;而神经振子集群的放电密度周期则受到刺激的频率影响;噪声会影响到神经振子集群的放电密度变化,无论是信号噪声过强,还是乘性噪声过强,神经振子集群的放电密度都由有序变为无序,神经振子有序的信息传递就会受到影响。

