一种基于Hamming码的门限多秘密共享方案
李富林,刘 杨,王娅如
(合肥工业大学 数学学院,安徽 合肥 230601)
0 引 言
秘密共享是一种将秘密分割储存,以阻止秘密过于集中,保证秘密的安全性和可靠性的密码技术。秘密共享是密码学的一个重要研究分支,被广泛应用于信息安全与数据保密中。门限秘密共享方案又称作阈值秘密共享方案,于1979年由Shamir[1]和 Blalley[2]分别基于 Lagrange 插值多项式和射影几何理论提出。在(k,n)门限秘密共享方案中,分发者将被共享的秘密信息分成n份,并通过安全信道将份额分发给n个参与者,其中任意k个参与者都能恢复秘密,任意k-1个或者更少的参与者无法恢复秘密。实现(k,n)门限秘密共享方案的方法除了以上2种,还包括Karnin-Greene-Hellman[3]矩阵法、Asmuth-Bloom[4]的中国剩余定理法等。文献[1]提出的方案实现简单,计算代价小,并且是一个完备理想方案,得到了广泛的研究和应用。然而传统的秘密共享方案存在着以下不足:① 秘密分发者和参与者并非都是诚实可信的,可能存在一些欺诈行为;② 一次秘密共享过程只能共享一个秘密信息;③ 参与者的秘密份额是一次性的。即当完成一次秘密共享过程,分发者必须通过安全信道重新为参与者分配新的份额来实现新一轮的秘密共享。
近几十年来,秘密共享领域的研究得到了快速的发展。针对欺诈行为,文献[5]提出了可验证秘密共享的概念;文献[6]在此基础之上提出了可公开验证的秘密共享策略的概念,并基于ElGamal的签名策略实现了2个可公开验证的秘密共享。为追求高效,文献[7-8]提出了多秘密共享方案。文献[9-10]利用Reed-Solomon译码方案实现对多个秘密的共享;文献[11-12]利用极小授权集合和线性码的对偶码的极小码字之间一一对应的关系构造方案;文献[13]提出了一种基于强单向Hash函数构造出一种可更新、多用途、多秘密共享方案;文献[14]基于线性码的纠错能力构造了一个(l,t+l)门限秘密共享方案,选择线性码中的码字作为秘密,通过线性码译码问题的难度保证了该方案的安全性和可靠性,但是无法保证秘密份额的安全性以及抵抗成员的合谋攻击。
本文在此基础上提出一种新的(n,n)门限多秘密共享方案,以Ham(k,q)的纠错能力为基础,通过将参与者进行分组并建立组员信息,来提高秘密份额的安全性和完成对参与者的更新。利用双变量单向函数的性质,保证秘密的准确性,避免参与者的欺诈行为。本方案具有以下重要特点:① 以Hamming码的多个码字作为方案的多重秘密,利用Hamming码的纠错能力来重构秘密;② 将参与者进行分组,将秘密份额的掌握权限赋予每个组,只有全部n个小组提供其正确秘密份额才能重构秘密,缺一不可;③ 共享多秘密,每个小组的秘密份额可重复使用,用于恢复不同的秘密,具有高效性;④ 抵抗合谋攻击,完成对欺骗行为的识别。本文首先介绍Hamming码和秘密共享方案的一些基础知识,接下来给出算法,进行安全性分析,并通过一个实例来说明该方案。
1 预备知识
1.1 Hamming码
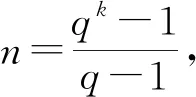
定义1 Ham(k,q)分别从Vα1,Vα2,…,Vαn中任取一个向量作为列向量构成一个k×n阶矩阵H。以H为校验矩阵的线性码称为q元Hamming码,记为Ham(k,q)。
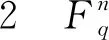
定义3 设C为域Fq上的一个[n,n-k]线性码,对任意的向量a,集合{a}+C={a+x|x∈C}叫做码C的陪集。陪集首是指一个陪集中汉明重量最小的字(陪集首不一定唯一)。
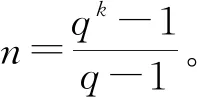
可知Ham(k,q)至多可以纠正一个错误,因此V(n,q)中所有重量不大于1的向量恰好就是Ham(k,q)的标准阵中的所有陪集首。
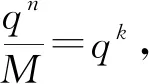
S={(0 …xi… 0)∈V(n,q)|
0≠xi∈GF(q),1≤i≤n}。
设Ham(k,q)的校验矩阵H中的第i列为Hi,1≤i≤n,任取
则
则S中任意2个不同的向量属于Ham(k,q)的不同陪集,又因S中的每个向量不在Ham(k,q)中,且|S|=n(q-1)=qk-1,因此S中的向量是Ham(k,q)的非零陪集的陪集首,即V(n,q)中重量为1的向量都是陪集首。
q元Hamming码Ham(k,q)的译码过程描述如下:
(1)对于在信道接收端收到的向量y,计算校验子S(y)=yHT。
(2)若S(y)=0,则认为没有错误发生,y就是发送的码字。
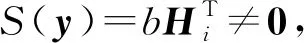
1.2 秘密共享方案
定义4 设s是秘密,n个参与者将秘密s分为v1,v2,…,vn个秘密份额,满足下列条件:①n中任意k个参与者都能重构秘密s;② 任意k-1个或者更少的参与者都无法重构秘密s。
此方案被称为(k,n)门限秘密共享方案[1]。(n,n)门限秘密共享方案是此方案的一个简化门限方案。
定义5 双变量单向函数[16],令f(r,s)表示一个有2个变量的单向函数,它能够将任意长的r和s映射为固定长的函数值f(r,s)。该函数具有以下性质:
(1)已知r和s,f(r,s)易于计算。
(2)已知s和f(r,s),求r在计算上是不可行的。
(3)已知r和f(r,s),求s在计算上是不可行的。
(4)在s未知的情况下,对于任意的r,难以计算f(r,s)。
(5)在已知s的情况下,找到r1≠r2且满足f(r1,s)=f(r2,s)在计算上是不可行的。
2 方案描述
2.1 系统初始化
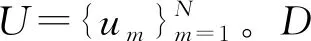
D将H传入公告栏,所有人可查。

2.2 秘密份额分发
D取矩阵E的第t列bt作为秘密份额传给小组Pt,t=1,2,…,n。秘密份额在小组内共享,即同一个小组中的参与者掌握同一秘密份额。计算双变量单向函数f(t,bt)的值,记为f(t)。D将伪秘密份额f(1),f(2),…,f(n)传入公告栏,所有人可查。
2.3 秘密重构
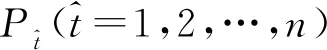
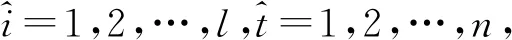

医保办工作人员积极参加医保经办机构组织的各种医保会议及医保管理方法分享等活动,学习最新医保管理策略。邀请上级医保经办机构人员来院进行医保知识讲座和对新政讲解,针对理解不到的内容和案例互动交流,达成对医保政策理解的共识,从而保持医保政策贯彻执行的一致性。
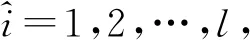
3 安全性分析
3.1 可验证性分析

3.2 安全性
(1)秘密份额的安全性。为了防止每个小组的秘密份额不被泄露,秘密分发者D在构造检验是否存在参与者欺骗行为的公共信息时,传入公告栏的是各组的伪份额f(t,bt),而不应该是各组的真正秘密份额。即使f(t,bt)被泄露,依据双变量单向函数f(r,s)的单向性,难以得到bt,真正的秘密份额则不会泄露。
(2)任何小于n个小组合作都无法得到秘密。假设n-1个小组合作,分别记为P1,P2,…,Pn-1,其秘密份额组成l×(n-1)阶矩阵,即
当i=1,2,…,l时,取得向量vi,其码长为n-1,译码过程无法正常进行。因此,只有全部n个小组提供其正确秘密份额时才能重构秘密。
3.3 动态性
方案具有动态性,能够完成对参与者的更新。若参与者集合U有w个新的参与者uN+1,uN+2,…,uN+w,D将这些参与者分发到M(1≤M≤n)个组,添加成员信息到公告栏。例如,D分发uN+1到P1则uN+1的信息记为(1,uN+1)。小组分享该组秘密份额给新组员,无需重新分发秘密份额。若参与者集合U存在参与者退出,t=1,2,…,n,当|Pt|≠0,删除参与者信息即可;当|Pt|=0,则将所有参与者重新分组,在公告栏中更新新的组内成员信息。
4 实例分析
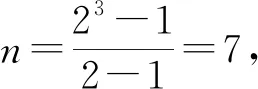

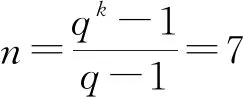
5 结 论
本文讨论了一种新的构造(n,n)门限多秘密共享方案的方法,该方法将Hamming码的不同码字作为多个不同的秘密,根据Hamming码只能纠正一个错误的性质重构秘密,并且可重复使用秘密份额,来恢复不同的秘密;然后依据双变量单向函数的性质,在重构秘密时利用函数验证秘密份额的有效性,能够有效地防止外界敌手和参与者的欺骗行为;最后通过实例来验证该方案的有效性和可行性。

