数形结合 解答数学难题
张仁寿

摘 要: 在数学课程体系中,各个知识点之间相互关联,尤其是在初中阶段,教学内容同小学相比,无论是难度、还是深度均有所提升,相应的试题难度也在一定程度上提升,学生极易遇到难题,教师可指导他们运用数形结合思想来解答这些难题,使其突破解题障碍.
关键词: 数形结合;初中数学;解答难题
中图分类号: G632 文献标识码: A 文章编号: 1008-0333(2021)35-0044-02
数学知识本身就具有典型的抽象性特征,学生学习数学过程中离不开逻辑思维的辅助,在初中数学教学中,面对如此众多的难题,他们容易陷入到困境之中,影响自信心的树立.面对这一现状,初中数学教师可以教导学生运用数形结合思想处理难题,将几何与代数的特点综合在一起,有效降低解题的难度,将解题过程变得通俗易懂,让他们顺利解答难题.以下笔者就如何运用数学结合解答初中数学难题进行探究,并提出几点有效的对策.
一、运用以形助数思想,顺利解答代数难题
在初中数学教学中,很多数量关系都比较抽象,学生难以准确的把握,这时采用以形助数思想是一个不错的選择,就是借助形的几何直观性来阐明数之间某种关系,由此将部分思维具体呈现出来,在解题中起着重要作用.初中数学教师可指引学生运用以形助数思想,把数量关系问题转变成图形问题,实现由抽象向直观的转变,让他们顺利解答代数难题.
例1 已知0解析 这是一道典型的不等式问题,将讲授到不等式知识时,教师可以设置这一难题,本题目的主要难点在于题设中给出的已知信息较少,只是简单的确定a和b的范围,还是以不等式的形式来呈现,而所求证的式子相当长,还涉及到根式、平方式、不等式等相关知识,不仅比较复杂,难度也较大,学生读完题目以后,很难找准突破口,他们将会陷入到困难直送,不知道该如何解题.此时,教师可以引领学生运用数形结合思想中的以数助形思想,将题目中抽象的数量关系以直观的几何图形展示出来,使其形成清晰的解题思路,从而让他们快速求证.具体证明过程如下:
证明:如图1所示,作边长是1的正方形ABCD,在边AB上取点E,设AE=a;在边AD上取点G,使AG=b,过点E和G分别作EF//AD同边CD相交于点F;作G//AB同边BC相交于点,设EF和G相交于点O,把AO、BO、CO、DO、AC、BD分别连接起来.学生根 据题目中的条件与要求画出下面的图形以后,能够判断出三角形AOG、三角形BOE、三角形COF和三角形DOG都直角是直角三角形,所以根据勾股定理能够得出OA= a2+b2 , OB= (1-a)2+b2 ,OC= (1-a)2+(1-b)2 ,OD= a2+(1-b)2 ,且AC=BD= 2 ,因为OA+OC≥AC,OB+OD≥BD,所以能够得出 a2+b2 + (1-a)2+b2 + a2+(1-b)2 + (1-a)2+(1-b)2 ≥2 2 ,但是当且仅当a=b= 1 2 时等号才成立,即为此时该式子的值是2 2 .
对于这道初中数学难题,对于广大初中生来说一般都无法轻松求证,主要原因在于虽然从表面上看是一个不等式,但是实质上涉及到知识点众多,处理起来还比较复杂,不过教师可以指引学生在求证这类条件不等式题目时,可根据题设条件作出对应的图形,然后让他们运用图形的几何性质或者平面几何的定理、公理去建立不等式,最终使结论获得证明.
二、采用以数助形思想,有效解答几何难题
就数学知识来说,形具有显著的优势,能形象、直观的呈现信息,无论什么事物,均具有正反两面性,形不足之处就是很难做到十分精准,有些图形较简单,通过直接观察难以得出规律,这就要基于代数视角来分析和计算.初中数学教师可根据实际题目引导学生采用以数助形思想,使其借助于数的精确性来阐明形的某些属性,让他们有效解答几何难题.
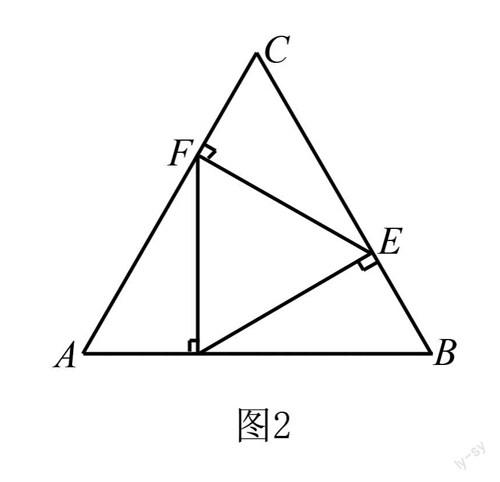
例2 如图2所示,在正三角形ABC中,AB、BC、CA三条边上分别有点D、E、F,如果DE垂直于BC,EF垂直于AC,FD垂直于AB同时成立,求点D在边AB上的位置.
具体解题方法如下:先假设题干中符合条件的点D、E、F均已经作出,再结合给出的已知条件,寻求三角形中线段和角之间的数量关系,然后采用代数中的方程知识列出含有未知数的等式,以此求解.
解:设边AB的长度是1,AD的长度是x,由于△ABC是一个正三角形,且DE⊥BC,EF⊥AC,FD⊥AB,所以得到BD=2BE=8x-2,即得出方程x+(8x-2)=1,解之得x= 1 3 ,又因为AD+BD=1,AF=2x,CE=1-2x,CD=2CF=2-4x,BE=1-CE=4x-1,由此说明点D的位置是位于边AB上的 1 3 分点处.
其实在初中数学几何教学中,通常存在着这样一类问题,即为几何图形中的某些点的位置或者线段的长度或者角度的大小无法根据题意直观明了的画出来,只有根据已知条件求出某一些量时,图形才能够画出,而求那些量的方法,教师可指导学生通过列方程或者方程组进行求解,就是将几何问题转化成代数方程计算,让他们借助数学结合思想解答这类难题.
三、注重数形相互转化,高效解答数学难题
数与形是数学中最基本和最古老的两个研究对象,它们在一定条件下能相互转化.不少初中数学题目并非纯粹的以数变形或以形变数,而是需将两者相互转换,这就要求学生不能只思考从直观的形转换成严密的数,也不能只从严密的数描述直观的形,而是以题目中固有的条件与结论为着手点,科学分析与发现数与形的相互转化关系,高效解答数学难题.
例3 在数学拓展活动中,某兴趣小组为求出 1 2 + 1 4 + 1 8 +……+ 1 2n 的值,先设计出边长是1的正方形纸,而且通过各种标记把正方形面积的 1 2 , 1 4 , 1 8 ……清楚地标注出来,要求你结合已经掌握的数形结合思想推理出假如n是正整数,求出 1 2 + 1 4 + 1 8 +……+ 1 2n 的最终结果,其中可以用n来表示.
具体来说,解题流程如下:学生可以从这个角度展开理解,准备一个边长是1是正方形,使用剪刀把该正方形纸片剪下来,第一次剪掉这张纸片的一半,那么剩余正方形的面积就是 1 2 ,第二次再将剩下正方形纸片的一半剪下来,得到的图像面积就是原正方形纸片面积的 1 4 ,第三次把上次剩下的图形继续剪掉一半,得出的图形即为原正方形纸片面积的 1 8 ,以此类推,也就是每次都把上次裁剪剩余图形面积的一半剪掉,这样在进行第n次裁剪以后,获取到的图形的面积就是( 1 2 )n.之后,学生把所有裁剪下来的图形的面积相加,能够求出 1 2 + 1 4 + 1 8 +……+ 1 2n 的最终结果是1- 1 2n ,由此计算出该式子的答案.
如此,教师利用这样一道典型的数学题目展开解题训练,学生在解题过程中应用数形结合思想时,不仅要用到“以数解形”,还要用到“以形助数”,将 “数”与“形”信息进行灵活自如的转换,由此实现对数形结合思想的巧妙应用,同时训练他们的数学思维品质,将复杂数学难题变得简单化,使其形成最优解题思路,最终快速、准确的计算出答案.
参考文献:
[1]谢立影.浅析初中数学教学中数形结合方法的具 体应用策略[J].天天爱科学(教育前沿),2021(09):69-70.
[2] 刘洪燕.初中数学教学中数形结合思想应用能力培养探讨[J].中学课程辅导(教师通讯),2021(16):100-101.
[3]徐晓霞,王洪英.数形结合思想在初中数学解题中的应用[J].现代中学生(初中版),2021(Z4):66-67.
[4]李三平.初中数学教学中学生数学解题能力的培养[J].数理化解题研究,2021(17):24-25.
[责任编辑:李 璟]

