C*代数值度量空间上的第一类扩张映象及不动点定理

麻振华 郑世良 邓全才 王占伟

(河北建筑工程学院数理系，张家口 075000；张家口市经开区第一小学，张家口 075000)

1 引言与基本概念

麻振华等人在2014年次提出C*代数值度量空间的概念[1]，并研究了相关不动点定理.随后几年，国内外诸多学者研究了该空间上的不动点定理并得到了许多重要结果[2,3,4].以文献[1]和[5]为基础，本文给出了该度量空间上一类扩张映象的定义，同时给出了一个相应得不动点定理，此定理推广了一般度量空间的相关结论．

我们先回顾与本文有关的概念：

定义1.1[9]如果集合A满足以下关系：

(1)a≼a;

(2)a≼b,b≼a⟹a=b;

(3)a≼b,b≼c⟹a≼c,

则在集合A上定义的二元关系≼称为集合A上的偏序。

注：一个包含偏序的非空集称为一个偏序集合，简称为偏序集，在偏序集A中我们用ab表示a≼b且a≠b.

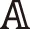
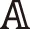
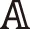
(1)0≼d(x,y),∀x,y∈X且d(x,y)=0⟺x=y(非负性)；

(2)d(x,y)=d(y,x),∀x,y∈X(对称性);

(3)d(x,y)≼d(x,z)+d(z,y),∀x,y,z∈X(三角不等式)，

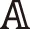
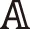
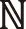
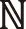
注：方便起见，以下我们用θ表示0.

2 主要结果

我们先给出C*-代数值度量空间中第一类扩张型映象的定义如下：

定义2.1设(X,A,d)是完备的C*代数值度量空间，映射T∶X→X满足以下条件：存在正整数p,q和A∈A可逆，且‖A-1‖<1，使得

d(Tpx,Tqy)A*d(x,y)A，对任意x,y∈X的成立，

则称T是C*-代数值度量值第(1)类扩张型映象.

定理2.1设T∶X→X是C*-代数值度量空间第第一类扩张型映象，且是满射，则T在X中具有唯一不动点.

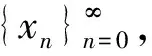
y0=x0,y1=xq,y2=xp+q,…，

y2n-1=x(n-1)(p+q)+q,y2n=xn(p+q),n=1,2,…，

于是有

y2n-1=TPy2n,y2n=Tqy2n+1,n=1,2,….

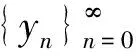
事实上，由于d(y2n-1,y2n)=d(TPy2n,Tqy2n+1)A*d(y2n,y2n+1)A可知，

d(y2n,y2n+1)≼(A*)-1d(y2n-1,y2n)A-1.

同理，

d(y2n-1,y2n)≼(A*)-1d(y2n-2,y2n-1)A-1.

结合上面二式，对任意n=1,2,…，可得

d(yn,yn+1)≼(A*)-1d(yn-1,yn)A-1≼…≼[(A*)-1]nd(y0,y1)(A-1)n.

所以，可得

‖d(yn,ym+n)‖≤‖d(yn,yn+1)+d(yn+1,yn+2)+…+d(ym+n-1,ym+n)‖

≤‖[(A*)-1]nd(y0,y1)(A-1)n+[(A*)-1]n+1d(y0,y1)(A-1)n+1+…

+[(A*)-1]m+n-1d(y0,y1)(A-1)m+n-1‖

≤‖[(A*)-1]nd(y0,y1)(A-1)n‖+‖[(A*)-1]n+1d(y0,y1)(A-1)n+1‖+…

+‖[(A*)-1]m+n-1d(y0,y1)(A-1)m+n-1‖

≤‖[(A*)-1]n‖‖d(y0,y1)‖‖(A-1)n‖+‖[(A*)-1]n+1‖‖d(y0,y1)‖‖(A-1)n+1‖

+…+‖[(A*)-1]m+n-1‖‖d(y0,y1)‖‖(A-1)m+n-1‖

≤‖[(A*)-1]‖n‖d(y0,y1)‖‖A-1‖n+‖[(A*)-1]‖n+1‖d(y0,y1)‖‖A-1‖n+1+…

+‖[(A*)-1]‖m+n-1‖d(y0,y1)‖‖A-1‖m+n-1

=‖d(y0,y1)‖‖(A*)-1]‖n‖[A-1‖n(1+‖[(A*)-1]‖‖A-1‖

+‖[(A*)-1]‖m-1‖A-1‖m-1)

因‖A-1‖<1，故‖(A*)-1‖<1.

因此，

两边取对数，有

nln‖[(A*)-1]‖‖A-1‖≤ln(1-‖[(A*)-1]‖‖A-1‖)ε-ln‖d(y0,y1)‖

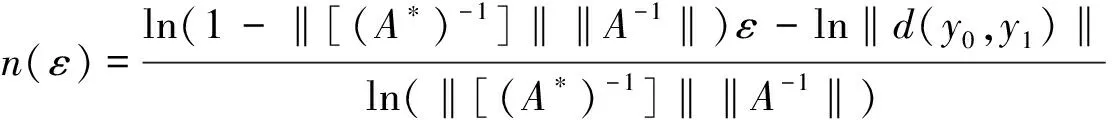
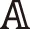
d(z,y2n)=d(TP(u),Tqy2n+1)A*d(u,y2n+1)A

上式两端n→∞，得θA*d(u,z)A，故u=z，即z=TP(z)，因而z是TP的不动点.

下证唯一性：

如果还存在另一点w∈X是Tq的不动点，则有

d(z,w)=d(TPz,Tqw)A*d(z,w)A

上式成立当且仅当z=w，故z是Tp和Tq的唯一公共不动点，另外，显然有

Tz=Tp(Tz),Tz=Tq(Tz)，

故由z的唯一性得知z=Tz.

证毕.

3 结 论

本文主要是在C*-代数值度量空间基础上给出了C*-代数值度量空间上第(1)类扩张映象的定义，并证明了其不动点的存在和唯一性.该定理推广了一般度量空间上的第(1)类扩张映象不动点定理.