以地热能为热源温室大棚土壤温度场的研究

贾玉贵 宋 涛*

(1.河北省可再生能源供热工程研究中心，河北 张家口 075000;2.河北建筑工程学院，河北 张家口 075000)

0 引 言

“30碳达峰，60碳中和”开启了可再生能源时代的大幕.大力推动新时代可再生能源大规模、高比例、高质量、市场化发展，有力推动可再生能源从能源绿色低碳转型的生力军成长为碳达峰碳中和的主力军，为构建清洁低碳、安全高效的能源体系提供坚强保障.地热能作为可再生能源的代表，具有清洁、环保、高效、丰富、低温的优点，是温室大棚热源的优先选择目标.

1 室内环境下(15 ℃)土壤初始温度曲线

当温室大棚室内环境温度为15 ℃时，土壤初始温度为8 ℃时.假设土壤为各向同性的固体，物性参数为常数.忽略由于土壤中水分迁移而引起的热迁移.已知土壤导热系数为2.04 W/(m·℃)，密度为2400 kg/m3，比热容为921.1 J/(kg·℃)，在此条件下模拟土壤不同深度下的温度值，从而得到土壤表面不同深度下土壤温度曲线图.

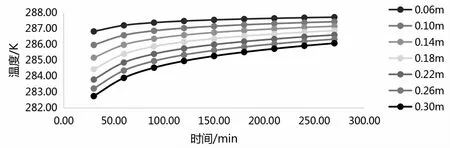
图1 土壤表面不同深度下土壤温度曲线图

图1为土壤温度随着时间积累各不同深度监测点的温度曲线图，室内环境温度为植物适宜的环境温度15 ℃，监测点距离土壤上表面的垂直距离分别为0.06 m、0.10 m、0.14 m、0.18 m、0.22 m、0.26 m、0.30 m，每相邻两监测点相差4厘米.从图中我们可以看出：土壤温度变化速度与范围随着监测点深度和时间的变化而变化.

整体上来看，土壤监测点内的温度具有升高的趋势，距离地表最近的温度变化较小.随着深度的增加土壤温度升温较快.随着时间的增加，土壤的温度逐渐趋于稳定.这说明，随着时间的增加，土壤温度在一定范围内有着提高，表面温度的影响也随之下降.为了节能，室内温度选择植物适宜的15 ℃时，土壤温度达不到适宜温度，在实际项目中有必要用地埋管来提高土壤的温度.

2 日光温室地下土壤的传热学的机理

(1)土壤表层与室内空气的对流换热：

q1=hs(tm-tf)

(1)

式中：

q1——土壤表层与温室空气的热流密度，W/m2；

hs——温室地表层的对流换热系数，W/(m2·K)；

tm——温室地表层的平均温度，℃；

tf——温室内环境温度，℃.

(2)管内热水与管壁热流密度为：

q2=hg(tg-t0)

(2)

式中：

q2——管内热水与管壁的热流密度，W/m2；

hg——管内对流换热系数，W/(m2·K)；

tg——散热管水的温度，℃；

t0——温室地下土壤温度，℃.

(3)管壁与土壤的导热：

由于沿管长方向的温度变化很小，所以土壤内部导热可以看作是二维非稳态导热，控制方程为[1]：

(3)

式中：

t——土壤温度场中的温度值，℃；

α——土壤的热扩散率，m2/s.

3 温室大棚土壤温度场模型建立

3.1 模型假设条件

(1)忽略温室内部的温度差异，将温室内部温度看作一致.

(2)土壤、地埋管为各向同性的固体，物性参数为常数.

(3)忽略沿管长方向的传热，将地埋管周围土壤温度场作为二维瞬态导热问题处理.

(4)忽略土壤内水分迁移引起的热迁移.

(5)由于地埋管管壁很薄，认为管壁与土壤导热系数相同.

3.2 土壤温度场控制方程及边界条件

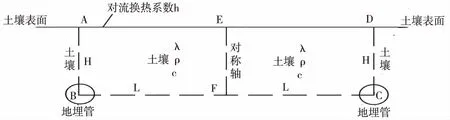
图2 土壤温度场数学模型

土壤二维非稳态导热控制方程：

(4)

边界条件：(1)土壤上表面与温室大棚内的空气存在对流换热，为第三类边界条件：

(5)

(2)由于温室地埋管对称布置，所以两侧没有热量的传递，视为绝热面，为第二类边界条件：

(6)

(3)温室大棚土壤底部较为稳定，把底部视为恒温面，为第一类边界条件：

t=t0

(7)

土壤温度场二维非稳态导热微分方程通过对非齐次边界条件齐次化，分离变量[2-3]，得：

θ(x,y,t)=V(x,y,t)+W(x,y)

(8)

代入上壤的导热系数、热扩散系数和管道埋设深度和管间距等相关数据,可得温室地下土壤温度的二维分布情况[4].

4 模型建立与参数设置

将温室大棚土壤的计算模型假定为一个1×1(m)的计算模拟区域，地埋管位于模型中的坐标为(0.5，0.5)米.将计算区域网格用网格划分软件Gambit划分.划分完成后检查其准确性.然后将模型导入Fluent软件进行参数的设置，开始对模型进行模拟.网格划分如下：

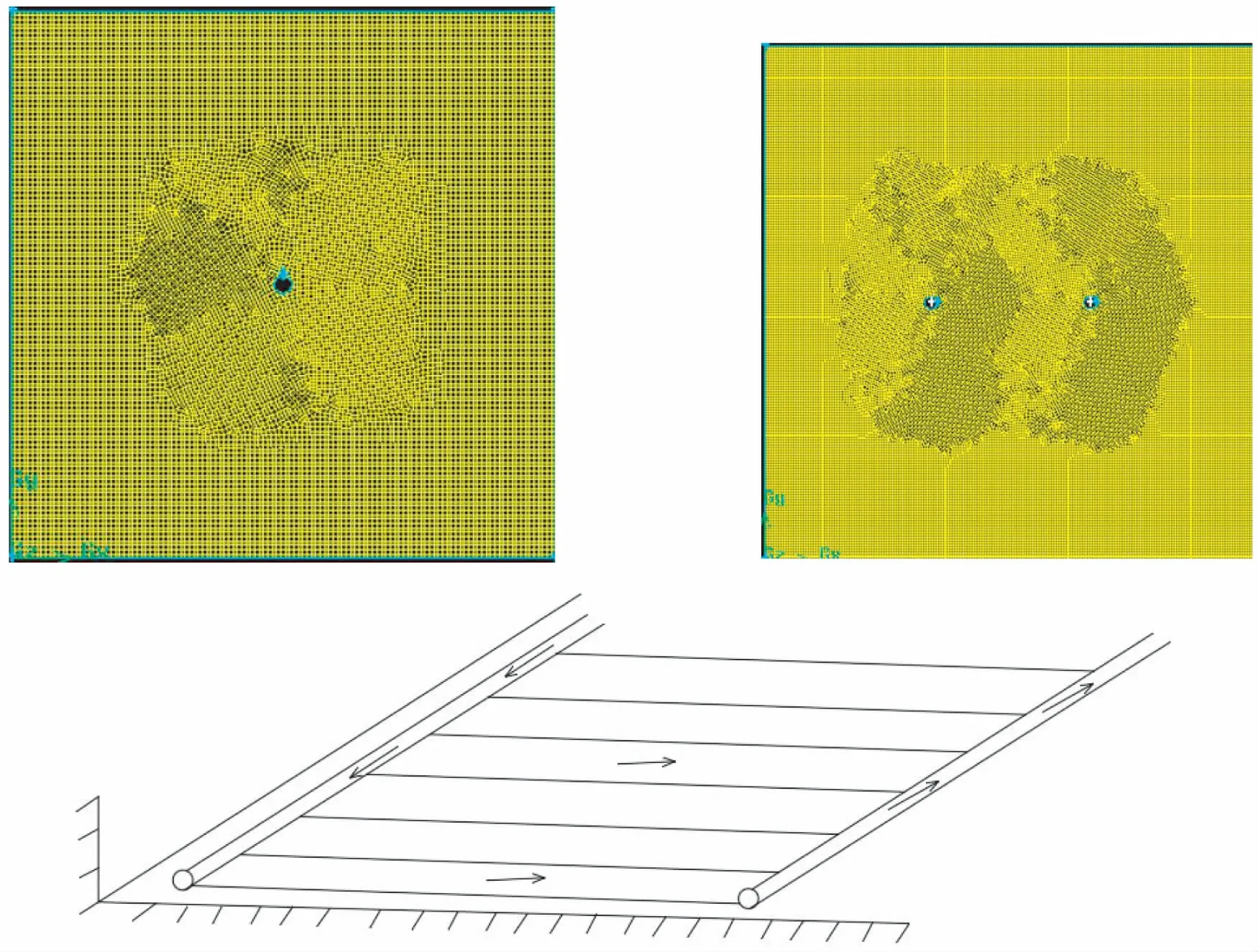
图3 地埋管布置示意图

初始条件和边界条件

1)土壤：土壤导热系数为2.04 W/(m·℃)，密度为2400 kg/m3，比热容为921.1 J/(kg·℃);

2)聚乙烯管(pe)导热系数为0.4 W/(m·℃),密度为933 kg/m3；

3)供水平均温度：50 ℃；

4)冬季土壤区域初始温度为8 ℃，温室地表环境温度为15 ℃，地表与空气对流换热系数为7 W/m2.

5 模拟结果与分析

5.1 同一管径不同时间下的土壤温度场分析

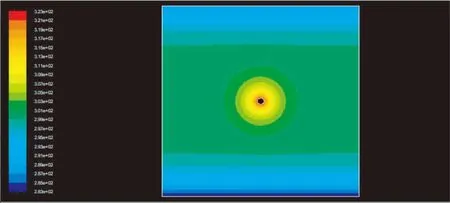
图4 管径32 mm,120 min后的温度分布

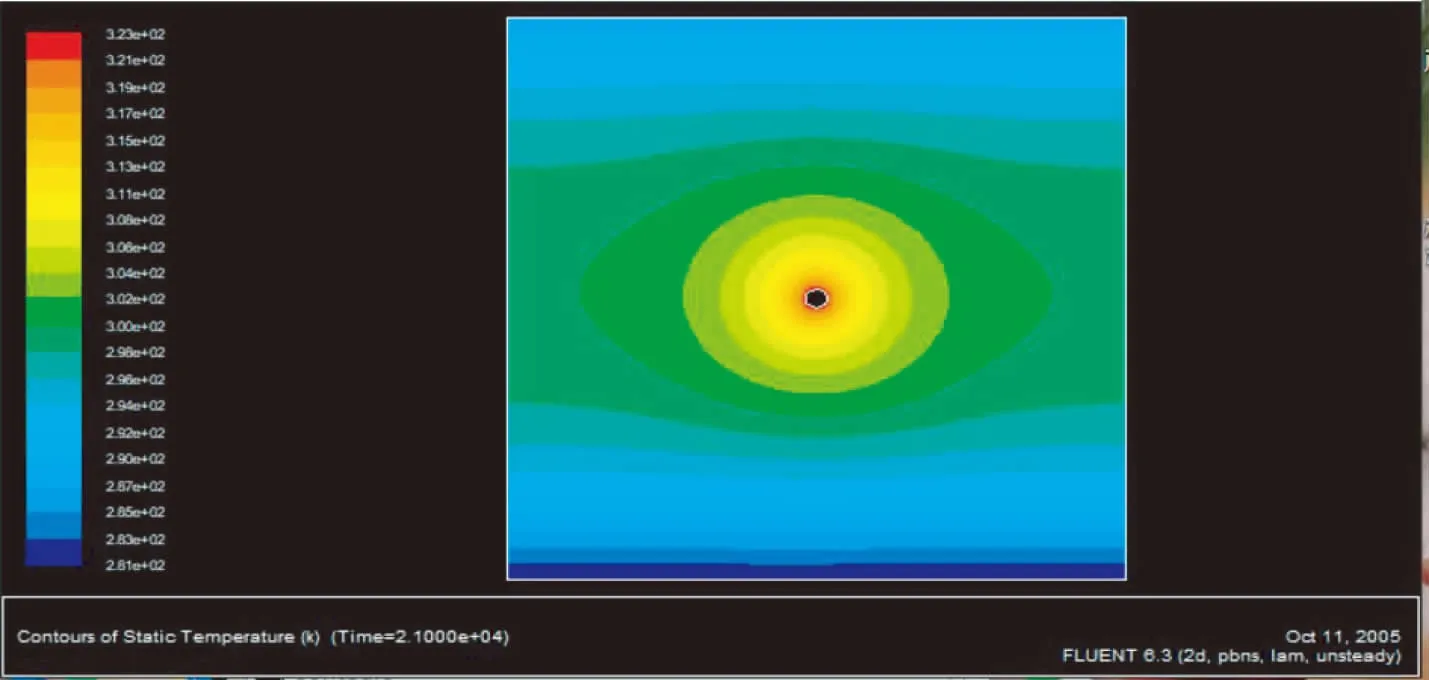
图5 管径32 mm,350 min后的温度分布

如上图4，图5.管径32 mm的地埋管在地源热泵加热运行120 min，350 min后土壤温度场的云图可以看出，土壤的温度分布是以地埋管为中心向外扩散，靠近地埋管周围温度较高，四周温度逐渐降低.随着加热时间变化，经计算，同一监测点温度提高,这说明，随着加热时间推移，地埋管传递的热量逐渐向土壤深层转移.温室地埋管的热作用半径在随着时间的增加进一步的增大.从模拟结果的温度云图还可以知道，随着热作用半径的增加，温度在逐渐的降低.

5.2 不同管径不同时间下土壤温度场分析

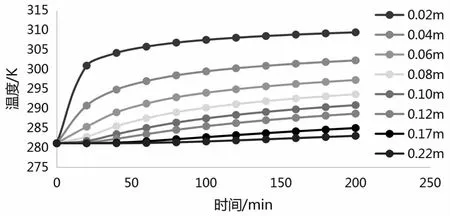
图6 距地埋管(32 mm)不同深度下土壤各点温度曲线图

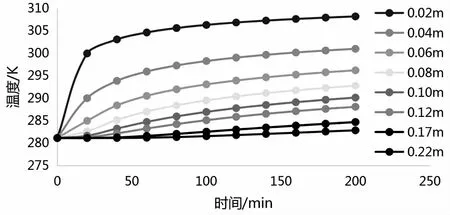
图7 距地埋管(25 mm)不同深度下土壤各点温度曲线图

图8 距地埋管(16 mm)不同深度下土壤各点温度曲线图

图6,图7，图8为距离地埋管不同距离的土壤温度曲线图.各个监测点距离地埋管的垂直距离分别为0.02 m、0.04 m、0.06 m、0.08 m、0.10 m、0.17 m、0.22 m，从图中我们可以看出：在地埋管加热运行的情况下，土壤温度整体上呈现了上升的趋势，靠近地埋管壁面处温度变化率较大，土壤升温较快，在监测点范围内，0-120 min土壤温度变化较大，之后温升变慢.管径分别为16 mm,25 mm,32 mm的地埋管在同一监测点(0.06 m)，同一时间(100 min)下土壤温度依次为291.678 K、293.089 K、293.999 K.这说明随着管径的增加土壤的温升越快，热作用半径越大.随着距离地埋管距离的增加，土壤温度达到平衡的时间也增加.

5.3 不同管径下的土壤温度场分析

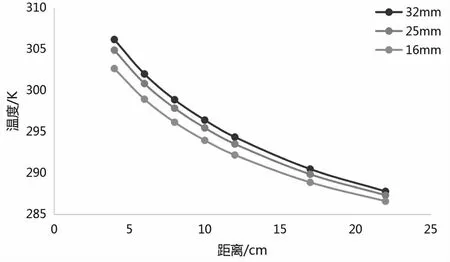
图9 不同管径下土壤的温度曲线图

图9为系统加热12 h后距离监测点不同距离下的土壤温度曲线图.从图中看出当当管径为16 mm时，土壤的温度场影响范围为5.1 cm-17.8 cm；当管径为25 mm时，土壤的温度场影响范围为6 cm-19.3 cm；管径为32 mm时，土壤的温度场影响范围为6.8 cm-20.4 cm.随着管径的增加热作用半径随之增加，但是热作用半径增加范围有限，管径从16 mm到25 mm热半径扩大了4.5%，管径从25 mm到32 mm热半径扩大了2.2%，价格分别增长了21.7%，27.3%.热作用半径增加有限，价格增幅较大.

图10 不同管间距下土壤的温度曲线图

图10为系统加热12 h后距离监测点不同距离下的土壤温度曲线图.由图可以看出，不同管径不同间距下的土壤温度不同管径不同间距下土壤温度场是不一样的，间距偏小会导致热量的堆积，从而导致供热热量的的增加，管材使用的量增加；间距偏大导致管中心位置的土温因管道散热量的不足而不能满足所需温度.管径为16 mm时，热作用半径为5.9-20.1厘米，管径为25 mm时，热作用半径为7.1-23.7厘米，管径为32 mm时，热作用半径为7.9-24.3厘米.相比较单管的热作用半径提高了1.3厘米，3.3厘米，3.8厘米.

5.4 不同管间距下土壤温度场的分析

由5.3可知，当管径为25 mm时，热作用半径以及经济性都能达到较为理想和节约的目标.为了确定管间距，分别对管间距为0.2 m,0.25 m,0.3 m下的土壤温度值进行数据的采集.

表1 管径为25 mm时，在不同地埋管间距下具有不同的温度值

当管径为25 mm时，在不同地埋管间距下具有不同的温度值.横坐标值为0.3 m为埋管正上方的温度值.横坐标值为为0.4 m、0.425 m、0.45 m分别为两地埋管中心上方的温度值.当间距为20 cm、25 cm时，在距离地埋管不同深度下都会出现热量的堆积现象，这样会造成供热量的增加不利于节能运行.当间距为30 cm时，同一深度下的个监测点温度基本相同，没有温度差.有利于节能运行.

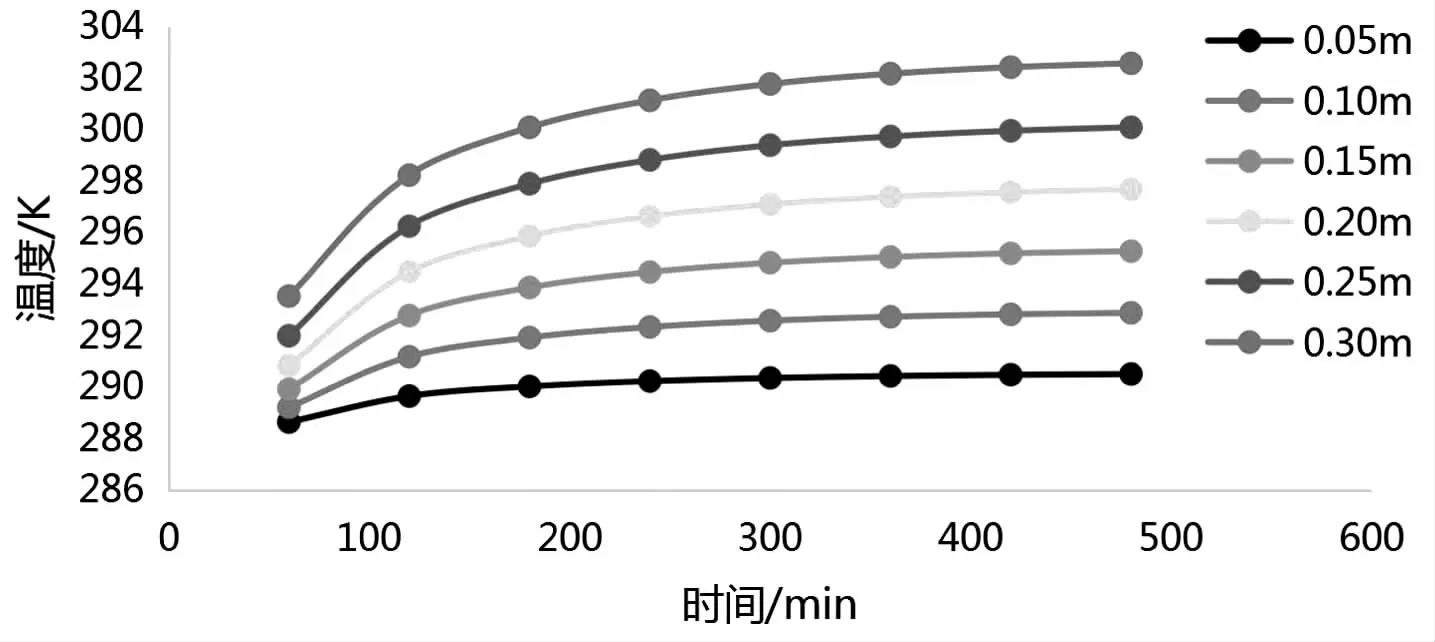
图11 不同温室土壤尺寸温度分布

上图为在地源热泵提供热水平均温度50 ℃时，当管径为25 mm，间距30 cm，埋深在57.7 cm时温室土壤5-25厘米(根系一般为5-25 cm)的温度值.从图中我们可以知道，温室土壤5-25厘米最高温度为26.94 ℃，最低温度为17.36 ℃均能够满足种植物的根温要求(15-30 ℃).

6 结 论

(1)影响温室大棚土壤温度场的因素有地埋管的管径，间距以及埋深.地埋管管径越大，影响到的土壤的温度范围就越广，热作用半径越大；当管径相同时，间距越大导致土壤温度场不均匀分布；埋深直接影响植物根系温度.

(2)当假设土壤物性均匀不变的前提下，忽略地埋管沿管程方向的温变以及管壁的导热时，通过利用Gambit建立温室土壤的二维模型，并导入FLUENT进行数值模拟计算，对模拟结果从节能和经济效益考虑，在地源热泵提供热水平均温度50 ℃时，当管径为25 mm，间距30 cm，埋深在57.7 cm时温室土壤温度场为最佳，此时温室土壤5-25厘米平均温度为22.14 ℃.