考虑风电相关系数矩阵非正定的概率潮流计算

胡建军，郭 飞*，王 波，吴佳静

(1.国网宁夏电力有限公司，银川 750001；2.国网宁夏电力有限公司吴忠供电公司，吴忠 751100；3.宁夏信通网络科技有限公司，银川 750001)

随着全球能源资源配置的逐步调整，化石能源和可再生能源供应成本总体呈现出“一升一降”的趋势[1-2]，风电技术的发展和突破使其在可再生能源中所占比重逐渐加大，未来电力系统新场景已全面开启[3]。但风能具有强波动性和间歇性，并网后使得系统的源端呈现强随机性，给系统运行稳定性带来严峻挑战。

概率潮流(probabilistic power flow，PPF)可考虑系统随机信息，研究成果可分为模拟法(monte carlo simulation，MCS)、解析法和点估计法三类[4]。模拟法不受系统规模和非线性的约束，计算精度高，但比较耗时。拉丁超立方(Latin hypercube sampling，LHS)作为一种改进方法，通过分层抽样改善了随机变量在空间中的覆盖程度，采样效率提高显著[5]。解析法常用半不变量法，突出特点是计算速度快，但其需要对潮流方程线性化处理，因而当输入随机变量波动范围较大时，计算结果误差较大。点估计法根据输入随机变量的前几阶矩信息，得到输出随机变量的均值和方差，但无法描述整体概率特性。

描述风电功率随机波动特性的概率模型已有广泛研究，文献[6-7]采用Weibull分布和常规正态分布分别拟合风电出力和负荷概率模型，其理论上具有普适性，但无法正确捕捉变量多峰性和强随机性。文献[8]采用高斯混合模型(Gaussian mixture model，GMM)刻画负荷随机性，并通过历史数据验证了该模型的准确性。文献[9]探究了采用GMM不同维数情形下拟合风电场和集群风电场的可行性。事实上，GMM可以更加准确地描述变量强随机波动，其拟合曲线可呈现不对称、多峰分布的概率特性。

在构建变量的概率模型基础上，如何有效解决计及新能源出力强随机性的 PPF 是现有潮流计算研究的难点。现有PPF方法难以计及状态变量的先验信息和当前观测数据的内在联系，贝叶斯理论将状态变量视为变动的参数，随着观测数据的不断累积而改变[10]。近似贝叶斯计算(approximate Bayesian computation，ABC)方法通过对比模拟数据集和观测数据集来估计变量后验概率[11]，可用作解决电力系统似然函数未知的问题。此外，已有研究中处理随机变量相关性较广的方法包括Cholesky分解、随机排序等[12-13]。但在实际应用中，描述随机变量两两之间关系的相关系数通常是非理想条件的，采用奇异值分解的方法得到考虑相关性的状态变量样本，可灵活处理相关系数矩阵非正定的情形。

基于上述分析，现提出一种基于序贯重要性采样(sequential importance sampling，SIS)改进ABC的方法解决PPF问题。首先采用GMM建立风电出力不确定模型，利用奇异值分解结合Nataf变换灵活处理相关系数矩阵非正定的情形。其次，将具有先验信息的状态变量转化为模拟数据集，通过ABC对比观测数据集以获取后验估计。最后，采用样本加权方式和扰动核来避免出现低接受率情况，通过算例仿真证明所提方法的高精度和高效性。

1 随机潮流不确定模型

1.1 风电场概率模型建立

风电场并网概率模型的建立方法主要分为参数方法和非参数方法两种。文献[14]采用GMM建立风电出力不确定模型，该模型概念上简单易懂，融合了参数模型和非参数模型各自的优势，可以灵活高效地考虑多维随机变量之间的相关性变化。采用混合高斯分布表示风电场出力的概率函数fGMM(x)为

(1)

(2)

文献[9]验证了二维GMM可有效表示风电场出力。因此用二分量GMM表示风电场有功出力的概率分布为

(3)

式(3)中：α为权重。

采用最大期望(EM)算法求解GMM中未知参数值，其分作两步迭代更新隐藏变量和模型分布参数，最终收敛后，保证得到全局最大值。从而降低计算最大似然估计的难度。

给定风电场出力数据X={x1,x2,…，xN}，GMM的似然函数为

(4)

式(4)中：Θ=(θ1,θ2,…,θN)。对式(4)取对数得

(5)

使用EM算法求解风电场出力概率函数中未知参数结果为

(6)

式(6)中：m为求解最大化对数似然函数次数；n为参数变量个数；p为参数的迭代次数；Gm为后验密度函数。

1.2 线性化交流潮流模型

交流潮流方程一般可表示为

(7)

式(7)中：W为节点注入功率，即输入随机变量，包括负荷、风电节点注入功率；Z为支路潮流，即输出随机变量；x为系统的状态变量，包括电压幅值和相角。

概率潮流的目的是根据节点注入功率W的概率分布，通过W与状态变量x的线性化关系g，得到x的数字特征，进而求得支路有功、无功功率的数学特征。

2 考虑相关随机变量概率潮流计算

2.1 输入变量相关性控制

评估新能源并网对系统运行的影响，应同时考虑出力的强随机性和相关性。具有相关性的随机功率注入对系统产生潮流扰动，常用随机排序、Cholesky分解和遗传算法的处理方法来获得具有相关性的样本序列。为了可灵活处理相关系数矩阵非正定的情况，在此采用奇异值分解结合Nataf变换的方法处理多维输入随机变量。假定存在n维输入变量X=[X1,X2,…,Xn]T，其相关系数矩阵ρX=(ρXij)n×n，累积分布函数Fi(Xi)。通过式(8)等概率变换为标准正态随机变量Z=[Z1,Z2,…,Zn]T。

(8)

式(8)中：Φ(·)和Φ-1(·)分别为Zi的累积分布函数及其反函数；Fi(Xi)和Φ(Zi)服从U[0,1]。

变换后ρZ=(ρZij)n×nρX和ρX的非对角元素由式(9)得出，即

ρZij=T(ρXij)ρXij

(9)

式(9)中：T(ρXij)为ρXij和ρZij之间的转换系数，该表达式与Xi、Xj的概率分布有关。文献[15]给出了已知ρXij时，如何快速求得ρZij的方法。

上述过程完成后，需再次变换到独立标准的正态空间。将ρZ进行奇异值分解，可处理非正定或非满秩矩阵等情况。对于任意矩阵Am×n，都存在式(10)分解：

(10)

式(10)中：Σ为由Am×n奇异值构成的对角阵，对角元素降序排列；Um×n为列正交矩阵；Vn×n为正交阵。当m=n时，U=V。

奇异值分解具有以下性质，假设H为n维独立标准正态分布向量，对ρZ进行奇异值分解生成矩阵L为

(11)

式(11)中：UρZ为酉矩阵；ΣρZ为由矩阵奇异值组成的对角阵，对角元素按大小排列；则式(12)定义相关系数矩阵Z*为

(12)

2.2 ABC序贯蒙特卡洛算法

2.2.1 ABC简介

ABC的基本理念是在已知输入随机变量先验概率分布的基础上，利用贝叶斯定理匹配观测数据，从而快速得到输出变量的概率特性。传统贝叶斯公式为

(13)

式(13)中：P(θ|Y)为参数θ基于样本Y的后验分布；f(Y|θ)为条件概率，即似然函数；P(θ)为基于已知经验提供的θ的先验概率分布；f(Y)为总条件概率，常归一化为常值。

在无法获取似然函数的条件下，ABC的思想是先确立θ的先验概率分布P(θ)，用式(14)来估计后验分布。

P[d(Y,Y′)≤ε]P(θ)

(14)

式(14)中：条件分布Pε(Y|Y′)用作衡量样本差距；P(Y′|θ)为由概率模型生成的模拟量；误差函数d(Y,Y′)和阈值ε用于判断采样点是否符合观测值。

通过这一过程，θ先验分布的采样点通过观测值Y的作用下转化为后验分布。具体是，从先验分布P(θ)中随机采样得到θ*，从而构成模拟数据集Y′，考虑到计算效率，通常不应采取完整数据集进行比较，而是选取适当的概要统计量来替代完整数据集，通过概要统计量S(Y)、S(Y′)比较模拟数据集与观测数据集，计算d[S(Y),S(Y′)]≤ε的结果，则可以判断是否将θ*作为参数的后验概率估计值。

然而，ABC算法具有接受率低的不足，主要有以下两类原因，一是当先验、后验分布概率特征差异较大时，无信息性的先验样本会降低接受率；二是阈值ε的选取会产生不同的后验估计结果。这将ABC局限在原始数据集是低维、离散的情况，对于高维、连续的原始数据集，往往很难应用。

2.2.2 基于SIS改进ABC

(15)

以上方法在此记为ASMC，具体步骤如下：

(2)前一代粒子集θi以权重wi抽取一个样本θ*后，通过扰动核得到θ**=q(θ**|θ*)。

(3)将θ**代入P(θ)，P(θ**)=0成立则代入实际模型计算模拟数据集Y′，否则回到步骤(2)。

(4)判断d[S(Y),S(Y′)]≤ε,成立则保留该样本θ**，否则回到步骤(2)。

(6)回到步骤(1)，令t=t+1，直到迭代次数达到T，得到最终样本序列θT。

2.3 基于ASMC的概率潮流计算流程

将本文ASMC方法结合奇异值分解的Nataf变换用于风电并网系统概率潮流计算当中，流程如图1所示，具体如下。

图1 PPF计算流程图Fig.1 Flow chart of PPF calculation

(2)观测数据集生成。对于系统中存在的n个状态变量(电压和相角)，设定先验分布P(θn)，基于1.2节建立实际模型g(·|θn)，根据2.1节生成具有相关性的随机变量观测的样本数据集Y。

(3)ASMC模型生成。建立误差函数d[S(Y),S(Y′)]，扰动核q(·|θ*)，概要统计量S(·)，阈值ε={ε1,ε2,…,εT}。根据2.2.2节完成模拟数据集Y′和观测数据集Y的差异程度对比。

(4)概率潮流计算。将得到的各组状态变量样本集代入潮流计算式中，利用概率统计方法得到输出变量的数学特征。

3 算例分析

3.1 算例介绍

在改造的IEEE-30节点系统中进行仿真测试，系统结构如图2所示。

图2 改造的IEEE-30系统结构图Fig.2 System structure of modified IEEE-30

在节点17、节点19、节点21、节点24接入 30 MW 的风电场，新能源渗透率水平约为20%，恒定节点功率因数0.9。此外，假定系统中的负荷均服从正态分布，以标准系统中给定的负荷值作为期望值，取标准差为期望值的10%。假设风功率相关系数矩阵为非正定阵，表示为

(16)

以下采用本文方法进行潮流计算，由于ASMC是通过对粒子集赋予相应权重，再经过阈值迭代后，使样本逐步符合真实后验概率分布，先验分布的选取不再是影响样本接受率的重要指标。在此根据历史经验对状态变量先验分布进行假设，假定系统中的电压服从N(1,0.12)，相角服从N(μθ,0.12)，采用传统直流潮流算法解出μθ。选择正态分布η～N(0,σ2)作为扰动核q(·|θ*)，叠加η作为样本点的偏移，将上一代形成的样本集方差作为σ。为避免选择阈值ε的主观性对后验概率估计精度造成影响，取ε={ε1,ε2,…,εT}，根据迭代次数其取值逐渐减小。距离函数采用经典的均方根误差作为判定公式，即

(17)

式(17)中：XY,m和XY′,m分别为第m个观测数据集Y和模拟数据集Y′计算得到的概要统计量。

3.2 风电出力概率拟合

从德国某电力公司获取的风电出力数据，将其作为观测数据代入EM算法计算公式中，求解出GMM中的未知参数。表1给出了采用二维 GMM 拟合实际风功率得到的各子成分参数。图3比较了采用Weibull函数、GMM拟合的风电功率波动特性，可以看出，相比于Weibull分布，采用二维加权高斯混合概率模型得到的概率曲线更加贴合原始样本概率曲线，具有更好地拟合精度，可以用作描述风电出力(pu为标幺值)的波动特性。

表1 二维GMM子成分参数Table.1 Two dimensional GMM subcomponent parameters

图3 实际风电出力GMM拟合Fig.3 GMM approximation of wind power output

3.3 潮流计算

在3.1节所述系统进行潮流计算，在相同的条件下，分别采用常规ABC、LHS和本文方法进行PPF计算，以MCS方法对输入随机变量采样104次结果作为真实后验分布。得到节点17、节点19电压如图4所示。可以看出，ASMC方法较常规ABC而言，其计算获得的概率密度曲线更接近与基于MCS方法得到的真实后验分布，即常规ABC在先验分布与真实后验分布相差较大时，具有容易出现接受率低和准确性不足的情况，图4中ABC计算得到的概率密度曲线明显方差过小，不符合实际运行情况。表2 给出了不同方法下PPF计算的耗时比较，其中基准MCS、LHS、ABC和ASMC仿真时间分别为24.125、12.743、32.378、6.489 s。结合图4和表2可知，常规ABC方法耗时最长，原因在于其具有接受率低下的缺点，选择较低的阈值ε就会带来计算开支时间长的问题。ASMC与LHS方法二者的计算精度相仿，但ASMC方法具有更高的计算效率，在迭代过程中通过扰动核和赋予样本权重来产生样本数据集，可以进一步提高效率。

图4 负荷节点电压的概率分布Fig.4 Probability distribution for voltage of bus

表2 各算法耗时比较Table 2 Time consuming comparison of algorithms

图5为节点10电压的累积概率分布函数，可以看出，该节点电压存在越上限(>1.05 pu)的情况，采用基准MCS、LHS、ABC和ASMC所得的概率分别为5.18%、5.35%、9.46%和5.33%。ABC计算得到的结果偏大，高估了系统潜在运行风险。图6为支路16、17的有功潮流概率分布，ASMC得到的有功功率概率密度分布函数(probability density function,PDF)、累积分布函数(cumulative distribution function,CDF)都和基准MCS非常接近。可以说明本文方法可以获取更准确的概率特性，计算结果可为系统运行提供一定的参考。

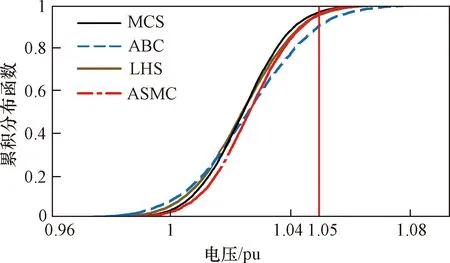
图5 节点10电压累积分布函数Fig.5 Cumulative distribution function for voltage of bus 10

图6 支路16、17有功潮流概率分布Fig.6 Probability distribution for active power flow of line 16，17

图7 不同εT条件下电压概率密度曲线Fig.7 Voltage probability density curve under different εT conditions

对于采用ASMC方法计算PPF而言，阈值ε={ε1,ε2,…,εT}的最小取值εT可能会产生不同的后验估计结果，采用不同的εT取值分别进行概率潮流计算，得到如图7所示的不同结果。可以看出，不同阈值εT取值情况下，得到的状态变量概率密度差异较大，在总体趋势上，随着εT的增大，概率分布越来越分散，即方差在增大。这说明了阈值越小，抽取的样本将全部来自后验分布，对于后验的估计精度更高，产生的近似后验分布差异很小。因此，需综合考虑实际处理问题的复杂性，选择合适的阈值下限。

4 结论

(1)针对新能源风电出力，建立的二维GMM具有更好的拟合精度，可以用作描述风电出力的波动特性，模型的精度和建模效率得到提升。

(2)奇异值分解结合Nataf变换可准确计及输入变量相关系数矩阵非正定的情形，更符合实际应用场景，可适用于新能源风力发电并网及电力负荷具有波动性的未来电网的概率潮流分析。

(3)提出的ASMC方法用于PPF计算效率高，其既能够利用ABC计及状态变量先验信息的思想，又采用样本加权方式和扰动核来避免低接受率情况的发生，最终将状态变量概率分布求解问题转变为一种参数反演问题，为PPF注入了一种新思路。