考虑应力敏感的缝洞型油藏三重介质试井分析理论模型

林永学, 高书阳，曹 耐，蔡 君, 刘善勇, 孙权伟

(1.页岩油气富集机理与有效开发国家重点实验室，北京 100101；2.中国石化石油工程技术研究院，北京 100101；3.中国石油大学(北京)石油工程学院，北京 102249；4.中国石油杭州地质研究院，杭州 310023;5.长江大学录井技术与工程研究院，荆州 434023；6.长江大学地球科学学院，武汉 430100)

碳酸盐岩油气藏资源储量巨大，截至2015年，其石油及天然气资源分别占中国资源总量27%、26.9%，已探明储量逐年增加[1]。塔河奥陶系碳酸盐岩储层是当前中国增储上产的重点区块，该地区岩石基质致密、渗透率低，裂缝主要为全充填裂缝、半充填裂缝，根据岩心敏感性实验发现该地区岩心应力敏感性多表现为强或中强[2-4]。由于存在应力敏感，储层渗透率损失加剧，渗流能力受到制约，产量随之降低。认识和量化裂缝型储层渗透率应力敏感具有重要意义[5-8]。

在储层评价工作中，试井解释作为重要手段，其研究思路是利用压力特征曲线分析解释得到部分初值，将其代入试井模型并微调各参数值，直至得出与实际曲线相符的理论曲线。试井解释所需分析的主要参数有：窜流系数、井筒储集系数、裂缝及溶洞的弹性储容比以及表皮系数等[9]。Raghavan等[10]针对介质变形储层中非线性流体渗流建立了试井解释模型，但未能获得理想解析解。Kikani等[11]在求解试井解释模型的过程中，引入小扰动法得到了较为合理的解析解。部分学者考虑裂缝与井筒连通性，采用Laplace变换和数值反演方法，建立了基岩-裂缝-溶洞组成的三重介质油藏试井解释模型[12-13]。然而，此类研究大多针对常规油气藏，随着油气勘探开发的不断深入，缝洞型油藏在全球范围内被大量发现，对于缝洞型储集层渗流规律及试井分析的研究引起了专家和学者们的极大兴趣。中外学者分别从室内试验和理论研究两个方面开展了缝洞型油气藏的试井研究。熊钰等[14]采用室内实验装置并结合相似理论，通过渗流与管流相结合模拟地层情况的流动，分析真实地层情况下流体流动规律。杜鑫等[15、18]、张福祥等[16]、陈方方等[17]考虑溶洞与井筒间位置关系、压力变化等影响因素，进一步完善了缝洞型试井分析模型。此外，目前考虑应力敏感的试井解释工作也取得了一定进展。廖新维等[19]、段永刚等[20]及王子胜等[21]考虑介质变形(应力敏感)的影响，分别针对超高压低渗气藏、裂缝型油藏、双重介质油藏建立了相应试井解释模型建立。史文洋等[22]基于低渗透裂缝型碳酸盐岩气藏酸压后渗流特征和产量递减规律，建立了考虑酸压改造程度、酸压改造范围、流体低速非达西流动、储层应力敏感的酸压气井渗流模型。孙若凡等[23]考虑启动压力梯度和应力敏感效应的影响，通过耦合原油在基质中的椭圆流动和裂缝中的近径向流动建立两区渗流模型，并应用多井压降叠加原理处理缝间干扰问题。

现针对溶洞尺寸较小的缝洞型碳酸盐岩油藏，结合三重介质流体渗流方程，引入应力敏感影响，建立考虑应力敏感的三重介质缝洞型油藏试井分析模型，并分析所得特征曲线的影响因素，以期对提高油井产能预测可靠性、高效开发这类油气藏具有重要理论意义及现实意义。

1 三重介质缝洞型油藏应力敏感不稳定试井分析模型

1.1 模型假设

假设无限大地层中，井筒位于由裂缝、基质和溶洞构成的三重介质等厚各向同性地层中，根据缝洞型碳酸盐岩储集层特征，将井筒与三重介质储集层简化抽象为如图1所示模型，并采用定产生产方式，模型假设如下：

(1)流体为单相微可压缩流体。

(2)地层中压力于测试前均匀分布。

(3)考虑井筒储集效应及表皮效应。

(4)储层为裂缝-基质-溶洞三重介质，基质与裂缝、裂缝与溶洞间存在窜流，流体经由三重介质渗流之后由井筒采出，基质中与溶洞中的流体经裂缝流入井筒，裂缝、溶洞为主要储集空间，裂缝为流体的主要流动通道。

(5)在上述过程中，流体渗流满足达西定律，且不计重力及毛管压力影响。

图1 井筒-三重介质示意图Fig.1 The sketch of the wellbore in triple media

1.2 三重介质渗流方程及数学模型

模型构建过程中主要考虑裂缝应力敏感效应，根据质量守恒原理建立无限大地层三重介质缝洞型油藏流体不稳定渗流的基本微分方程如下。

裂缝系统:

(1)

基质系统:

(2)

溶洞系统:

(3)

式中：μ为流体黏度，mPa·s；r为地层某点到井筒的距离,m；pf、pv及pm分别为裂缝、溶洞及基质内压力，MPa；kf、kv及km分别为裂缝、溶洞及基质的渗透率，μm2；αf、αv及αm分别为裂缝、溶洞及基质形状因子；t为时间，h；Cf、Cv及Cm分别为裂缝、溶洞及基质压缩系数，MPa-1；φf、φv及φm分别为裂缝、溶洞及基质系统的孔隙度，%。

内边界条件：

(4)

边界条件：

pf(∞,t)=pm(∞,t)=pv(∞,t)=pi，

i=f,m,v

(5)

初始条件：

pj(r,0)=pi,j=f,m,v

(6)

式中：B是储层流体的体积系数；pw是井底压力，MPa；pi是地层压力，MPa；S是表皮系数；q是产量，m3/d；C为井筒储集系数，m3/MPa；rw为井筒半径，m；h为油层有效厚度，m。

对上述渗流模型进行无量纲化处理可得到如下方程组。

(7)

式(7)中：PfD、PmD、PvD分别为裂缝、溶洞及基质内无量纲压力；ωf、ωm、ωv分别为裂缝、溶洞及基质无量纲储容比；CD为无量纲储集系数；tD为无量纲时间；rD为无量纲半径。

进行Laplace变换，得到拉氏空间下考虑井筒储集和表皮效应的无量纲井底压力解为

(8)

(9)

式中：u为拉普拉斯变量；k0、k1分别为零阶和一阶第二类虚宗量贝塞尔函数；λm和λv分别为基质窜流系数和溶洞窜流系数；PvD分别为裂缝、溶洞及基质内无量纲压力；ωf、ωm、ωv分别为裂缝、溶洞及基质无量纲储容比。

为使渗流方程线性化，代入摄动变换函数并通过Stehfest数值反演得无量纲井底压力为

(10)

式(10)中：rfD为无量纲裂缝渗透应力敏感系数；S-1()为Stehfest数值逆变换。

2 考虑应力敏感的模型计算曲线特征分析

图2 无量纲井底压力及其导数双对数曲线(考虑应力敏感)Fig.2 Log-log curves of wellbore dimensionless pressure and its derivative(stress sensitivity considered)

图2中曲线可分为6个典型流动阶段：

第Ⅰ阶段为纯井筒储集阶段，两条曲线为直线段，且斜率为1，其原因在于，此阶段为井筒存储阶段，井筒存储为产量的主要来源。

第Ⅱ阶段中，无量纲压力导数曲线受表皮效应影响呈下降趋势。

第Ⅲ阶段中，无量纲压力导数曲线因径向流出现水平段，此时流体在裂缝中流动。

第Ⅳ阶段中，无量纲压力导数的双对数曲线因溶洞与裂缝间的窜流而出现凹形(受流体在其间流动能力的影响，溶洞与裂缝间发生流体交换需要压力驱动)，无量纲压力导数曲线先下降后上升。

第Ⅴ阶段中，无量纲压力导数的双对数曲线因储层基质系统与裂缝间的窜流而再次出现凹形(基质与裂缝间发生流体交换需要压力驱动)，无量纲压力导数曲线先下降后上升。

第Ⅵ阶段中，无量纲压力导数曲线再次出现水平线，系统达到径向流。

由图2可见，考虑应力敏感对无量纲压力及压力导数双对数曲线有较大影响。在第Ⅰ阶段，应力敏感影响可以忽略；但进入第Ⅱ阶段后，无量纲压力及压力导数曲线均随应力敏感系数增加而有所抬升，且随时间增加，曲线上升幅度越大；其中，在第Ⅲ阶段和第Ⅵ阶段中，随应力敏感系数增加，无量纲压力导数曲线水平段值以0.5为起点逐渐增大，起点处对应应力敏感系数为0，此时无应力敏感效应。上述变化规律的可能原因在于，井筒储集阶段中，井筒供液来源主要为井筒存储，储层的渗流能力对该阶段影响不大；而井筒储集阶段结束后，储层各储集空间成为井筒的供液来源，应力敏感效应制约了储层渗流能力，应力敏感效应越强，驱动流体流动所需压力更高。

3 特征曲线影响因素分析

3.1 表皮系数

采用不同的表皮系数，得到无量纲井底压力及其导数的特征曲线，如图3所示。随该系数增加，无量纲压力导数曲线中第Ⅱ阶段的驼峰升高、形状变陡，无量纲压力曲线整体向上抬升，其原因在于随表皮系数的增加，井底周围的流体流动阻力增大，流体流动所需的压力越大，但表皮系数对无量纲压力导数曲线后期的影响不大。表皮系数越大说明井底受污染越严重。

图3 不同表皮系数下无量纲井底压力及其导数双对数曲线Fig.3 Log-log curves of wellbore pressure and its derivative under different S

3.2 井筒储集系数

如图4所示，采用不同的无量纲井筒储集系数，得到无量纲井底压力及其导数的特征曲线。可见，随该系数增大，无量纲压力曲线向上抬升，无量纲压力导数曲线驼峰向上升高，第Ⅳ、Ⅴ阶段的下凹提前出现。当增加到一定程度时，第Ⅲ阶段将会消失，并直接过渡到第Ⅳ阶段，即直接过渡到溶洞和基质系统间窜流阶段。但无量纲井筒储集系数对压力导数曲线的下凹深度及宽度和最终的径向流阶段几乎没有影响。

图4 不同井筒储集系数下无量纲井底压力及其导数双对数曲线Fig.4 Log-log curves of wellbore pressure and its derivative under different CD

图5 不同溶洞弹性储容比下无量纲井底压力及其导数双对数曲线Fig.5 Log-log curves of wellbore pressure and its derivative under different ωv

3.3 溶洞弹性储容比

计算绘制不同溶洞弹性储容比下，井底压力及其导数的双对数曲线，如图5所示。溶洞的储容比越大代表溶洞储容性越好，无量纲压力导数曲线的第Ⅳ阶段向左移动、第Ⅴ阶段向右移动，且溶洞储容比对压力导数曲线的下凹深度及宽度有影响。其值越大，第一个下凹越深、开口越大，即溶洞与裂缝间窜流越明显，第二个下凹越浅、开口越小，即基质与裂缝间窜流越小，但最后不影响整体径向流阶段。

3.4 裂缝弹性储容比

如图6所示，计算绘制不同裂缝弹性储容比下，井底压力及其导数的双对数曲线。随其值增加，无量纲压力导数曲线第Ⅱ阶段下移，驼峰略有下降，第Ⅳ、Ⅴ阶段向后移，裂缝储容比对无量纲压力导数曲线两处下凹的宽度和深度也有影响，裂缝储容比越大，窜流发生的时间越晚，下凹就会越浅、越窄，第Ⅲ阶段的径向流持续的时间越长。

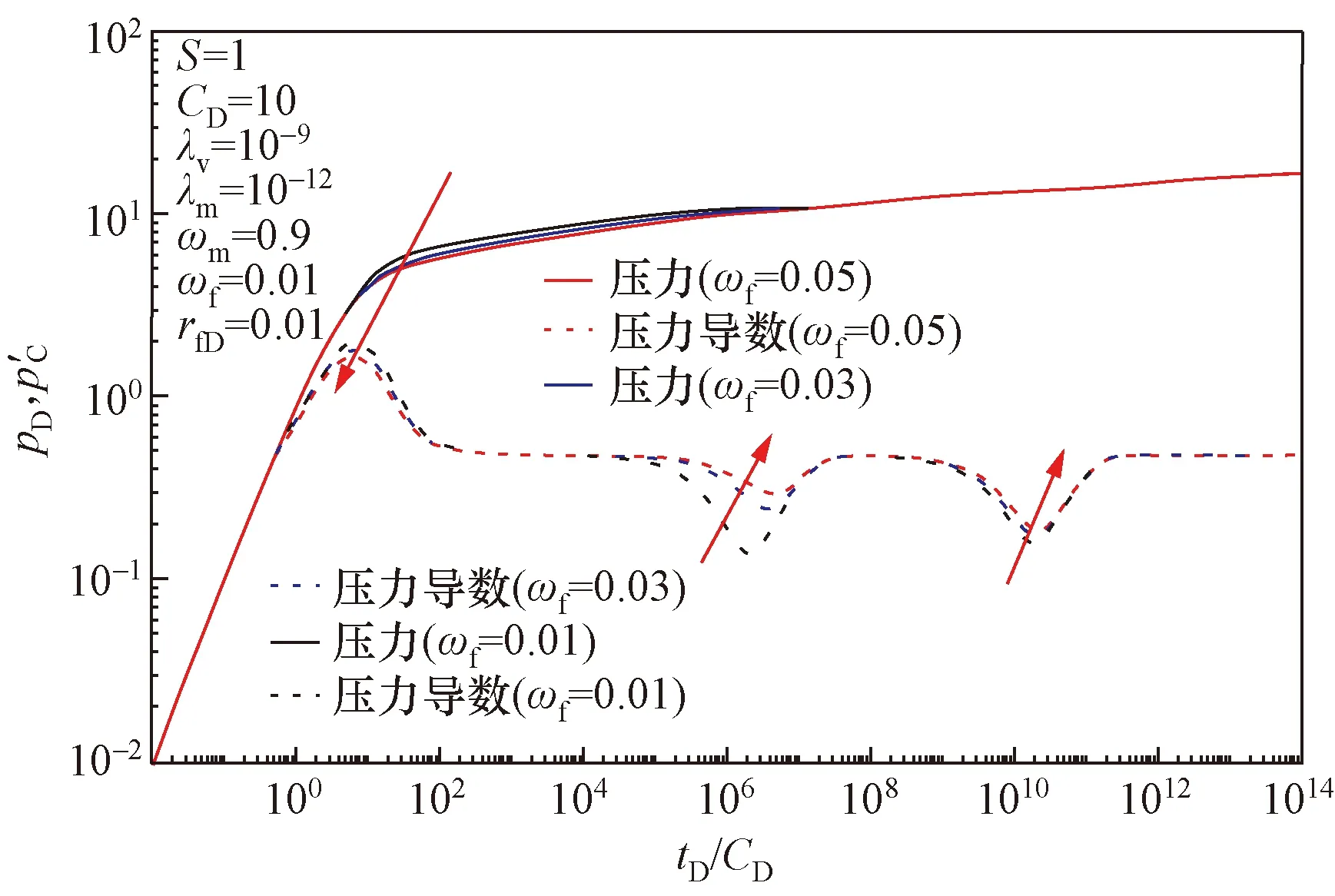
图6 不同裂缝弹性储容比下无量纲井底压力及其导数双对数曲线Fig.6 Log-log curves of wellbore pressure and its derivative under different ωf

3.5 基质弹性储容比

如图7所示，计算绘制不同基质弹性储容比下，井底压力及其导数的双对数曲线。基质储容比仅对第二个下凹阶段有较明显的影响，对其他阶段几乎没有影响，说明基质储容比对溶洞与裂缝间窜流影响可忽略。随着基质储容比的增加，无量纲压力导数曲线第二个下凹的深度和宽度均有所增加，说明基质与裂缝间窜流作用增强。

图7 不同基质储容比下无量纲井底压力及其导数双对数曲线Fig.7 Log-log curves of wellbore pressure and its derivative under different ωm

3.6 溶洞窜流系数

如图8所示，采用不同溶洞窜流系数，得到无量纲井底压力及其导数的双对数曲线。溶洞窜流系数对第一个下凹阶段有较明显的影响，而对基质与裂缝间窜流引起的第二个下凹形态及出现时间无明显影响。随着溶洞窜流系数的增加，裂缝与溶洞间窜流提前发生，无量纲压力导数曲线第一个下凹阶段的下凹越靠左，但下凹的形状不受影响，第Ⅲ阶段持续的时间也随之减小。

图8 不同溶洞窜流系数下无量纲井底压力及其导数双对数曲线Fig.8 Log-log curves of wellbore pressure and its derivative under different λv

3.7 基质窜流系数

如图9所示，采用不同基质窜流系数，得到无量纲井底压力及其导数的双对数曲线。相对于基质窜流系数对第二个下凹阶段较明显的影响，其对第一个下凹阶段影响可忽略。随着基质窜流系数的增加，裂缝与基质间窜流提前发生，无量纲压力导数曲线第二个下凹阶段的下凹越靠左，但其对下凹形状影响并不明显。

图9 不同基质窜流系数下无量纲井底压力及其导数双对数曲线Fig.9 Log-log curves of wellbore pressure and its derivative under different λm

基于对上述影响特征曲线形态的储层参数分析，可知在实际试井解释中，可根据试井曲线的阶段形态确定储层类型，试井曲线中的两个凹形可作为判断三重介质储层的特征；依据已分析影响参数与曲线形态的相关关系可在试井解释曲线拟合过程中合理选择影响参数，合理评价目标储层。

4 结论

生产初期，流体压力大，储层承受有效应力较低，应力敏感效应较弱；开发后期，井底压力下降，储层承载有效应力增大，渗透率因应力敏感造成损失加剧，应力敏感影响不可忽视，对于强应力敏感性储层(如奥陶系一间房组储层)，渗透率应力敏感的准确表征有利于提高产能预测精度。

无量纲压力及压力导数曲线随应力敏感性增强而整体向上抬升，随着时间的增加，上升幅度逐渐增大。可将无量纲压力导数曲线的水平段取值作为判断是否需要考虑应力敏感的特征值，若其水平段值大于0.5则应考虑应力敏感的影响，否则，则无需考虑，直接得出不考虑应力敏感的无量纲井底压力解。

试井解释曲线的“双下凹”形态可作为判断三重介质缝洞型油藏的曲线特征。井筒储集系数的增大会造成“双下凹”的提前，溶洞储容比与裂缝储容比对两个凹形的形态及出现时间均有影响，基质储容比影响第二个凹形出现的早晚与形态，溶洞窜流系数与基质窜流系数分别仅影响第一个凹形及第二凹形出现的早晚。应用三重介质缝洞型试井模型时，除应结合上述影响规律外，还应考虑表皮系数、无量纲井筒储集系数及裂缝、溶洞储容比对曲线第Ⅱ阶段驼峰形态的影响，最终确定储层参数。