固相条件下研磨屑解毒六价铬机理及动力学规律研究
刘友舫,吴卫林,郭鹏飞,胡长江,高铭政
(安徽浩悦环境科技有限责任公司,安徽合肥231145)
镀铬、皮革、化工、印染、造纸等领域产生的含铬废水会导致土壤与地下水污染。铬在环境中的存在形式主要有三价铬和六价铬两种,其中六价铬是毒性最强的价态形式,溶解性大,迁移能力强,易扩散,可造成人体器官损伤、癌变,对人畜及农作物危害很大,给环境质量与人身健康带来很大威胁,其中含铬废渣六价铬最高可达到40%(三氧化铬),总铬最高可达到45%。国内外对铬渣的处理与综合利用方法有3种:固化法、还原法及络合法。国外主要采用固化填埋方法,但消耗大量水泥,成本很高。高温固相还原法是加入木屑、稻壳、亚铁盐、碳粉为还原剂,在高温条件下将铬渣还原成三价铬降毒,最终以玻璃态形式存在,此法是较好的处理方式,但耗能高,会产生污染气体。湿法还原法在场地修复或实验室研究加入铁屑与改性纳米零价铁的还原剂、亚铁离子如亚铁盐、含硫化物的还原剂,理论效果较好,但是还原剂成本较高,产生很多废水、废渣,造成二次污染。本研究在固相条件下,对含铬废渣中六价铬解毒,将毒性较高的六价铬还原成毒性较低的三价铬后,加入固化剂石灰与水泥进行稳定化处置。
1 实验部分
1.1 材料与仪器
浓硝酸、浓硫酸,优级纯;氢氧化钠;含铬废渣;研磨屑(金属机械打磨产生,单质铁与二价铁的百分含量约40%~70%);二苯碳酰二肼;实验蒸馏水;pH试纸;烧杯(250 mL、500 mL);玻璃棒。
TU 1901紫外分光光度计,北京普析;Optima8000型等离子耦合电感发射光谱仪,珀金埃尔默仪器(上海)有限公司;HTZF-1A型制样粉碎机;圆孔筛:20目、50目、100目、150目。
1.2 实验方法
1.2.1 pH
20℃下,取浸出液六价铬浓度为5 860 mg/L的含铬废渣,用粉碎机打磨15 min,过100目的圆孔筛,得到粒径不小于100目的铬粉,用1 mol/L的硫酸溶液和2 mol/L的氢氧化钠溶液配制pH分别为2、3、4、5±0.1的酸性溶液,设置4组实验,称取100 g铬粉4份置于烧杯中,称取85 g的研磨屑4份放入上述4个烧杯中,搅拌均匀,向上述混合物中加入不同pH的酸性溶液120 mL混合放置,进行固相反应,根据反应时间取样分析上述4个体系的六价铬含量。
1.2.2 铬渣粒径
设置4组实验,20℃下用粉碎机将六价铬浓度为5 860 mg/L的含铬废渣粉碎打磨15 min,用10目、50目、100目、150目的圆孔筛筛选,得到目数不低于10目、50目、100目、150目的铬粉,用硫酸与氢氧化钠溶液配制pH为2的酸液,称取上述不同目数的铬粉100 g,依次加入85 g的研磨屑,搅拌均匀,分别量取120 mL酸液置于上述不同类别的混合物中,搅拌均匀固相反应,根据反应时间取样分析上述4个体系的六价铬含量。
1.2.3 含水率
设置三组实验,实验前用粉碎机打磨、圆孔筛筛选得到不低于100目的铬粉,配制pH为3的酸性溶液,20℃下,分别称取100 g六价铬浓度为5 860 mg/L经过加工后的铬粉3份,依次加入85 g的研磨屑,搅拌后,量取不同体积pH为3的酸性溶液置于混合物中,混合均匀,得到含水率分别为30%、45%、60%±1%的反应体系,进行固相反应,根据不同反应时间,取样分析上述六价铬含量。
1.2.4 六价铬初始浓度影响
用粉碎机和100目的圆孔筛加工不同六价铬含量的铬渣,得到浸出液六价铬分别是5 860 mg/L,9 608 mg/L,11 850 mg/L的铬粉,分别称取100 g上述加工后的铬粉3份,配制pH为3的酸性溶液,设置三组实验,20℃下,称取120 g研磨屑,分别量取140 mL酸液置于上述混合物中,搅拌均匀固相反应,根据反应时间取样分析上述3个体系的六价铬含量。
1.2.5 温度
实验前配制pH为3的酸性溶液,设置三组实验,称取100 g六价铬浓度为5 860 mg/L的铬粉3份,称取85 g的研磨屑分别置于上述烧杯中,搅拌均匀,向上述混合物中加入配制的溶液120 mL混合搅拌固相反应,将上述3份体系分别置于5℃、20℃、(35±1)℃反应,根据反应时间取样分析上述3个体系的六价铬含量。
1.3 反应模型建立
对于六价铬氧化还原解毒反应,很多人已经反复论证可用一级动力学分析反应过程(25.26.27),假定研磨屑在酸性条件下还原六价铬进行固相反应与一级动力学规律模型一致,即反应速率反应式:

式中:c与c是反应0时刻与t时刻固相体系六价铬浓度;K是一级反应动力学速率常数,绘制ln(c/c)对时间t的曲线斜率计算得到。
2 结果与讨论
2.1 pH对六价铬还原反应的影响
从图1可知,研磨屑在酸性条件下还原六价铬固相反应基本符合一级动力学规律,pH在2~5范围内,六价铬反应速率常数逐渐减小,体系随着氢离子浓度增大,反应常数逐渐增大,如表1所示,20℃下,六价铬目数为100目,pH为2时,速率常数是pH为3、4的1.63倍、2.47倍;pH=2,反应三天,六价铬解毒为三价铬的效率为99.28%;在pH=3条件下,同样的反应时间,六价铬降解率是95.76%;增加pH至5,六价铬降解率至51.32%,主要原因是酸性条件下可以催化Cr(VI)还原,氢离子浓度越高,越有利于Cr(VI)还原降解。

图1 pH对六价铬反应动力学的影响
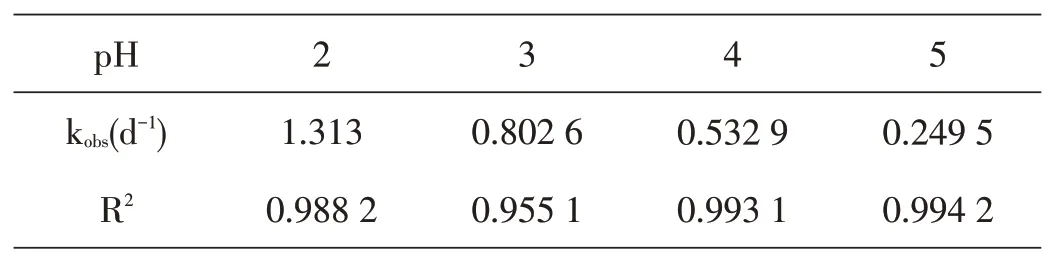
表1 不同pH值与六价铬反应速率常数的关系
2.2 铬渣粒径大小对六价铬还原反应的影响

图2 铬渣不同粒径对六价铬反应动力学的影响
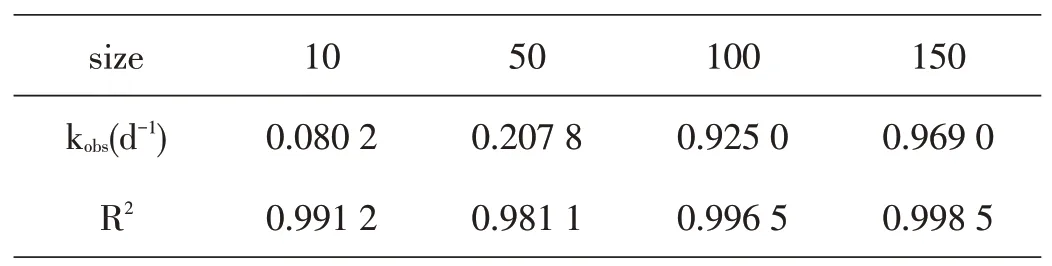
表2 不同目数与六价铬反应速率常数的关系
如图2所示,研磨屑在酸性条件下还原六价铬固相反应基本符合准一级动力学规律,R大于0.98,含铬废渣的粒径大小对六价铬还原解毒反应有较大影响,在温度20℃、pH=3的条件下,可以明显发现随着六价铬目数的变大,即粒径变小,固相反应速率常数逐渐增大,其中目数为150目时,还原反应速率常数分别 是目数为10目、50目的12.1倍、4.8倍,这是因为随着铬渣粒径变小,比表面积增大,分子活化数增多,从而增大还原剂研磨屑与六价铬的反应速率。
2.3 含水率对六价铬还原反应的影响
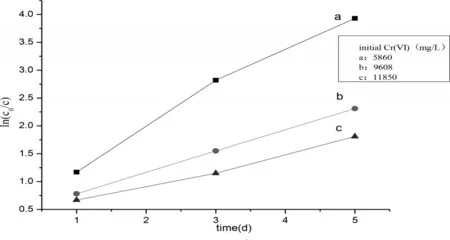
图3 不同含水率对六价铬反应动力学的影响

表3 不同含水率与六价铬反应速率常数的关系
如图3所示,在温度20℃、通过加入pH=3的酸性溶液配制成不同含水率的六价铬还原反应体系,反应3天,含水率为60%、45%、30%的反应体系六价铬浓度分别减少了5 782 mg/L、5 511 mg/L、4 832 mg/L。不难发现,随着含水率增高,反应速率不断增大,体系含水率为60%时的反应速率常数分别是45%、30%的1.91倍、2.24倍,这是因为在初始pH相同的条件下,含水率越高,还原剂研磨屑与含铬废渣粉末混合越均匀,固相反应越充分,越有利于Cr(VI)还原降解。
2.4 六价铬初始浓度对六价铬还原反应的影响
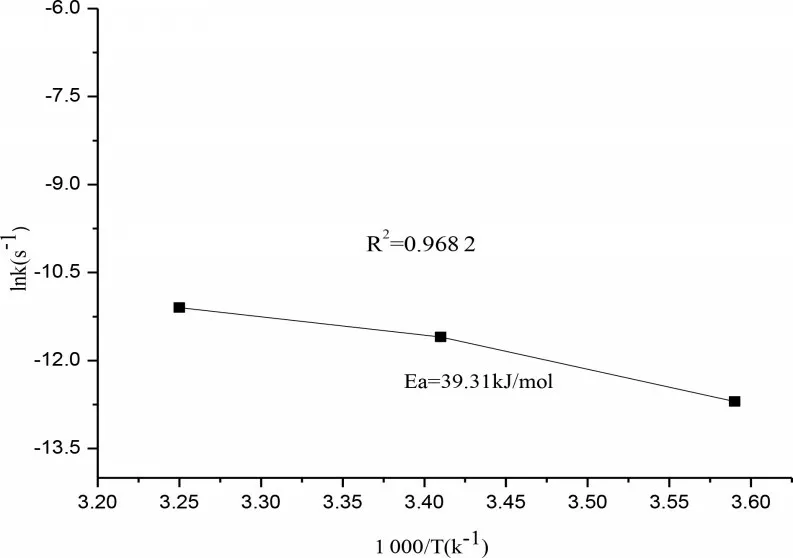
图4 六价铬不同初始浓度对六价铬还原反应动力学的影响
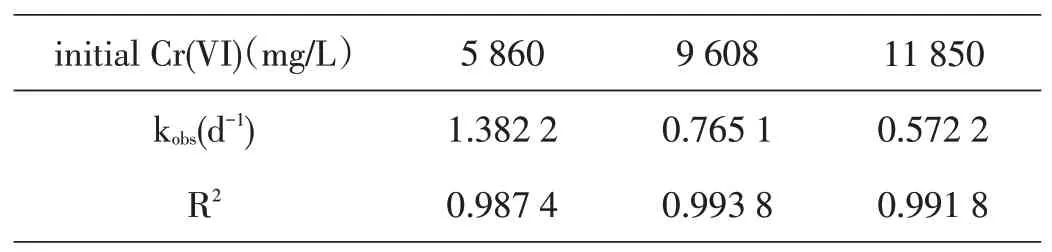
表4 六价铬初始浓度与六价铬反应速率常数的关系
在温度20℃、pH=3的条件下,加入不同六价铬初始浓度的铬粉与研磨屑固相反应,符合准一级动力学反应规律,从图4可以证明,六价铬初始浓度为5 860 mg/L的反应速率常数是六价铬初始浓度分别是9 608 mg/L、11 850 mg/L的1.8倍、2.41倍。在加入酸液体积相同、铬粉目数相同的前提下,还原速率随六价铬初始浓度的增大而减小,主要是因为在固相条件反应中,铬粉会被包裹在研磨屑里,发生团聚,随着单位质量铬粉中六价铬含量增高,不能与研磨屑均匀充分反应。
2.5 温度对六价铬还原反应的影响
图5 不同温度对六价铬还原反应动力学的影响

表5 温度与六价铬反应速率常数的关系
在pH=3、含水率45%条件下,研究体系中温度对铬粉固相还原反应的关系,由表5可以发现,当温度为35℃时反应速率常数k为1.313 2,温度降到20℃、5℃时,k分别降低到0.781 4、0.257 5,R大于96.6%,主要是因为随着温度升高,固相反应中的分子无规则运动加快,有效反应分子数增多,反应速率常数增大。
为进一步研究研磨屑与六价铬固相还原反应机理,研究温度与反应速率常数的关系,建立阿伦尼乌斯经验公式如下:
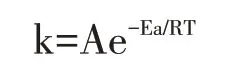
式中,Ea是反应活化能,kJ/mol;A是指前因子,s,两边取对数得到:lnK=lnA-Ea(1/RT);R-摩尔气体常数,0.008 314 kJ/(mol·K);T-热力学温度,K。
如图5所示,根据直线的截距和斜率,得到固相反应六价铬的指前因子A为79.67 s,反应活化能Ea为39.31 kJ/mol,因此温度对反应常数影响关系式为:K=79.67e,不难发现温度越高,反应速率常数越大。
3 结论
酸性体系中,研磨屑还原六价铬固相还原反应过程中,在pH=2~5时,随着酸性变强,还原速率常数变大,铬渣经过机械加工后目数越大,粒径约小,越有利于反应进行,符合准一级动力学规律;混合体系含水率在30%~60%时,含水率越高,越利于加快六价铬还原反应;温度为20℃,含水率45%体系中,六价铬初始浓度越小,反应速率常数越大,温度在5℃~35℃,模拟阿伦尼乌斯公式得到反应活化能Ea为39.31 kJ/mol。

