考虑人-结构耦合作用的室内大跨钢连廊振动舒适度分析

官京城， 谈丽华， 陈 鑫， 张志强， 常 瀚

(1 苏州科技大学江苏省结构工程重点实验室， 苏州 215011； 2 中衡设计股份集团有限公司， 苏州 215021； 3 东南大学土木工程学院， 南京 210096)

0 引言

近年来，由于建筑功能的要求和结构技术的发展，在城市大型公共建筑中，大跨度柔性室内连廊越来越多地得到了应用。纤细优美的外形、轻质高强的钢材和空间转换的功能使得这类连廊通常具有质量轻、刚度小、跨度大等结构特点，然而其在动力荷载的作用下极易发生较大的结构振动，影响结构正常使用乃至安全寿命。

研究表明按当前规范设计的钢连廊类大跨度结构通常具有阻尼小、基频低的特点[1-2]，因此，尽管相对于人行天桥，室内连廊不受风荷载的影响，但长期行人荷载导致的日常使用问题一直受到设计人员关注。一方面，日常行人的步频分布在一个较窄的频带1.60～2.40Hz范围内，这与室内钢连廊的自振频率较为接近，极易诱发较大的结构振动，从而影响行走的舒适性。另一方面，作为荷载载体的行人自振频率实测结果在2.0～3.0Hz的范围内[3]，且质量相对于轻质的钢连廊不容忽视，这些将导致行人与连廊之间的相互作用对动力分析结果的影响[4-6]。

随着对人群荷载下振动舒适度研究的深入，人-结构之间的相互作用逐渐引起学者们的关注。Hawryszków等[7]通过对人群作用下人行天桥的理论计算与实测结果进行对比分析，发现行人的驻留降低了人行天桥的均方根加速度响应。 Ahmadi等[8]利用一块7.5m×5.0m矩形板的空载和承载试验对比发现，人-结构耦合作用显著地增大了结构的阻尼比，且略微增大了结构前三阶振动频率。张志强等[9-10]对高铁站房大跨楼盖在人群荷载激励下的响应进行了数值模拟和实测研究，现场实测的峰值加速度最多比计算值小27.94%，并建议在对建筑结构的振动舒适度分析时应考虑留驻人群效应。从上述研究可见，不考虑人-结构相互作用时，人群荷载作用下的结构数值模拟响应通常大于实测结果。为此，众多学者尝试从理论和数值模拟角度对人-结构耦合作用进行研究。Shahabpoor等[11]通过简化人-结构耦合系统，建立人站立时人-结构耦合振动方程。Caprani等[12]首先建立单人与结构耦合振动方程，并扩展建立人群-结构耦合振动方程，最后建立了针对三种不同简化形式的人-结构耦合系统振动方程。王卫荣等[13]建立了满足双向单人或双人激励的人-四边简支板的耦合振动方程，相对于非耦合模型，其计算结果更加接近实测值。尽管已有较多的工作关注人-结构耦合作用，但从工程角度来看研究多集中于大跨楼盖和人行天桥。室内大跨钢连廊由于承受荷载的不同导致了其结构特点与前述结构有所差异，且此类结构与人相互作用的相关研究目前相对较少。

为此，本文围绕苏州文博中心36.1m长的室内钢连廊开展人-结构耦合作用对室内钢连廊振动舒适度分析影响的研究。首先，选取两类人体质量-弹簧-阻尼模型(Mass-Spring-Damper，MSD)的参数，建立人-钢连廊的耦合振动动力方程，并对其中的关键参数进行讨论。随后，基于试验获取的单人连续行走公式，建立钢连廊人群荷载模型。最后，利用有限元软件实现人-钢连廊耦合振动问题求解，并讨论人体MSD模型参数、步行频率、人群密度等因素对耦合振动模型分析结果的影响。

1 人-结构耦合作用模型

1.1 人体动力模型

在考虑人-结构耦合作用时，将人体与结构作为相互独立而又相互作用的两个动力系统，其中人体是一个多自由度的、复杂的、具有随机性的非线性动力系统。为简化分析，人体可简化为具有质量、刚度和阻尼的有限自由度系统，目前主要有单自由度有阻尼模型、双自由度有阻尼模型以及多自由度有阻尼模型等。

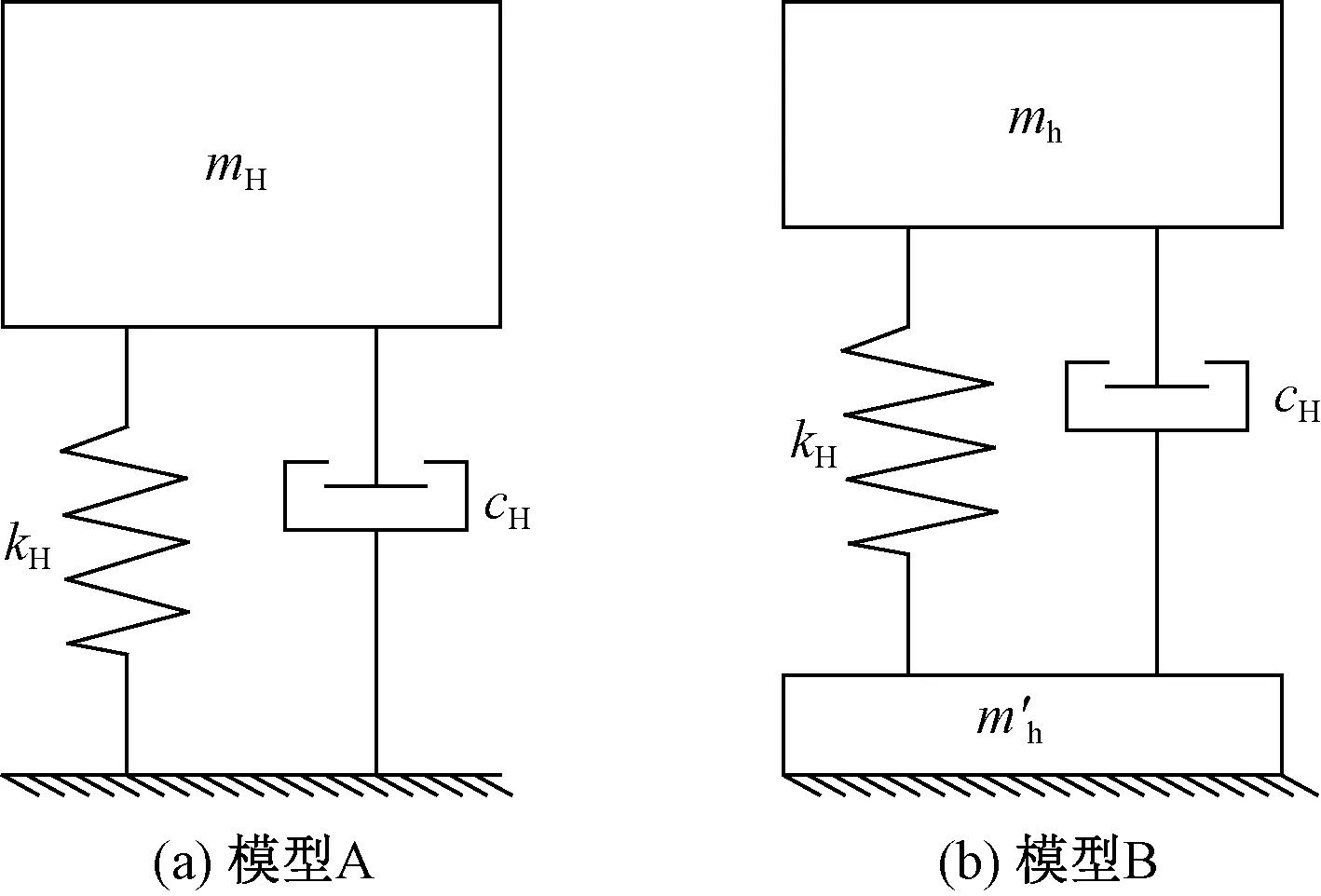
图1 人体简化动力模型

(1)质量-弹簧-阻尼系统

(1)

(2)

(2)质量-弹簧-阻尼-耦合质量系统

(3)

(4)

研究表明，不同研究者针对上述模型获取的参数具有一定的离散型，且外国人体数据也与中国人体数据有一定的差异性。为此，课题组针对质量-弹簧-阻尼系统，开展了25人4种步频(1.5～2.1Hz)的单人行走试验[14]，并识别了人体频率和阻尼，结果见表1。质量-弹簧-阻尼-耦合质量系统则直接选用Javier Fernando等[3]的试验数据均值，耦合质量约为人体质量的13%。

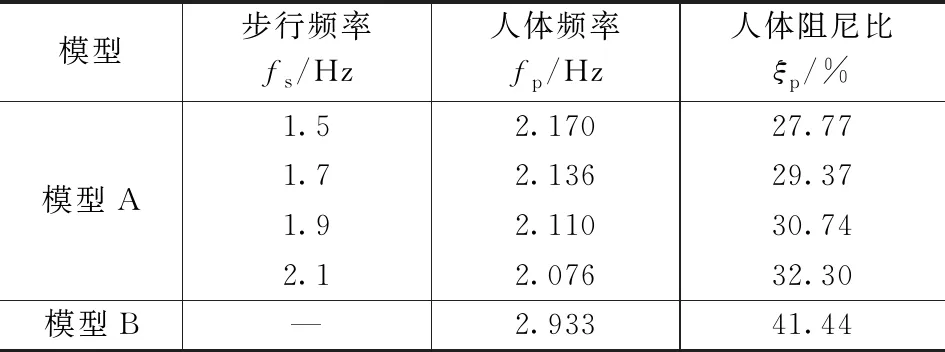
人体MSD参数 表1

1.2 人-结构耦合动力方程

针对室内大跨钢连廊，建立人-结构耦合动力模型如图2所示，其中图2(a)，(b)分别为基于人体模型A和人体模型B的人-结构耦合作用体系，连廊模型两端简支。基于动力平衡方程(5)，分别建立人体模型A，B作用下的人-结构耦合动力方程，如式(6)，(7)所示。

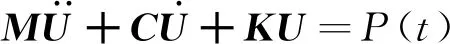
(5)

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；P(t)为激励荷载；U为位移矩阵。

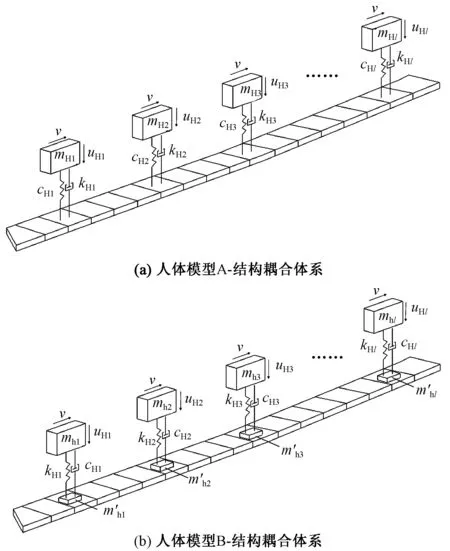
图2 人-结构耦合作用动力体系

(1)人体模型A-结构耦合体系振动方程

(6)

(2)人体模型B-结构耦合体系振动方程

(7)

(8)

(9)

(10)

(11)

uT=[uH1,uH2,…,uHl]

(12)

(13)

(14)

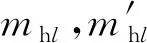
2 钢连廊人群荷载模拟

2.1 单人步行连续荷载模拟

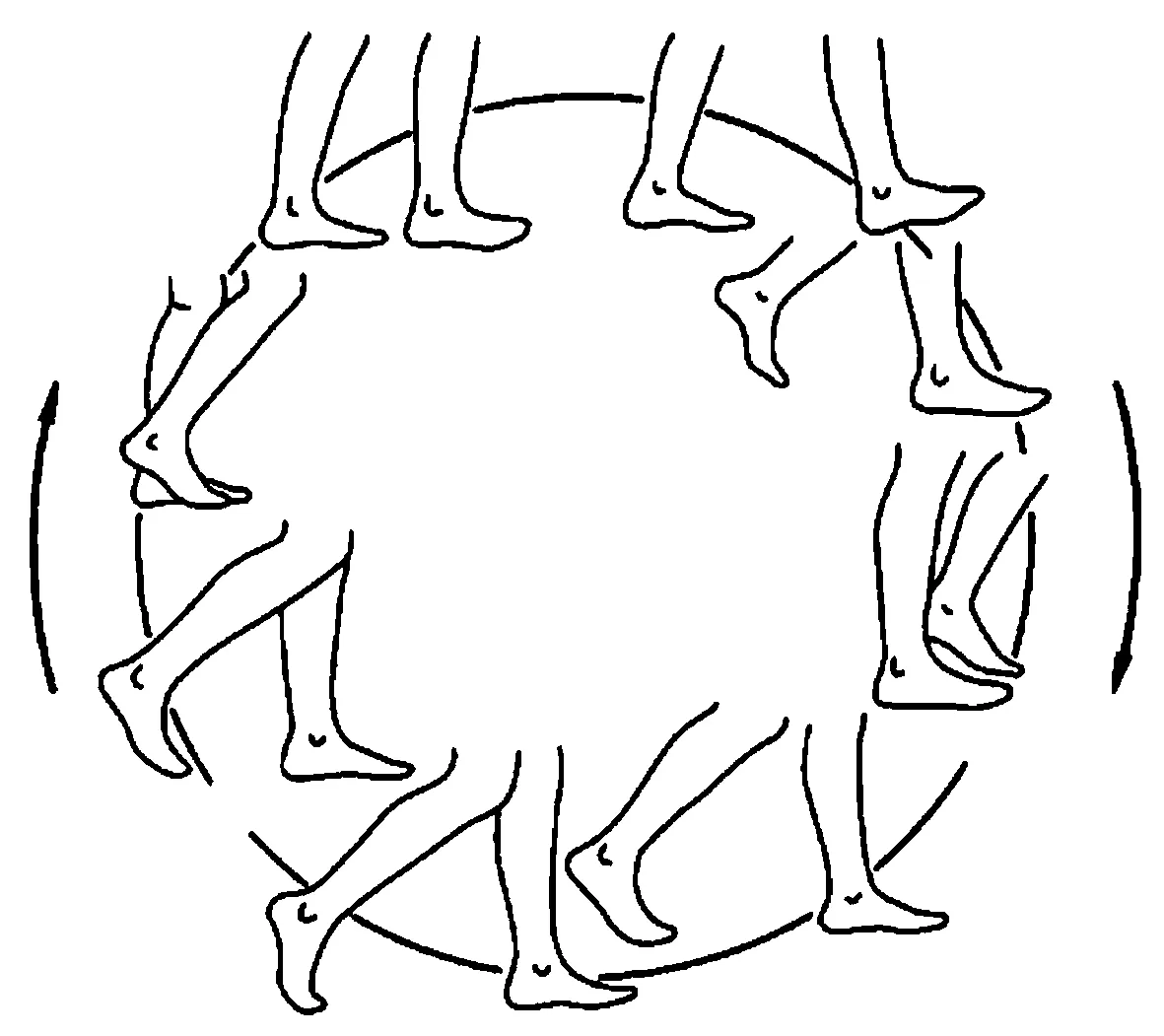
图3 步态周期示意图

图3是行人行走的过程中一个完整的步态周期，在行走时人的重心总是在上下波动，对地面施加的作用力也在不断变化，目前单人连续荷载模型主要有确定性模型和随机模型两类，工程上应用较多的是确定性的步行荷载曲线[10]：

(15)

式中：G为行人体重；n为函数的阶数；t为时间；fs为竖向步频；αi为第i阶傅里叶级数的系数，即第i阶荷载谐波的动力因子(DLF)；Φi为第i阶荷载的相位角。

为了获取适用于中国人体的单人连续步行荷载曲线，课题组开展了66人频行频率控制在1.5～2.3Hz间的单人连续行走试验，统计获取了前三阶谐波的步行荷载曲线参数如下[15]：

α1=0.261 1fp-0.210 9

α2=0.090，α3=0.077

Φ1=Φ2=Φ3=0

式中fp为竖向步频。

假定单个行人体重取700 N，单人步频分别取1.7，1.9，2.1Hz时步行荷载时程曲线如图4所示。

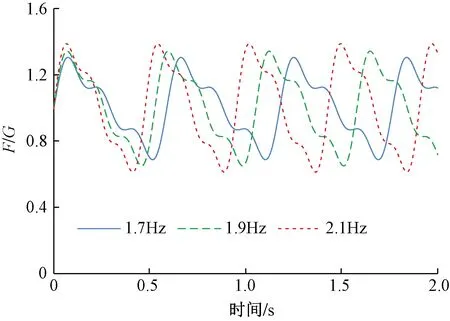
图4 单人步行荷载时程曲线图

图5 苏州文博中心

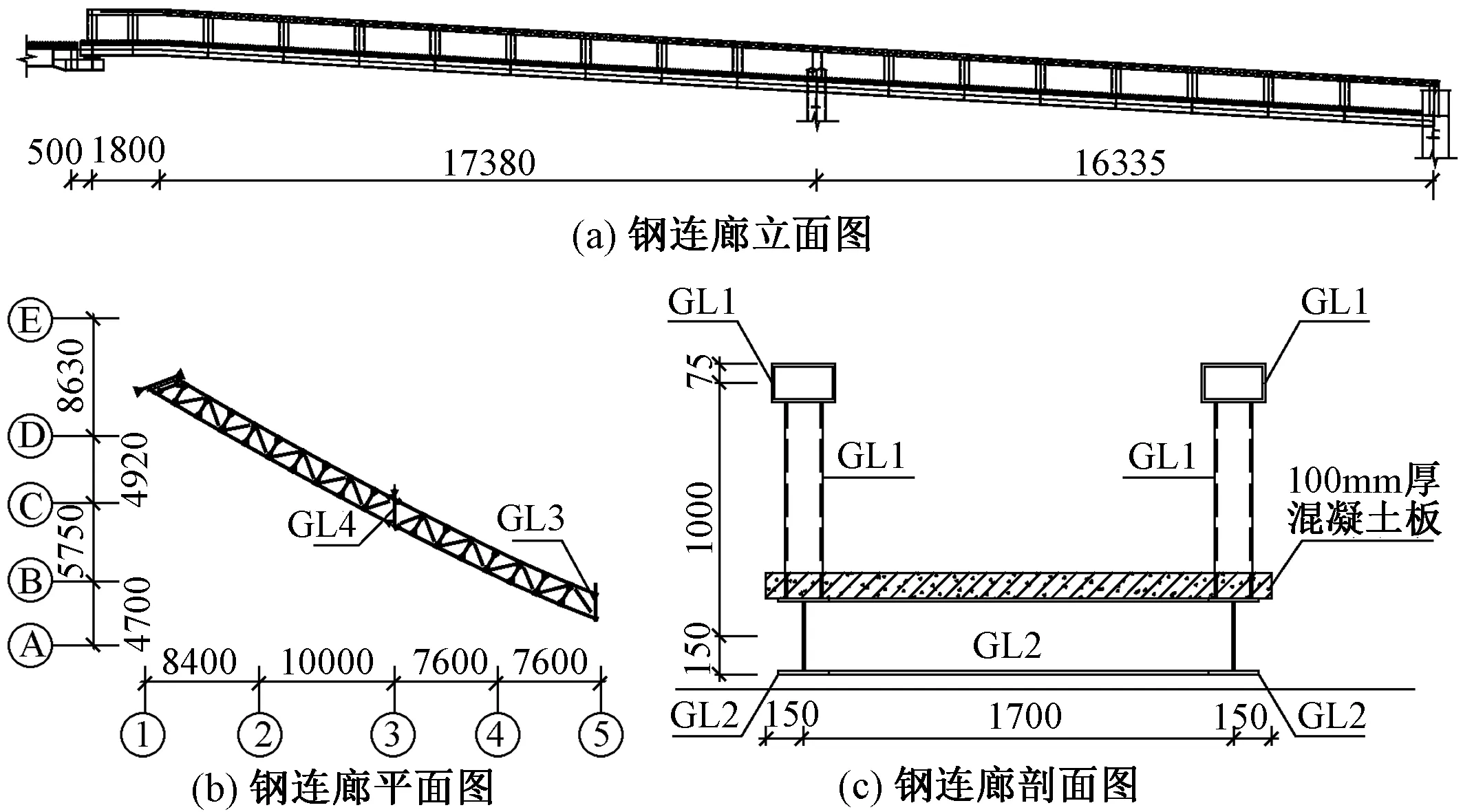
图6 钢连廊布置图

2.2 人群荷载模拟

对于单人步行荷载模型而言，模型中各类参数都是确定的，在一定的步频下不会发生变化。但是对于人群荷载，参数具有很大的随机性，很难保证每个行人的步频都是一致的，而且行人之间的步行作用效果可能相互叠加，也可能相互抵消。因此准确建立人群荷载模型对人群作用下的振动舒适度分析具有必要性。

假设每个人的步行荷载函数均采用式(14)，由于每个人的步频不一致，具有随机性，对此法国人行桥指南[16]指出将w个行人随机在桥上行走的作用效果转化为Wp个完全同步行人的作用效果，从而简化了人群荷载计算的复杂程度，并给出了不同人群密度下等效人数Wp的计算公式，见式(16)和式(17)。

人群密度小于1.0人/m2时：

(16)

人群密度大于1.0人/m2时：

(17)

式中：w为行人总数；ξ为结构的阻尼比。

当人群密度大于1.0人/m2时，行人想自由行走已经比较困难，法国人行桥指南[16]指出，连续的高密度人群在桥上流动的时候可以将其比作连续的物质流，此时，人群相互同步的概率已远远大于人群密度较小时，行人基本同频率走动。

3 人-钢连廊耦合振动分析

3.1 结构分析模型

3.1.1 工程概况

苏州文博中心(图5)位于苏州滨湖路与人民路交叉口西南角，由苏州大剧院和吴江博览中心组成，建筑地上建筑面积约为100 000m2，建筑地下建筑面积约为120 000m2，建筑总高度约54.17m。其中，苏州大剧院西南侧有一用于观光游览的大跨度钢结构连廊(图6)，该连廊总长约36.1m，由两榀两跨空腹钢桁架组成，跨度分别约为19.73m和16.34m，中间跨为单侧支撑，单榀空腹钢桁架上下中心弦距离1.0m，连廊上下高度差约2.0m。根据结构具体形式和专家建议，结构阻尼比取为0.02。

3.1.2 有限元模型

建立该大跨度钢连廊结构有限元模型如图7所示，其中混凝土板采用壳单元建立，杆件均采用三维梁单元。混凝土板采用C35混凝土，弹性模量3.15×107kPa，泊松比0.2，密度2 550kg/m3，板厚100mm。钢材均采用Q345钢材，弹性模量2×108kPa，泊松比为0.3，密度为7 850kg/m3。其中钢连廊栏杆及栏杆扶手采用GL1，图6中未注明截面均采用GL2，钢连廊中各杆件的截面如表2所示。

杆件截面型号 表2

为考虑人-结构耦合作用对结构动力特性和响应的影响，并研究其影响规律。分析时假定人体质量为70kg，引入1.1节所讨论的人体动力模型，模型模态参数如表1所示，换算得到对应的物理参数见表3。

根据2.2节所述的人群荷载模拟方法，整个连廊的面积约70.73m2，当人群密度为0.5人/m2和1.0人/m2时，由式(16)和式(17)可知，连廊上的等效同步人数分别为9人和15人。假定任意时刻钢连廊上都有相应人群密度的等效同步人数的行人走动，且人群荷载均匀的分布在整个连廊的平面上，建立分析工况如表4所示。

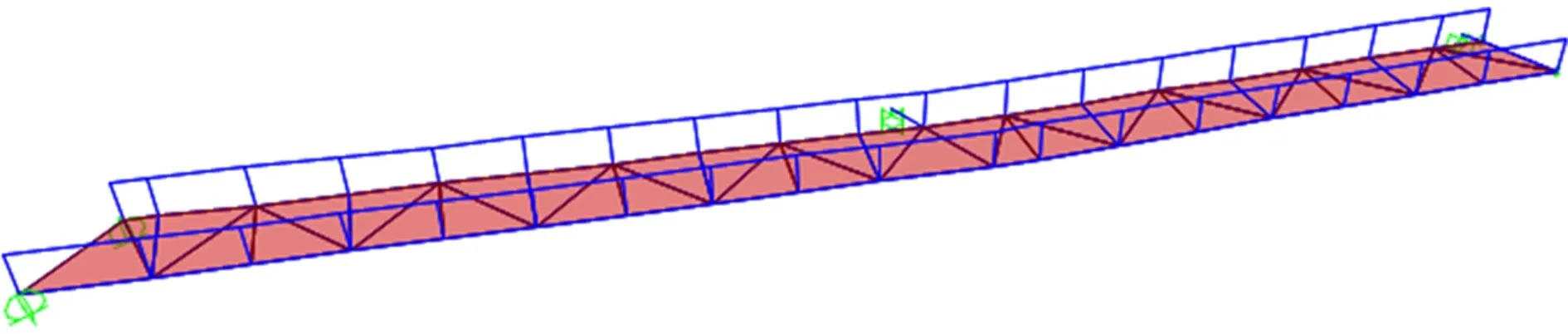
图7 钢连廊有限元模型

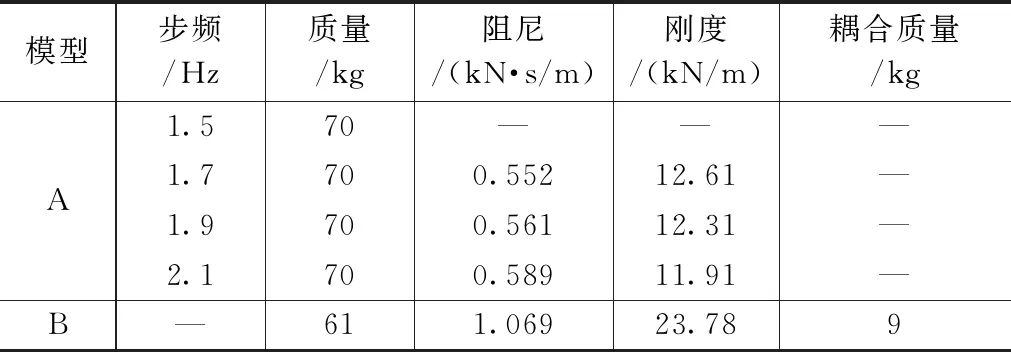
人体模型参数 表3

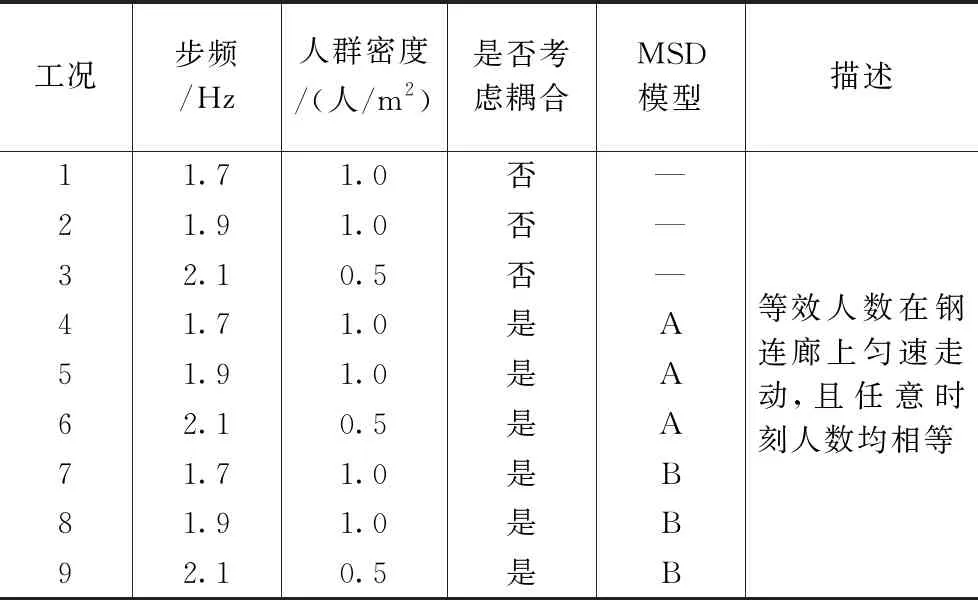
分析工况 表4

3.2 人-结构耦合作用对动力特性的影响

首先不考虑人-结构耦合作用，采用Eigen向量法对钢连廊进行动力特性分析，得到钢连廊前三阶振型以及频率，如图8所示。可见钢连廊第1阶振型为横向，第2阶为竖向反对称振型，且第1阶竖向振型频率为3.39Hz，接近3Hz的频率限值。

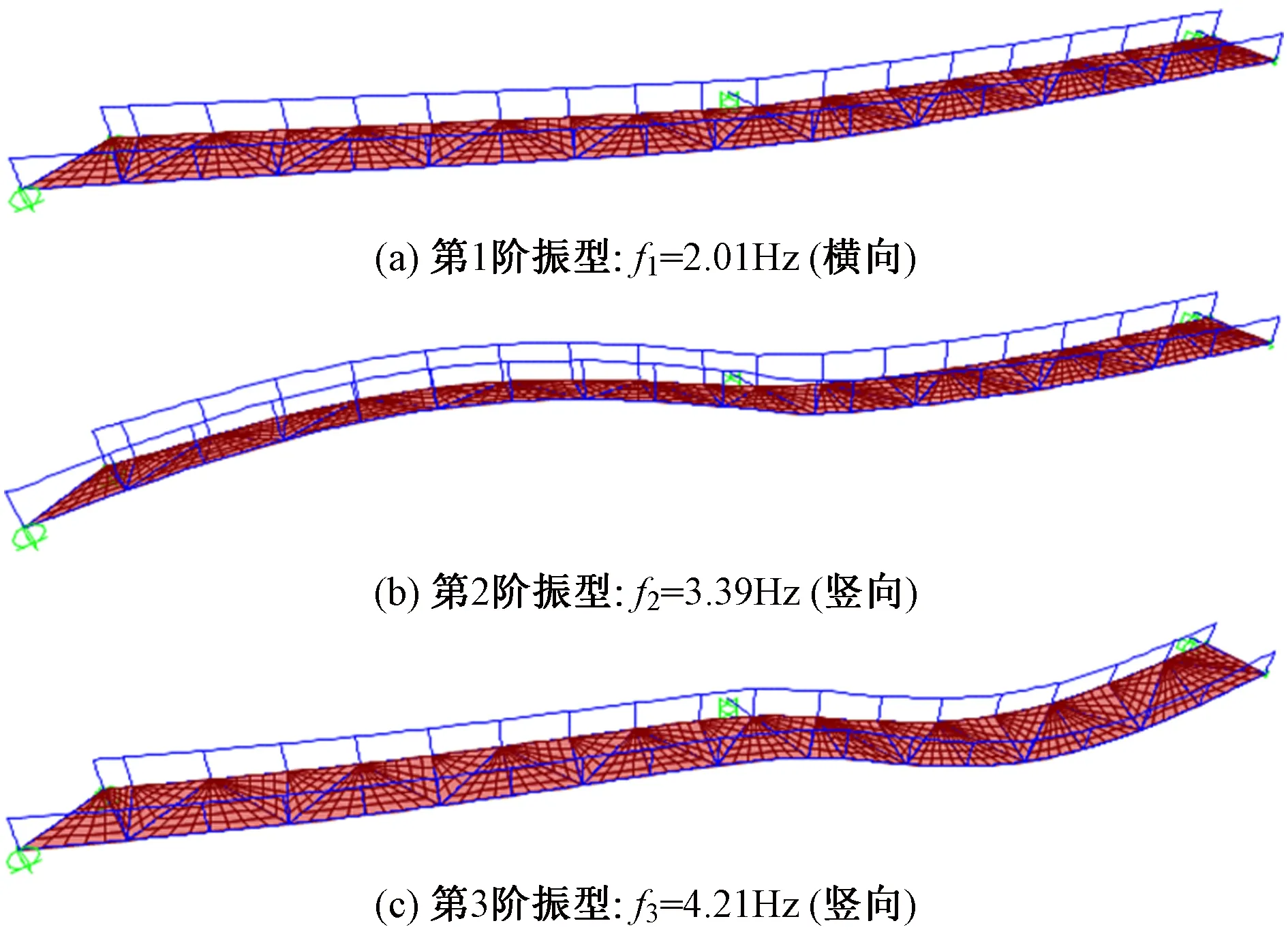
图8 钢连廊振型

当仅考虑人群荷载作用在钢连廊上时，并没有改变钢连廊本身的特性，所以钢连廊的自振频率和钢连廊的振型并没有发生变化，即工况1，2和3下的钢连廊动力特性不改变。在考虑人-钢连廊耦合作用后，由于人体模型的贡献，整个钢连廊结构的质量、刚度、阻尼均发生了改变，钢连廊的动力特性发生改变。由于人-钢连廊相互作用，钢连廊在动力特性分析后产生了新的模态，且新的模态均产生在未考虑人-钢连廊耦合作用的第1阶模态与第2阶模态之间。表5给出了各工况下剔除新增模态后的前三阶频率，对比可见：1)考虑人-结构耦合作用后，钢连廊的前三阶频率均有不同比例的变化，当耦合的MSD模型频率与结构的振动频率接近时，相对于其他工况对结构自振频率的影响较大；2)耦合系统质量分布不同对结构的自振频率影响不同，同时由于钢连廊质量为34 732.3kg，相对于耦合的等效人数(最大15人)质量大很多，因此耦合作用对结构整体自振频率影响总体较小，最大仅为5.055%。

3.3 人-结构耦合作用对动力响应的影响

对钢连廊进行动力时程分析，得到各工况下钢连廊跨中节点动力响应峰值加速度如图9所示，对比可见：1)在考虑人-结构耦合作用后的工况下钢连廊的振动加速度总体呈现减小的趋势，其中分析模型Ⅱ减小更多；2)工况6的跨中节点的峰值加速度减小的比例最大，减小了22.51%，工况5的跨中节点的峰值加速度则略微增加了0.138%。

各工况下钢连廊前三阶频率 表5

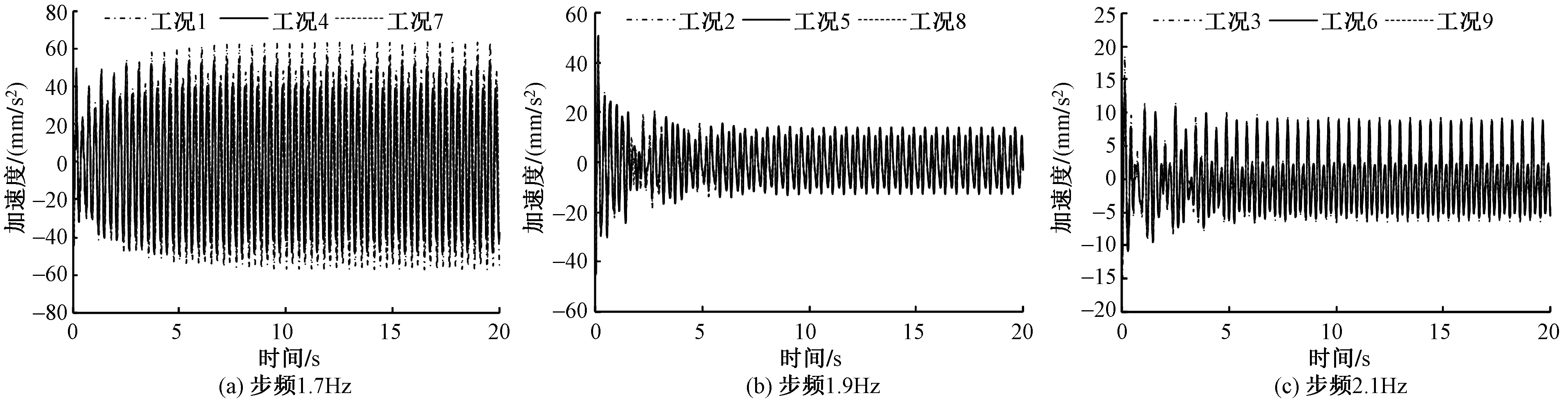
图10 各工况下钢连廊跨中节点加速度时程曲线

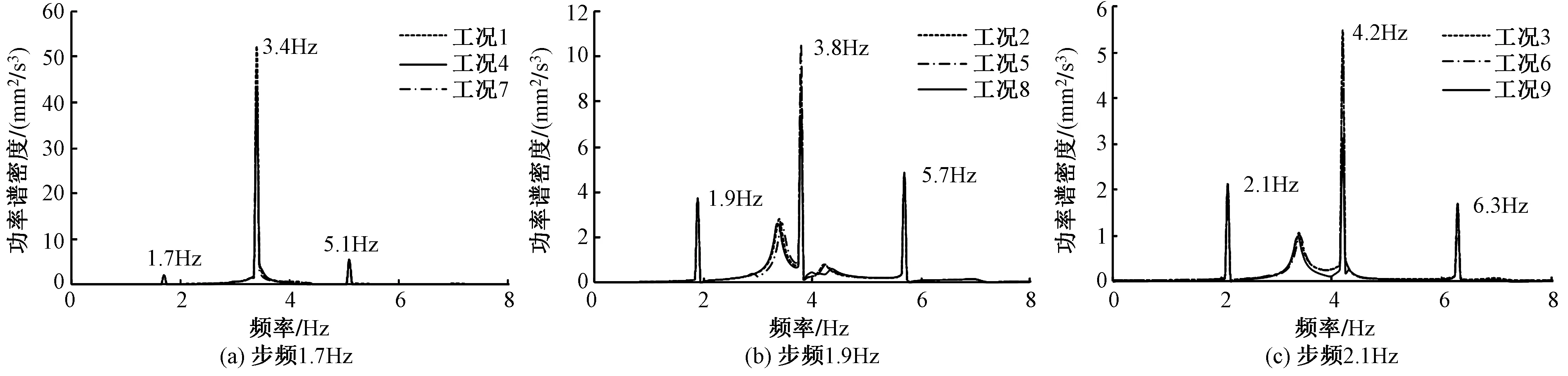
图11 各工况下钢连廊跨中节点加速度功率谱密度

图9 各工况下钢连廊跨中节点峰值加速度

图10给出了各工况下钢连廊跨中节点加速度时程，对比可知：1)1.7Hz人群荷载作用下的时程曲线的阻尼衰减效应相对于其余两个频率的工况不明显，结合图11(a)可知1.7Hz人群荷载的第2阶谐波与结构第1阶竖向模态发生共振；2)无论何种工况的时程曲线均呈现出显著的高阶谐波影响，因此，在进行人群荷载模拟时，步行曲线的高阶项不可忽略。

图11为各工况下钢连廊跨中节点加速度功率谱密度，对比可知：1)对于该连廊，响应受步行曲线的第2阶项影响最大，即在步频的2倍频处响应能量最大；2)在步频为1.9Hz时(图11(b))，考虑人-钢连廊耦合作用的工况5下钢连廊跨中节点峰值加速度却略有增加，工况8的峰值加速度减小比例非常小，可见对于本文分析的钢连廊而言，在非共振频率下，考虑人-结构耦合作用可能会引起钢连廊的动力响应略微增大；3)行人步频为1.7Hz和1.9Hz时人群密度均为1.0m/s2，步频为2.1Hz时人群密度为0.5m/s2，结合图4可知，单个行人的步频越高产生的动力荷载越大，但是人群密度减小，因此人群密度并不直接影响结构的峰值加速度减小的比例，人群密度的变化使得耦合的MSD模型的数量以及行人的步频发生变化，从而使整个耦合系统的质量、阻尼、刚度在不同人群密度下所表现出的结构的动力特性及动力响应不同。

4 钢连廊舒适度评价

舒适度评价指标有多种形式，如频率限值标准、加速度限值标准、均方根加速度限值标准等。由于人对结构振动的反应存在很大的主观性和不确定性，受到很多因素的影响，具有很大的差异性，所以目前国内外没有统一的标准。我国的《建筑楼盖结构振动舒适度技术规范(征求意见稿)》[17]中明确提出了对连廊的振动舒适度的要求，规定连廊和室内天桥的第1阶竖向自振频率不宜小于 3.0Hz，第1阶横向自振频率不宜小于 1.20Hz，连廊和室内天桥的振动峰值加速度不应大于表6的限值。

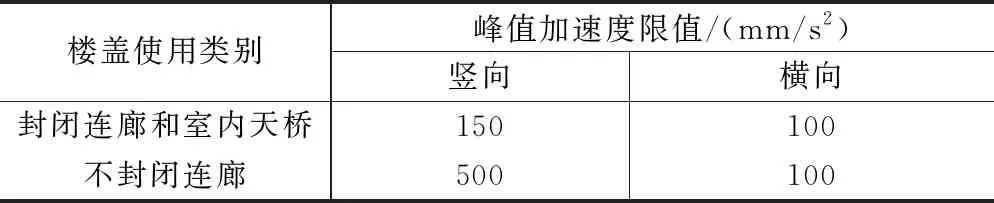
连廊和室内天桥的振动峰值加速度限值 表6

本文研究的室内大跨连廊的第1阶竖向自振频率3.39Hz略大于《建筑楼盖结构振动舒适度技术规范(征求意见稿)》[17]中规定的3.0Hz，第1阶横向振动频率2.01Hz大于规定的1.20Hz，满足频率限值要求。该连廊在不考虑人-结构耦合作用时的最大峰值加速度为63.68mm/s2，考虑人-结构耦合作用时的最大峰值加速度为52.61mm/s2，均小于规范中的150mm/s2，满足规范要求。因此该大跨钢连廊满足舒适度要求。

5 结论

围绕人-结构耦合振动对大跨度钢连廊振动舒适度分析结果的影响展开研究，从人-结构耦合作用模型、钢连廊人群荷载模拟和耦合作用影响规律等方面展开研究，得到以下结论：

(1)人-结构耦合作用对结构动力特性影响主要取决于结构人群密度，人群密度大，影响越大，人群密度小，影响越小。对于本文的钢连廊，由于人群质量远小于结构质量，动力特性影响相对较小，频率最大变化仅有5.06%。

(2)对于大跨钢连廊，考虑人-结构耦合作用后，工况5结构竖向加速度略微增加，其余工况加速度响应均减小，最大减小比例发生于步频2.1Hz时，达到22.51%。

(3)本文研究的大跨钢连廊在考虑和不考虑人-结构耦合作用下，第1阶竖向自振频率均大于3.0Hz，各工况下峰值加速度均小于规范中150mm/s2，满足人致振动舒适度要求。