某采用摩擦摆隔震支座的钢筋混凝土框架结构设计与分析

杨忠平， 雷远德， 邓 烜， 郁银泉， 李戚齐

(1 甘肃省工程设计研究院有限责任公司， 兰州 730030；2 中国建筑标准设计研究院有限公司， 北京 100048)

0 引言

隔震技术作为目前世界上最有效的建筑防震技术之一，在多个国家得到了广泛应用。隔震技术的原理为在建筑基础、底部或下部结构与上部结构之间设置隔震支座和阻尼装置等部件，组成具有整体复位功能的隔震层，以延长整个结构体系的自振周期，减少输入上部结构的水平地震作用[1]。一般来说，采用隔震技术之后上部结构结构的自振周期延长2～3倍以上，能够取得较好的隔震效果。因此，隔震支座作为隔震建筑中最重要的力学功能构件，应当具有较大的竖向承载力和竖向刚度、较小的水平刚度和较大的水平变形能力。我国的建筑隔震技术发展与橡胶支座的应用具有密切的关系，现有建筑隔震技术标准[1-2]中也仅对橡胶隔震支座进行了相关参数的规定。

摩擦摆隔震支座作为一种支座主体为钢材的刚性滑动隔震支座，自20世纪80年代美国加州大学Zayas等[3]提出以来在工程中开始了广泛应用，主要包括建筑、桥梁、天然气储罐等，相关产品技术也与橡胶支座一起被列入常用的隔震支座种类中[4-7]。在我国桥梁工程领域，摩擦摆隔震支座作为一种重要的隔震支座类型在大量重要工程得以应用[8-9]，并形成了相关标准[10-11]。该支座在自复位能力、隔震周期、抗扭能力、耐久性等方面具有显著优势，近年来在国内建筑领域得到了广泛关注，并编制了相应的产品标准[12]。本文以一个基础隔震工程为例，介绍建筑摩擦摆隔震设计的特点。

1 工程概况

本工程为某职业中等专业学校教学楼项目。建筑面积为6 237.72m2，占地面积为1 025.20m2，建筑高度为23.70m，高宽比为1.275；建筑长度为54.40m(包括建筑外皮)，建筑宽度为18.70m，室内外高差为0.30m，房屋高度为27.60m。地上6层。工程建筑平面布置和立面分别如图1和图2所示。工程建筑抗震设防类别为重点设防类(乙类)建筑。

本工程为钢筋混凝土框架结构，采用基础隔震，隔震层及其以下结构抗震等级为一级，隔震层以上结构抗震等级为二级。抗震设防烈度为8度，设计基本地震动加速度为0.20g；设计地震分组为第二组，场地类别为Ⅱ类场地，场地特征周期为0.40s；抗震设防类别为重点设防类(乙类)。采用《建筑抗震设计规范》(GB 50011—2010)[1](简称抗规)中的隔震设计方法进行设计，其中时程分析时多遇地震下加速度峰值为70gal，设防地震下加速度峰值为200gal，罕遇地震下加速度峰值为400gal。

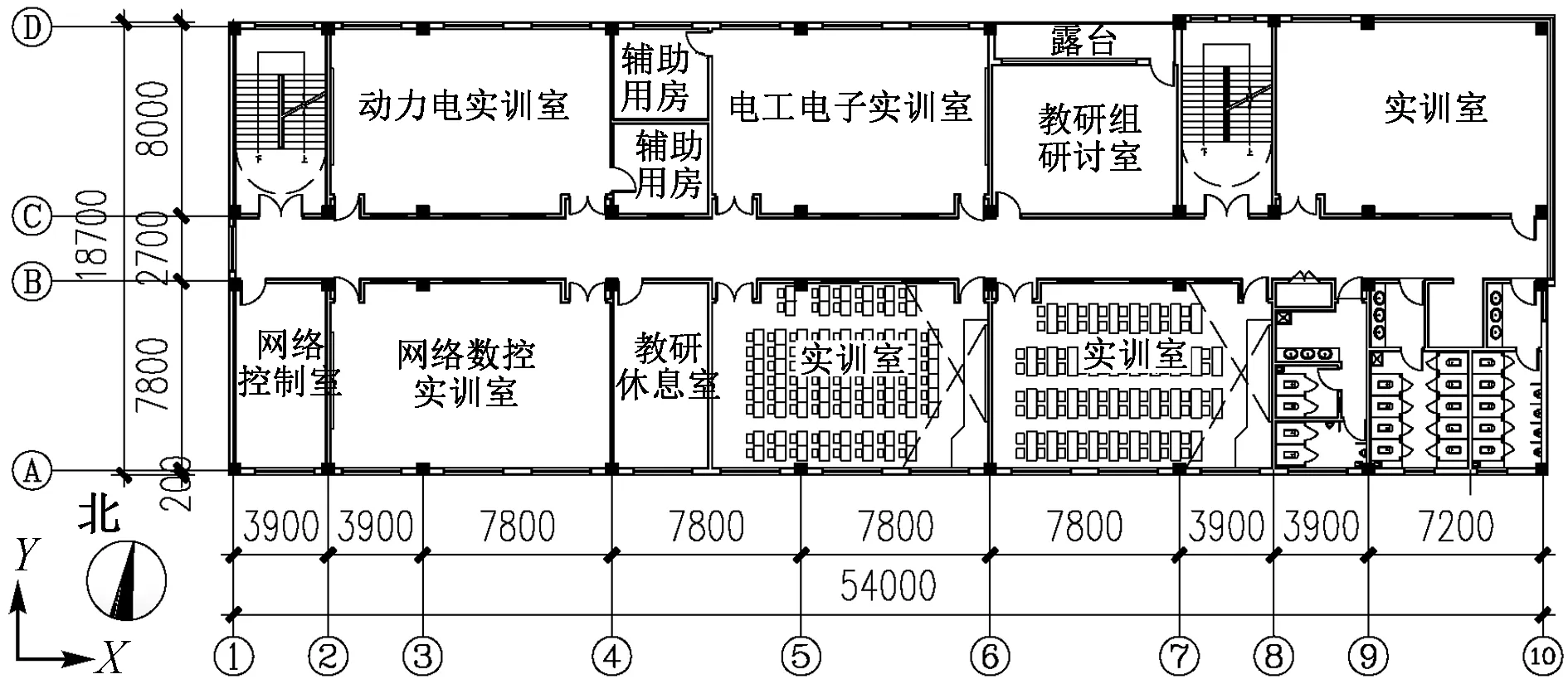
图1 2层建筑平面布置图

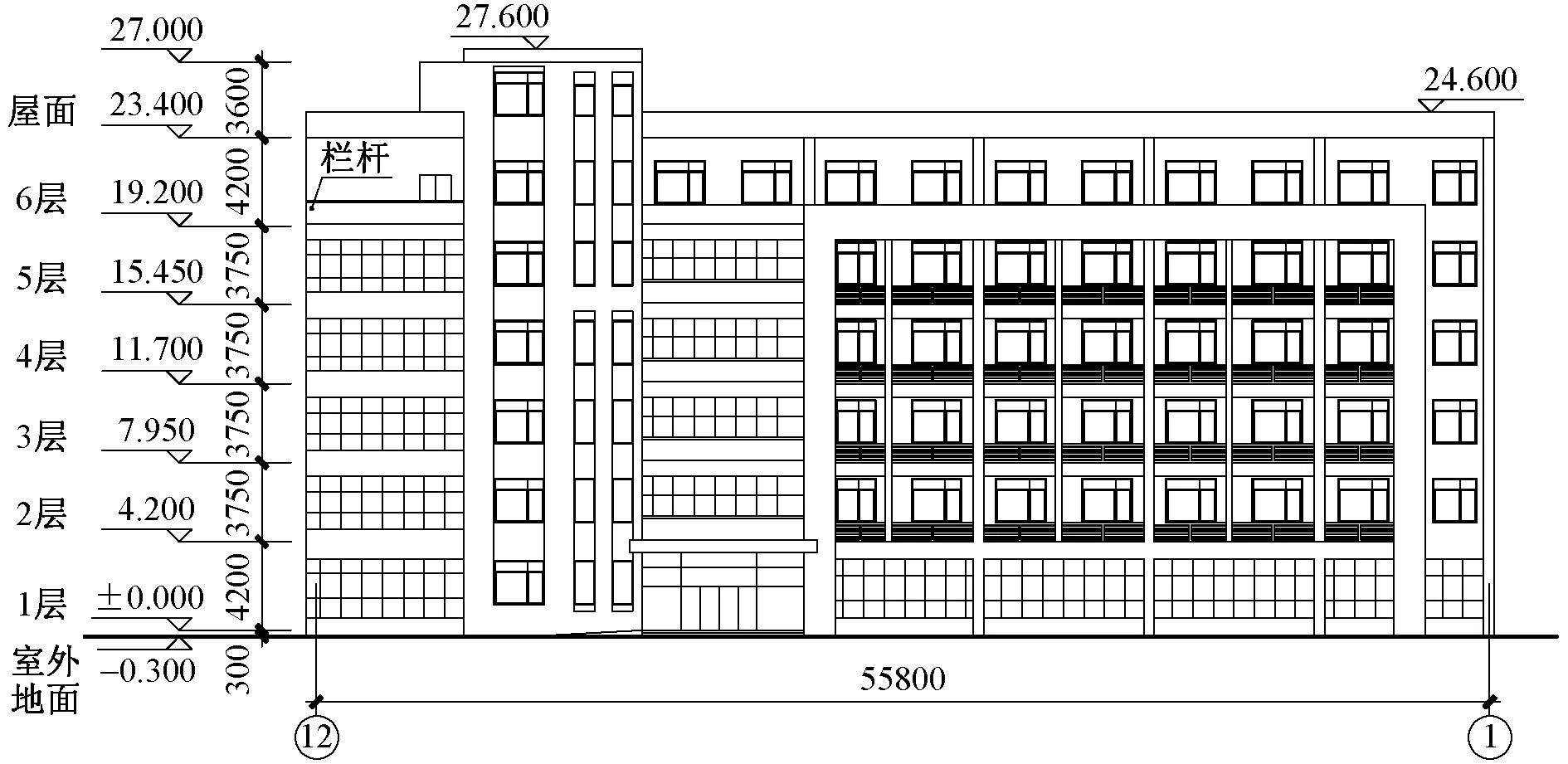
图2 建筑立面图

2 摩擦摆隔震支座

2.1 力学性能指标

摩擦摆隔震支座属于滑动支座，其示意图如图3所示。其中，R为支座等效曲率半径；R1为支座下滑动摩擦面曲率半径；R2为支座上滑动摩擦面曲率半径；d为球冠体中间高度。

图3 摩擦摆隔震支座示意图

摩擦摆隔震支座为非线性单元，为了简化分析，其滞回力学模型可采用双线性模型，如图4所示，其中Kc为屈服后刚度。支座的初始刚度Kp、等效刚度Keff和水平恢复力F分别按式(1)，(2)和(3)计算。

(1)

(2)

(3)

式中：μ为动摩擦系数；P为支座所受竖向荷载；dy为屈服位移，一般取2.5mm；D为支座水平位移。

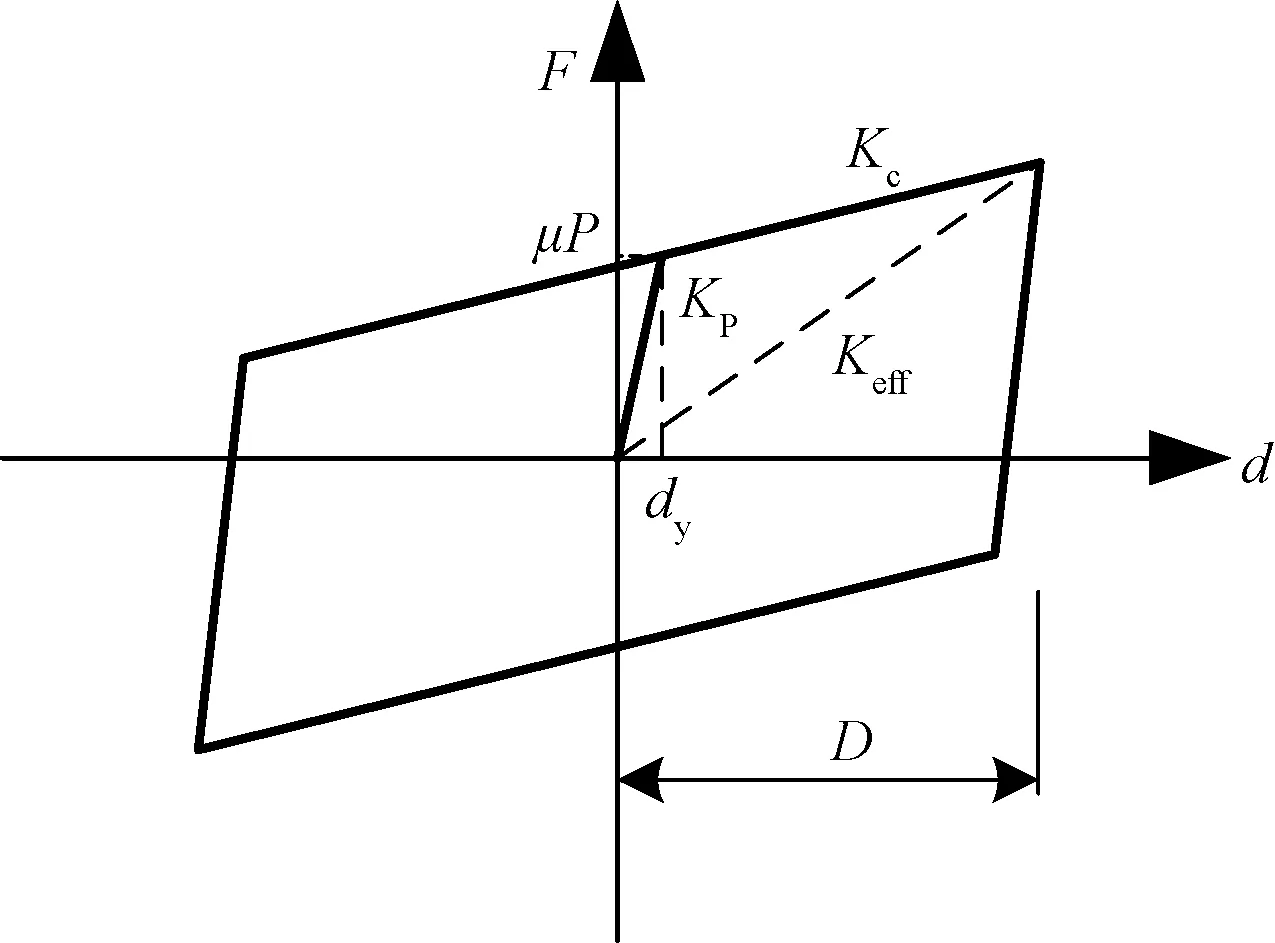
图4 摩擦摆隔震支座的荷载-位移滞回曲线

其中PTFE等黏弹性材料的动摩擦系数μ被认为是与压应力和相对速度相关的，摩擦系数可采用式(4)进行参数化表达。而在现有的商业通用有限元软件中摩擦摆隔震支座的摩擦系数忽略了压应力相关性，表达式见式(5)。

μ(v,σ)=[μfast-(μfast-μslow)ge-αv]·σ-β

(4)

μ(v)=μfast-(μfast-μslow)·e-αv

(5)

式中：μfast为快速动摩擦系数；μslow为慢速动摩擦系数；α为比率参数；v为滑动相对速度；σ为压应力，MPa；β为压应力相关性系数。

2.2 摩擦摆隔震支座布置

根据重力荷载代表值作用下的柱下反力在隔震层中合理布置摩擦摆隔震支座，摩擦摆隔震支座的布置和选型见图5，摩擦摆隔震支座参数见表1。摩擦摆隔震支座的长期面压考虑控制重力荷载代表值作用下的支座受压应力，其荷载组合为1.0恒载+0.5活载。

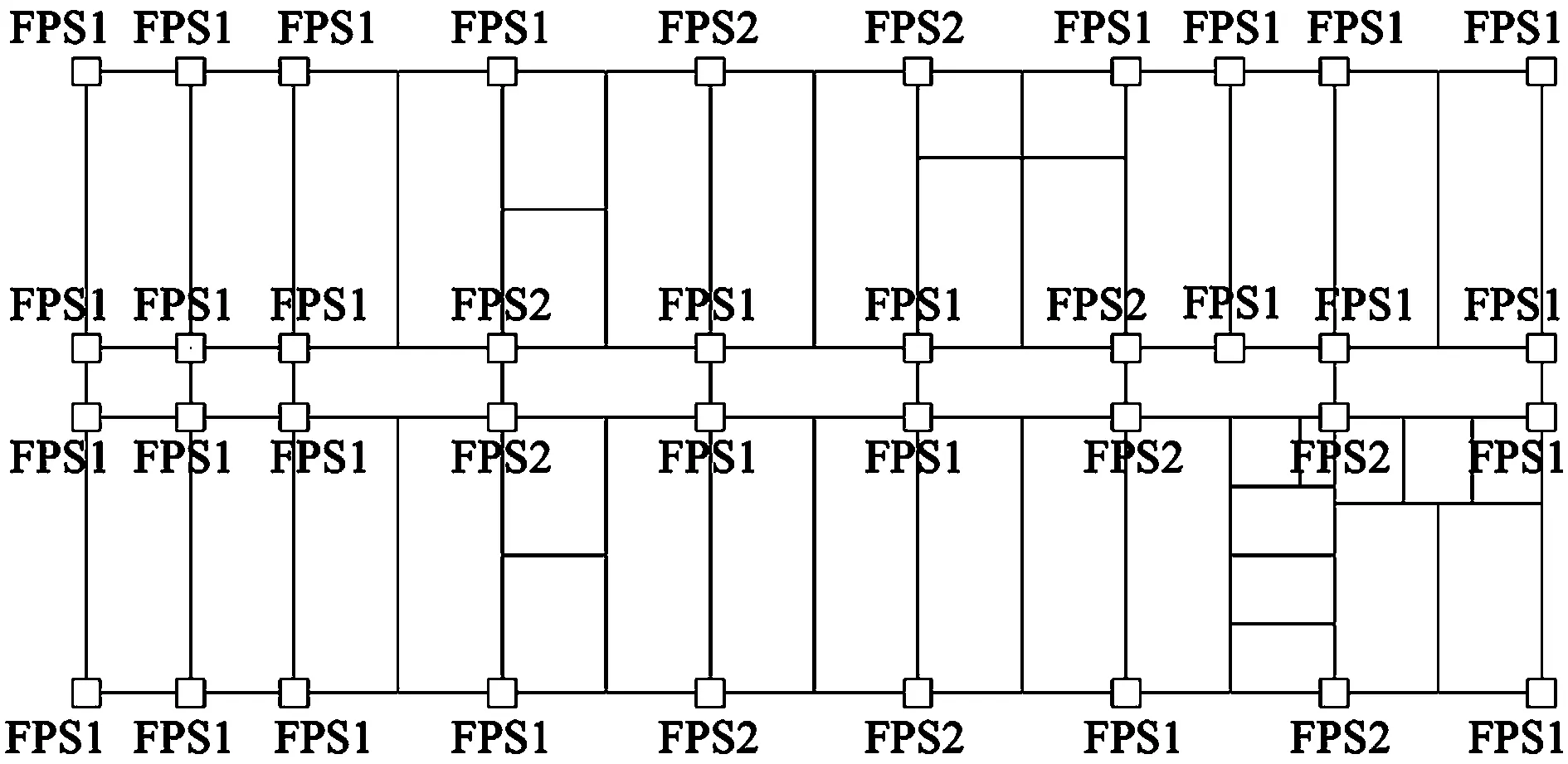
图5 摩擦摆隔震支座平面布置图

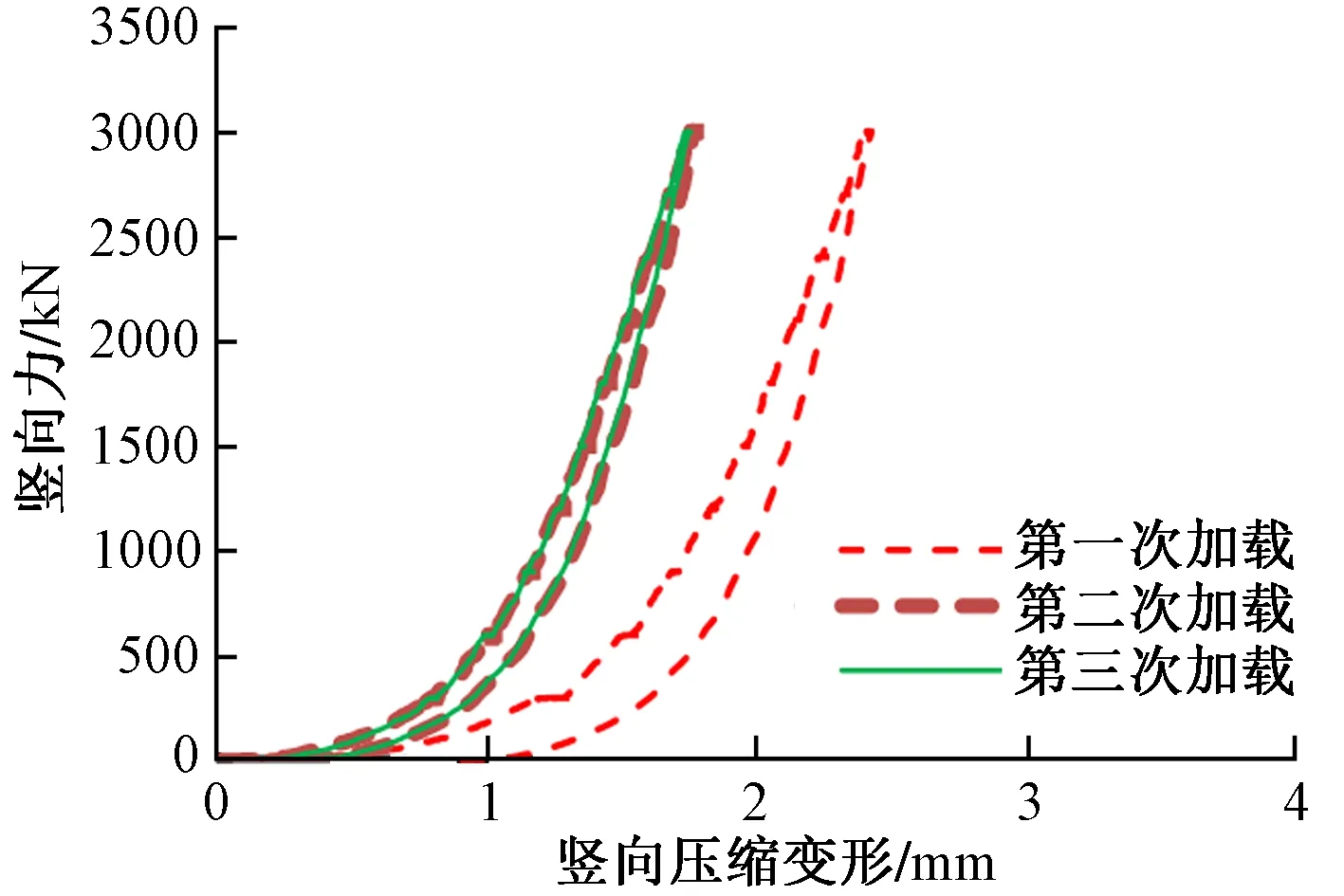
图6 摩擦摆隔震支座竖向压缩变形

图7 摩擦摆隔震支座摩擦系数试验测试结果

图8 隔震结构有限元模型

根据文献[4]和欧洲规范EN 1337-2∶2004[7]，摩擦摆隔震支座在重力荷载代表值作用下的压应力不应大于24MPa，根据承压形式相近的《橡胶支座 第5部分：建筑隔震弹性滑板支座》(GB 20688.5—2014)[13]规定，支座压应力不应大于25MPa。本项目支座的竖向面压分布集中于15～25MPa，最大支座面压为23.98MPa，说明隔震层具有足够的稳定性和安全性。

摩擦摆隔震支座参数 表1

2.3 隔震支座试验结果

依据《建筑摩擦摆隔震支座》(GB/T 37358—2019)[12]的相关要求，对摩擦摆隔震支座进行试验，这里仅取一个FPS1支座竖向压缩变形和摩擦系数的检测结果进行说明。

摩擦摆隔震支座竖向压缩变形见图6。由图可见支座竖向变形均值为1.89mm，在完成预压之后的支座竖向变形均值在1.60左右，支座竖向刚度与设计参数的误差小于10%。摩擦摆隔震支座摩擦系数试验测试结果见图7。测得动摩擦系数下限为0.016，动摩擦上限为0.033，与设计参数误差小于20%，试验结果与设计参数吻合性较好。

3 有限元模型验证及地震波选取分析

3.1 有限元模型

采用ETABS软件建立了隔震结构和非隔震结构的三维有限元模型，具体见图8。梁、柱构件采用空间杆系单元，楼板采用壳单元。隔震模型中，增设隔震支座(摩擦摆隔震支座采用连接单元Isolator2[14])。

隔震结构的动力特性会随着隔震支座水平变形的变化而不断变化，这里隔震支座的等效水平刚度取支座中震作用下的隔震层位移对应的等效刚度。在ETABS软件中利用Ritz向量法计算出非隔震结构和隔震结构前30阶动力特征，前6阶振型周期如表2所示。可以看出，隔震结构的周期较非隔震结构增大很多，基本周期由原来的1.13s延长至2.63s。

非隔震结构和隔震结构前6阶周期/s 表2

3.2 设计地震波的选取

根据抗规的相关规定，选取了7条地震波(5条天然波TR1～TR5和2条人工波RG1～RG2)对非隔震结构模型和隔震结构模型进行时程分析，取7条波时程法的平均值作为最终的计算结果。7条波的平均反应谱与规范谱的比较如图9所示。在隔震结构与非隔震结构第一周期点附近二者较接近。

3.3 设计地震波地震剪力分析

表3和表4分别给出了非隔震结构在多遇地震作用下各楼层基底剪力的时程分析和反应谱分析的结果。计算分析得出，每条时程曲线计算得到的弹性非隔震结构的基底剪力均大于反应谱计算结果的65%，且不大于反应谱结果的135%；7组时程曲线计算所得结构基底剪力的平均值大于反应谱法计算结果的80%，且时程结果不大于反应谱结果的120%，均满足规范要求。采用7组时程曲线作用下最大地震响应值的平均值作为时程分析的最终计算值，结果可以用于工程设计。

多遇地震基底剪力时程分析结果/kN 表3

多遇地震基底剪力反应谱分析结果/kN 表4

3.4 摩擦系数压应力相关性的影响评估

在ETABS软件中，摩擦摆隔震支座参数不考虑压应力的相关性，为评估这种忽略带来的的计算误差，在ABAQUS软件中进行子程序的二次开发，利用Vuel单元开发出分别按照式(4)和式(5)的摩擦摆隔震支座单元，分析忽略压应力计算结果的误差。计算模型见图10，其中计算地震水准取罕遇地震水准。取其中一条人工波的计算结果，见图11。

计算结果表明：在考虑压应力相关性的情况下，隔震层的竖向力与水平剪力时程均与不考虑压应力的情况基本一致，计算结果偏小，误差在5%以内；角部支座作为受竖向力变化影响最大的支座，考虑压应力变化的情况，竖向力与水平力均较不考虑的情况偏小，误差在20%以内。由此可以简单判定，采用不考虑压应力的摩擦摆隔震支座模型计算结果是偏于安全的，且隔震层整体计算结果精度较高，误差在工程可接受的范围内。

图9 地震波反应谱与规范谱比较

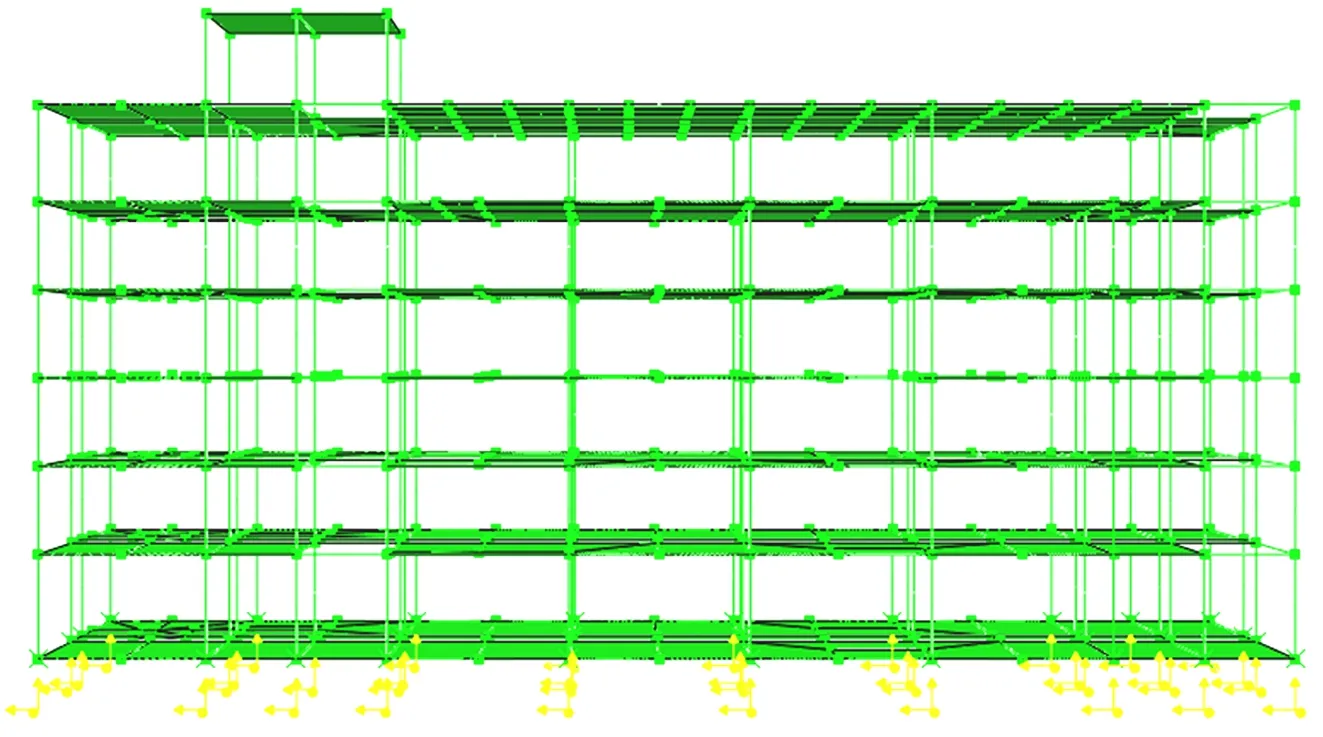
图10 ABAQUS软件计算验证模型

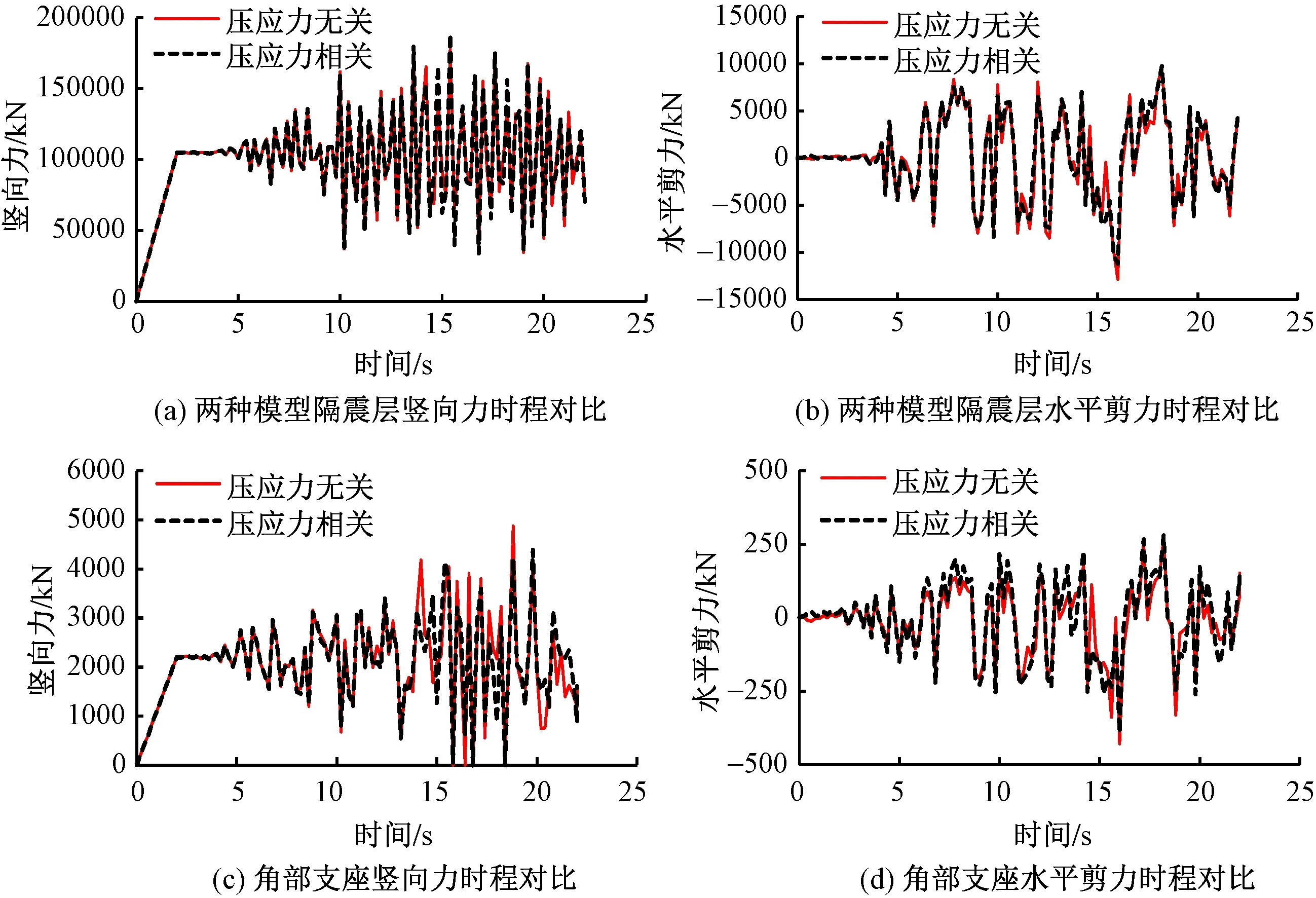
图11 ABAQUS验证对比结果

4 隔震层验算

4.1 抗风验算

风荷载作用下隔震层不应发生水平位移[2,15]，需对隔震层进行抗风验算，具体验算公式如下：

γwVwk≤VRw

(6)

式中：VRw为抗风装置的水平承载力设计值；γw为风荷载分项系数，取1.4；Vwk为50年一遇风荷载作用下隔震层的水平剪力标准值。

其中隔震层的本构模型可简化为双折性模型(参见图4)，两段的计算公式如下：

VRW=μfastGeq

(7)

(8)

式中：VRw为隔震层的屈服承载力；μfast为快速动摩擦系数；Geq为结构重力荷载代表值；Kc为屈服后刚度；R为支座等效曲率半径。

本工程隔震层的水平力恢复特性如图12所示。可以看出，隔震层的屈服承载力大于1.4倍的50年一遇风荷载下的隔震层剪力，因此隔震层满足抗风要求。

4.2 设防地震作用下减震系数

分析了非隔震结构和隔震结构在设防地震(8度0.20g)作用下的楼层剪力，并计算了不同地震波作用下隔震结构的减震系数，结果如图13所示。

由图13可以看出，隔震结构在8度设防地震作用下，X向地震剪力最大值为非隔震结构的0.407，Y向地震剪力最大值为非隔震结构的0.396，总体平均值为0.365，这表明所设计的隔震系统具有良好的隔震效果。本工程隔震结构的减震系数可取0.365。

4.3 设防地震作用下层间位移角

在设防地震作用下隔震结构的上部结构的层间位移角曲线如图14所示。在设防地震作用下隔震结构最大层间位移角为1/533，基本保持弹性，结构安全储备充足。

4.4 罕遇地震作用下隔震层位移

罕遇地震作用下隔震层最大位移如表5所示。上部结构按照弹性计算的隔震层最大位移为255mm，满足规范要求。由于摩擦摆隔震支座的水平力学性能与上部荷载呈线性关系，因此在地震荷载作用下，摩擦摆隔震支座能够随着上部结构地震作用力的变化而实时调整，时刻保持隔震层部位质心与刚心大致重合。本项目各摩擦摆隔震支座在地震作用下的最大位移见图15。隔震层支座位移基本相同，隔震层最大位移比为1.03，隔震层及上部结构的扭转变形很小。

罕遇地震下隔震层最大位移/mm 表5

4.5 罕遇地震作用下的层间位移角

罕遇地震作用下隔震结构的层间位移角如图16所示。罕遇地震作用下，隔震结构最大层间位移角为1/350，远小于我国抗规中规定的1/50，满足规范要求，具有较大的安全储备。

4.6 罕遇地震作用下支座反力

罕遇地震作用下的极值面压需考虑重力荷载代表值、罕遇地震作用下的水平地震作用和竖向地震作用，在本结构模型中通过直接施加重力荷载作用下的大震时程分析结果进行校验。计算结果表明，结构在罕遇地震下的最大支座压力为3 075kN，压应力为38.2MPa，发生在短跨跨中位置；最小压应力为0.2MPa，发生在角部位置。

5 与叠层橡胶隔震支座隔震方案的对比分析

5.1 叠层橡胶隔震支座布置及隔震层本构

为与叠层橡胶隔震支座隔震方案进行对比，针对本项目进行了相应叠层橡胶隔震支座隔震设计，叠层橡胶隔震支座布置见图17，叠层橡胶隔震支座力学参数见表6，隔震层本构对比见图18。由图18可见叠层橡胶隔震支座与摩擦摆隔震支座在中震作用下的隔震层恢复力大致相近，但是摩擦摆隔震支座方案的屈服力大、屈服后刚度小。叠层橡胶隔震支座方案的隔震结构周期为2.83s，结构减震系数为0.390，隔震层最大位移为238mm，计算结果与摩擦摆隔震支座方案相近。

图12 隔震层水平力恢复特性

图13 隔震结构的减震系数

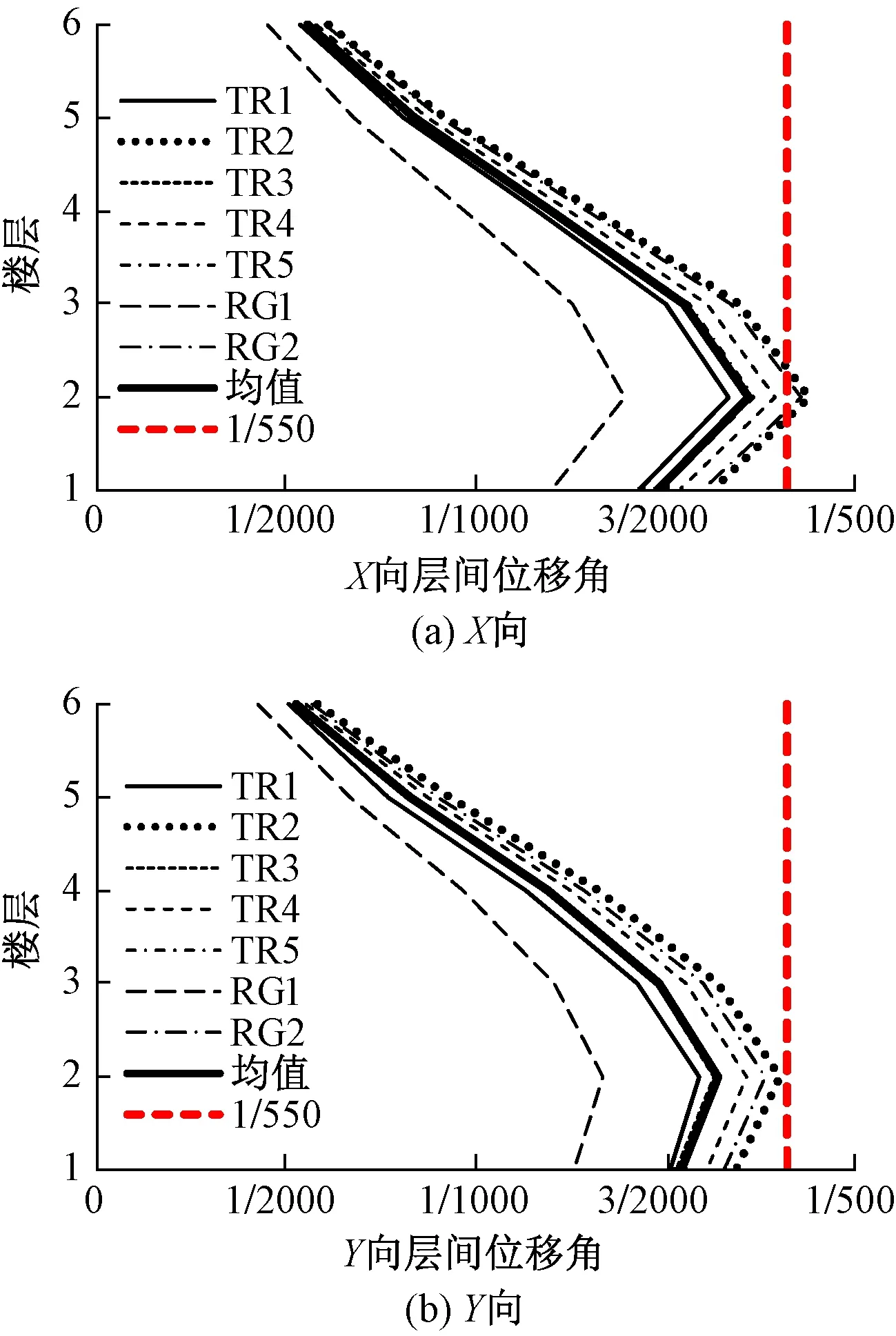
图14 设防地震作用下隔震结构的层间位移角

图15 罕遇地震作用下各个支座的最大位移

图16 罕遇地震作用下隔震结构的层间位移角

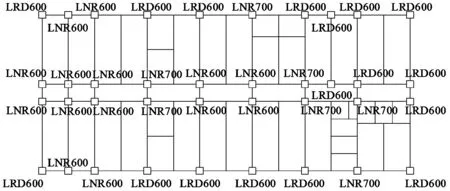
图17 叠层橡胶隔震支座布置方案

叠层橡胶隔震支座力学参数 表6

图18 隔震层本构对比

5.2 隔震层扭转反应

叠层橡胶隔震支座布置方案需要控制隔震层支座的刚度中心与质量中心重合，在本项目中叠层橡胶隔震支座隔震层刚度中心与质量中心的偏心率小于3%。

通过时程分析选取3条隔震层扭转较为显著的地震波作用下叠层橡胶隔震支座位移与摩擦摆隔震支座方案进行对比，具体见表7。结果表明，叠层橡胶隔震支座方案隔震层位移比为27.18%，摩擦摆隔震支座方案隔震层位移比为3.00%，摩擦摆隔震支座在控制结构扭转方面具有显著优势。

隔震层扭转反应对比 表7

5.3 隔震支座的连接

隔震支座的上下连接板分别与上下结构通过螺栓连接，该螺栓连接应该采用可拆换的外插入螺栓连接方案，如图19所示。所有连接螺栓或锚固钢筋，均按罕遇地震作用下产生的水平剪力、弯矩进行强度验算。

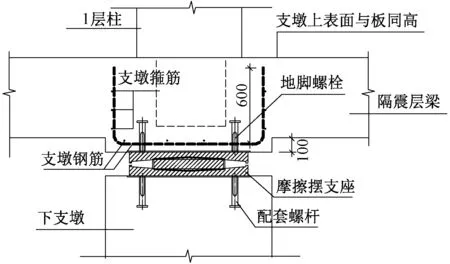
图19 隔震支座上下连接示意图

当采用叠层橡胶隔震支座方案时，叠层橡胶隔震支座的连接螺栓需要计算在偏心受压弯矩下的拉力[16]。此时计算得LRB600叠层橡胶隔震支座的螺栓锚固长度应为450mm。

而摩擦摆隔震支座具有和叠层橡胶隔震支座不同的受力机制，支座构造及下座板受力分析图见图20，其中近似认为竖向力和水平力均经过球冠板正中。当考虑罕遇地震作用下支座下座板受摩擦力f和竖向力N的共同作用时，其受力平衡见式(9)。

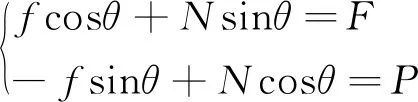
(9)

其中：

可得水平恢复力F与竖向压力P关系：

(10)

考虑绕O点逆时针方向转动的弯矩见式(11)，即支座不会产生逆时针方向的转动，连接螺栓不受拉。螺栓预埋件考虑最小构造长度即可，根据抗规取250mm。

MO=Fh-P(r-d)<0

(11)

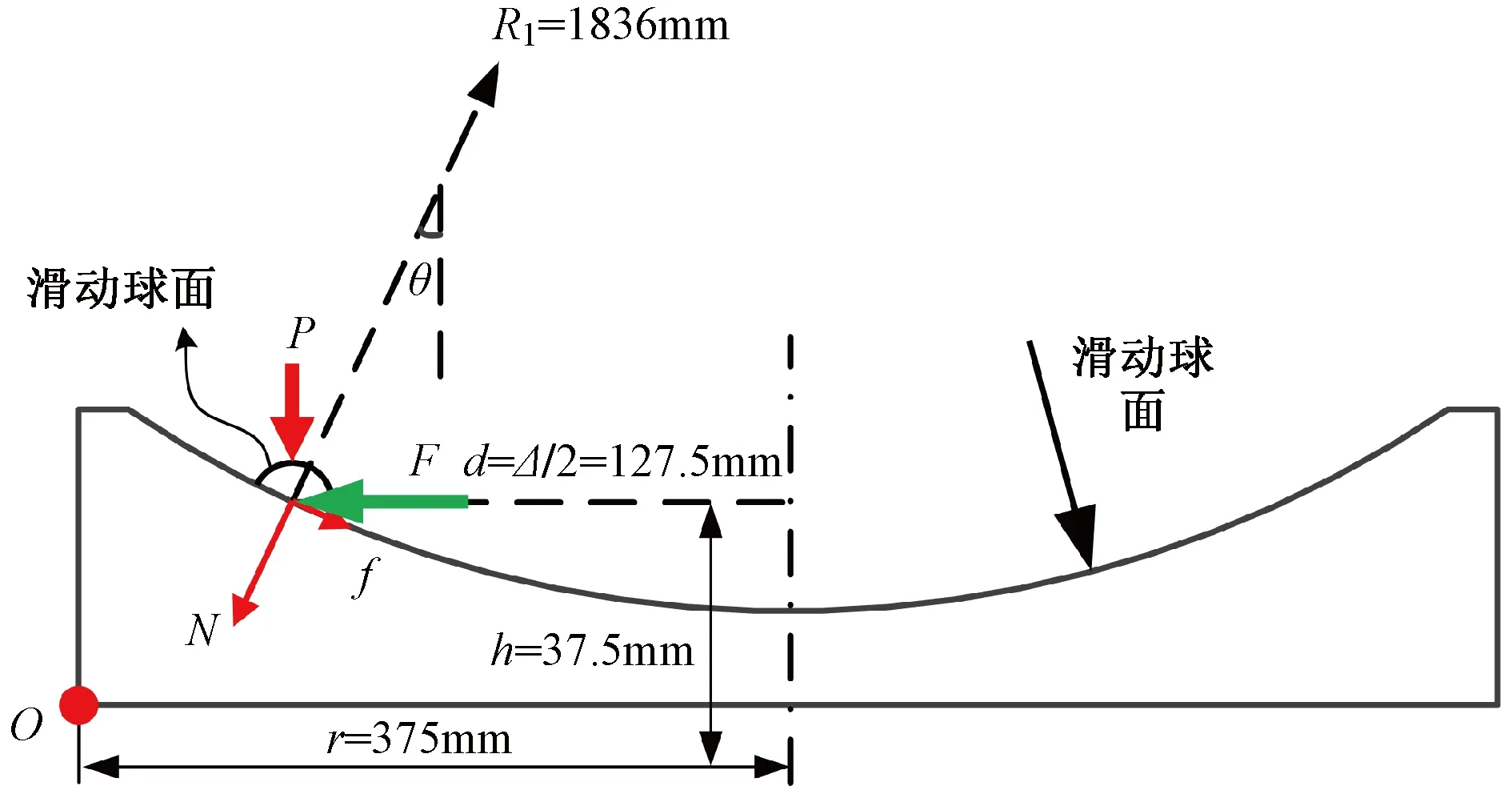
图20 FPS1摩擦摆隔震支座下座板受力简图

6 结论

本文通过对一个钢筋混凝土框架结构工程采用摩擦摆隔震支座隔震方案进行了设计与分析，并与普通橡胶隔震支座方案进行了对比，得到以下结论：

(1)利用ETABS软件考虑支座非线性特性的时程分析能够有效模拟摩擦摆隔震支座的在地震作用下的反应，隔震支座的试验结果与数值模拟参数吻合度较高。

(2)根据抗规的设计方法，采用摩擦摆隔震支座能够有效地减小建筑结构的地震反应，能够实现与普通橡胶隔震支座相同的隔震效果。

(3)摩擦摆隔震支座的隔震层水平刚度中心与上部结构的竖向作用力呈正相关关系，在地震作用下隔震层处的质心与刚心重合度较高，能够有效抑制结构的整体扭转，与叠层橡胶隔震支座相比具有显著优势。

(4)根据简化受力分析，罕遇地震作用下，摩擦摆隔震支座的连接螺栓不会出现受拉作用，在计算中仅需考虑水平受剪验算，螺栓预埋件长度仅满足构造长度即可，大大降低了支座安装难度。