采用BRB伸臂桁架的某超高层钢结构抗震性能分析*

陈 曦， 閤东东， 苏宇坤， 解琳琳， 伍炼红， 李文峰， 苗启松

(1 北京市建筑设计研究院有限公司， 北京 100045； 2 北京建筑大学土木与交通工程学院， 北京 100044)

0 引言

防屈曲支撑(BRB)由核心耗能段和外包约束构件构成，在轴力作用下发生全截面屈服，在拉伸和压缩方向受力性能对称，具有变形能力强、刚度大、滞回性能好、拉压承载稳定性好、减震机理明确和减震效果明显的特点，可以满足不同结构的抗震要求[1]。在正常使用状态及小震作用下，BRB为建筑结构提供抗侧刚度，起到普通支撑的作用；在罕遇地震作用下，BRB可通过其反复拉压屈服耗散地震输入的能量。超高层建筑随着结构高度的增加，由于整体弯曲变形的影响，上部楼层有害位移角所占比重逐层减小，导致上部楼层中的BRB有效变形减少，耗能效果有限。超高层建筑通常采用伸臂桁架协调核心筒和外框架之间的受力，使外框架承担更多的倾覆力矩[2]。伸臂桁架的刚度大、屈服后对整体结构竖向安全性影响小，在地震作用下是理想的耗能部位，因此将伸臂桁架中的普通钢支撑斜腹杆置换成BRB可取得良好的减震效果。蒋庆等[2]以高度为230.9m的某超高层建筑为研究对象，通过弹塑性时程分析对采用普通伸臂桁架和BRB伸臂桁架的高层建筑耗能机制进行对比研究，发现BRB伸臂桁架较普通伸臂桁架具有更好的变形能力和耗能能力。袁林华等[3]和周忠发等[4]在乌鲁木齐宝能城项目中，在结构关键部位设置了屈服力达15 000kN的BRB。杨青顺等[5]对设置BRB的耗能伸臂桁架进行了试验研究。武莲霞等[6]将耗能型BRB和承载型BRB在伸臂桁架中混合使用，使结构刚度分布更加合理，解决结构的扭转问题。Lin等[7]将BRB用于伸臂桁架中，有效地降低了建筑物的地震反应。

本文所述的某超高层钢结构项目共设置了863根普通钢支撑，并在结构底部加强区和伸臂桁架腹杆处设置了104根BRB，属于超限高层建筑结构。本文采用动力弹塑性时程分析方法对结构抗震性能进行评估，研究结构在罕遇地震作用下的变形模式和塑性发展状况及关键构件变形形态和破坏情况。

1 工程概况

1.1 结构概况

本工程位于乌鲁木齐市，建筑功能为公寓，结构高度为280m，结构地上69层，地下3层，标准层层高为3.85m，34层和58层均为避难层，层高分别为5.4m和4.5m。地上建筑面积约16.1万m2，结构平面为矩形，外轮廓尺寸为44m×52.4m，核心筒尺寸为28.1m×17m，基础埋深约22.8m。抗震设防烈度为8度，设计基本地震加速度为0.20g，设计地震分组为第二组，建筑场地类别为Ⅱ类，场地特征周期为0.40s。按避难层人数计算，建筑抗震设防类别为丙类。根据抗震设防类别和避让距离，还需对地震作用放大1.1倍。50年一遇基本风压0.60kN/m2，地面粗糙度类别为C类。地震作用下和风荷载作用下的阻尼比为0.02。

结构高度为280m，超过了规范高度限值260m，采用了内外筒方钢管混凝土框架-中心钢支撑(部分BRB)-伸臂桁架-环带桁架的结构体系。结构体系及伸臂和腰桁架布置如图1所示，在34层和58层共设置了2个加强层，其中34层和58层腰桁架钢支撑箱形截面分别为□450×450×30×30，□400×400×25×25。钢支撑主要截面包括□450×450×25×25，□400×400×25×25，□350×350×20×20和□300×300×18×18。

采用ABAQUS软件建立了结构的三维有限元模型，如图2所示。表1为计算得到的结构前6阶模态，结构第1, 2阶周期分别为7.60s和7.37s，振型分别为Y向和X向一阶平动。小震作用下结构X向和Y向最大层间位移角分别为1/325和1/333，X向和Y向最小剪重比均为2.2%。

各构件抗震设计性能目标如下：设防地震作用下，与钢支撑相连的框架柱要求抗弯不屈服、抗剪弹性，框架梁和BRB允许进入塑性，其余构件均要求抗弯不屈服和抗剪不屈服；罕遇地震下与支撑相连的框架柱要求抗剪不屈服，其余构件允许进入塑性。

1.2 消能减震方案设计

为提高结构底部加强区的耗能能力，保证关键构件的性能，将结构X向、Y向1～6层中心支撑置换为BRB，如图3所示。加强层与上下楼层存在较大的刚度突变，为减小加强层的刚度、减少刚度突变与内力剧增，加强层伸臂桁架的斜腹杆采用BRB。BRB参数如表2所示，其中BRB1和BRB2核心段强度等级为Q235B，BRB3～BRB6核心段强度等级为Q345B。

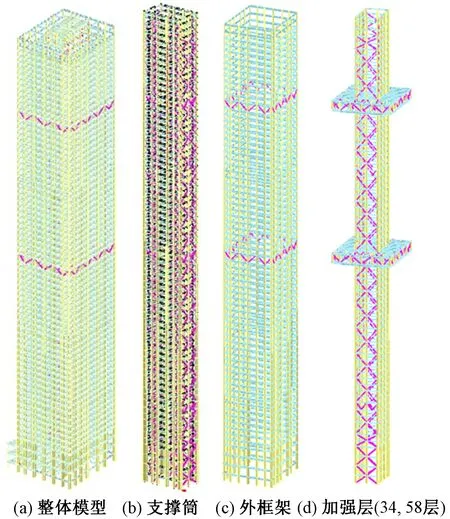
图1 项目结构体系

图2 结构有限元模型

图3 BRB布置示意

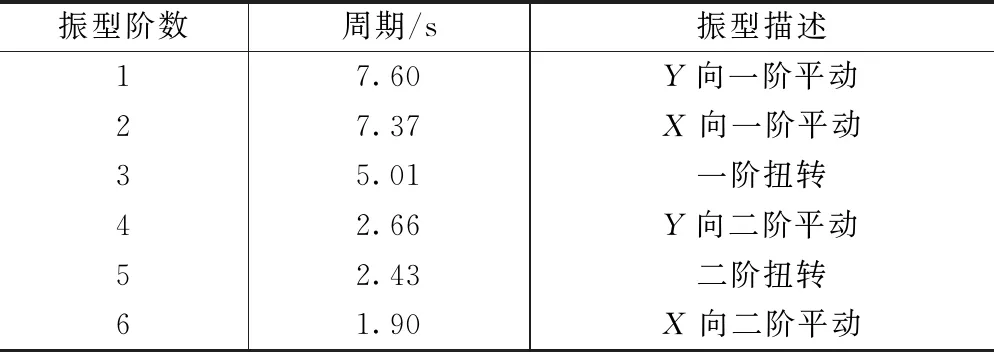
结构前6阶模态 表1

BRB参数 表2

2 普通钢支撑拉压不对称数值模拟

BRB中外约束套管可防止芯材发生整体屈曲，芯板在受拉和受压下均能进入屈服，变形能力强、滞回性能好。与BRB不同的是，普通钢支撑具有稳定的抗拉承载能力，但其受压时容易发生屈曲。BRB与普通钢支撑的滞回性能比较如图4所示。普通钢支撑的滞回特性包括稳定的受拉特性、受压时发生屈曲且屈曲荷载不断降低、受压卸载刚度逐渐降低等复杂拉压不对称现象，此现象对整体结构行为影响较大，有必要对其进行模拟。

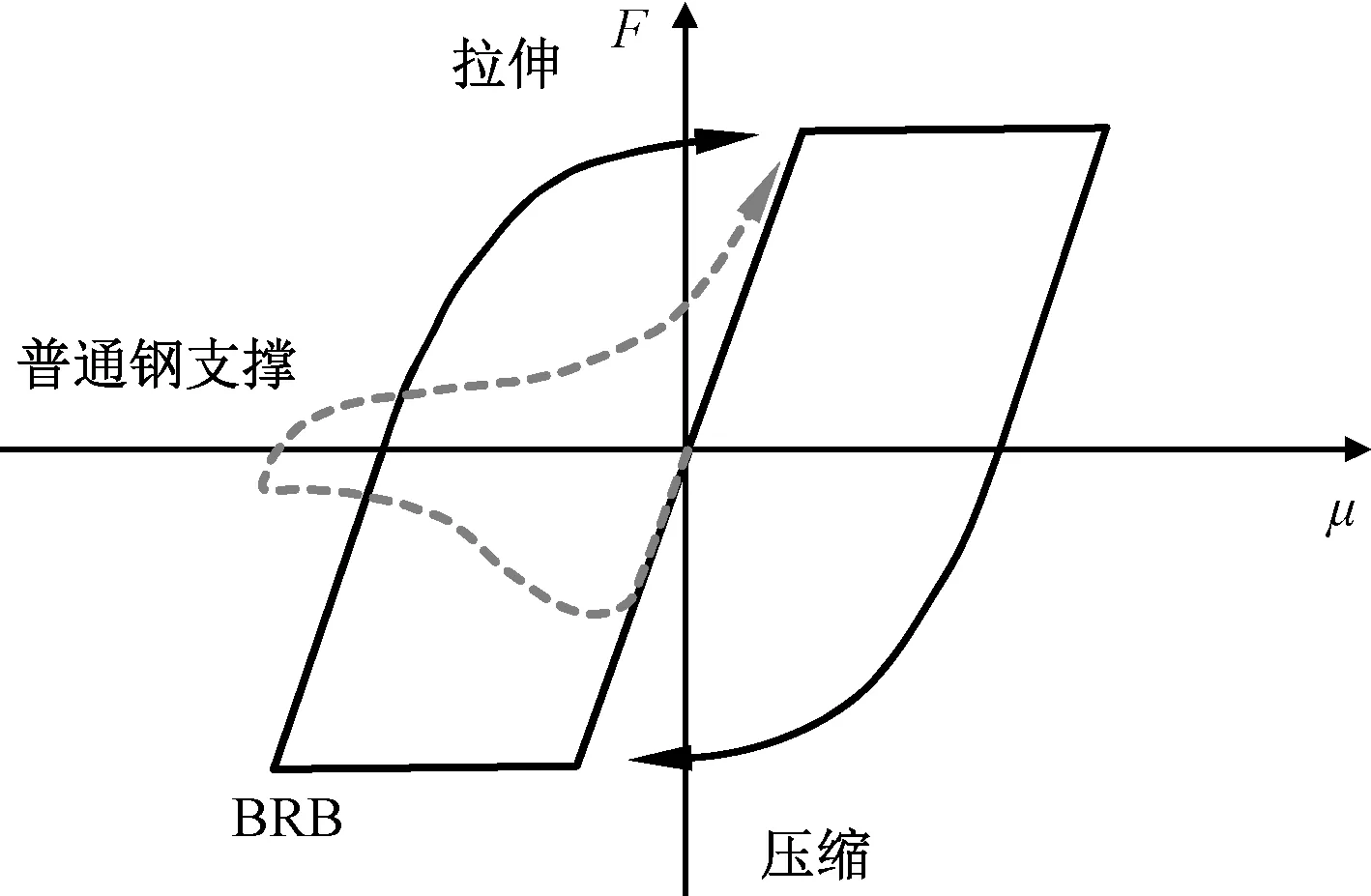
图4 BRB与普通钢支撑的滞回性能比较

图6 不同初始几何缺陷支撑的滞回曲线对比

2.1 普通钢支撑拉压不对称数值模拟方法

普通钢支撑滞回曲线的模拟方法主要有以下三种：现象描述法、塑性铰模型法和有限元法[8]。其中有限元法将支撑划分成离散的梁单元，赋予各单元各自的几何及材料特性，并在支撑中部设置初始几何缺陷来模拟支撑的滞回曲线。有限元法通用性强，模拟精度高，故本文采用有限元法。

2.2 考虑初始缺陷的有限元法数值模型分析

根据本工程实际情况，选取了长度为8m，截面为□650×650×36×36，□400×400×25×25和□100×100×20×20三种模型进行对比分析，钢材强度等级为Q345B，单元尺寸为1m，两端采用铰接约束。不同初始几何缺陷支撑的轴力及滞回曲线对比分析结果分别如图5和图6所示。

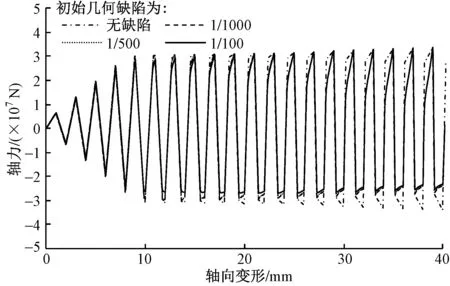
图5 不同初始几何缺陷支撑□650×650×36×36的轴力对比

结果显示初始几何缺陷对支撑初始轴力有较大影响，但对支撑整体的滞回曲线影响不大，钢支撑的长细比λ越大，初始几何缺陷导致支撑所受轴力下降越显著。因此，初始几何缺陷的取值仅会影响到支撑的初始轴力，对结构整体性能的影响并不大。考虑到国内目前钢结构的工艺水平，《钢结构工程施工质量验收规范》(GB 50205—2020)[9]规定钢支撑矫正后的允许偏差不应超过支撑长度的1/1 000。因此，分析中取钢支撑跨中的初始几何缺陷为1/1 000支撑长度，施加初始缺陷后每个钢支撑划分单元个数不小于8个。

3 地震波选择

根据规范要求，选取了3组地震波，包括天然波1、天然波2、人工波，每组地震波分别包含3个波，其反应谱曲线如图7所示。三组地震波持时、反应谱、产生的基底剪力均满足规范[10]要求。地震波输入时采用三向输入，水平双向与竖向加速度比值分别为1∶0.85∶0.65或0.85∶1∶0.65，罕遇地震加速度峰值取0.44g，结构阻尼比取0.02。共考虑了6种工况(L0031XY，L0031YX，L0355XY，L0355YX，L845-8XY，L845-8YX)，其中工况人工波L845-8XY工况中XY代表X主向输入，其余工况以此类推。

图7 地震波反应谱曲线

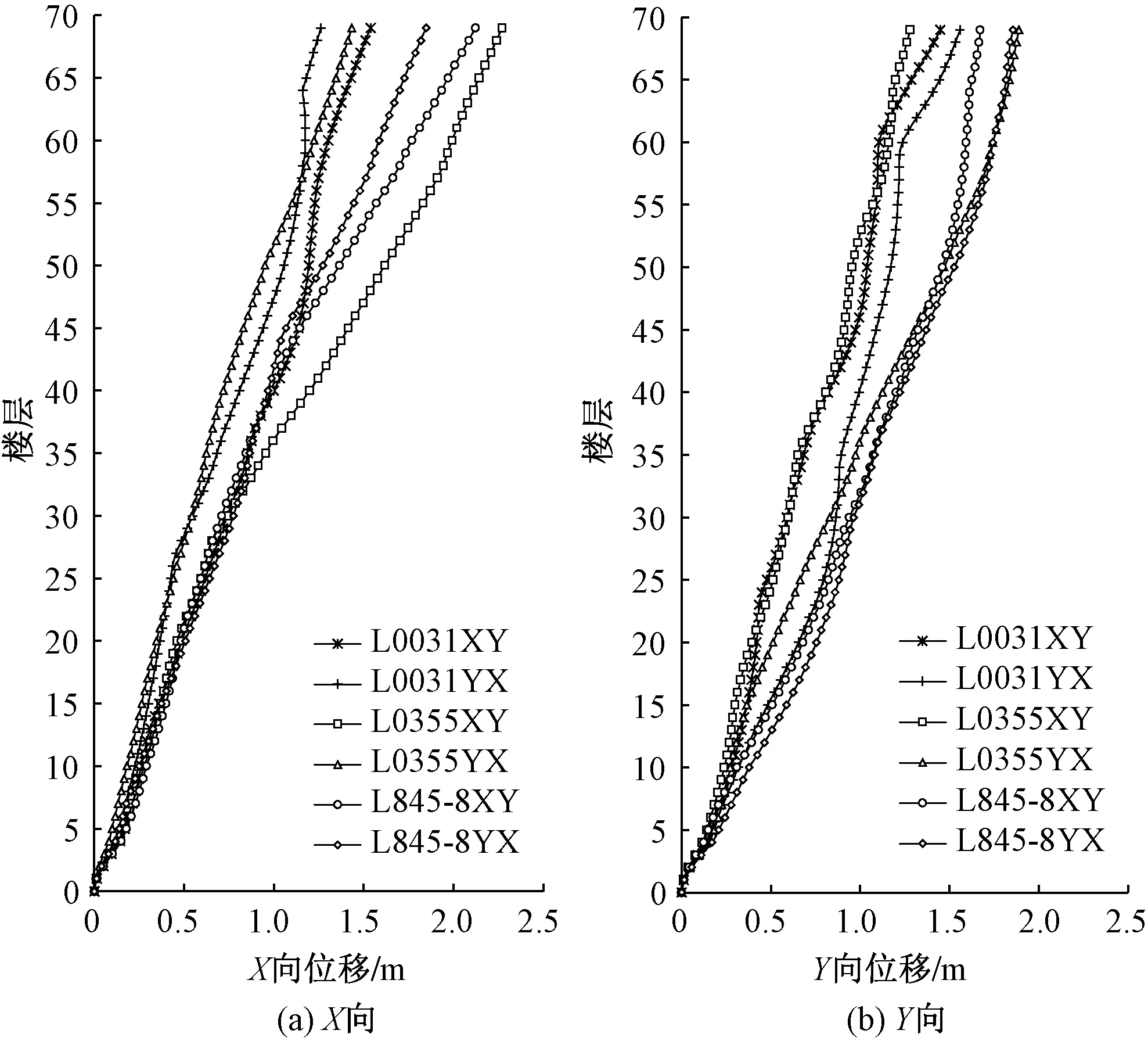
图8 结构X向和Y向各楼层最大位移

图9 结构X向和Y向各楼层最大层间位移角

4 罕遇地震下结构响应分析

在进行动力时程分析之前，进行了结构在重力荷载代表值作用下的施工过程模拟和重力加载分析，结构每5层为一个施工单元，包含伸臂后装施工步，一共16步，施工模拟和重力加载分析中后装伸臂轴力最大值为31kN。

4.1 结构位移分析

图8分别给出了各工况罕遇地震作用下结构各楼层X向和Y向最大位移，图中结构X向和Y向最大位移分别为2.38m和1.93m，分别出现在天然波L0355XY和L0355YX工况下。

结构X向和Y向各楼层最大层间位移角如图9所示，从图中可以看出，结构X向最大层间位移角出现在结构49层，出现在天然波L0355XY工况下，最大值为1/64。Y向最大层间位移角出现在结构62层，出现在天然波L0031YX工况下，最大值为1/72。X向和Y向层间位移角均小于钢结构大震弹塑性层间位移角限值1/50。

4.2 普通钢支撑地震响应分析

普通钢支撑是结构的第一道抗震防线中的构件，罕遇地震作用下普通钢支撑地震响应主要通过钢材的等效塑性应变PEEQ进行考察。PEEQ大于0，表明材料发生了屈服，该变量描述的是整个变形过程中塑性应变累积的绝对值之和，随着塑性发展逐渐增大。提取各工况地震输入完成后的结构状态即可得到钢管横截面四角积分点的塑性应变出现和发展情况。

各工况地震波输入结束后，钢支撑四角积分点包络等效塑性应变PEEQ。L845-8YX工况下钢支撑等效塑性应变如图10所示，从图中可见，约30%的普通钢支撑等效塑性应变PEEQ大于0，进入塑性的绝大部分普通钢支撑PEEQ小于0.01，加强层腰桁架中的普通钢支撑PEEQ小于0.003，塑性发展程度较轻。

普通钢支撑轴向塑性应变如图11所示，其中最大受压塑性应变为-0.003 2，最大受拉塑性应变为0.001 5，说明绝大部分进入塑性的普通钢支撑塑性发展程度较轻。加强层腰桁架中的普通钢支撑塑性应变小于0.003，塑性发展程度较轻。

4.3 BRB地震响应分析

BRB与普通钢支撑构成结构第一道抗震防线，罕遇地震作用下绝大部分BRB均屈服耗能。34层西南角伸臂BRB单元编号为81，87，85和75，人工波L845-8YX工况下34层西南角伸臂BRB单元滞回曲线如图12所示，图中可以看出伸臂处的BRB均屈服耗能，滞回曲线饱满，最大位移约32mm。

人工波L845-8YX工况下，结构下部2，3，6层的BRB滞回曲线如图13所示，从图中可以看出各BRB均充分屈服耗能，滞回曲线饱满，起到良好的消能效果，BRB最大变形小于40mm，未达到极限变形。

4.4 钢管混凝土柱地震响应分析

钢管混凝土柱为结构的第二道抗震防线中的构件，罕遇地震作用下钢管混凝土柱地震响应主要通过钢管柱中混凝土的应变及钢管塑性发展情况进行考察。钢管混凝土柱中混凝土应变如图14所示，从图中可以看出，局部柱边缘混凝土压应变绝对值小于0.002，混凝并未压溃。其他绝大部分混凝土压应变小于0.001 2，截面边缘混凝土进入塑性，但并未充分发展。

图10 L845-8YX工况下普通钢支撑等效塑性应变

图11 L845-8YX工况下普通钢支撑轴向塑性应变

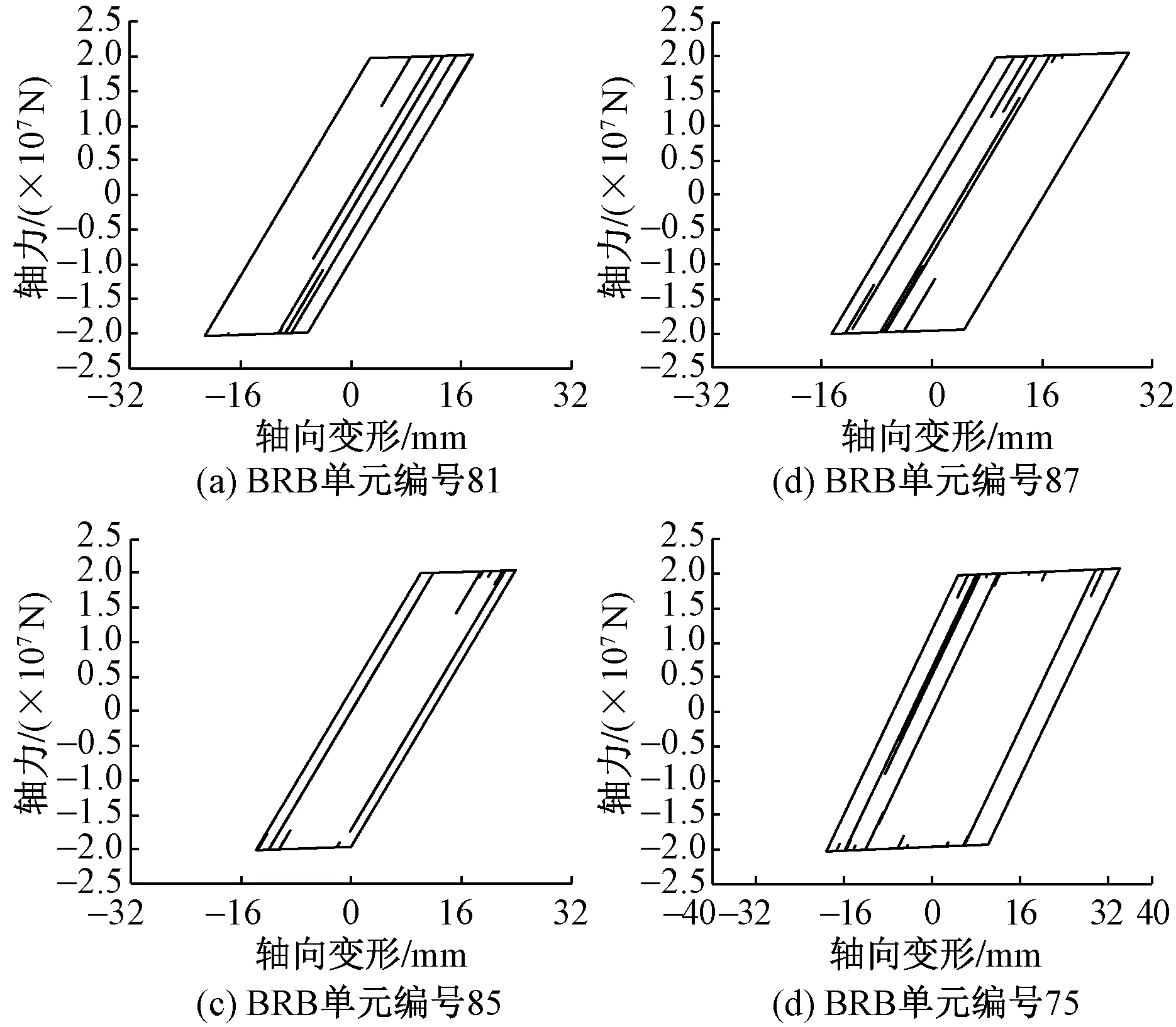
图12 人工波L845-8YX工况下34层西南角伸臂BRB单元滞回曲线

图13 人工波L845-8YX工况下结构2，3，6层BRB滞回曲线

地震波输入结束后，钢管四角积分点等效塑性应变PEEQ如图15所示，从图中可以看出，不同工况下约10%的钢管等效塑性应变PEEQ大于0，绝大部分进入塑性的钢支撑等效塑性应变PEEQ小于0.01，说明钢管峰值塑性应变绝对值之和小于0.01，绝大部分进入塑性的钢管柱塑性发展程度较轻。以上结果说明钢管混凝土柱还具有较高的剩余承载力，结构满足“大震不倒”的抗震设防目标。

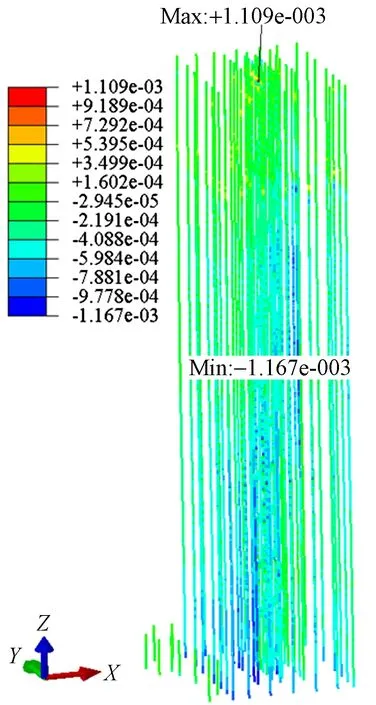
图14 L845-8XY工况下钢管柱中混凝土应变

图15 L845-8XY工况下钢管四角积分点等效塑性应变PEEQ

5 结论

某8度区超高层钢结构采用了863根普通钢支撑，并在结构底部加强区和伸臂桁架腹杆处设置了104根BRB，对结构抗震性能进行了分析，研究结果表明：

(1)伸臂桁架是本工程中的重要抗侧力构件，普通伸臂桁架由于斜腹杆受压屈曲导致耗能能力不足，将伸臂斜腹杆替换成BRB，可取得较好的消能减震效果。

(2)普通钢支撑为第一道抗震防线中的主要抗侧力构件之一，应考虑其拉压不对称滞回特性，采用施加初始几何缺陷的方法对普通钢支撑拉压不对称进行了模拟，结果表明初始几何缺陷对支撑初始轴力有较大影响，但对支撑整体的滞回曲线影响不大，普通钢支撑的长细比越大，初始几何缺陷导致受压承载力下降越显著。

(3)对整体结构进行了动力弹塑性时程分析，结果表明结构满足“大震不倒”的设防目标。