昆明呈贡重塑饱和红黏土的动变形特性试验

杨 正，屈俊童，季 东，字晓雷，刘 超

(1.云南大学 建筑与规划学院，云南 昆明 650504；2.金科地产集团股份有限公司，四川 成都 610066)

红黏土是一种工程地质性质特殊的土体，主要分布在热带和亚热带，有着高强度、低压缩性等工程性质，在我国的中部和西南部有着大范围的分布[1].红黏土由碳酸盐岩石形成，但其性质有别于碳酸盐岩石，具有液塑限高、孔隙比大和含水率高等物理性质，以及强度高、压缩性低的力学性质.同时，它还具有表层土较硬和下层土较软的分布不均匀特性、软胀缩性以及裂隙性等不良工程性质，给建筑工程、施工建设造成安全隐患.

土动力特性是研究红黏土力学性能的重要内容之一.其中土的动变形研究有着重要意义，是土层非线性地震响应数值计算和场地地震安全评估前提，是工程场地土工建筑物动力分析和设计的基本依据.有学者对红黏土及一系列工程软土的动力特性进行了研究，分析了围压[2-5]、动载频率[6-10]和固结比[11-12]对土的动力特性的影响，研究结果表明红黏土的力学特性具有区域差异性.受气候、形成因素等影响，不同地区的红黏土所表现出来的物理性质和力学性质有很大差异，所以目前有关红黏土特性的研究成果通用性不强.

昆明呈贡地区广泛分布着一层红褐色的石灰岩类红黏土，土层厚度变化极大，分布范围从地面到30多米深的地下都有.主要是经冲积形成的次生红黏土，具有其特有的动力学特性，且随着云南经济的发展，红黏土地区的工程项目日益增多，这就使得红黏土的动力学特性研究具有现实意义.为此，借助GDS动三轴仪对昆明呈贡地区的饱和红黏土进行研究，以期得到其动变形特性,以及不同试验条件对其动变形特性的影响，为云南地区的工程建设提供参考.

1 动三轴试验

1.1 试验材料和仪器

试验所用红黏土取自云南大学二期工程青教公寓场地，取土深度为4～5 m，呈贡地区抗震设防烈度为8度，所取土样为比较坚硬的褐黄色、褐红色石灰岩类红黏土，整体呈坚硬状，局部可塑，略微湿润.红黏土土样的物理性质指标如下：天然密度为1.93 g·cm-3，土粒比重为2.89，天然含水率为33.9%，孔隙比为1.015，饱和度为96.5%，塑限为34.2%，液限为59.7%，塑限指数为25.5，液限指数为-0.12.颗粒级配如下：中砂(0.500～0.250 mm)为4.8%，细砂(0.250～0.075 mm)为1.1%，粉砂(0.075～0.050 mm)为24.3%，粗粉粒(0.050～0.010 mm)为13.3%，细粉粒(0.010～0.005 mm)为8.0%，黏粒(<0.005 mm)为48.5%，胶粒(<0.002 mm)为43.7%.

试验所用仪器为英国生产的GDS伺服电机控制全自动单向激振动三轴仪.

1.2 试验结果

重塑土试样采用分层击实法进行制备.试样直径为50 mm，高度为100 mm.每组制备5个试样，2个备用试样.试样击实完毕，放入真空饱和缸，饱和36 h，之后安装试样.试样制备及安装流程为击实土样—真空饱和—放样、贴滤纸条—套橡皮膜—装拉伸帽—装压力室及注水.安装图见图1.

试样安装完成后进行反压饱和与孔隙压力系数(B)的检测.当B≥0.9时，认为试样达到饱和，然后在设定围压和固结比下充分排水固结，再选择不同动载频率，在不排水条件下逐级加载试验.输入的波形为正弦波，二维循环加载，每级循环次数选为10次.动荷载加载方案如表1所示.

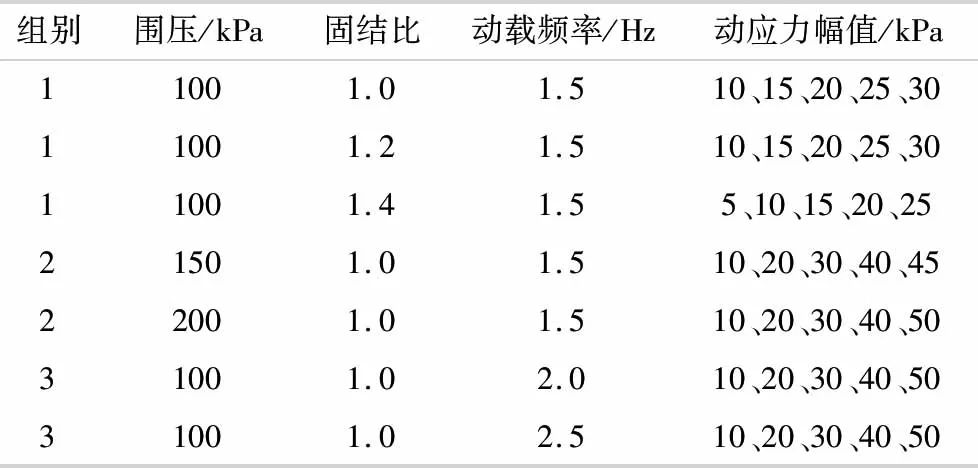
表1 动荷载加载方案

2 重塑红黏土动变形特性

土动变形特性的研究主要是获得动应力-动应变本构关系、动模量、最大动模量和阻尼比特性.动剪切模量、最大动剪切模量、阻尼比与动剪应变的关系曲线是评价地基动力稳定性和采用等效线性化方法分析土的地震反应非线性时的重要动力参数，对场地土的共振、滤波和放大效应等有重要影响.随着GB 17741—2005《工程场地地震安全性评价》的实施，对工程场地土动变形特性的研究也越发重要.

在动力测试阶段，按照每级5或10 kPa的动应力幅值等差分级施加动荷载，每级振动循环10次.为避免前几次振动的不稳定，选择第5次的滞回圈进行分析.连接各滞回圈的顶点连线即为骨干曲线，该曲线可以反映土动应力-动应变关系的非线性关系，并且通过骨干曲线求得动弹性模量与动剪切模量，即

(1)

(2)

式中：Ed为动弹性模量；σdmax、σdmin为最大、最小动应力；εdmax、εdmin为最大、最小动应变；Gd为动剪切模量；τd为动剪切应力；γd为动剪切应变；μ为泊松比，黏性土通常取0.5.

通过动三轴试验发现呈贡饱和红黏土的骨干曲线呈现双曲线.其动本构关系可用Hardin-Drnevich模型[12]来描述，即

(3)

(4)

式中：σd为动应力；a、b为试验参数.由式(4)可以看出，1/Ed与εd呈线性关系，在骨干曲线图上表现为直线.该斜直线的斜率为b，在纵轴上的截距为a.

可由双曲线Hardin-Drnevich模型的参数a计算最大动弹性模量，公式如下：

(5)

式中：Edmax为最大动弹性模量.Edmax在骨干曲线上表示为坐标原点处的切线斜率.

2.1 动应力动应变曲线影响因素分析

为了得到围压、动载频率和固结比对呈贡饱和红黏土的影响，将围压p、动载频率f、固结比kc设置为单一变量.动应力-动应变(σd-εd)骨干曲线的演化规律如图2所示.

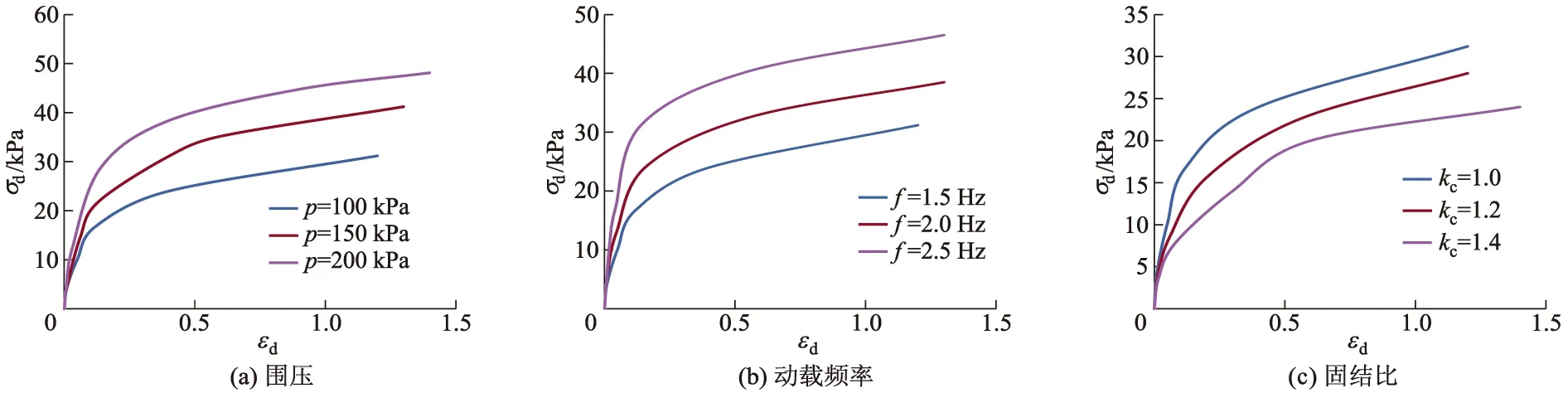
图2 不同围压、动载频率和固结比时的动应力-动应变骨干曲线

由图2a可知，固结比、动载频率一定时，相同动应变下，随着围压的增大，动应力值越大，动应力与围压呈正相关.可见围压增加，使土体内部颗粒间的咬合力和黏结力增加，导致土体抵抗变形的能力也随之增强.由图2b可知，固结比、围压一定时，相同动应变下，动应力随着动载频率的升高而升高.这主要是因为试验过程中存在循环效应作用，较大振动频率时，动荷载还没完全作用到土体上，荷载就发生了改变，总应力还未完全转化为有效应力.因此，动载频率越高，动应变越小.当动载频率越小时，土样变形发展反而越充分，土体破坏越严重.由图2c可知，围压、动载频率一定时，相同动应变下，动应力随着固结比增加而减小，可见该动应力对土样产生了一定的破坏作用，使得土样的抗剪强度下降.

2.2 动模量试验结果分析

选择每级循环荷载的第5个滞回圈进行分析，根据式(1)计算获得动弹性模量；根据式(3)、(4)，通过Hardin-Drnevich双曲线模型进行线性拟合，获得拟合参数a和b；由式(5)计算得到最大动弹性模量.将动应力、动应变换成动剪应力和动剪应变，重复上面运算过程，即可得到最大动剪切模量.

2.2.1围压对动弹性模量的影响

围压是影响土体特性的一个重要参数.在固结比为1.0，动载频率为1.5 Hz，围压为100、150和200 kPa时的动弹性模量-动应变曲线如图3所示.

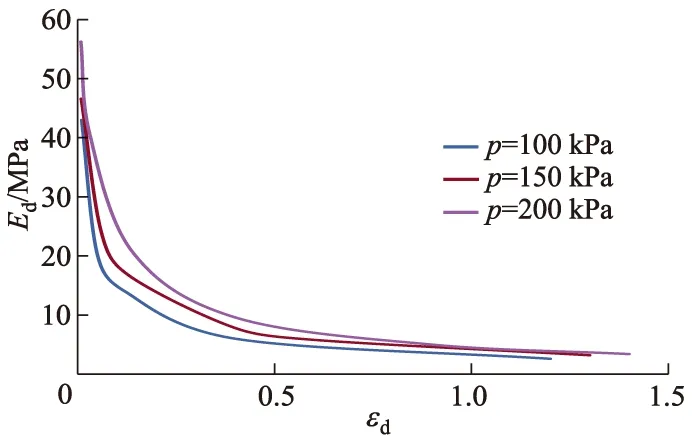
图3 不同围压下的动弹性模量-动应变曲线

由图3可知：当围压为200 kPa时，试样的动弹性模量达到最大值；动载频率一定，在同一动应变下，随着围压的增大，动弹性模量也升高.可见围压越大，土颗粒间越密实，其产生单位动应变所需的动应力也越大.不同围压下1/Ed-εd曲线如图4所示.

图4 不同围压下的1/Ed-εd曲线

根据式(4)，对图4中的曲线进行线性拟合，获得拟合参数a和b，并由式(5)计算得到最大动弹性模量和最大动剪切模量，结果如表2所示，表中R2为拟合指数.

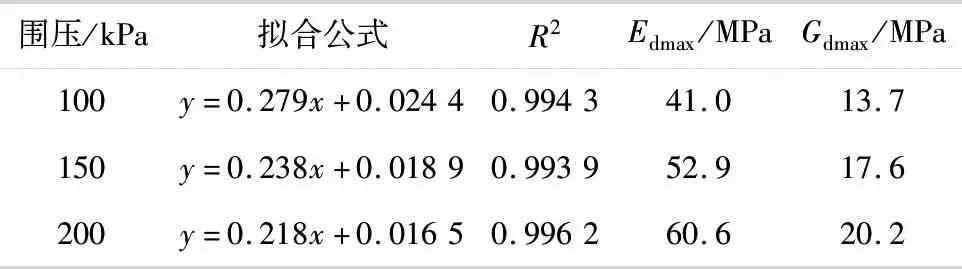
表2 不同围压下的双曲线拟合结果

由表2可知，各围压下的拟合判断参数R2均大于0.99，拟合效果良好，给出了拟合参数a、b.并得出了最大动弹性模量和最大动剪切模量，且二者均随着围压增大而增大.

2.2.2动载频率对动弹性模量的影响

在固结比为1.0，围压为100 kPa，动载频率为1.5、2.0和2.5 Hz时，动弹性模量-动应变曲线如图5所示.

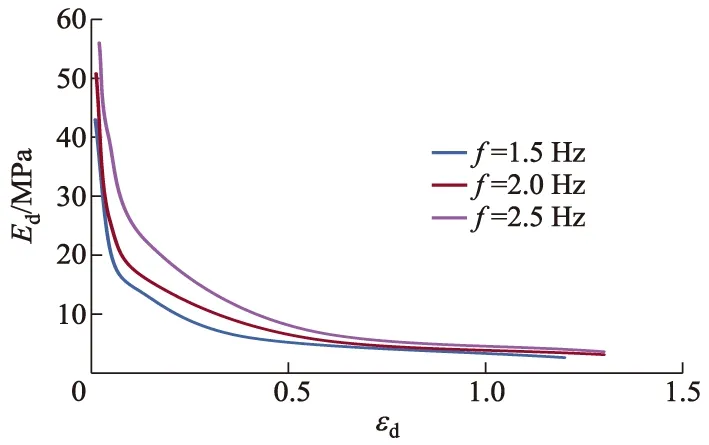
图5 不同动载频率下的动弹性模量-动应变曲线

由图5可知：不同动载频率下，动弹性模量-动应变曲线大体呈相同的变化趋势，动弹性模量均随着动应变的增加而减小；在相同的动应变下，动载频率越低，土样的动弹性模量越小；当动应变增加到一定值后，动载频率对动弹性模量的影响也逐渐地减小.不同动载频率下1/Ed-εd曲线如图6所示.

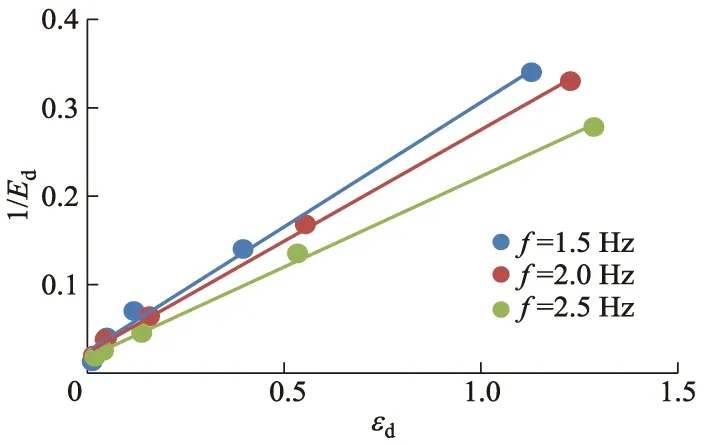
图6 不同动载频率下的1/Ed-εd曲线

根据Hardin-Drnevic双曲线模型对图6曲线进行拟合，获得拟合参数a和b，并求得最大动弹性模量Edmax和最大剪切模量Gdmax，结果如表3所示.

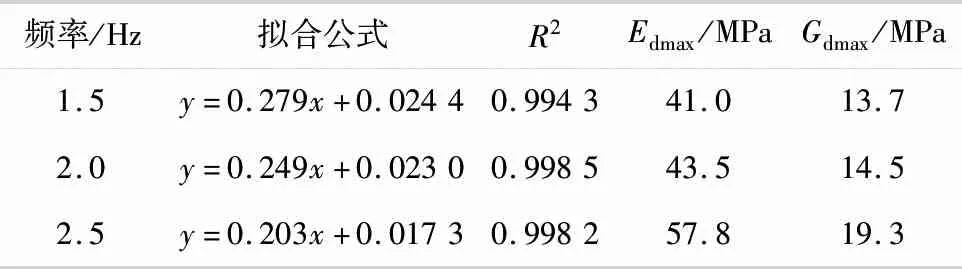
表3 不同动载频率下的双曲线拟合结果

由表3可知，各动载频率下的拟合判断参数R2均大于0.99，拟合效果良好，给出了拟合参数a和b，并得出了最大动弹性模量Edmax和最大动剪切模量Gdmax，且均随着动载频率增大而增大.

2.2.3固结比对动弹性模量的影响

动载频率为1.5 Hz，围压为100 kPa，固结比为1.0、1.2和1.4时，动弹性模量-动应变曲线见图7.由图7可知：不同固结比下，动弹性模量-动应变曲线变化趋势大体相同，动弹性模量均随着动应变的增加而减小；在相同的动应变下，固结比越高，土样的动弹性模量越小.这说明初始固结应力会对土样产生破坏，使土颗粒间变得松散，故而固结比越大，产生单位动应变所需的动应力越小.不同固结比下1/Ed-εd曲线如图8所示.

图7 不同固结比下的动弹性模量-动应变曲线

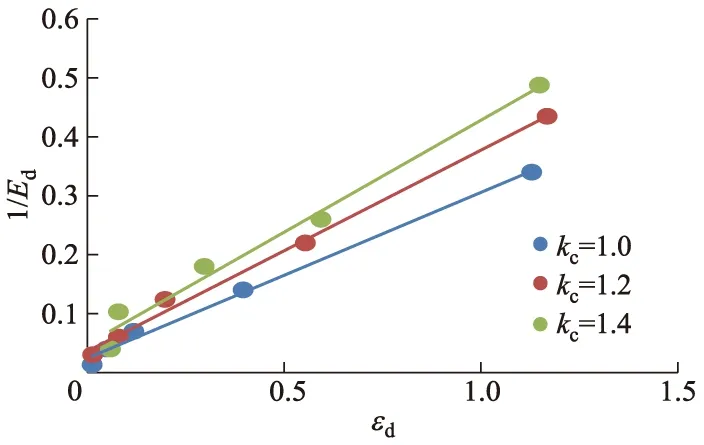
图8 不同固结比下的1/Ed-εd曲线

根据Hardin-Drnevic双曲线模型，对图8曲线进行拟合，获得拟合参数a和b，并求得Edmax和Gdmax，结果如表4所示.

由表4可知，各动载频率下拟合判断参数R2均大于0.98，拟合效果良好，给出了拟合参数a和b，并得出了最大动弹性模量Edmax和最大动剪切模量Gdmax，且均随着固结比增大而减小.

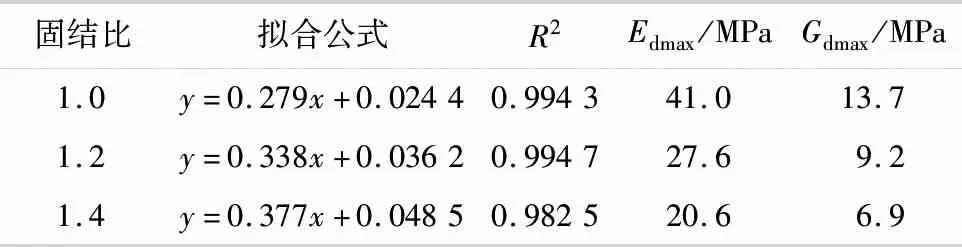
表4 不同固结比下的双曲线拟合结果

2.3 阻尼比试验结果分析

阻尼比λ反映了土体单元在动荷载作用下的能量损耗.图9为阻尼比计算示意图，图中A和C分别为滞回曲线右、左侧顶点，B为A在动应变轴上投影.

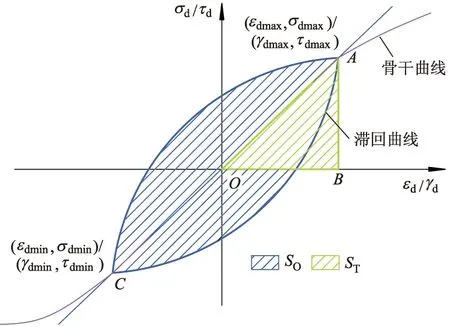
图9 阻尼比计算示意图

研究发现，可由经验公式求得等效阻尼比，即

(6)

式中：ST和SO分别为图9中三角形和滞回圈面积.

将围压、动载频率和固结比设置为单一变量，分析不同围压、动载频率和固结比对阻尼比的影响，其阻尼比-动应变曲线如图10所示.由图10可知：不同围压、动载频率和固结比下，阻尼比均随着动应变的增加而增加.

图10a中，同一动应变时，围压越大，阻尼比越小.可见由于围压增大，土颗粒间被压得越密实，从而使得土体中应力波的传播越流畅，所以重塑饱和红黏土的阻尼比越小.图10b中，同一动应变时，动载频率越低，土体的能量耗散越大，相应的阻尼比也越大.可见循环效应的存在使土体存在滞后性，低频荷载有利于土体动应变的发展，更易使土样发生破坏，使得应力波在土体内的传播受到阻碍.因此动载频率越低，重塑饱和红黏土的阻尼比越大.图10c中，当动应变相同时，固结比越大，土样的阻尼比也越大.说明固结比越大，固结应力对土样产生的破坏越严重，土样变得松散不利于应力波的传递，土的阻尼比也就越大.

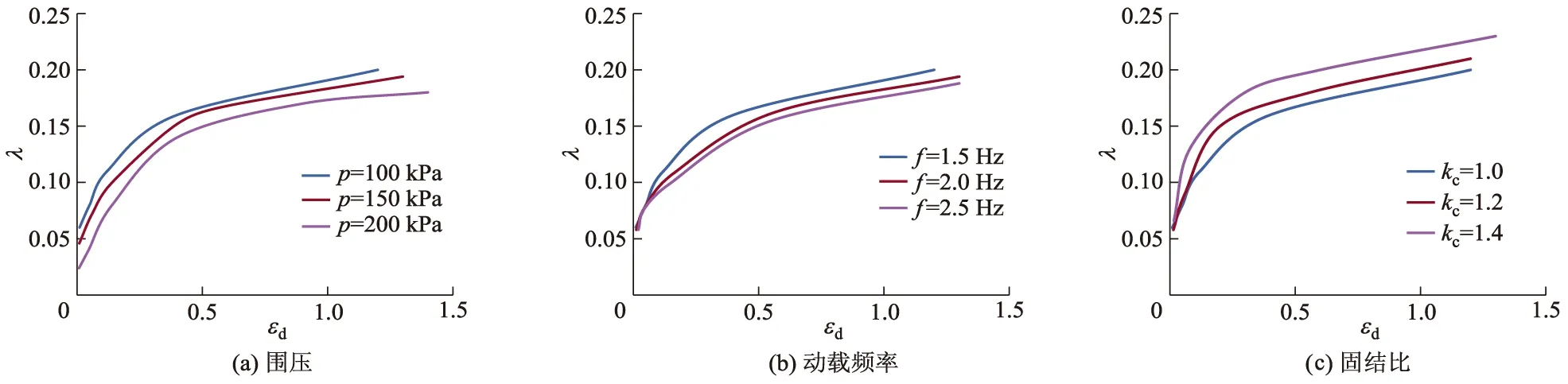
图10 不同围压、动载频率和固结比下的阻尼比-动应变曲线

3 结 论

1) 重塑饱和红黏土的骨干曲线呈现出明显的非线性增长关系，随着围压和动载频率的增大，骨干曲线达到相同动应变时所需的动应力越大；随着固结比的增大，骨干曲线达到相同动应变时所需的动应力越小.不同试验条件下的1/Ed-εd曲线都呈现出近似线性.用Hardin-Drnevich双曲线模型对重塑饱和红黏土的动本构关系进行拟合，拟合判断参数均大于0.96，拟合效果良好，可见利用该模型对重塑饱和红黏土的动本构关系进行拟合是可行的，并给出了重塑饱和红黏土的双曲线模型参数.

2) 不同试验条件下的动弹性模量-动应变曲线均呈现出非线性衰减趋势，动弹性模量具有明显的应变软化特征.动应变相同时，随着围压和动载频率的增大，重塑饱和红黏土的动弹性模量增大；随着固结比的增大，重塑饱和红黏土的动弹性模量减小.由Hardin-Drnevich双曲线模型的拟合参数计算得到重塑饱和红黏土的最大动弹性模量和最大动剪切模量.最大动弹性模量和最大动剪切模量随着围压和动载频率的增大而增大，随着固结比的增大而减小.

3) 不同试验条件下，随着围压和动载频率增大，阻尼比减小；随着固结比增大，阻尼比增大.