飞机变压整流器供电电路稳定性分析
杨占刚,蔡 进,黄 琨,徐海义
(中国民航大学 电子信息与自动化学院,天津 300300)
作为直流二次电源,变压整流器在供电系统中肩负着将交流电转换为直流电的重任,其工作性能的好坏将直接影响飞机供电系统的稳定性.文献[1]讨论了多台变压整流器并联供电方式给飞机供电系统带来的影响.文献[2]推导出供电系统数学模型,分析了整流器切换过程对供电系统稳定性的影响.文献[3]对多电飞机的混合交直流供电系统进行了小扰动稳定性分析,并通过试验验证了小扰动稳定性的分析结果.然而,目前关于变压整流器供电电路的分析只是讨论了变压整流器工作模式对系统稳定性的影响,却没有分析变压整流器参数对系统稳定性的影响,因此,有必要对变压整流器供电电路进行小扰动稳定性研究并分析参数对系统稳定性的影响.
在传统的小扰动稳定性分析中,模态分析方法(包括参与因子、阻尼比、振荡频率)被广泛用来分析系统的稳定性,这也是一直用来提取主要模态并且分析动态特性的有效方法.然而模态分析方法只能给出参数对系统稳定性的参与程度,却不能给出参数对稳定性的影响趋势.文献[4]首次提出了参数灵敏度这个概念,同时给出了一种用线性一阶微分方程来分析大型、多回路控制系统参数灵敏度的方法.这种参数灵敏度计算方法弥补了模态分析方法的缺点,因而被广泛应用到电力系统稳定器(power system stabilizer,PSS)的参数设计与优化中.文献[5]将改进的模态分析技术用于识别易受电力系统电压不稳定影响的弱节点.文献[6]提出了一种针对电力系统的新型灵敏度概念,即特征值运行方式灵敏度.与传统灵敏度计算方法相比,这种灵敏度计算方法更加直观,反映的是特征值对于系统运行方式的影响.以上两种特征值灵敏度分析方法属于静态分析方法,目前主要用于指导电力系统控制元件的选址和控制系统的参数设计.文献[7]利用特征值相对于符合特性系数的灵敏度来确定静止无功补偿器(static var compensator,SVC)的控制器放大倍数,以改善系统的动态响应;文献[8]对永磁同步发电机供电的直流配电电力系统(electrical power system,EPS)进行建模和小扰动稳定性分析,探究了特征值灵敏度以及系统运行条件对EPS稳定性的影响.文献[9-10]以灵敏度分析为基础,采用线性规定的方法整定PSS和可控串联补偿器(thyristor controlled series compensator,TCSC)控制系统参数.此外,灵敏度分析方法还被用于调整系统运行方式、辅助决策等.目前灵敏度分析方法应用主要针对系统级结构分析,并没有涉及具体供电电路的参数影响.文中利用灵敏度对变压整流器供电电路进行了参数灵敏度分析,具体分析了直流侧与交流侧供电电路线路参数对电路稳定性的影响.
文中首先采用dq变换法对飞机变压整流器供电电路进行等效变换,并由等效电路得到电路数学模型;然后对变压整流器供电电路进行潮流计算获取稳态工作点数据,并基于电路数学模型在稳态工作点对线路参数进行灵敏度计算,重点分析不同参数对变压整流器供电电路小扰动稳定性的影响趋势;最后利用Simulink进行仿真,验证灵敏度计算的正确性.
1 变压整流器供电电路数学模型
文中研究的变压整流器供电电路如图1所示,该供电电路由三相平衡电压源、传输线、六脉冲变压整流器、直流滤波器和一个等效的理想恒功率负载组成.Req、Leq、Ceq分别为传输线上的等效电阻、电感、电容.RCPL(constant power load,CPL)为理想的恒功率负载.rF、LF、CF分别为直流侧滤波器的电阻、电感、电容.Edc和Vout分别为整流器端和直流侧滤波器的输出电压,λ为源汇流条与交流汇流条之间的相移.

图1 变压整流器供电电路
对图1所示电路进行dq变换得到的等效电路见图2.

图2 变压整流器供电电路等效电路
针对图2中的等效电路,定义状态变量x=[IdsIqsVbus,dVbus,qIdcVout],输入变量u=[Iin,dPCPL],输出变量y=[Vout],其中:Ids和Iqs为经过电阻Req的电流在dq坐标系的分量,Vbus,d和Vbus,q为变压整流器输入端电压在dq坐标系的分量,Idc为变压整流器输出电流,Vout为恒功率负载两端电压,PCPL为恒功率负载端的负载功率.
等效电路的非线性状态方程组为
(1)
对式(1)进行线性化处理可得
(2)
由此,可求出系统的线性化状态方程参数,如下:

2 变压整流器供电电路潮流计算
在对该飞机供电系统求解稳定性问题前需求出稳态点的数值,该数值由图3进行潮流计算获得.图3为飞机供电系统电路从源汇流条到交流汇流条之间的潮流计算单线图.

图3 稳态点计算单线图
Ploss为整流器输出端等效电阻的损耗功率(忽略不计).由于变压整流器基波输入电流与输入电压相位一致,Qbus设为0.因此,可得交流汇流条处的有功功率Pbus和无功功率Qbus分别为
(3)
Qbus=0.
(4)
求出交流汇流条处的有功功率和无功功率的另外一种表达式,如下:
(5)
(6)
式中:Vs为三相交流电压有效值;Vbus为交流汇流条(变压整流器输入端)的稳态相电压.
对所研究的飞机供电系统参数进行初始化,如下:传输线电阻Req为0.1 Ω,电感Leq为24 μH,电容Ceq为1.5 mF;相电压Vs为230 V;频率ω为800π rad·s-1;直流侧电阻rF为0.01 Ω,电感LF为2 mH,电容CF为500 μF.
PCPL是随负载变化而变化的量,而其变化会影响电压值.因此可以根据负载值计算出交流侧的电压稳态值,然后根据变压整流器的交直流变换关系
(7)
结合式(3)-(6)可以得到直流侧在不同PCPL下的稳态电压值Vout和Idc,结果见表1.
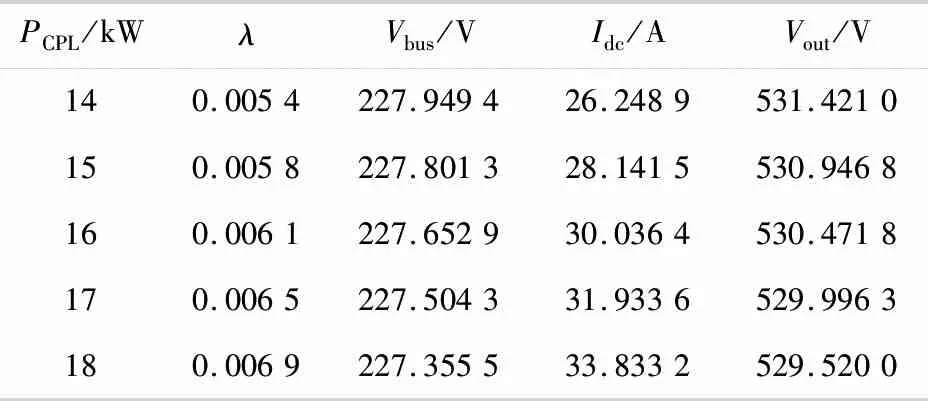
表1 不同功率情况下稳态点计算结果
3 参数灵敏度分析
3.1 特征值灵敏度计算
根据表1中不同功率潮流计算结果,计算状态矩阵A的特征值,利用特征值理论分析系统的小扰动稳定性.不同功率下的主导特征值计算结果见表2.

表2 不同功率下的主导特征值
由表2可见,随着PCPL的增大,系统特征值的实部也逐渐沿坐标轴虚轴右移,这意味着系统的稳定性变差,当PCPL=17 kW时,系统处于稳定与不稳定的临界点.因此选择PCPL=16 kW这个稳态工作点进行灵敏度计算,计算式为
(8)
式中:wiT、ui分别为特征值λi的左右特征向量;kj为要分析的参数.根据状态矩阵A和式(8),针对主导特征值λ计算的灵敏度结果见表3.

表3 参数灵敏度
计算得到的参数灵敏度为复数,其中实部、虚部分别反映了参数的变化对该振荡模式阻尼和振荡频率的影响.例如Leq的灵敏度数值为-2.396 8×1011+3.065 0×1010i,实部为负数,即当减小Leq时,主导特征值的实部逐渐沿坐标轴实轴右移,意味着系统的小扰动稳定性会变差.同理,可知当减小Req、CF时,主导特征值的实部会逐渐沿坐标轴右移,系统的小扰动稳定性会逐渐变差;当减小LF时,主导特征值的实部会逐渐沿坐标轴左移,系统的小扰动稳定性会逐渐变好.
3.2 仿真分析
为了验证参数灵敏度正确性,基于Matlab中的Simulink平台对图1中电路结构进行仿真分析.图4为根据A矩阵所计算的Req变化对系统特征根的影响趋势,图5为Req变化对输出电压影响的仿真图.
由图4可见,随着Req增大系统的稳定性越来越好.

图4 Req对特征根的影响
由图5可见,逐渐减小Req,输出电压的收敛性能越来越差,即系统稳定性能越来越差.图5验证了图4计算趋势与表3参数灵敏度分析结果的一致性.图6为根据A矩阵所计算的Leq变化对系统特征根的影响趋势,图7为Leq变化对输出电压影响的仿真图.

图5 Req变化对输出电压的影响

图6 Leq对特征根的影响

图7 Leq变化对输出电压的影响
由图6可见,随着Leq增大系统的稳定性越来越好.由图7可见,逐渐减小Leq,输出电压的收敛性能越来越差,即系统稳定性能越来越差.图7验证了图6计算趋势与表3参数灵敏度分析结果的一致性.图8为根据A矩阵所计算的rF变化对系统特征根的影响趋势,图9为rF变化对输出电压影响的仿真图.

图8 rF对特征根的影响

图9 rF变化对输出电压的影响
由图8可见,随着rF增大系统的稳定性越来越差.由图9可见,逐渐减小rF,输出电压的收敛性能越来越差,即系统稳定性能越来越差.图9验证了图8计算趋势与表3参数灵敏度分析结果的一致性.图10为根据A矩阵所计算的LF变化对系统特征根的影响趋势,图11为LF变化对输出电压影响的仿真图.

图10 LF对特征根的影响

图11 LF变化对输出电压的影响
由图10可见,随着LF增大系统的稳定性越来越差.由图11可见,逐渐减小LF,输出电压的收敛性能越来越好,即系统稳定性能越来越好.图11验证了图10计算趋势与表3参数灵敏度分析结果的一致性.
4 结 论
文中通过对飞机变压整流器供电电路进行dq变换得到数学模型,并在该数学模型的基础上研究了小扰动稳定性以及飞机供电系统的线路参数灵敏度,最后搭建仿真模型验证了理论计算的正确性.结果表明,增大交流侧电感、电流以及直流侧电感,或者减小直流侧电感和负载功率都有益于飞机供电系统的稳定性.

