基于PSO-SVM算法的软土复合固化剂最优配比
潘斌杰,朱剑锋,2,徐日庆
(1.宁波大学 土木与环境工程学院,浙江 宁波 315211;2.浙江科技学院 土木与建筑工程学院,浙江 杭州 310023;3.浙江大学 滨海和城市岩土工程研究中心,浙江 杭州310058;4.浙江加州国际纳米技术研究院 台州分院,浙江 台州 318000)
近年来,软土固化技术在东南沿海基础设施建设中得到了广泛应用.作为影响固化效果的关键因素,固化剂最优配比的研制引起了学者们的广泛关注.郭印等[1]和杨爱武等[2]以固化土的无侧限抗压强度(qu)为指标,通过正交试验分别确定了XGL2005型和CJDS07型复合固化剂的各组分之间的最优配比.庹秋水等[3]正交设计各种不同固化剂添加方案,结合直剪试验研究淤泥固化剂最优配比.然而,正交试验法无法建立复合固化剂各组分和固化土强度之间的函数关系,难以准确获得各添加剂的最优配比.于是,畅帅等[4]、李雪刚等[5]、朱剑锋等[6]通过开展旋转中心试验,构造固化土qu的响应面函数(RS),通过对RS求极值来确定软土复合固化剂最优配比,从而提出基于响应面法(response surface method,RSM)的软土复合固化剂配比优化方法.RSM虽然精度高,但是需要开展大量旋转中心试验来确定自变量的系数.当配比因子增加时,试验成本将呈几何式地增长,且响应面预测误差显著增加[7].
支持向量机(support vector machine,SVM)[8]因其在处理小样本、非线性、局部极小值等方面的独特优势,以其替代响应面法构造软土复合固化剂各组分与固化土强度之间的映射关系,将会显著降低试验成本.目前SVM已在边坡工程[9]、复合地基[10]等领域得到了广泛应用,并取得良好的预测效果.然而,SVM模型仅提供了固化剂各掺量与固化土强度之间精确的映射关系,而无法给出明确的关系表达式,因此,需要结合智能优化算法来确定软土复合固化剂的最优配比.
目前,在土木工程中得到的应用智能优化算法主要有遗传算法[11]、禁忌-遗传算法[12]、粒子群算法[7]等.其中,作为一种模拟生物活动性、全局性优化算法——粒子群算法(particle swarm optimization,PSO),以其良好的鲁棒性、进化性及随机性在岩土工程中得到了广泛应用.YI P.等[7]建立了边坡可靠性分析累积PSO-Kriging模型.王峰等[13]利用改进的PSO,反演分析了某拱坝高温季节热学参数.
为此,将SVM和PSO进行有机耦合,根据试验结果建立软土复合固化剂各组分与固化土qu之间的映射关系,建立基于SVM的固化土qu的预测模型;然后,以固化土的最大无侧限抗压强度(qumax)为目标函数值,采用PSO算法搜索软土复合固化剂的最优配比,提出软土复合固化剂最优配比的PSO-SVM耦合算法,最后结合试验结果对该算法的可行性进行验证.
1 PSO-SVM优化算法
1.1 基于SVM的固化土qu预测模型
基于统计学习理论的SVM是根据结构风险最小原理演绎建立,结合有限的样本信息,在模型复杂性和学习能力之间寻求最佳折中,以期获得最好的泛化能力[8].如图1所示,基于SVM固化土配方的qu预测模型建立是以非线性回归预测原理为基础,以影响qu的固化剂各成分掺入比为输入变量,以某一龄期下对应的qu为输出变量,利用SVM的核函数寻求变量间最佳映射关系的过程.

图1 基于SVM的固化土配方与强度关系模型示意图
利用固化土强度试验数据回归出φ(x)函数,SVM采用以下函数进行拟合:
qu(x)=w′φ(x)+b,
(1)
式中:x是固化剂配方的配比;qu(x)为回归函数返回的预测值,这里指固化土强度预测值;φ(x)为非线性映射函数,这里指固化剂各成分掺入比与无侧限抗压强度间的映射关系;w′为赋值权重;b为偏差.定义线型不敏感损失函数[8]为
L(qu(x),y,ε)=

(2)
式中:y为对应的真实值,即固化土强度实测值;ε为固化土强度回归函数的误差精度.
若y与qu(x)之间的误差绝对值小于等于ε,则表示损失为0.为求得式(1)中的w′、b,同时考虑到允许固化土强度预测中的拟合误差存在的情况,采用最小泛函数对其进行分析.将式(2)引入松弛变量ξi和ξi*,即变成数学规划寻优问题,式(2)可改写为
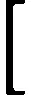
(3)
s.t.yi-w′φ(x)-b≤ε+ξi,-yi+w′φ(x)+
b≤ε+ξi*,ξi,ξi*≥0,i=1,2,…,Nt,
式中:C为惩罚因子,表示固化土强度回归函数复杂性与平均损失的权重系数;ε越小,表示回归函数的误差越小,本研究取ε=10-4;Nt为试样个数,个;yi为第i个样本的真实值,kPa;通过Largrange函数将式(3)转换为对偶问题,即
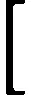
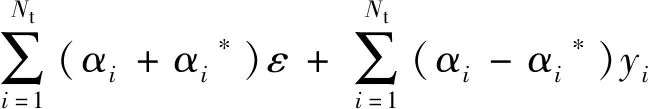
(4)
式中:k是对偶问题i的另一个形式,k=1,2,…,Nt;K(xi,xk)=φ(xi)φ(xk)为核函数.鉴于影响固化土的qu因素众多(掺入比、龄期、养护条件等),且它们之间关系通常呈非线性变化规律[4-6],因此采用工程中常用的非线性核函数——RBF核函数[8]来反映这一特性.即
K(x,x′)=exp(-γ‖x-x′‖2),
(5)
其中γ为RBF核函数的方差.由于RBF核函数参数γ和惩罚因子C的不同组合决定固化土qu预测模型的优劣,本研究利用网格搜索法和交叉验证方法[14]寻找最佳参数惩罚因子C和核函数的方差γ.
假设式(4)的最优解为α=[α1,α2,…,αNt],α*=[α1*,α2*,…,αNt*],则有:
(6)
(7)
固化土强度测试样本回归函数qu(x)可表示为
(8)
模型训练完成后,便可以建立某一个龄期下软土复合固化剂各成分掺入比与qu之间的映射关系,从而实现任意掺入比下固化土qu的仿真预测.现引入相关系数R2和均方误差σ2作为性能的评价,相关公式为
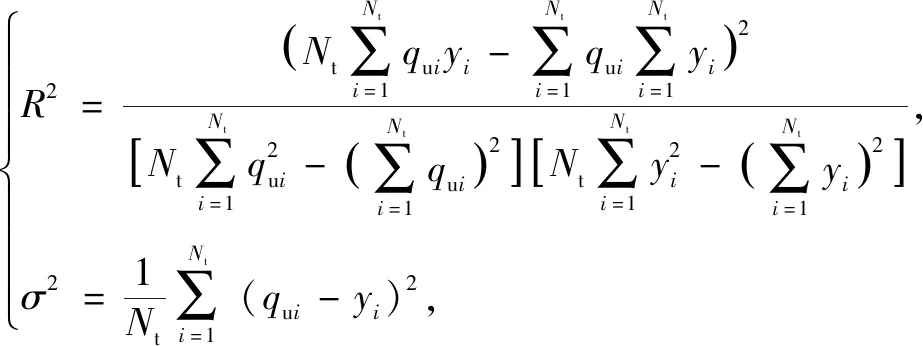
(9)
式中:qui为第i个样本的预测值,kPa.
1.2 粒子群算法基本原理
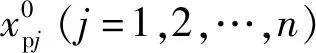
(10)
式中:xjmax和xjmin分别为粒子中第j个变量的最大值和最小值,即软土复合固化剂配方中第j成分的掺入比取值的上、下限;r为[0,1]的随机数.后续每次迭代过程中粒子更新满足下式[15]:
(11)
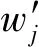
惯性权重可采用线性递减[15]方式计算:
(12)

1.3 基于PSO-SVM的固化剂最优配比确定
图2为软土复合固化剂最优配比PSO-SVM算法流程图.图2中,首先根据某一龄期下固化土的qu试验结果构建基于SVM的固化土qu预测模型,以此模型评价PSO算法中每一个粒子(复合固化剂配比)对应的目标函数值(qu);然后通过PSO算法进行软土复合固化剂成分配比的优化;最后输出最优配比,从而实现软土复合固化剂配比的PSO-SVM优化算法.

图2 软土复合固化剂最优配比PSO-SVM算法流程
2 模型验证
基于SVM的固化土qu预测模型是PSO-SVM优化算法的基础,其准确性直接关系到PSO中各粒子的适应度的评价精度,因此选取文献[6]的16组硫氧镁复合水泥固化剂(TZ18)的各成分(即水玻璃、熟料和硅灰)配比及相应的qu(7 d) 作为样本来构建SVM模型,以剩余4组试验结果作为目标验证集,分别采用SVM模型和响应面法[6]对其进行预测,预测结果如图3所示.通过网格搜索法和交叉验证法[14]获得参数C=1.148 7和γ=0.5.由图3可知,验证集中SVM模型的预测结果与文献[6]RSM预测结果均和实测值比较接近.本研究中预测结果相关系数R2=0.992,高于文献[6]的R2=0.852,而本研究模型均方误差σ2为0.939%,小于文献[6]的均方误差2.213%.因此,SVM模型预测精度优于RSM模型.
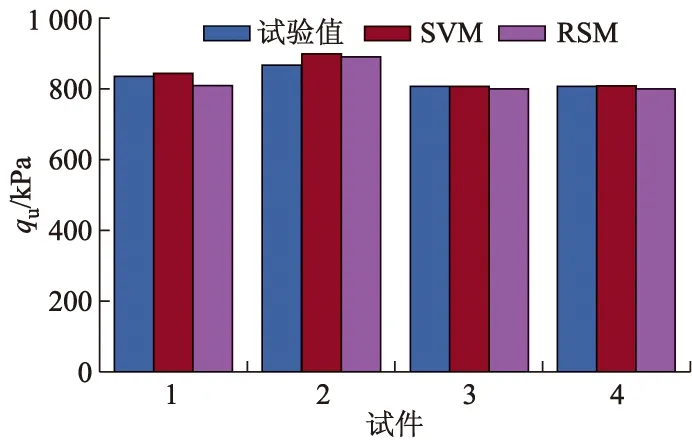
图3 固化土的qu (7 d)预测值与实测值对比


表1 PSO模型参数

表2 TZ18固化剂最优配比及PSO-SVM预测结果
由表2可知,PSO-SVM算法预测的TZ18复合固化剂的最优配比为w(水玻璃)=5.85%,w(熟料)=5.51%,w(硅灰)=6.45%,相应固化土的qu(7 d) 为1 090.55 kPa.为了预测有效性,根据该配比开展了TZ18固化土的7 d无侧限抗压强度试验.图4为试验中应力-应变(σ-ε1)曲线.取试样1和2测得qu的平均值作为本配方下试验的实测值(固化7 d的qu=1 156.06 kPa).通过计算,本研究中相对误差(相对误差=(qu实测值-qu预测值)/qu实测值×100%)为5.66%.而文献[6]RSM预测的相应固化土的qu(7 d)为1 042.45 kPa,本研究中依据RSM预测配方所做试样的qu(7 d) 实测值为949.04 kPa,二者相对误差为9.84%.因此,PSO-SVM算法高于文献[6]的预测精度.
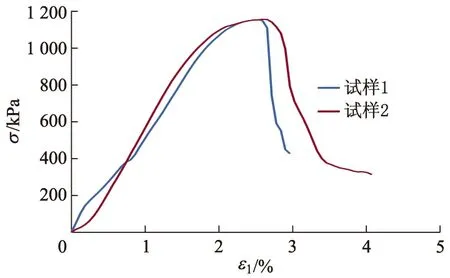
图4 TZ18固化剂最优配比预测值下σ-ε1曲线
为进一步验证PSO-SVM模型普适性,选取文献[4]的20组水泥复合固化剂(生石膏+生石灰+碳酸钠)的最优配比为目标值,分别采用PSO-SVM耦合算法和响应面法进行预测,并与试验结果进行对比.SVM模型参数C和γ经网格搜索和交叉验证均为1.515 7,参数ε=10-4.表3为软土复合固化剂最优配比及模型预测结果,其中软土复合固化剂最优配比指的是生石膏、生石灰和碳酸钠的质量分数比值的最佳值.

表3 软土复合固化剂最优配比及预测模型结果
软土复合固化剂最优配比优化范围见表1中的算例2.由表3可知,PSO-SVM算法预测的文献[4]软土复合固化剂最优配比为w(生石膏)=4.58%,w(生石灰)=4.10%,w(碳酸钠)=1.09%,相应的qu(7 d)为628.06 kPa.
图5为最优配比预测值下的软土复合固化剂
qu(7 d)试验σ-ε1曲线.由图5可知,该配比下固化土qu(7 d)实测值为634.15 kPa(取试样3和4,测得qu的峰值平均值),预测值和实测值间相对误差仅为0.96%.文献[4]RSM预测的最优配比为w(生石膏)=4.80%,w(生石灰)=3.56%,w(碳酸钠)=1.33%,相应的qu(7 d)为634.05 kPa,而文献[4]中RSM抗压强度实测值为623.00 kPa,二者相对误差为1.77%.可见,PSO-SVM算法在最优配比和预测精度方面均优于文献[4]的RSM.
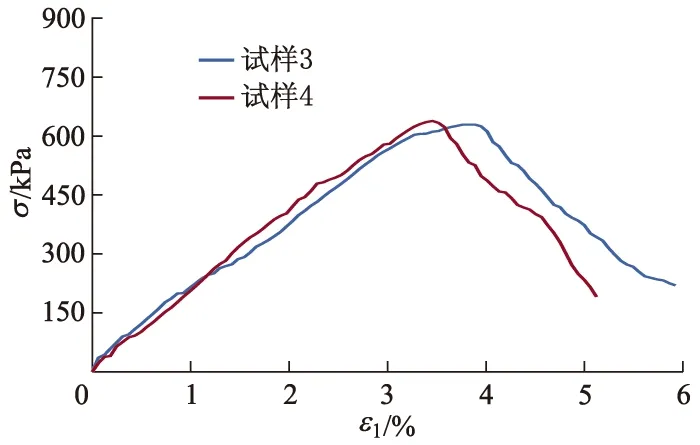
图5 软土固化剂最优配比预测值下的σ-ε1曲线
3 讨 论
在粒子群算法中Nmax和Np对搜索效率影响显著.现分别以文献[6]TZ18固化土和文献[4]复合固化土的试验数据为研究对象,采用PSO-SVM算法,搜索不同Nmax和Np时文献[6]TZ18复合固化剂(其他参数见表1中算例1)和文献[4]软土复合固化剂(其他参数见表1中算例2)的最优配比及相应的qu与所需时间t(算法运算的电脑系统配置为Inter(R) Pentium(R) CPU G630@2.70 GHz、4.00 G内存).图6和7分别为不同最大迭代次数(Nmax)下预测2种固化剂的最优配比、无侧限抗压强度(qu)及耗时(t)曲线.
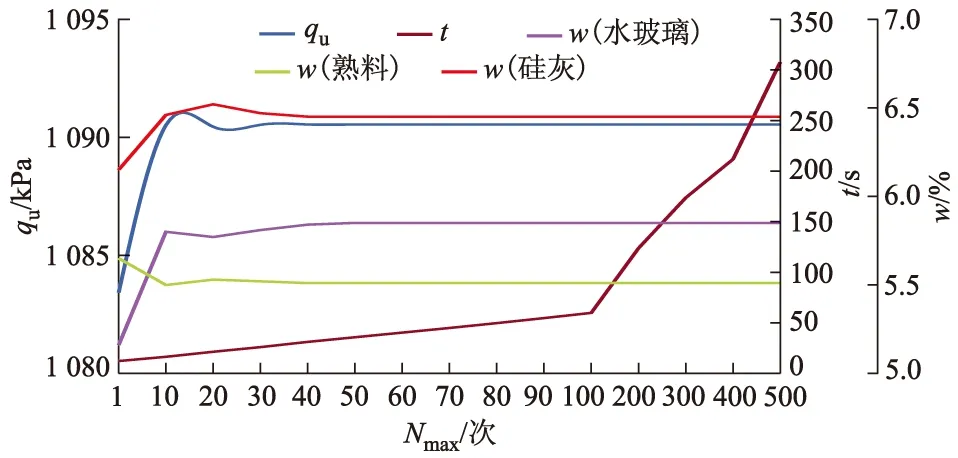
图6 不同Nmax下预测TZ18固化剂最优配比、qu及t
由图6可知:随着Nmax的增加,耗时也逐渐递增;虽然在Nmax=40 次时,固化土的qu(7 d)已经达到最优强度,但是TZ18复合固化剂各成分的配比还没有稳定;在Nmax=50 次时,搜索获得了TZ18复合固化剂的最优配比和最优强度保持稳定,此时耗时约35.71 s.图7同样表明:虽然在Nmax=40 次时,固化土的qu(7 d)已经达到最优强度,但是各成分的配比尚未稳定;在Nmax=60 次时,搜索获得最优配比和最优强度保持稳定,此时耗时约41.07 s.因此,复合固化剂最优配比的确定是一个多峰极值问题.采用PSO-SVM算法搜索复合固化剂的最优配比可以避免陷入局部最优解.当Nmax继续增加时,虽然能获得最优解,但是计算成本(耗时)过大.综上可知,Nmax≥60 次时,PSO-SVM搜索的最优配比基本收敛,而且运算时间在45 s以内.因此,建议采用PSO-SVM算法搜索固化剂最优配比时,取Nmax≥60 次.
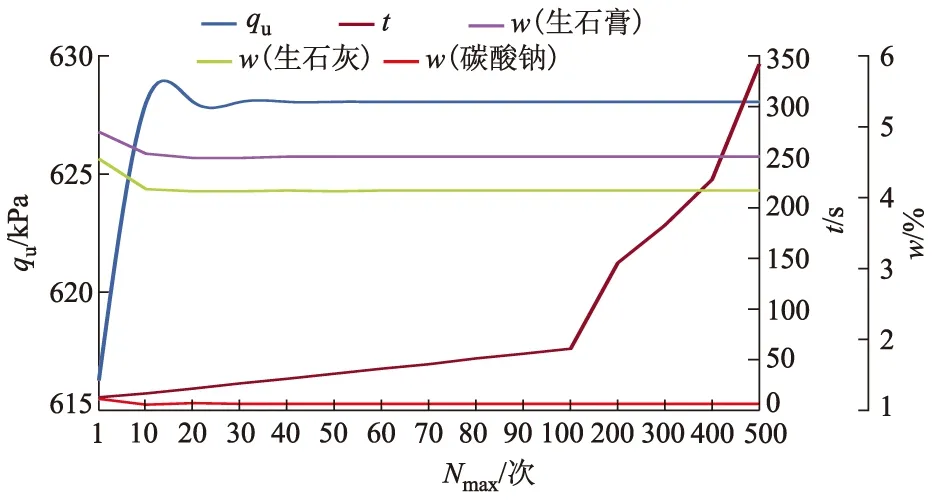
图7 不同Nmax下预测软土固化剂最优配比、qu及t
图8和9分别为不同粒子数(Np)下预测2种固化剂的最优配比、无侧限抗压强度(qu)及耗时(t)曲线.
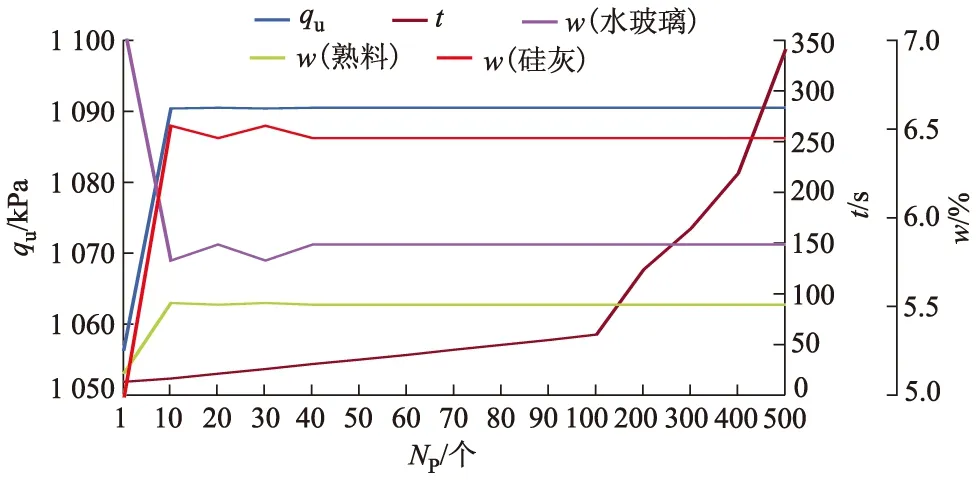
图8 不同Np下预测TZ18固化剂最优配比、qu及t
由图8可知,与Nmax规律类似,计算成本(耗时)随着粒子数(Np)的增加而增大.在粒子群规模较小(Np=20 个)时,采用PSO-SVM算法搜索获得的最优配比容易陷入局部最优,尽管预测的固化土qu(7 d)已接近最优,但各成分的配比尚未稳定.只有在Np≥40 个时,才获得最优配比和最优强度基本稳定,耗时约30.80 s.图9表明,当Np≥10 个时,预测的固化土qu(7 d)和各成分配比已基本稳定,耗时约16.28 s.综上可知,在采用PSO-SVM算法搜索软土复合固化剂最优配比时,建议Np≥40 个.
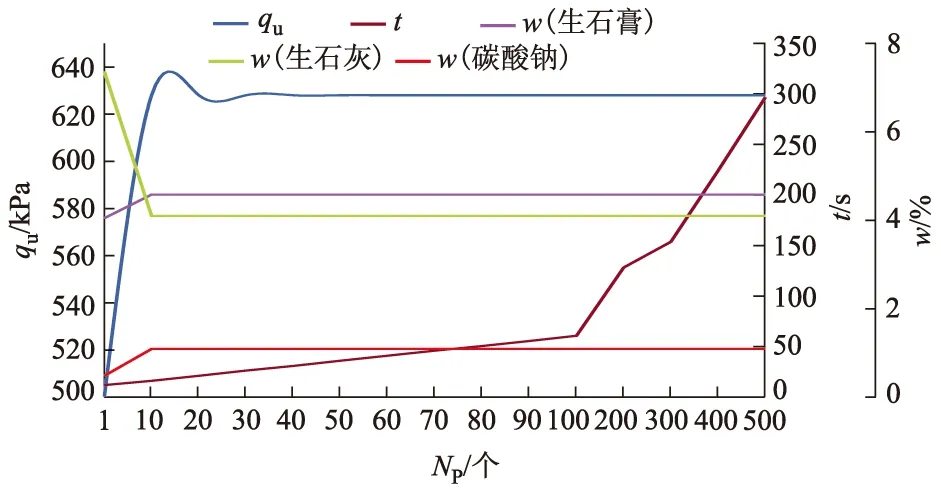
图9 不同Np下预测软土固化剂最优配比、qu及t
4 结 论
1) 根据固化土无侧限抗压强度(qu)试验结果,构建了基于SVM的固化土qu预测模型,算例分析表明SVM模型的预测精度优于RSM模型.
2) 以某一龄期下固化土无侧限抗压强度最大值(qumax)为目标函数,采用SVM模型预测复合固化剂任意配比下的qu,利用PSO算法搜索复合固化剂的最优配比,提出了软土复合固化剂最优配比的PSO-SVM算法.通过预测和试验结果对比分析可知,该算法获得的最优配比的预测精度高于RSM法.
3) 软土复合固化剂最优配比的确定是一个多峰极值问题.PSO-SVM算法参数Nmax和Np对搜索效率和预测结果影响显著,为避免陷入局部最优解,采用PSO-SVM搜索软土复合固化剂最优配比时,取Nmax≥60 次,Np≥40 个.

