波形钢腹板箱梁的腹板受力性能及桥面板横向内力分析
赵 品,荣学亮,叶见曙,陈 伟,王国安
(1.石家庄铁道大学 土木工程学院,河北 石家庄 050043;2.东南大学 交通学院,江苏 南京 210096)
波形钢腹板箱梁为钢混组合结构,波形钢腹板代替了传统的混凝土腹板,腹板材质、形状改变的同时,其厚度也降低很多,钢腹板对桥面板的支撑弱于混凝土腹板对桥面板的支撑.因此,波形钢腹板组合箱梁桥面板的约束及箱梁闭合框架的畸变、扭转与混凝土箱梁相比均有所不同,波形钢腹板箱梁桥面板和混凝土箱梁桥面板的横向内力相比会有所变化[1-9].
文献[7]基于框架分析法的基本原理,结合波形钢腹板箱梁的结构特点和力学特性,建立了适用于其桥面板横向内力的计算模型,该计算模型能够反映横向框架作用和箱梁畸变效应对桥面板横向内力的影响.文献[8]通过试验研究了波形钢腹板箱梁桥面板的有效分布宽度变化规律,并结合现行JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》和有限元结果,在对3种有效分布宽度计算值进行比较的基础上,对现行JTG 3362—2018进行修正,得到不同工况下的有效分布宽度修正系数.文献[10]通过室内试验提出了弹性屈曲强度简化计算公式,研究了波形钢腹板的抗剪受力性能.文献[11]在引入腹板剪切变形转角函数的基础上,建立了一个能够考虑波形钢腹板剪切变形的波形钢腹板梁理论模型,来研究波形钢腹板剪切变形对波形钢腹板梁受力行为的影响.
综上可知,已有文献对于波形钢腹板箱梁桥面板的横向内力计算和波形钢腹板的抗剪性能均有研究,但是对于荷载作用下波形钢腹板箱梁的混凝土桥面板和波形钢腹板各自的受力特点及其相互影响尚未有分析,为此,通过试验对上述两种板件的受力进行分析,探讨该钢混组合结构中两种板件的相互影响.
1 试验模型
JTG 3362—2018分析了主梁与梁肋刚度的对比对桥面板横向受力的影响,即以固支或简支两种方式假设主梁梁肋对行车道板的支撑,实际上行车道板和主梁梁肋的支撑条件,既不是固端也不是铰支,而应该考虑是弹性固结,如图1所示为竖向荷载p作用下的3种支撑形式.而箱梁桥面板的横向受力与腹板的约束程度有关,桥面板的横向内力随着对其约束的不同而发生变化.

图1 主梁扭转对行车道板受力的影响
本研究中将以波形钢腹板单箱双室试验梁为研究对象,通过钢腹板的位移及应变实测数据,分析钢腹板对混凝土桥面板的支撑特点.
通过室内模型试验,对波形钢腹板箱梁在横向不同位置荷载作用下的腹板变形进行监测,将通过腹板的变形及桥面板的受力对波形钢腹板箱梁的腹板支撑状况进行深入分析.为确定上述箱梁桥面板的横向受力,对1片波形钢腹板试验梁进行了试验研究.
1.1 模型概况
波形钢腹板单箱双室试验梁的截面尺寸和配筋如图2所示.箱梁总长为3 500 mm,计算跨径为3 300 mm.桥面板横断面宽度为2 000 mm,厚度为80 mm.箱梁混凝土的实测立方体抗压强度为28.3 MPa,弹性模量Ec=2.8×104MPa.波形钢腹板采用Q235C钢板,板高度为300 mm,板厚度为2 mm,折叠角度为37.0°,波的高度为24 mm,波长度为144 mm,试验屈服强度为194.5 MPa,抗拉强度为295.1 MPa.

图2 试验加载装置(单位:mm)
图3为位移计和应变片布置示意图[9].试验梁跨中截面的实测位移结果如图4所示.
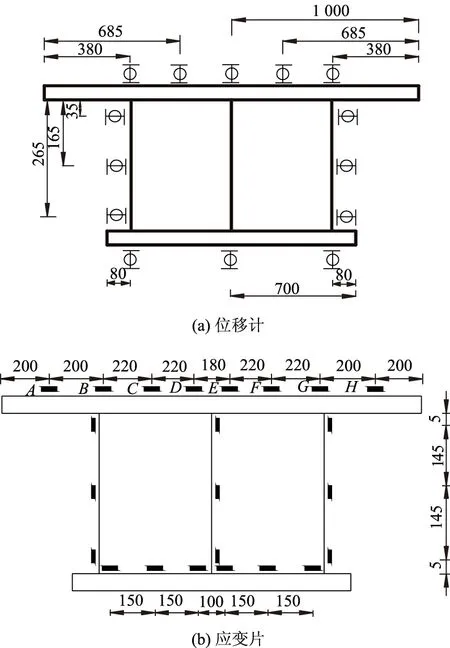
图3 位移计和应变片横向布置示意图 (单位:mm)

图4 试验梁跨中截面的实测位移 (单位:mm)
为了解荷载作用下箱梁框架的整体变形特征,同时测试波形钢腹板的侧向位移.在试验条件允许范围内在跨中截面和支点截面的混凝土顶板、混凝土底板、波形钢腹板上布设千分表,用以测量腹板的侧向位移[4],见图3a.
为测得荷载作用下箱梁顶板的横向内力分布曲线,在横向加载位置、腹板处的顶板位置等横向位置均布置了应变片,同样在底板的相应位置也布置了应变片,见图3b.
图4中,由于试验条件的限制,仅测得两侧边腹板的侧向变形.单个数字为箱梁板件竖向或横向的位移,对于带括号的2个数字,前者为横向位移,后者为竖向位移.顶板、腹板及底板的变形均随着横向加载位置的不同而变化,箱梁框架整体变形亦随之改变.
1.2 波形钢腹板在横向荷载下的纵、竖向变形
对于单箱双室箱梁而言,由中腹板、两侧边腹板及底板共同形成框架结构来承受作用在箱梁顶板上的荷载.试验对边腹板、中腹板的纵向及竖向应变进行了测试,以期对箱梁各腹板的应变变化规律进行分析,找出其对顶板横向受力的影响.以两种工况加载下的试验梁各个腹板的纵、竖向应变为观测对象测试试验.
图5为试验梁腹板在工况Ⅰ各级加载值下沿腹板高度方向的纵向和竖向应变曲线.由图5可知:远离荷载的边腹板在竖直方向的纵向应变均为拉应变;近荷载处的边腹板纵向应变亦为拉应变;中腹板的纵向应变则从上向下由压应变转化为拉应变;近荷载的边腹板竖向应变均为压应变;而中腹板和远离荷载的边腹板在竖直方向的竖向应变由拉应变转化成压应变.
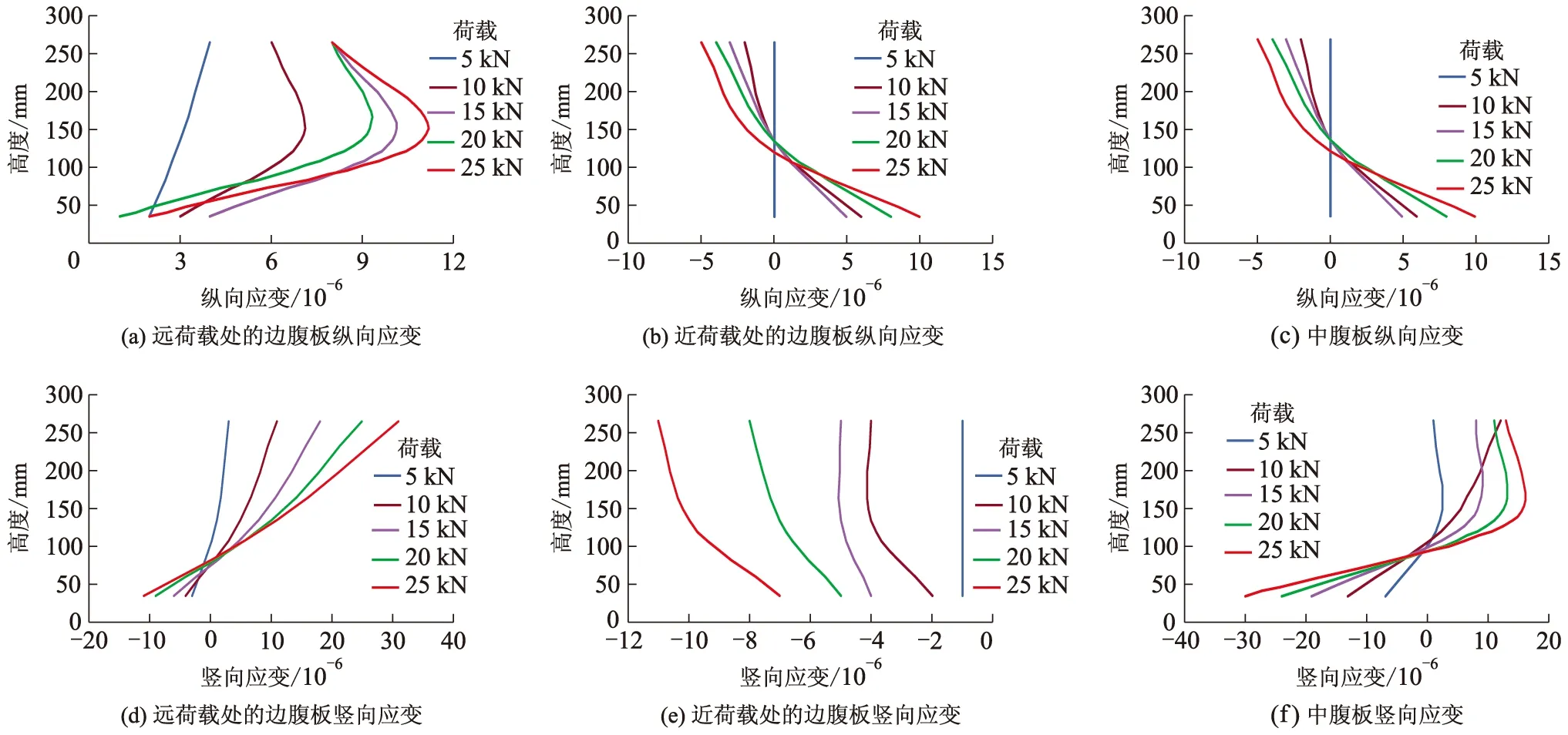
图5 试验梁腹板偏载下的纵、竖向应变曲线
图6为试验梁腹板在工况Ⅱ各级加载值下纵向应变和竖向应变曲线.由图6可知:远离荷载的边腹板在竖直方向的纵向应变均为压应变;近荷载位置处的边腹板纵向应变则有部分拉应变逐渐转化成压应变,但是绝大多数为拉应变;远离荷载的边腹板沿竖直方向上的竖向应变由上向下从拉应变逐渐转化为压应变;近荷载位置处的边腹板竖向应变则为压应变.
数据均使用软件SPSS22.0进行统一处理与分析,组间数据有差异性即P<0.05;组间数据无差异性即P>0.05。
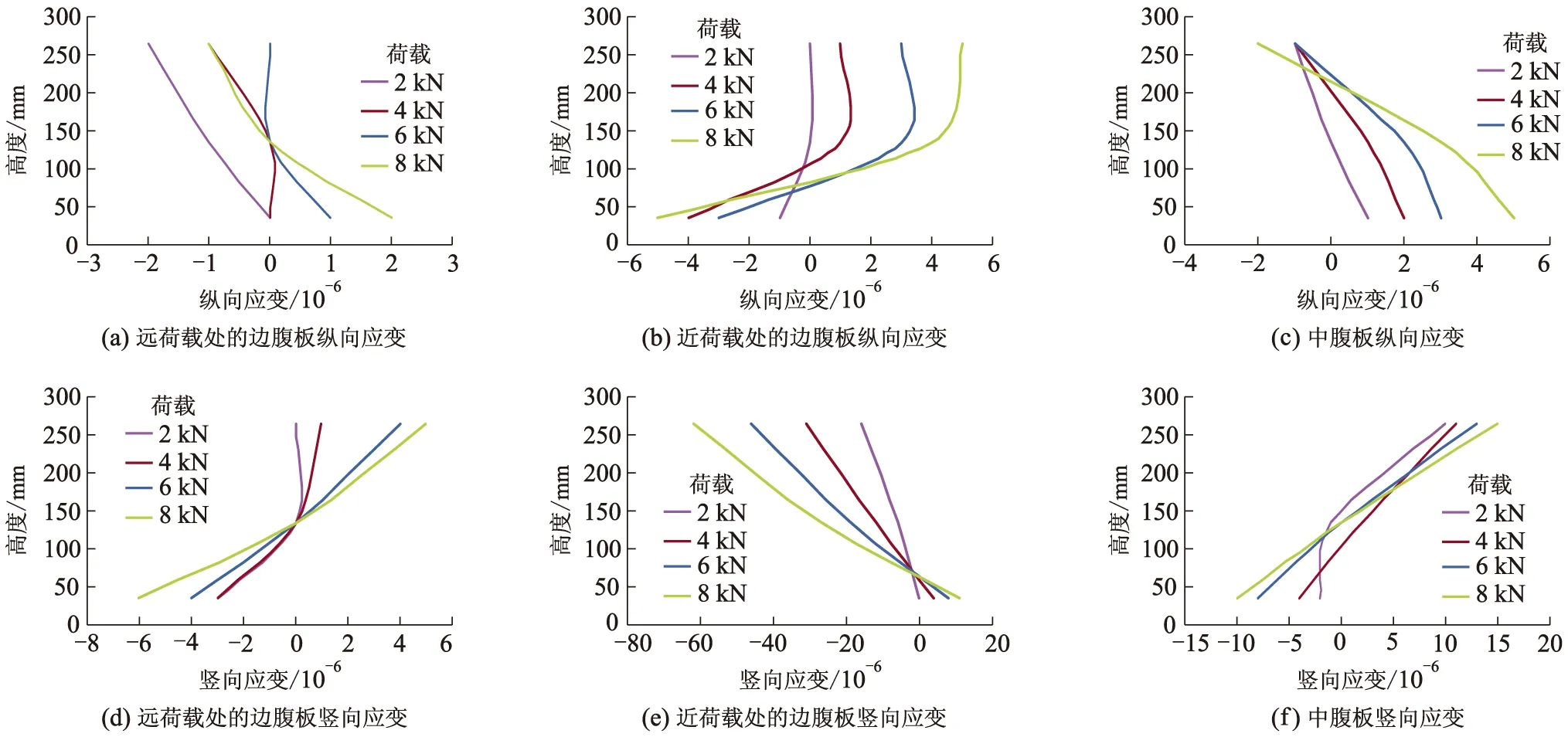
图6 试验梁腹板在翼缘端部加载下纵、竖向应变曲线
针对腹板竖向应变,同一荷载在两种工况下的中腹板和距离荷载较远处边腹板的竖向应变随高度变化的趋势一致,两者同一高度时的应变较接近,但是中腹板竖向应变大于远离荷载的边腹板竖向应变,与近荷载处的边腹板竖向应变数值正负相反.近荷载的边腹板随着荷载向翼缘端部移动,随着高度增加竖向压应变绝对值越来越大.
针对腹板纵向应变,在两种工况下远离荷载的边腹板纵向应变,随着高度的降低压应变逐渐转化为拉应变.
针对近荷载的边腹板纵向应变,腹板间加载时,沿腹板高度方向均为拉应变.悬臂翼缘端部加载,腹板上缘均为拉应变,腹板下缘均为压应变.
通过对波形钢腹板单箱双室箱梁腹板的纵、竖向变形分析,明确了波形钢腹板对混凝土桥面板的支撑状态.
2 单箱双室箱梁桥面板横向内力
表1为波形钢腹板单箱双室箱梁桥面板在工况Ⅰ下的跨中横向应力汇总.
表1中,有限元值为采用有限元软件ANSYS计算的横向应力值,试验值为本模型试验的横向应力测量值.

表1 工况Ⅰ下单箱双室箱梁桥面板横向应力汇总
图7为单点加载时跨中断面桥面板横向应力分布曲线.由表1可知横向应力试验值与有限元值较接近,进一步证实图7中桥面板横向应力分布曲线的正确性.

图7 单点加载时跨中断面桥面板横向应力分布曲线
3 线刚度比对桥面板横向内力的影响
以工况Ⅰ为例,进一步研究上述结构的腹板与顶板线刚度比变化对顶板横向内力产生的影响.在试验梁尺寸基础上变换腹板高度,采用有限元法进行参数分析,荷载作用位置处的桥面板横向内力汇总见表2,表中线刚度比指的是中腹板与顶板线刚度的比值.其中试验梁的腹板与顶板的线刚度比为0.116.
图8为根据表2数据绘制的试验梁顶板横向内力随线刚度比的变化曲线.

表2 工况Ⅰ下不同线刚度比时桥面板横向内力汇总
由图8可知:波形钢腹板单箱双室箱梁的混凝土顶板横向内力随腹板与顶板线刚度比变化基本呈直线变化;随着腹板与顶板线刚度比增加,顶板的横向内力随之减小.
笔者在之前的研究中,针对波形钢腹板单箱单室箱梁总结出了腹板与顶板的线刚度比m与桥面板内力M的关系式,将线刚度比对桥面板横向内力的影响以数值的形式表现出来,以此来表达腹板对桥面板的支撑特点.关系式如下所示:
(1)

总之,无论单箱单室波形钢腹板还是单箱双室波形钢腹板,在波形钢腹板箱梁截面上腹板间距确定时,波形钢腹板与混凝土顶板的线刚度比是影响桥面板横向内力的重要因素,且变化规律相同.
4 结 论
1) 为研究波形钢腹板箱梁的腹板受力性能、桥面板横向受力特性及其相互关系,通过对一片波形钢腹板单箱双室模型梁的弹性阶段试验,针对波形钢腹板的纵、竖向变形进行了分析,可知边腹板和中腹板的变形特征,中腹板与边腹板在变形上的差异及其对桥面板支撑状况的不同.
2) 无论单箱单室波形钢腹板箱梁还是单箱双室波形钢腹板箱梁,其腹板对顶板的约束程度直接影响到顶板的横向受力,顶板横向内力随腹板与顶板线刚度比变化基本呈线性变化.

