基于离线模型参数修正的结构混合试验方法

郭玉荣，陈 凡

(1.湖南大学 土木工程学院，湖南 长沙 410082; 2.建筑安全与节能教育部重点实验室，湖南 长沙 410082)

子结构拟动力试验方法又称为结构混合试验方法，是目前结构地震响应模拟中常用的方法[1-4]。该方法将结构中难以进行数值模拟的部分取出来作为试验子结构(或称为物理子结构)在实验室进行加载试验，其余部分作为数值子结构在计算机上进行模拟，从而使得在有限的试验设备条件下可以开展大比例的结构地震响应模拟，具有较高的经济性。此外，通过互联网将异地的试验设备进行联网试验，又形成了结构远程协同混合试验方法[5-7]。

结构混合试验方法的出发点是为了提高结构地震响应时程分析的模拟精度，因此其主要目的是获取结构体系在系统层次上的地震响应[8-9]，而不是试验子结构的局部破坏特征，后者可以用预定加载路径的拟静力试验方法来获取，具有更高的试验效率。当结构中的构件数量较少，传统的结构混合试验方法可以获取较高的模拟精度。然而在构件数量较多的建筑结构里面，取单个构件甚至局部结构作为试验子结构进行传统混合试验，对于提高结构系统层次地震响应模拟精度相对有限。为了克服这个不足，研究者提出了在线模型更新结构混合试验方法[10-14]。该方法假定数值子结构与物理子结构具有相同的恢复力模型参数，在试验过程中利用物理子结构的试验观测数据，在线识别子结构模型参数，同时实时更新数值子结构模型参数，以提高混合试验数值模拟精度。

基于在线模型更新混合试验方法的基本思想，对于试验子结构的恢复力特性受加载路径影响较小的情况，或者数值子结构与试验子结构具有接近的加载路径的情况，本文提出一种离线模型参数修正结构混合试验方法。该方法除了能有效提高传统结构混合试验方法的模拟精度之外，还具有较高的试验效率。

1 离线模型参数修正结构混合试验方法的基本思想

在结构混合试验中，整体结构被划分成两部分：即物理子结构和数值子结构。物理子结构的力和位移关系通过试验实测得到，数值子结构的力和位移关系则通过数值模拟来获取。

图1(a)显示了传统结构混合试验方法的基本思想。在混合试验开始之前，需要根据整体结构情况确定试验子结构，再根据试验子结构在整体结构中的约束情况和实验室设备加载能力，确定实际加载的简化边界条件。结构混合试验中，每求解一次运动方程，就将计算得到的试验子结构位移发送给试验设备控制系统进行加载，然后将实测的试验子结构恢复力返回给运动方程进行下一步求解，数值子结构则根据选定的滞回模型和模型参数计算恢复力。这种传统的结构混合试验方法适用于构件数量较少的结构，比如桥梁结构，取作试验子结构的部分具有数值模拟困难和独特性的特点，通过混合试验可以明显提高结构地震响应的模拟精度。

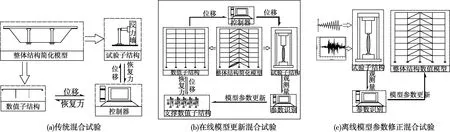
图1 结构混合试验方法示意图Fig.1 Schematic of structural hybrid test method

对于同类构件较多的结构，比如多层多跨框架结构，图1(b)的在线模型更新混合试验方法增加了对试验子结构实测数据进行参数识别并更新同类数值子结构模型参数的功能，从而提高结构地震响应模拟精度。这个方法的基本假定是同类数值子结构与试验子结构具有相同的受力特征，且忽略加载路径对模型参数影响。目前在线模型更新结构混合试验方法主要研究有效的参数识别算法，以及如何在构件、截面和材料等不同层次上进行模型参数识别和更新[15]。

基于在线模型更新混合试验方法的基本思想，本文将整体结构地震响应求解过程和试验子结构的加载试验分离成独立的2部分，称为离线模型参数修正混合试验方法。如图1(c)所示，该方法的实现流程如下：(1)对整体结构特征进行分析，决定是否要进行混合试验。然后从整体结构中选出难以进行数值模拟的部分作为试验子结构，并确定加载边界条件；(2)采用构件恢复力模型参数初始值对整体结构进行地震响应时程分析，从中提取试验子结构的位移响应时程作为其加载路径，或者直接按拟静力试验方法确定试验子结构的加载路径；(3)按设定的加载路径，对试验子结构进行拟静力加载试验，获取完整的实测滞回曲线；(4)基于实测的试验子结构滞回曲线，进行恢复力模型参数识别；(5)将识别的恢复力模型参数赋予试验子结构和同类数值子结构，采用通用有限元软件对整体结构进行地震响应时程分析。

以图2所示的带支撑框架结构混合试验为例，取支撑A为试验子结构，其余部分为数值子结构。对比2种模型更新混合试验方法如下：(1)在线模型更新混合试验中，每求解一步运动方程得到支撑A的位移，就将位移加载给试验子结构支撑A获取其恢复力，然后进行模型参数识别，用识别的参数更新其它3根支撑的模型参数，再进行下一步运动方程求解。(2)离线模型参数修正混合试验中，先设定位移加载路径直接对试验子结构支撑A进行拟静力加载试验，获取支撑A完整的滞回曲线后进行模型参数识别，再将识别的参数赋给全部的支撑(包括试验子结构支撑A)，之后即可多次进行整体结构在不同地震激励下的响应模拟。

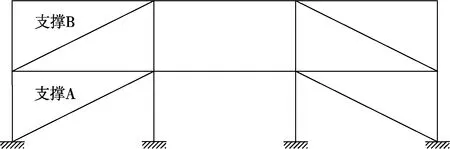
图2 约束屈曲支撑框架Fig.2 Steel frame with BRBs

2 试验子结构模型参数识别

模型更新混合试验中，试验子结构模型参数识别的准确性是影响结构混合试验精度的重要因素。为此，需要选择能有效描述试验子结构受力特征的恢复力模型和合适的参数识别算法。目前常用的参数识别方法有最小二乘法、卡尔曼滤波器(KF)、扩展卡尔曼滤波器(EKF)、无迹卡尔曼滤波器(UKF)、粒子滤波器等，但是在非线性系统参数辨识领域最常用是UKF方法。这里选用UKF方法来对比不同加载路径下试验子结构模型参数识别精度和收敛过程。取约束屈曲支撑(BRB)为试验子结构，采用Bouc-Wen恢复力模型描述BRB的恢复力特性，且假设已知模型参数的真实值。

试验子结构来自图2所示2层3跨钢框架结构中的约束屈曲支撑A和B。该框架层高3 m，跨度6 m，框架梁、柱均采用Q345H型钢，其截面尺寸及材料特性见表1，支撑的截面尺寸及材料的力学特性见表2。

BRB构件的恢复力采用Bouc-Wen模型来描述，按公式(1)、(2)计算，

f(d)=αkd+(1-α)kz.

(1)

(2)

式中：f(d)为支撑恢复力；k为初始刚度；d为实际位移；z为滞变位移；v为速度；α为屈服后刚度比；n为控制滞回光滑程度的参数；β和γ为控制滞回环形状与峰值的参数。

表1 梁、柱的截面尺寸及力学特性Table1 Dimensionsandmechanicalpropertiesofbeamsandcolumns型号截面积/mm2弹性模量/105MPa屈服强度/MPa柱HM400×300×10×16132802.1345梁HM450×300×11×18153542.1345表2 BRB基本参数Table2 ParametersofBRB截面积/mm2构件长度/mm弹性模量/105MPa屈服强度/MPa第二刚度比25006708.22.12350.02

Bouc-Wen恢复力模型参数真实值取k=78 000 kN/m，β=70，γ=60，α=0.02，n=1。采用UKF 算法识别Bouc-Wen 恢复力模型参数的相关方程和参数初值设定如下：

(1)针对Bouc-Wen恢复力模型待识别的5个参数，确定非线性系统的状态向量：

x=[x1,x2,x3,x4,x5,x6]=[z,k,β,γ,n,α].

(3)

(2)其连续状态方程表达为：

(4)

(3)采用欧拉折线法将状态方程离散为：

(5)

(4)写出离散观测方程：

yk+1=h(xk+1,uk+1)+wk+1=x6,k+1x2,k+1dk+1+(1-x6,k+1)x2,k+1x1,k+1+wk+1.

(6)

(5)将状态初始估计值设为：

(7)

(6)设初始状态估计误差协方差为：

P0=diag([1e-8,1e8,1e3,1e3,1e-3,1e-2]).

(8)

(7)设过程噪声协方差矩阵为：

Q=diag([1e-10,0,0,0,0,0]).

(9)

设观测噪声协方差R=700 kN2。

为了考察结合具体恢复力模型的参数识别算法的识别精度、收敛速度和稳定性，以及基于不同加载路径下获取的试验子结构滞回曲线所识别的模型参数是否一致，这里采用数值仿真方法来模拟混合试验过程。相对于采用真实混合试验方法，数值仿真方法简单易行，能排除试验各种偶然因素的影响，更便于考察识别算法的性能。首先假定一组Bouc-Wen恢复力模型参数真实值，假设该真实值能非常精确地描述试验子结构的恢复力特性，用这组真实值计算不同加载路径下试验子结构的滞回曲线作为实测滞回曲线，后续称为参考滞回曲线。在开始试验之前，给数值子结构设定有一定误差的模型参数，该组参数称为初始值，而通过试验子结构参考滞回曲线进行参数识别得到的模型参数称为识别值。用参数初始值和识别值计算得到的滞回曲线分别称为初始滞回曲线和识别滞回曲线。

采用3种不同加载路径工况下模拟的试验子结构滞回曲线作为参考滞回曲线，其中工况A和工况B的加载路径来自图2所示框架中支撑A和B的地震位移响应时程，工况C则取低周反复位移加载作为加载路径，3种工况的加载路径如图3所示。图2所示的框架结构时程分析采用OpenSees来模拟，输入地震波为EL Centro波，为了加大支撑的非线性位移，地震加速度峰值设为7.17 m/s2，时间间隔为0.01 s，总时长为20 s。数值积分算法采用Newmark法求解，其中γ=0.5，β=0.25。

图3 3种工况下支撑A的加载路径Fig.3 Loading paths of brace A under three loading conditions

图4显示了3种工况下试验子结构的识别滞回曲线、初始滞回曲线和参考滞回曲线的对比情况。由于恢复力模型参数初始值存在误差，初始滞回曲线与参考滞回曲线之间存在较大的差异。而在3种加载路径工况下，识别滞回曲线与参考滞回曲线的吻合程度大大提高。

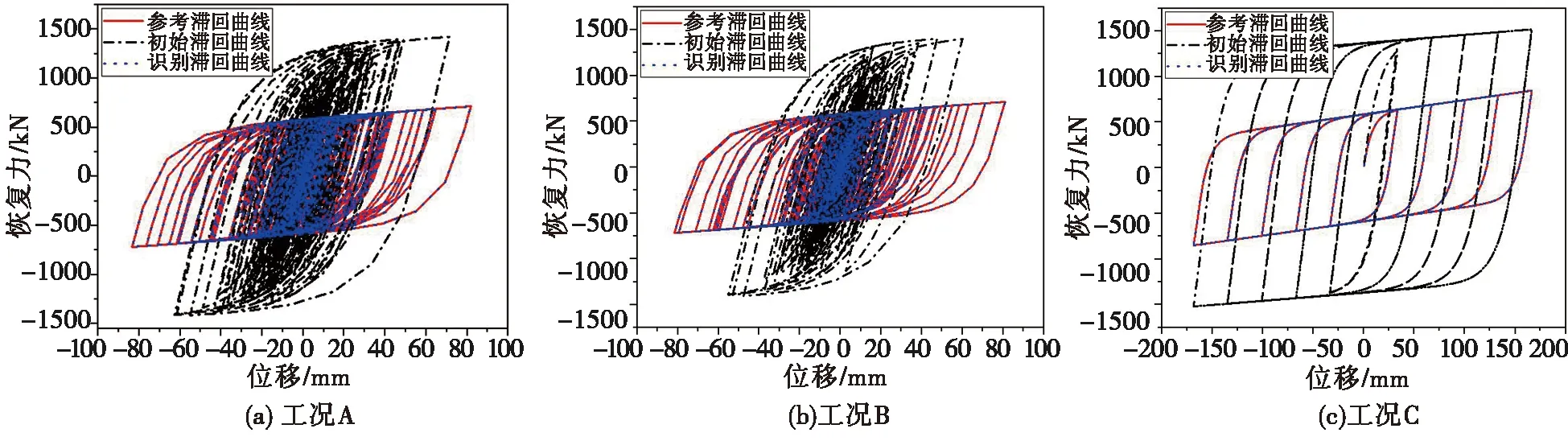
图4 3种工况下支撑A的滞回曲线Fig.4 Hysteresis curves of brace A under three loading conditions

试验子结构各个工况的模型参数识别值及相对误差如表3所示，不同工况模型参数的识别值与真实值之间的误差都比较小，或者说都能有效地识别出模型参数，原因是用Bouc-Wen恢复力模型模拟的支撑滞回特性受加载路径的影响非常小。

表3 支撑A的参数识别值及相对误差Table 3 Identification values of parameters and relative errors for brace A

试验子结构各工况模型参数识别过程曲线对比如图5所示。在不同加载路径下，虽然各参数识别过程曲线有所差异，但最终都能够逐渐收敛到真实值附近。同时也可以看到，不同工况的参数识别收敛速度也不相同，主要和试验子结构的加载路径有关。相较于从地震响应时程分析得到的工况A和B，低周反复位移加载工况C的参数识别收敛速度更快，其原因是工况C在前期加载的位移幅度比工况A和B明显大一些。从图3的位移加载路径来看，在第6 s前工况A和B的位移未超过11 mm，工况C的位移已经达到67 mm。参照对比图4的滞回曲线可见，相应于第6 s前的工况A和B基本上处于弹性状态，而工况C已经进入了明显的非线性状态。对比图5的参数识别过程曲线可见，在第6 s前，由于工况A和B基本处于弹性状态，与非线性相关的模型参数识别值离真实值较远，而工况C由于较早进入非线性状态，因此收敛速度明显快于工况A和B。

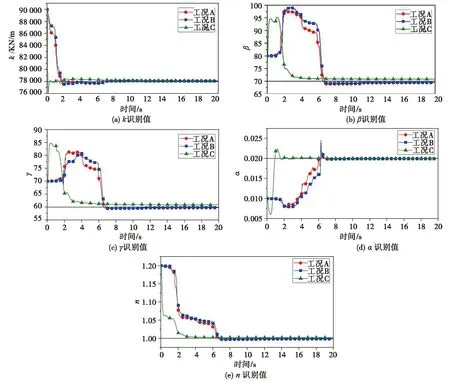
图5 Bouc-Wen模型参数识别过程曲线Fig.5 Time history of identification parameters of Bouc-Wen model

3 整体结构模拟验证

以BRB的钢框架结构为例，通过对比传统混合试验、在线模型更新混合试验、离线模型参数修正混合试验和OpenSees 纯数值分析结果来考察本文方法的模拟精度。

3.1 结构模型

选取如图6所示的一榀8层4跨带BRB的钢框架结构进行地震响应模拟对比。该钢框架层高3 m，跨度6 m。框架梁、柱均采用Q345H型钢，梁、柱的截面尺寸及力学特性如表1所示，支撑的截面尺寸及力学特性如表2所示。采用OpenSees模拟整体结构地震响应和试验子结构的力-位移关系，其中BRB采用twoNodeLink单元，其力-位移关系用经典的Bouc-Wen非线性恢复力模型模拟。梁、柱采用nonlinearBeamColumn单元进行模拟，其截面用Aggregator命令考虑轴力弯矩耦合，弯矩-曲率关系采用Steel01双折线模型，具体参数见表4，轴向力-位移关系取Elastic弹性模型，其具体参数见表5。框架梁上的分布荷载为34.23 kN/m，输入地震波为El Centro波，地震加速度峰值为1.43 m/s2，时间间隔为0.01 s，总时长为20 s。

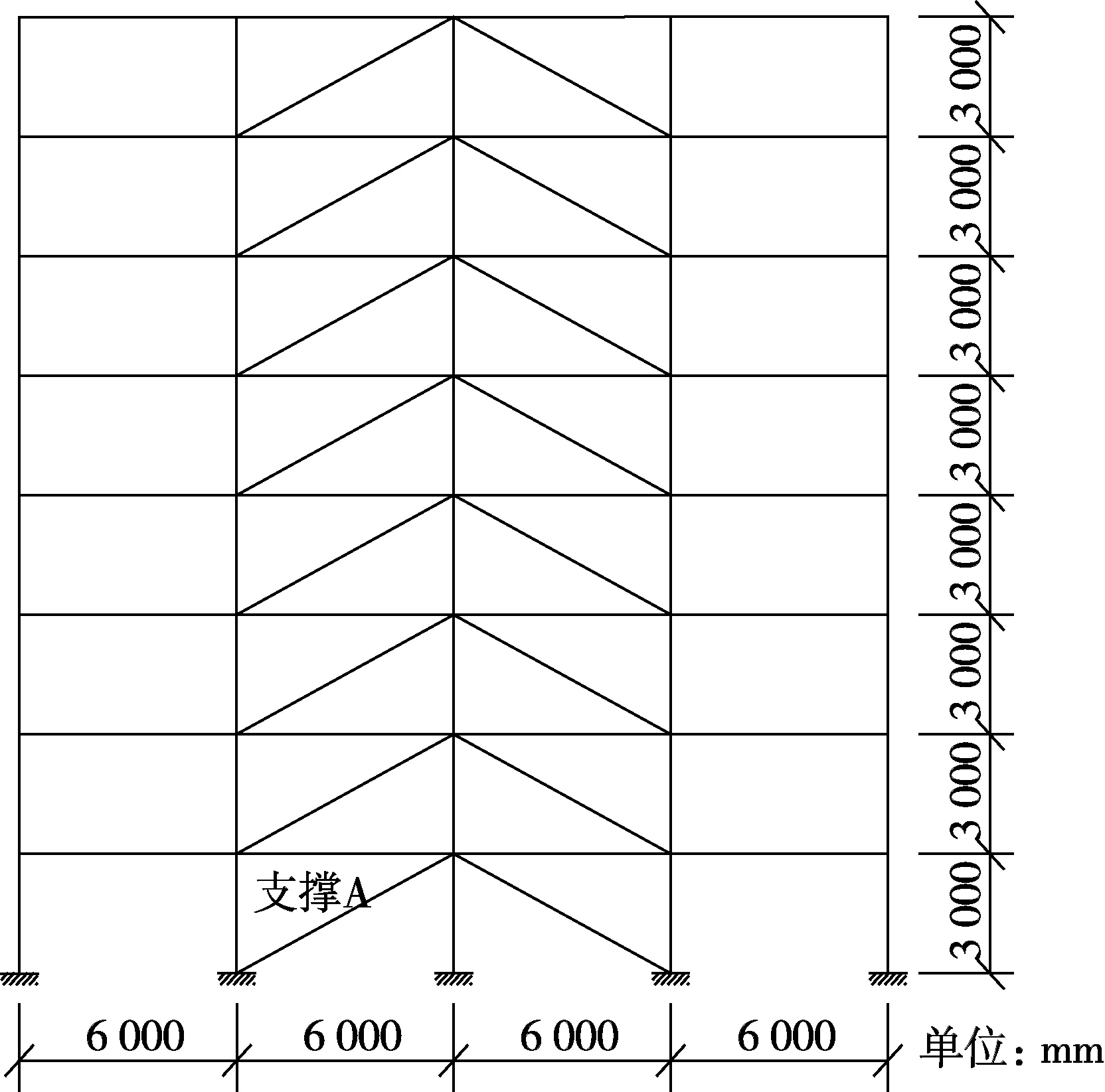
图6 带BRB的钢框架立面图Fig.6 Elevation of the steel frame with BRBs

表4 Steel01模型参数Table4 Steel01modelparameters屈服弯矩/(kN·m)抗弯刚度/(kN·m2)b柱8801122000.01梁690778000.01注:b为双线性模型的屈服后刚度与弹性刚度比。表5 Elastic模型参数Table5 Elasticmodelparameters截面积/mm2弹性模量/105MPa柱157402.1梁136702.1

3.2 混合试验模拟结果对比

为了对比不同混合试验方法对整体结构地震响应的模拟精度，先拟定结构地震响应的参考值。Bouc-Wen恢复力模型参数真实值取k=78 000 kN/m，β=70，γ=60，α=0.02，n=1，所有BRB采用模型参数真实值进行结构地震响应时程分析得到的结果作为参考值。虚拟混合试验取图6所示钢框架中的支撑A作为试验子结构，采用模型参数真实值在OpenSees中进行数值模拟来代表试验实测值。

进行对比的3种混合试验工况如下：(1)HYT：传统结构混合试验，其数值子结构中的BRB恢复力模型参数采用第2节的初始估计值；(2)OnHYT：在线模型更新结构混合试验，通过试验子结构的滞回曲线来识别恢复力模型参数，并实时更新数值子结构BRB的模型参数；(3)OffHYT：本文离线模型参数修正混合试验，先对试验子结构BRB进行低周反复拟静力试验获取滞回曲线，再进行恢复力模型参数识别，最后用识别参数修改结构中所有BRB的恢复力模型参数进行整体结构时程分析。

图7显示了3种混合试验得到的结构顶点位移时程曲线和参考值之间的对比，从中可见传统的结构混合试验HYT由于只进行一个BRB实测试验，与参考值偏离较大，而考虑模型更新的混合试验OnHYT和OffHYT与参考值吻合较好，说明通过参数识别和模型更新能有效提高整体结构地震响应的模拟精度。

图7 结构顶层位移时程曲线Fig.7 Time history of top story displacement

图8显示了楼层侧移包络线对比，与HYT相比，OnHYT和OffHYT的模拟精度明显提高。为了比较OffHYT和OnHYT与参考试验之间的误差，采用公式(10)的无量纲统计指标均方根偏差(Root Mean Square Deviation，RMSD)予以统计，其层间位移角误差RMSD如图9所示。

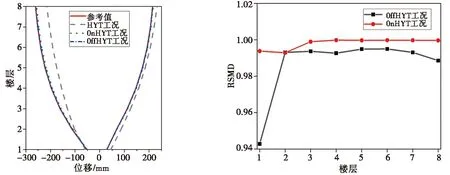
图8 楼层侧移包络图 图9 层间位移角误差RMSDFig.8 Lateral displacement envelope Fig.9 RMSD of drift angle

(10)

从图9可以看出，2种模型更新混合试验的层间位移角误差RMSD均较小，但是OffHYT的误差比OnHYT相对稍小，其原因是该混合试验所选择的恢复力模型能完全描述试验子结构的特性，OnHYT方法在获得比较准确的参数识别值之前，其数值子结构BRB仍然采用参数初始值模拟，而OffHYT在时程分析一开始，所有BRB都采用了最终的参数识别值来模拟。

4 结构混合试验精度和效率讨论

结构混合试验的主要目的是提高整体结构在系统层次上的地震响应模拟精度。由于结构中某些部分数值模拟误差较大，或根本没有合适的模型进行数值模拟，所以将其取出来作为试验子结构进行实测试验，从而避开该部分数值模拟的困难。但同时也可以看到，这种混合试验方法一般适用于试验子结构具有唯一性的特点，即结构中没有和试验子结构完全相同的同类数值子结构。否则，因试验子结构实测试验对整体结构模拟精度的提升会随着同类数值子结构规模的增加而逐步降低，最后失去混合试验的意义。

在线模型更新混合试验和本文的离线模型参数修正混合试验，都试图通过对试验子结构的实测数据进行参数识别来提高同类数值子结构的模拟精度，进而提高整体结构的模拟精度。实现这个目标的前提条件是有能描述试验子结构滞回特性的恢复力模型且识别的模型参数比较准确。从模拟精度对比的角度来说，这2种混合试验之间的差异主要有2个方面：(1)离线模型参数修正混合试验的试验子结构也采用识别的模型参数进行数值模拟，与在线模型更新混合试验相比，损失了一定的精度。但是，这一损失的精度会随着同类数值子结构规模的增加逐步减弱，最后两种混合试验的精度趋向一致；(2)离线模型参数修正混合试验中，所有数值子结构全程都采用最终的参数识别值来模拟，而在线模型更新混合试验在获得比较准确的参数识别值之前，其数值子结构仍然采用参数初始值模拟，模拟精度较前者低。也有学者尝试在某一步获取识别的参数后，从零时刻开始重新进行时程分析，到当前时刻再继续混合试验。这种处理方法类似于“重启动”试验，其模拟精度比本文方法高，但是数值模拟的时间会大幅度加长。

在线模型更新混合试验是一种难度比较大的试验，需要数值模拟、结构加载试验、模型参数识别和模型更新等各个方面协同工作才能完成，试验程序开发的难度比较大。模型参数识别精度往往受参数初始值误差、初始协方差的影响，初始值选择不当可能会产生较大的识别误差甚至失稳。试验中出现故障的概率也相对较高，为此可靠的在线模型更新混合试验程序还需要包含续航试验功能[16]。离线模型参数修正混合试验只需要对试验子结构进行循环加载的拟静力试验，试验程序开发只涉及模型参数识别，相对比较简单。由于是获取完整的滞回曲线后进行参数识别，识别初始值选择不受试验限制，识别精度和稳定性相对有保障。由于试验和数值模拟分离，可以从整体结构中取出多个不同类型的试验子结构在不同的实验室进行实测试验，实现协同试验。获取识别参数后，可以对结构进行任意多次地震响应模拟，试验数据的利用率较高。

5 结论

本文提出了一种基于离线模型参数修正的结构混合试验方法，与在线模型更新混合试验方法类似，该方法可应用于结构中存在多个同类数值子结构且滞回特性受加载路径影响较小的结构混合试验。

(1)与传统的结构混合试验方法相比，本文方法可以有效提高结构地震响应模拟精度。当选择的恢复力模型能有效地描述试验子结构特性时，本文方法与现有的在线模型更新结构混合试验精度接近。

(2)本文方法将结构混合试验拆分成子结构拟静力试验、模型参数识别和整体结构地震响应模拟3个独立的部分，降低了试验难度且提高了混合试验的稳定性。

(3)由于将试验和数值模拟分离，本文方法对试验数据的利用率相对较高，总体上提高了试验效率。