随机场-贝叶斯方法应用于非饱和土边坡稳定性可靠度分析

宗振邦，王长虹，孙德安

(上海大学 力学与工程科学学院 土木工程系，上海 200444)

季节性强降雨和水位变化是诱发库区滑坡的主要外因[1]。意大利的Vajont滑坡就是由降雨和库区水位上升触发滑坡的典型案例[2]。自2003年三峡库区首次蓄水以来，许多历史上已经稳定的老滑坡再次被激活，并逐渐发展成新的地质灾害[3]。目前，滑坡监测预警系统虽然被广泛应用[4]，但对历史上稳定的老滑坡进行新的灾害预测还是非常困难。

地层岩土特性、构造和水文条件以及地形地貌等是形成滑坡的内在因素[5-6]。边坡岩土体由于矿物构成、沉积变质、风化侵蚀以及其它地质作用，岩土参数普遍存在较大的空间变异性，不仅影响边坡的变形、应力和孔隙水压等，对边坡破坏模式和失效概率也有重要影响[7]。另一方面，边坡土体的饱和-非饱和状态和渗透特性对边坡稳定性也具有较大影响[8]。

Griffiths和Fenton[9]提出了岩土参数随机有限元法，Srivastava等[10]在渗流分析中将渗透系数作为对数正态随机场，研究了边坡的稳定性。Cho[11]讨论了渗透系数的空间变异性对残积土边坡降雨入渗破坏模式的影响。Cai等[12]分析了地下水补给过程中，渗透系数和抗剪强度的空间变异性对边坡稳定性的影响。李典庆等[7]提出了考虑土体参数空间变异性的边坡可靠度分析非侵入式随机有限元法，极大地提高了计算效率，为解决复杂边坡稳定可靠度问题提供了一条有效的途径。

以上研究仅考虑了岩土参数为多元随机变量或单变量随机场，本文在单变量随机场基础上，将边坡的关键岩土参数(有效黏聚力、有效内摩擦角、杨氏模量和饱和渗透系数)定义为空间统计相关的多元随机场变量，采用随机场-贝叶斯方法系统地融合岩土参数的先验分布、钻孔勘察数据和长期监测数据，从而更加精确地校准岩土参数的后验分布。将该方法应用于三峡库区石榴树包特大滑坡，并进行考虑渗流的非饱和土边坡稳定性分析以及灾害预测，具有较大的现实意义和工程实用价值。

1 非饱和土边坡稳定分析理论

考虑渗流的非饱和土边坡稳定分析理论分为3个基本部分：(1)边坡降雨入渗和库区水位波动作用下的瞬态渗流分析；(2)非饱和土的有效抗剪强度分析；(3)非饱和土边坡稳定性分析。

1.1 瞬态渗流分析

Richards提出了非饱和土孔隙水瞬态流动的控制方程，为了求解孔隙水压分布，需要提供土水特征曲线(Soil-Water Characteristic Curve, SWCC)和基质吸力-渗透系数关系曲线(即水力传导函数，Hydraulic Conductivity Function, HCF)。采用V-G模型[13]描述SWCC和HCF，具有物理意义明确，参数简单的特点，公式如下：

(1)

式中，Θw表示归一化的体积含水量；θs是饱和体积含水量；θr是残余体积含水量；α、m和ns表示土水特征曲线的拟合参数，m=1-1/ns；ks为饱和渗透系数。

1.2 非饱和土抗剪强度分析

为了深入分析岩土参数的空间变异性，暂不考虑黏聚力，内摩擦角和杨氏模量随基质吸力的变化，仅考虑了渗透系数的非饱和变化特征，因此，非饱和土边坡的抗剪强度可以简化为：

τf=c′+(σ-ua)tanφ′+Θw(ua-uw)tanφ′.

(2)

式中，τf为抗剪强度，c′为有效黏聚力，φ′为有效内摩擦角，σ为总应力，ua为孔隙气压，uw为孔隙水压，基质应力σs=-Θw(ua-uw)。

1.3 非饱和土边坡稳定性分析

采用Morgenstern-Price极限平衡法[14]计算边坡安全系数Fs，公式如下：

(3)

式中，Wi为土条i的自重，Xi-1和Xi为土条i水平条间力，Yi-1和Yi为土条i竖向条间力，αi为土条i的边坡倾斜角，li为土条i的滑弧长度。

2 随机场-贝叶斯方法

在非饱和土边坡稳定分析理论中，关键岩土参数的空间变异性对边坡的稳定性具有显著影响。因此，随机场-贝叶斯方法将关键岩土参数视为统计相关的多元随机场变量ψ(x)。利用贝叶斯理论融合先验知识、钻孔勘察数据和长期监测数据，对岩土参数的空间统计特征进行动态校准，然后利用更新后的岩土参数开展边坡稳定性分析。

2.1 随机场理论

根据获取岩土参数的途径，随机场-贝叶斯方法中定义了两种类型的数据：直接数据za(如钻孔勘察数据)和间接数据zb(如长期监测数据)，误差为εa，εb。

随机场理论在随机变量的基础上，采用平均值μ和标准差v，描述了整体的随机性，并使用自(协)相关函数ρi,j(h), (i,j=1,...m)描述岩土参数的空间变异性[15]，m为岩土参数的数量：

(4a)

(4b)

式中，h表示随机场的滞后距，并假定ρi,j(h)=ρj,i(h)。

在理论变异函数中，球状变异函数具有简洁性和鲁棒性，因此可应用于岩土参数的空间变异性描述：

(5)

式中，a1表示主变程。

三维随机场的空间各向异性可以通过加权滞后距描述[16]：

(6)

式中，变程比率η1=1.0(假定主变程a1方向与边坡面平行)；η2为第二变程a2(主滑坡面内与a1垂直的方向)除以a1的结果；η3为第三变程a3(分别与a1和a2垂直的方向)除以a1的结果。

2.2 贝叶斯方法

贝叶斯方法利用条件概率理论，将融合先验信息p(ψ)，钻孔勘察数据za和长期监测数据zb，推断多元岩土参数随机场变量ψ(x)的后验分布p(ψ|za,zb)。

(7)

式中，p(ψ)为多元随机场变量的先验联合概率密度函数，似然概率函数L(zb|ψ,za)为长期监测数据zb基于多元随机场变量ψ(x)和钻孔勘察数据za的函数，后验分布p(ψ|za,zb)则是多源数据信息融合校准的结果。

2.3 后验抽样算法

贝叶斯方法仅在极少数情况下可以获得后验分布的理论概率密度函数。因此，随机场-贝叶斯方法采用抽样算法来获得数值解，算法由构建先验分布、计算似然函数概率和统计后验分布三部分组成，如图1所示。

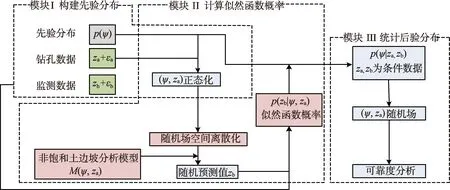
图1 随机场-贝叶斯方法数值分析程序Fig. 1 Numerical analysis procedures of SRFs based-Bayesian method

(1)构建先验分布

岩土参数通常可以表示为对数正态多元随机场变量ψ(x)，先验概率分布p(ψ)描述了m个岩土参数在随机场n个离散点的空间统计特征[17-18]。

(8)

式中，随机场协方差矩阵C=Rn⊗Cm，Cm为m个正态分布随机变量的协方差矩阵；在此基础上，矩阵Rn由自(协)相关系数ρi,j(h)，(i,j=1,...m)组成，“⊗”为矩阵叉乘符号。

(2)计算似然函数概率

似然概率函数的计算需要进行随机场离散化和非饱和土边坡有限元数值模拟。通用驱动程序依靠控制文件和输入、输出函数配置数值分析过程，提供贝叶斯技术框架与计算软件GeoStudio2012之间的接口，利用命令流执行边坡稳定性数值分析，从而得到边坡长期监测的预测结果。

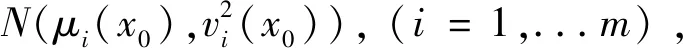
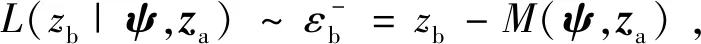
(9)

其中，Cεb为监测误差εb的协方差矩阵，εb之间的相关系数为ωij(i,j=1,...,k)，k表示长期监测数据zb的个数，可由监测点之间的欧氏距离[20]来定义：

(10)

式中，D(xbi,xbj)为两个监测点bi,bj之间的距离，maxD为所有监测点之间的最大距离。

(3)统计后验分布

非饱和土边坡有限元计算将耗费大量计算资源，为提高计算效率，利用马尔可夫链蒙特卡罗(MCMC，Marcov-Chain Monte-Carlo)模拟方法快速求解[21]。给定岩土参数随机场先验分布p(ψ)，通过随机分析M(ψ,za)，计算L(zb|ψ,za)。抽样系数定义为：

(11)

并从均匀分布u～U(0,1)中抽样一个ui，如果αi≥ui，接受ψi(x)作为后验样本；否则拒绝ψi(x)，及时调整先验概率函数p(ψ)的均值μ和协方差C，直至总抽样次数i=T。最后计算岩土参数的后验空间统计特征。

2.4 可靠度分析

根据随机场-贝叶斯方法校准关键岩土参数的后验分布p(ψ|za,zb)，并用于计算三峡库区历史老滑坡在夏季枯水位、强降雨条件下保持稳定的可靠指标。边坡安全系数Fs的极限状态函数表示为：

G=Fs-1=g(ψ)-1.

(12)

式中，Fs表示最危险滑动面的安全系数；g(ψ)表示最小安全系数的随机场极限平衡分析法。可靠指标为β=Φ-1[Pf(G≤0)]，Pf为G≤0相应的失效概率，算子Φ-1[·]表示标准正态累计函数逆运算。

利用响应面法可以有效地计算出随机变量可靠指标，但是，由于随机场变量存在一个空间离散化过程，因此随机场变量的可靠度分析不能再采用响应面法。本文将子集蒙特卡罗模拟(SMC，Subset Monte-Carlo simulation)算法[22-24]应用于边坡安全系数的随机场模拟，有效提高计算效率，进而计算失效概率和可靠指标。

3 案例研究

3.1 工程勘察资料

三峡库区石榴树包滑坡位于湖北省巴东新县城下游9.0 km的长江北岸，距离三峡大坝66 km，自1975年湖北省水文地质大队首次发现该滑坡以来，许多单位和学者对其进行过研究。图2为其地质剖面图，潜在滑坡体积为11.8×106m3，面积0.25 km2，宽度350～470 m，高程60-350 m，坡度25°～30°，ZK代表工程地质钻孔，PD代表勘探平洞；CK代表水文地质钻孔。

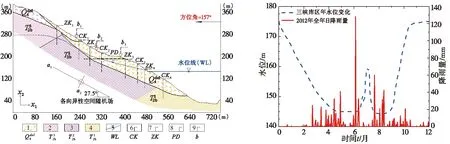
图2 石榴树包边坡地质剖面图 图3 非饱和瞬态渗流水力边界条件Fig.2 Geological profile of the Shiliushubao slope Fig.3 Hydraulic boundary conditionsfor the unsaturated transient seepage

表1是石榴树包滑坡岩土参数的原始勘察数据。三峡库区蓄水后，库区水位在145-175 m之间周期性波动，在滑坡表面设置了3个长期监测点，用于收集滑坡沉降以及水库水位的周期性波动和年降雨量，监测误差变异系数δb=0.1～0.3，如表2所示。图3为2012年度巴东县域日降雨量和三峡库区年水位变化，作为本文非饱和土边坡瞬态渗流分析的水力边界条件。土水特征曲线SWCC用基质吸力与体积含水量之间关系表示，如图4(a)所示。在随机模拟中，水力传导函数HCF将保持图4(b)的形状和参数，随机调整初始饱和渗透系数ks值。

表1 岩土参数的原始勘察报告Table 1 Original investigation report of geotechnical parameters

表2 滑坡表面长期监测数据Table 2 Long-term monitoring data on landslide surface

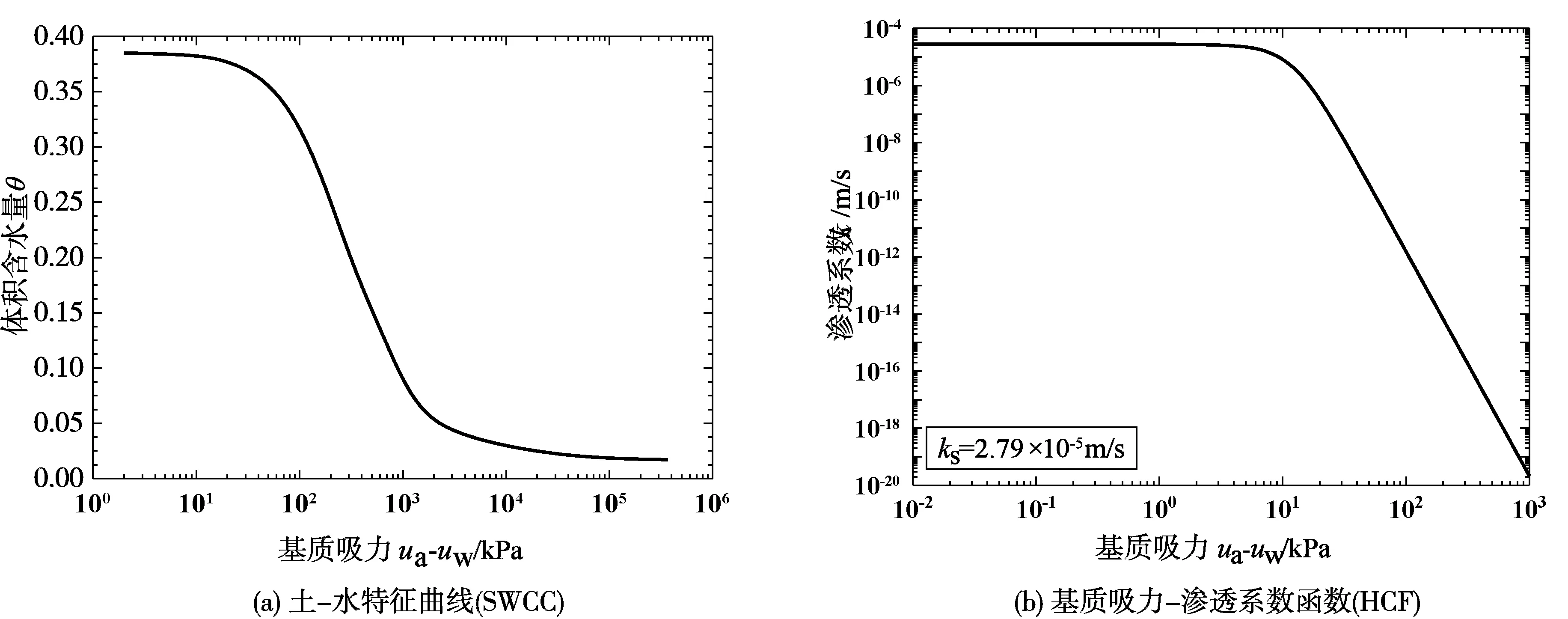
图4 非饱和土的水力特性Fig.4 Hydrogeological properties of unsaturated soil

3.2 岩土参数校准

(1)先验信息

表1中的岩土参数勘察数据无法提供多元随机场全面的统计数据，因此，将关键岩土参数c′,φ′,E,ks定义为多元随机场变量，先验概率边缘分布取为c′～LN(50,502)kPa，φ′～LN(40,402)°，E～LN(120,1202)MPa，ks～LN(4.0,4.02)m/d。主变程a1与坡面平行(倾角为27.5°)；第二变程a2垂直于边坡，a3垂直于坡面。假设a1和a2的值取为20 m。a3的初始变程比率取为0.2，即ηc′,3=ηφ′,3=ηE,3=ηks,3=0.2。

(2)数值分析

考虑渗流的非饱和土边坡稳定分析的有限元计算采用GeoStudio2012软件，二维有限元几何模型的长度为745 m，高度384 m；模型共划分4 605个节点和4 605个单元。其中，潜在滑坡体划分为3 730个随机单元，单元最大边长尺寸2.0 m，不大于第三变程a3=4m的一半，保证了离散化的随机场可以描述岩土参数的空间变异性。数值分析模型的边界条件：1)如图2所示，用SEEP/W模块分析非饱和土边坡渗流过程中，边坡前缘为水位和流量的混合边界，根据库区水位波动和日降雨入渗量确定；边坡后缘保持280 m的恒定水头；边坡底部设为不透水边界。2)在计算边坡遭遇夏天强降雨时，前缘为152 m的恒定水位和流量100 mm/d的混合边界，其他条件与上述边界相同。3)在SIGMA/W和SLOPE/W模块中，边坡后缘设为水平位移约束，底部基岩设为固定约束。

(3)后验分布

对联合先验分布p(ψ)进行1 000次马尔可夫链随机场离散化抽样和计算，统计关键岩土参数ψ=[c′,φ′,E,ks]的空间后验特征。以3个月为间隔，采用贝叶斯方法进行动态校准，关键岩土参数的第i次后验分布，作为第(i+1)次校准的先验知识，i=1,2,3。

基于前3个月的监测数据，讨论za、zb以及测量误差εa、εb对后验分布p(ψ|za,zb)的影响。存在以下6种情况：①具有较大不确定性的先验分布，即考虑za(δa=0.3)和zb(δb=0.3)；②不考虑钻孔勘察数据za，仅考虑监测数据zb(监测误差δb=0.1)；③考虑za(δa=0.1)和zb(δb=0.1)；④考虑za(δa=0.1)和zb(δb=0.2)；⑤考虑za(δa=0.1)和zb(δb=0.3)；⑥仅考虑一个监测点b1，za(δa=0.1)和zb1(δb1=0.1)。

以有效黏聚力c′为例，初始先验边缘分布p(c′)为LN(50,502)kPa，即变异系数δc′=1.0，具有较大的不确定性。通过融合钻孔勘察数据za和长期监测数据zb得到后验分布如图5所示。概率值较为显著的组合为③，后验边缘分布为LN(35.5,11.992)kPa，变异系数缩小为δc′=0. 34。不考虑钻孔勘察数据za的组合②变异系数较最优值增大1.16倍；组合⑥仅考虑一个监测点b1，较最优值增大1.15倍；6种组合中，组合⑤的误差最大，较最优值增大1.20倍不确定性。类似地，有效内摩擦角φ′、杨氏模量E和饱和渗透系数ks也得到相同的结论。因此，以下的讨论主要集中于组合③。如图6所示，有效黏聚力c′的后验均值在前3个月的监测数据组合校准后很快稳定下来，且小于先验分布的均值，标准差也呈下降趋势。基于监测数据组合③，经随机场-贝叶斯方法校准，得到后验分布c′～LN(35.1,4.282)kPa，变异系数δc′=0.122，大幅降低了岩土参数的不确定性。校准得到的其他岩土参数后验分布如表3所示。

图5 有效黏聚力的先验和后验分布 图6 有效黏聚力的均值和标准差变化Fig.5 Prior and posterior distributions of effective cohesion Fig.6 Mean and SD values of effective cohesion variation

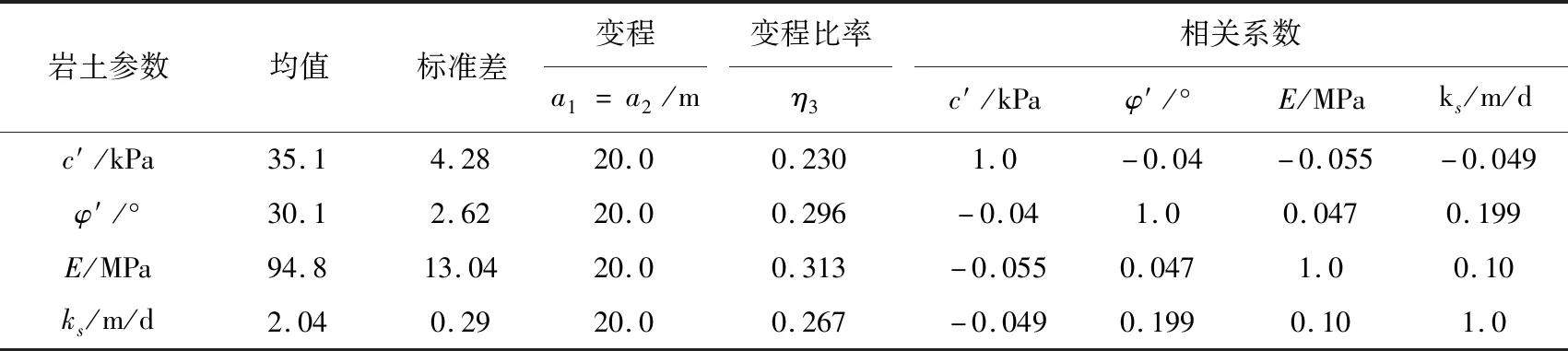
表3 多元随机场后验分布Table 3 Posterior distributions of the SRFs

(4)长期沉降验证

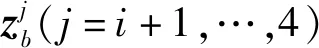
如图7所示，采用岩土参数有效黏聚力c′、有效内摩擦角φ′、杨氏模量E和饱和渗透系数ks的先验分布p(ψ)预测zb1，μzb1±vzb1可以包含实测值zb1，但具有较大的不确定性。采用前3个月的岩土参数校准值，对后期的监测数据进行预测，效果也不明显。然而，采用前9个月的监测数据校准得到岩土参数，再进行有限元计算，得到的预测值逐渐接近实测值，从而证明了随机场-贝叶斯方法的有效性。

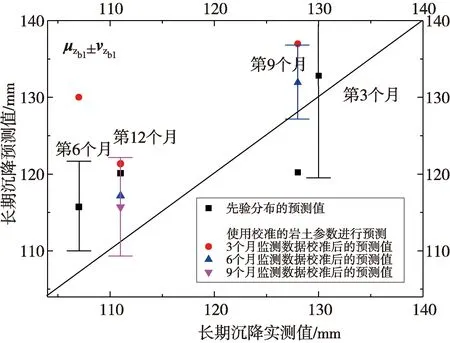
图7 实测和预测的长期监测数据zb1Fig.7 Measured and predicted long-term monitoring datazb1

3.3 边坡稳定性可靠指标分析

夏季的强降雨和水位变化是造成三峡库区老滑坡复活的重要因素，考虑这2个因素分析石榴树包边坡稳定性的可靠指标，分析时采用上述校准的岩土参数。需要说明的是，在边坡稳定性计算中，极限平衡法(如Morgenstern-Price法)不使用杨氏模量E。因此，在可靠度分析中只考虑有效黏聚力c′、有效内摩擦角φ′和饱和渗透系数ks的空间变异性。

与随机变量相比，将岩土参数视为随机场变量，可以给出更精确的滑动面和可靠指标。为了确定临界滑动面，在图8中，假定给ZK1和ZK2的钻孔勘察数据c′增加100 kPa，以提高该处的有效黏聚力，而临界滑移面#1(滑移半径=948.42 m)仅有20%的概率变成第二滑移面#2(滑移半径=468.13 m)，因此，可以认为临界滑移面#1控制着边坡的稳定性。

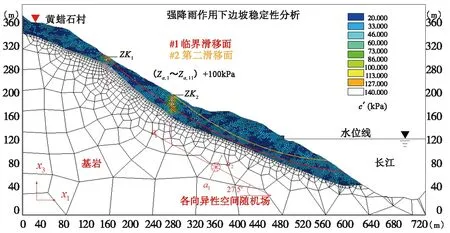
图8 随机场中有效黏聚力对临界滑动面的影响Fig.8 Effects of effective cohesion on critical sliding surface according to spatial random fields

以下将关键岩土参数分别假定为随机变量和随机场变量，三峡库区夏季平均水位为152 m，假定连续5天降雨，每天降雨量为100 mm情况下，计算边坡的安全系数和可靠指标。

(1)随机变量的可靠度分析

如图9(a)所示，采用后验均值c′=35.1kPa，φ′=30.1°和ks=2.04m/d计算8天内的边坡安全系数Fs值变化。经过连续5天降雨，Fs从最初的1.131急剧减小至第5天的1.055，边坡接近临界状态，滑移面#1半径为992 m(潜在滑坡体积15 000 m3),雨停后，Fs值逐渐回升。图9(b)为Fs值随关键岩土参数c′，φ′和ks的变化情况。在后验分布μc′±2.0×νc′(均值加减两倍标准差)范围内将给Fs带来18%的变化，μφ′±2.0×νφ′将导致高达72%的Fs变化，ks也有不可忽视的影响，μks±2.0×νks会导致10%的Fs变化。上述结果表明，曾经失稳的老滑坡安全系数Fs值往往集中在1.1～1.5之间，接近于1.0的临界值。因此，研究Fs的不确定性具有重要的实用价值。如图9(c)所示，随机变量的可靠指标βRV与相关系数呈线性负相关关系，τc′,φ′和τks,φ′对可靠指标影响较大。可靠指标βRV=0.622，对应的失效概率为26.6%。综上所述，若采用随机变量的可靠指标，则需要采取减小坡角、施加抗滑桩、开挖排水沟等措施，以防止发生新的滑坡灾害。

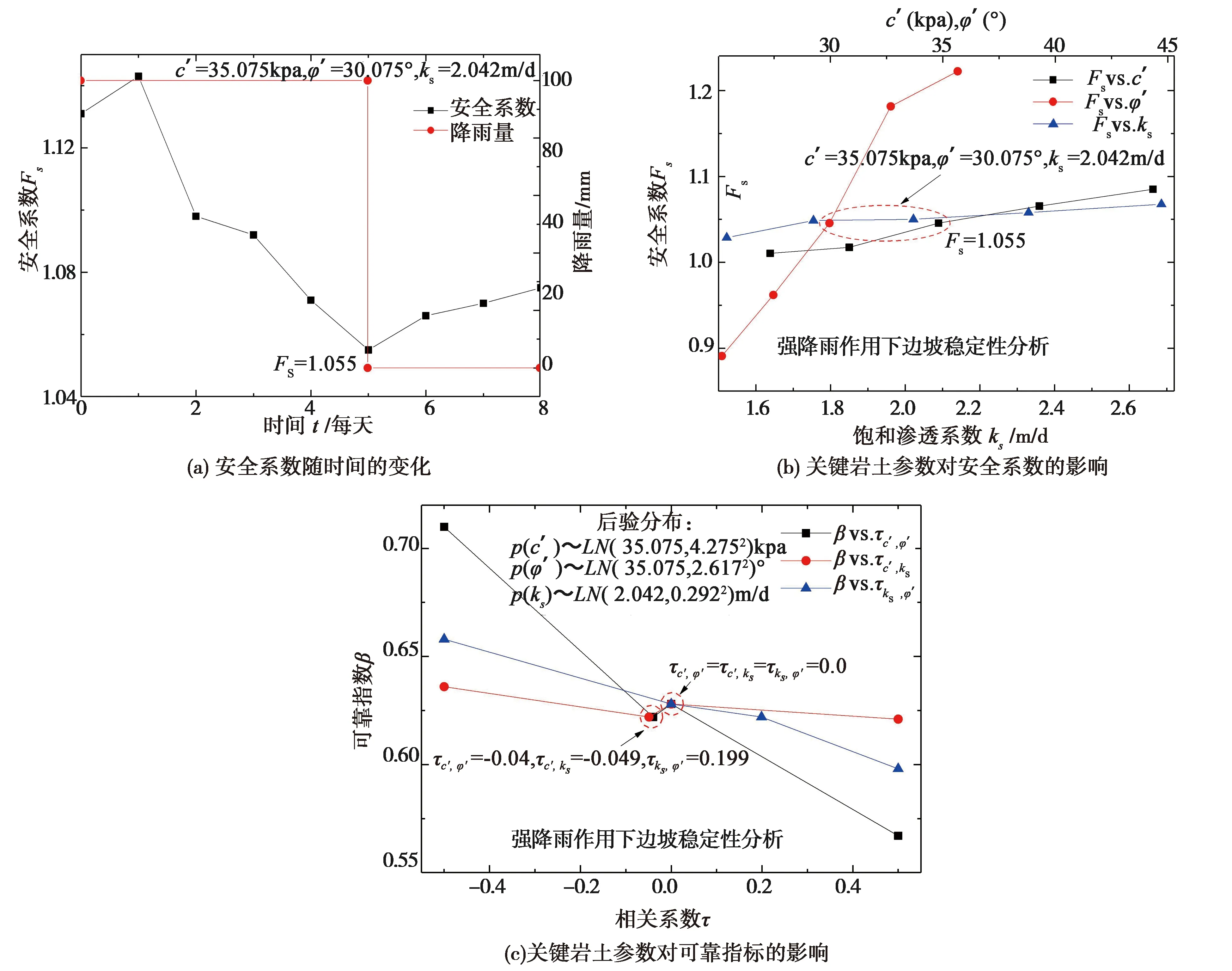
图9 采用随机变量法分析石榴树包边坡稳定性Fig.9 Stability analysis of Shiliushubao slope with random variable method

(2)随机场变量的可靠度分析

随机场变量的可靠度分析考虑了关键岩土参数的空间变异性，从而获得更精确的结果。其中使用SMC算法计算可靠指标，需要2个参数：子集抽样N和失效比率p0。N从100变化到1 500，p0分别取0.05、0.10和0.15。因此，如图10所示，随机场变量的可靠指标变化分为2个区域，左侧为不稳定组合，右侧是稳定组合，为了平衡精度和效率，N=1 000是最佳选择。在p0=0.10时可靠指标βSRF达到最大βSRF=2.470，相应的失效概率Pf为0.7%。与经典的MC算法相比，SMC算法仅进行3 000次随机计算，减少了1/3的运行时间，提高了计算效率。

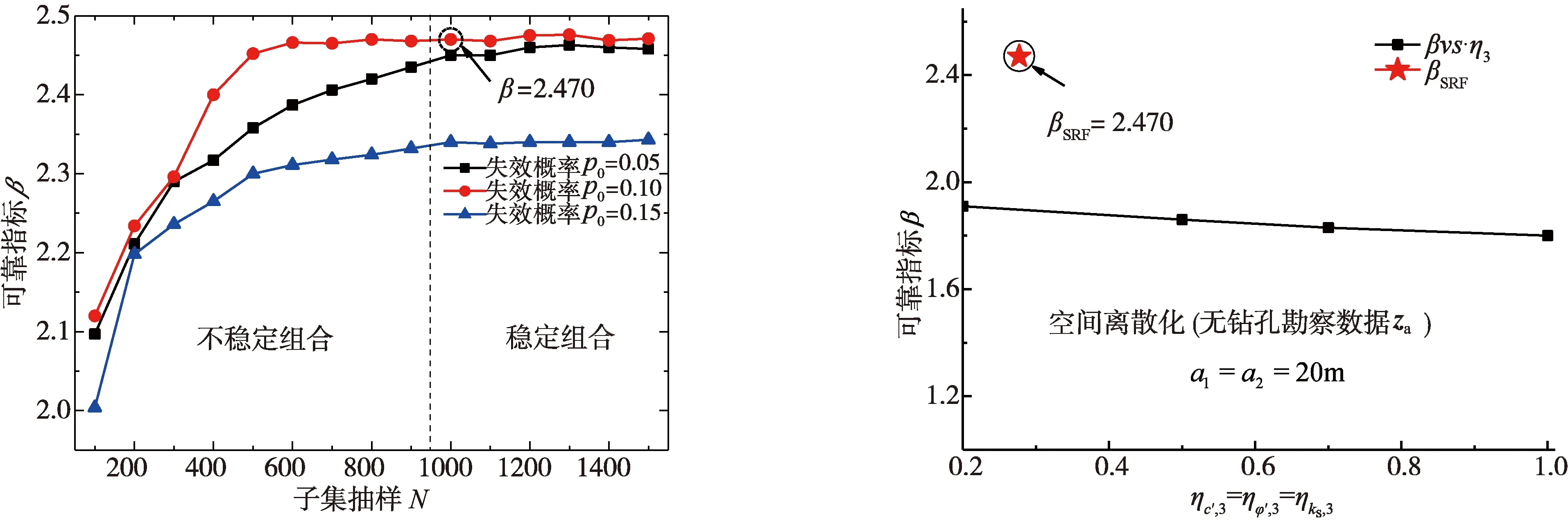
图10 SMC算法计算边坡稳定性可靠指标 图11 可靠指标与第三变程比率η3的关系Fig.10 Reliability index of the slope stability per SMC algorithm Fig.11 Relationship between reliability index and the third range ratio

图11讨论了在无钻孔勘察数据za的情况下，随机场变量的可靠指标β与第三变程比率η3的变化情况。随着变程比率η2的增大，可靠指标β逐渐减小。当随机场变程a1=20 m，ηc′,3=ηφ′,3=ηks,3=0.2时，βSRF=1.91，表示各向异性随机场的结果。当随机场变程a1=100m，ηc′,3=ηφ′,3=ηks,3=1.0时，βSRF=1.44，表示各向同性随机场的结果。当变程不断增大，可靠指标βSRF逐渐趋近于相应的随机变量可靠指标βRV=0.622。以上研究意味着如果随机场的变程足够大，随机变量是随机场变量的一个特例。在实际工程应用中，将岩土参数视为随机变量提供了较为保守的预测，而随机场变量提供了更为准确的预测结果。值得说明的是可靠指标βSRF远大于βRV值，随机场理论主要考虑了钻孔勘察数据和关键岩土参数的空间变异性，这也在一定程度上解释了为什么边坡的安全系数比较小，但仍然保持稳定的原因。

4 结论

本文基于考虑渗流的非饱和土边坡稳定分析理论，采用随机场-贝叶斯方法校准了关键岩土参数，并以三峡库区石榴树包滑坡为例进行边坡稳定性的可靠度分析，得到以下结论：

(1)根据钻孔勘察数据、2012年度库区水位变化和降雨量、以及边坡表面沉降数据，分季度对关键岩土参数进行校准，得到的后验均值均小于钻孔勘察数据统计值，说明直接采用原始钻孔勘察数据进行边坡稳定性分析将有风险。

(2)在夏季三峡库区水位152 m，连续5天降雨量为100 mm的假定情况下，将校准后的岩土参数视为随机变量，计算得到的可靠指标为0.622，对应的失效概率为26.6%。岩土参数对安全系数的影响从大到小依次为有效内摩擦角、有效凝聚力和饱和渗透系数。

(3)在实际工程应用中，随机场方法考虑了钻孔勘察数据和关键岩土参数的空间变异性，为边坡稳定性可靠指标提供了更为准确的预测结果。将校准后的岩土参数空间统计特征代入夏天枯水位强降雨条件下进行边坡稳定性分析，结论是无需采取额外的加固措施来防止发生新的地质灾害，但建议监测系统应继续提供长期监测数据。