基于分形理论与SVM的河冰高分遥感影像智能识别方法研究
苑希民,韩 超,徐浩田,田福昌
(天津大学水利工程仿真与安全国家重点实验室,天津 300350)
凌汛灾害是黄河影响最为严重的自然灾害之一,其影响因素众多,成灾机理复杂,并具有突发性和持续性,为黄河凌汛防御工作带来诸多挑战,素有“伏汛好抢,凌汛难防”之说[1]。凌汛灾害一旦发生,将对沿岸农业生产、基础设施以及人民生命财产带来严重影响[2]。近年气候变化影响下,黄河凌汛灾害发生频率呈现升高趋势,尤其是内蒙古河段,特殊的地理位置、气候条件及河道走向使其成为黄河凌汛灾害最为严重的河段之一[3],1987~2018年间发生不同程度的凌汛灾害百余次,由平均1.6年/次上升到0.3年/次[4],这对我国凌汛灾害防御工作提出了更高要求。
众多学者针对凌汛灾害开展了大量研究,苑希民等[5]采用基于遗传算法的神经网络方法建立了凌情智能耦合预报模型,对流凌、封河、开河日期进行了预报;刘吉峰等[6]分析了黄河宁蒙河段冰凌2000年以来的变化特点;顾润源等[7]研究了气候变化对黄河内蒙古段凌汛期的影响。目前在凌汛研究中,数据分析和数值模拟等主要手段对观测数据的需求量较大,传统野外观测得到的数据在尺度等方面具有局限性,已在水利领域得到广泛应用的遥感技术具有宏观性能高、更新周期短、抗人为干扰因素强等优点[8-9],可有效地弥补传统观测方法的不足[10]。
当前遥感监测冰情的技术,大多应用在海洋和湖泊等较为宽阔的水域,主要用于监测海冰面积和边缘[11]、冰湖数量[12]、冰湖面积[13]等,相比而言,由于大多数河流有限的宽度,河冰的研究较为局限,大多是针对低分辨率大范围影像,Naira等[14]提出了一种基于阈值的决策树图像分类算法来处理MODIS数据并确定河冰范围的方法;H B Wang等[15]提出了一种基于无人机遥测技术的黄河冰柱定位监测的视频数据处理方法;Kraatz等[16]提出了一个可供选择的MODIS河冰监测算法,它可以在无云条件下和通过一些半透明的云识别河冰;Beaton等[17]开发了一种利用MODIS图像自动检测驼鹿河等五条河流开河的方法。
以往研究均为对大幅影像的解译[18],缺少对河冰细部特征的识别分析以及河冰遥感影像的精细化分类,这也正是本文的先进性所在。
本文针对凌汛灾害频发的黄河内蒙古段,选取典型河段为研究区域对象,对黄河内蒙古包头段黄牛营子村处弯道的河冰进行分形智能分类识别研究。
1 数据及原理
1.1 技术路线
本文技术路线如图1所示,具体为:均匀分块裁剪研究区域的河冰高分遥感影像,在经过灰度化和滤波去噪等预处理措施之后,进行分形特征边缘检测,基于该检测结果和对遥感影像的目视解译选择分类的分类样本,通过支持向量机算法进行智能分类,基于混淆矩阵计算分类精度并对比分析分类结果与分形结果。
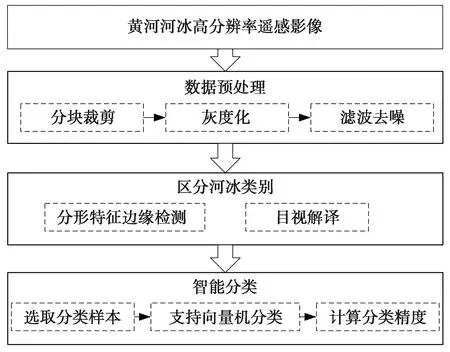
图1 技术路线图Fig.1 Technology roadmap
1.2 影像预处理
对获取的遥感影像进行预处理,包括分块裁剪,灰度化和滤波去噪。将遥感影像均匀分块,保证每一图块仅包含一种河冰类型,便于后续处理区分。
为获得清晰的、高质量的遥感图像,本次研究中采用中值滤波进行降噪预处理。中值滤波是当前应用最广泛的去噪方法之一,它在一定的条件下可以克服线性滤波、均值滤波等带来的图像细节模糊,而且对滤除脉冲干扰及图像扫描噪声最为有效[19]。
中值滤波器一般采用一个含有若干个点的滑动窗口,将窗口中几个点灰度值的中值来替代指定点(窗口的中心点)的灰度值。大多选取二维窗口,窗口的尺寸逐渐增大,直到滤波效果满意为止。
图2为河冰原始影像图块及其灰度图块,对其进行模板为7×7,9×9和11×11的中值滤波后的灰度图像及二值化后的图像。从图中可以看出,采用7×7的模板对原图像进行中值滤波后,去除了部分噪声,但图像中噪声还是很明显;采用11×11模板的中值滤波虽然噪声滤除噪声能力加强,但是图像出现模糊和断续现象;采用9×9模板滤波后噪声得到了很好的抑制,同时图像特征得到了很好的保存,因此最终采用9×9中值滤波模板。

图2 河冰影像及其灰度化和二值图像Fig.2 River ice image and its grayscale and binary image
中值滤波有三方面优点:1)降低噪声能力较强;2)在灰度值变化较小的情况下可以得到很好的平滑效果;3)不会使图像的边界部分过分模糊。
1.3 河冰影像的分形特征边缘检测
图像中不规则的对象无法用传统的欧几里德几何学来描述[20]。Benoit B. Mandelbrot于1975年创立了分形几何学,用分形(Fractal)一词来表述那些没有特征长度,具有无限精细结构的图形、构造及现象[21]。分形几何图形具有自相似性和递归性,易于计算机迭代,擅长描述自然界存在的景物[22-23]。
在实际应用中,常用Richardson定律来计算分形维数[24]。
M(ε)=Kεd-D.
(1)
式中ε=1,2,3……为尺度因子,M(ε)约是尺度ε下的度量特征值,D是分形维数,d是拓扑维数,K是分形系数。对于二维灰度图像,M(ε)约取为图像表面积测度A(ε),则有
A(ε)=Kε2-D.
(2)
一幅图像可以看成高度正比于其灰度值的山丘,这个曲面的上下ε构成厚度为2ε的“毯子”。对于不同的ε,“毯子”的面积即图像的表面积A(ε)可以由“毯子”的体积除以2ε得到。
设f(i,j)代表图像的灰度值,U(i,j,ε),B(i,j,ε)分别表示上表面和下表面的灰度值,令
U(i,j,0)=B(i,j,0)=f(i,j).
(3)
上下两张“毯子”分别以如下方法变化:
U(i,j,ε+1)=max {U(i,j,ε)+1,maxm,n∈η[U(m,n,ε)]}.
(4)
B(i,j,ε+1)=min{B(i,j,ε)-1,minm,n∈η[B(m,n,ε)]}.
(5)
式中η={(m,n)|d[(m,n),(i,j)]≤1},d(•)表示两点之间的距离。
于是“毯子”的体积为V(i,j,ε)=∑(i,j)∈R(U(i,j,ε)-B(i,j,ε)) ,R表示图像上以(i,j)为中心的取值区域,故表面积A(i,j,ε)=V(i,j,ε)/2ε。
计算不同尺度下的A(i,j,ε),由式logA(ε)=(2-D)logε+logK可知利用点对 [logA(i,j,ε),logε],采用线性最小二乘拟合的方法,由拟合直线的斜率即可求出分形维数D。
黄河河冰的形状是自然产生的,同一种河冰范围内的形状具有一定的自相似性,因此可以利用其分形特征,来实现对河冰影像的分割,从而更加清晰地区分不同种类的河冰。
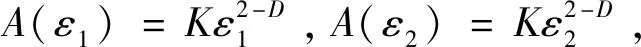
(6)
K反映了图像灰度表面积随尺度变化的空间变化率。对式(2)两端取对数,得
logA(ε)=(2-D)logε+logK.
(7)
上式表示在logA(ε)-logε坐标下的一条直线,logK为该直线在纵坐标轴logA(ε)上的截距,K相当于该尺度下的灰度曲面面积。当光滑的曲面或灰度变化缓慢的灰度曲面,K值较小;而当起伏较大的灰度曲面或灰度变化较为剧烈的曲面,K值较大。不同纹理灰度表面之间,灰度起伏变化相对无论哪一种纹理图像来说都更加显著,因此K值也能够反映图形灰度表面的粗糙程度。大多数纹理图像可以用分形模型进行描述[25],河冰影像即由不同纹理区域组成,在不同纹理灰度表面之间(即图像的边缘处),灰度变化比较大,即K值较大。所以我们可以用K值作为分形特征,对河冰影像进行分割。算法如下:
(1)以M×M的窗口作为局部处理区域,从河冰影像的起始点开始,从左到右,从上到下,按照ε-毯子法依次计算每个窗口中心像素的分形特征K,从而将河冰影像的灰度空间映射为分形特征K空间;
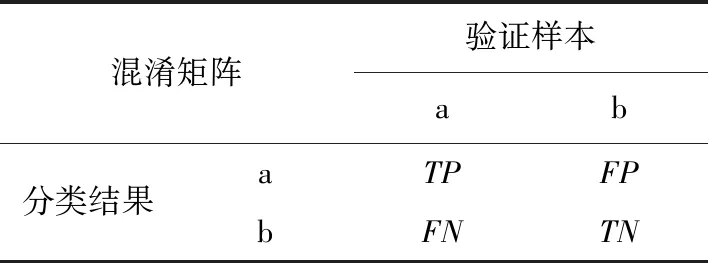
(2)采用自适应门限对K空间进行二值化。找出K空间的最大值Kmax,并选取适当的系数a (0 支持向量机(SVM)是一种基于统计学习理论的模式识别算法,能够根据有限的样本信息寻找最优分类结果。SVM非线性分类的思想是把输入样本经过非线性变换映射到高维核空间,在高维核空间中寻找最优分类超平面,将样本集分为两类,并使两类间隔最大[26]。 设有一个最优超平面[27]能将两个类别分开,可用下式(8)表示: f(x)=wTφ(x)+b. (8) 其中w、b分别为超平面的法向量和截距,φ(x)表示将x映射到更高维空间后的特征向量。 为使间隔最大化,有 (9) (10) 利用核函数K(xi,yi)进行求解,如下 K(xi,xj)=<Φ(xi),Φ(xj)>=Φ(xi)TΦ(xj). (11) 即可得到, (12) 其中αi指样本。 SVM中有3种非线性核函数:多项式核函数、径向基核函数和Sigmoid核函数。本研究选择径向基核函数作为分类函数。与其他核函数相比,径向基核函数的参数更少,且性能稳定[28]。 本研究选择SVM基于以下几点考虑: (1)SVM是基于小样本统计理论的学习方法,可以较为快速地处理较大数量的训练样本[29]; (2)SVM利用核函数将本研究中低维线性不可分问题转化为高维线性可分问题,同时利用核函数简化了高维空间问题的求解难度,提高了分类效率; (3)SVM是基于结构风险最优化原则,与其他传统学习方式相比,避免了过学习问题,泛化推广能力强[30]。 在分类型模型评判的指标中,常见的方法有如下3种,分别是混淆矩阵、ROC曲线、AUC面积。本研究选用混淆矩阵进行分类后的评价。混淆矩阵就是分别统计分类模型归错类,归对类的观测值个数,然后把结果放在如表1中展示出来。 表1 混淆矩阵精度报表Table 1 Confusion matrix accuracy report 验证样本(即真实值)是a,模型认为是a的数量为TP,验证样本是a,模型认为是b的数量为FN; 验证样本是b,模型认为是a的数量为FP,验证样本是b,模型认为是b的数量为TN。 将这4个指标一起呈现在表格中,就能得到混淆矩阵。 主要的评价指标为准确率ACC和Kappa系数,ACC代表分类模型所有判断正确的结果占总观测值的比重[31],其计算如下式 (13) Kappa系数是主要用于一致性检验的分类精度指标,起计算如下式 (14) 黄河内蒙古段位于黄河干流最北端,纬度较高,相比黄河上游兰州段北进约4.5°,从伊克昭盟的拉僧庙进入内蒙古境内,至榆树湾出境,全长840 km,而总落差仅162.5 m[32],研究区域图如图3所示。内蒙古的冬天严寒而漫长,黄河流经之处的冬季平均气温较上游骤降4~6℃[33]。由于气温的大幅降低以及河道比降小等因素,黄河内蒙古段下游先封河,上游先开河,流凌封冻通常早兰州20余天,而解冻开河要晚一个多月。同时该河段弯道和河面束窄遍布,极易发生卡冰结坝[34],尤其是在每年的开河期,大量冰水混合下泄,会形成极大的凌峰,使得黄河内蒙古段凌汛灾害频发且严重,据1951~2011年宁蒙河段各断面凌情及凌灾统计,平均每年发生冰情5.77次,每两年就会发生一次较严重的凌灾[35],这对两岸人民群众的生命财产安全形成了巨大的威胁。 图3 研究区域图Fig.3 Study area map 此次实验区域如图4所示,位于黄河内蒙古包头段黄牛营子村处弯道,所选区域尺寸为3 000 m×3 000 m。影像区域内河冰种类丰富,包括冰塞(下面带有冰礁的冰盖),透明冰,清沟以及平滑冰盖,实验中按照这四类冰对影像进行分类。 图4 实验区域Fig.4 Experimental area 本研究采用的是Worldview-3遥感数据,成像时间为2018年2月24日,分辨率0.31m每像素,包括红绿蓝3个波段。研究区域影像有以下特点: (1)清沟颜色呈黑色,透明冰呈深蓝色,目视解译较为清楚明了; (2)清沟上下游有冰盖及冰礁等河冰,均呈白色,冰礁在影像的表现形式上表现为圆状斑点; (3)由于较薄的平滑冰盖与遍布冰礁的冰塞颜色相仿,不容易区分,但是后者较前者导致凌汛的风险大大增加,因此需要进一步的处理对二者进行细致的区分。 基于以上这些图像特征,传统的单一的算法很难实现准确的区分和识别,因此融合多种处理技术,采用有针对性的处理方法是很有必要的。 将区域图均匀分割成900个100 m×100 m的图块,剔除实验区域中的裸地、森林等与河冰无关的图块,保留涉及到河冰的图块,如图5所示。 图5 均匀分割后图块Fig.5 Evenly segmented graph block 保证每一个图块仅包含一种河冰的种类,这样在分形程序处理之后,通过得到的不同处理结果能够有效地区分河冰的种类。 对图块进行灰度化,避免影像失真,易于后续处理。 滤波去噪。使用中值滤波方法进行去噪,经调试比较,采用9×9模板的中值滤波去噪能力最强,同时也能够较好地保留河冰的特征。 采用上述基于河冰分形特征的影像边缘检测与分割的方法进行实验,选择2×2窗口作为局部处理区域,系数a取0.8,选取尺度为2<ε<8。 通常认为,黄河河曲段所结冰盖是由岸冰、流凌冰块、水内冰花结合生成[36]。在水流有湍急流动的区域,水体产生大量的水内冰,水内冰向下游流动、积聚,与流凌冰块或岸冰粘结附着,另外黄河泥沙含量高,在结冰的过程中,还会出现异类成核的现象,即水中围绕上游下泄冰块以及水体中的杂质首先结冰,在冰盖形成时后也处于冰盖中冰厚最大的位置,极易形成冰礁和锚冰等阻水,增加凌汛风险。 从实验结果看,边缘检测能够很好地识别到冰礁,如图6(a)中的冰礁位置,分形处理后如图6(b)所示,每一处冰礁被识别成团状,1986年在国际冰凌学术会议上曾给冰塞定义为:阻碍水流的碎冰或冰花的固定集合体。从这个意义上来说,大的锚冰或阻水的冰礁都属于冰塞,只是规模大小和部位不同。因此本研究将识别出冰礁的冰盖统一归类为冰塞。 图6 冰塞影像及其分形处理结果Fig.6 Ice jam image and its fractal processing results 而对于厚度较薄的平滑冰盖来说,通常是由两岸岸冰向河心延伸而成,另外清沟的出现减少了向下游输送的流冰,使得清沟下游的冰盖厚度较薄,表面平滑,分形纹理不够明显,因此分形程序无法检测到边缘,其处理结果的像素灰度值全部为0,表现为黑色。 通过不同的分形结果,可以有效地区分冰塞和平滑冰盖,全部图块识别结果如图7所示。从分形结果图中可以看出,首先对于清沟的识别十分准确,可以看出分形识别的清沟轮廓与原图相符;另外冰塞主要分布在图中红框的位置,而平滑冰盖主要分布于图中黄框位置。 图7 图块分形结果图Fig.7 Graph block fractal result graph 分析清沟产生的原因,首先,上游弯道处形成冰塞卡冰,使下游的来冰量减少,无法形成冰盖;其次,整个弯道呈几乎180°拐弯,流凌和冰块在离心力的作用下堆积在下游弯道的外侧,使弯道内侧形成清沟。该影像时间为二月末,黄河沿岸气温有所回升,此时清沟的出现和扩大也预示着开河的临近,有关部门应该加强警惕,谨防开河期凌汛灾害的发生。 对2017年11月27日(距所研究高分影像的时间最近)的遥感影像进行水体识别,获得了较为精确的水体范围,由于黄河内蒙古段支流流入补给的流量较少,冬季水位变化小[37],因此可以认为该水体范围与河冰范围相差无几,可以用水体范围图层对研究区域进行裁剪,剔除非河冰部分的像素,减少其他地物对河冰识别精度的干扰,裁剪之后影像如图8所示。 图8 裁剪后的实验区域 图9 分类样本选取图 图10 支持向量机分类结果图Fig.8 Trimmed experimental area Fig.9 Classification sample selection diagram Fig.10 SVM classification results 根据分形特征边缘检测结果得到的河冰类别,结合目视解译,对原始影像进行分类样本的选取。将影像中河段分为前两公里和后一公里两段,在前两公里河段进行分类样本的选取,后一公里河段用于验证。共选取4种分类样本,共246个,如图9所示(其中红色是冰塞63个,绿色是平滑冰盖39个,蓝色是透明冰59个,黄色是清沟85个)。 本研究实现SVM多分类的方法分两步,第一步是依次把某个类别的样本归为一类,其他剩余的样本归为另一类,根据4个类别样本构造出4个SVM分类器,如下: (1)冰塞为一类,平滑冰盖、透明冰、清沟为另一类; (2)平滑冰盖为一类,冰塞、透明冰、清沟为另一类; (3)透明冰为一类,平滑冰盖、冰塞、清沟为另一类; (4)清沟为一类,冰塞、透明冰、平滑冰盖为另一类。 第二步是将上述4种分类结果进行测试,每个测试都有一个结果f1(x),f2(x),f3(x),f4(x),分类时将未知样本分类为具有最大分类函数值的那类,于是最终的结果便是这4个值中最大的一个作为分类结果。利用支持向量机进行分类,分类结果如图10所示。 基于混淆矩阵对遥感影像的分类精度进行评价,通过对研究区域的目视解译结果随机取样,在后一公里河段随机生成 125个样本作为精度验证样本分类结果的混淆矩阵如表2所示。 表2 分类结果混淆矩阵Table 2 Confusion matrix of classification results % 从表1可得,与验证样本对比,该方法将94.21%的平滑冰盖像元正确分类为平滑冰盖,5.76%的平滑冰盖像元分类为冰塞,0.03%的平滑冰盖像元无法分类,分类为其他类别;将96.68%的清沟像元正确分类为清沟,3.32%的清沟像元无法分类,分类为其他类别;将97.71%的透明冰像元正确分类为透明冰,2.24%的透明冰像元分类为冰塞,0.05%的透明冰像元无法分类,分类为其他类别;将79.87%的冰塞像元正确分类为冰塞,18.69%的冰塞像元分类为平滑冰盖,1.43%的冰塞像元分类为透明冰,0.01%的冰塞像元无法分类,分类为其他类别。即本方法准确预测分类了94.21%的平滑冰盖像素,96.68%的清沟像素,97.71%的透明冰像素以及79.87%的冰塞像素,根据式(13)计算准确率达93.05%,即研究区域影像中共有93.05%的像素被准确分类。另外Kappa系数达 0.9026,说明本分类方法在考虑错分漏分情况下依然表现出较好的分类效果,说明本分类方法较为准确可信。 针对黄河河冰高分遥感影像的几何特征、空间特征和纹理特征等复杂信息,本文选取黄河内蒙古段为研究对象,提出一种高分遥感影像凌汛灾害信息识别提取方法,开展河冰影像精细化分类与智能识别研究,具体研究结论如下: (1)对河冰的高分遥感影像进行分形特征边缘检测,精细化提取河冰信息,将河冰影像分为冰塞、透明冰、清沟及平滑冰盖四类,准确地识别出河冰的种类及不同类别所在的位置; (2)基于河冰分形特征的边缘检测结果选取河段分类样本,利用支持向量机进行智能分类识别,总体分类结果达到93.05%,智能方法分类结果精度较高,且与分形特征边缘检测的结果一致,本研究方法相对准确可靠; (3)随着高分遥感影像的飞速发展,通过对河冰影像智能分类分析研究,可对凌汛灾害进行有效的识别及信息提取,可为凌汛灾害风险的预测评价提供理论方法支撑,对提升凌汛灾害的综合防控能力具有重要意义。1.4 河冰影像的智能分类及评价
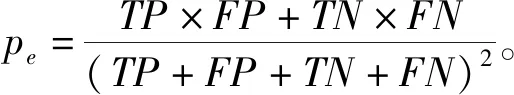
2 河冰高精度分类识别过程与结果分析
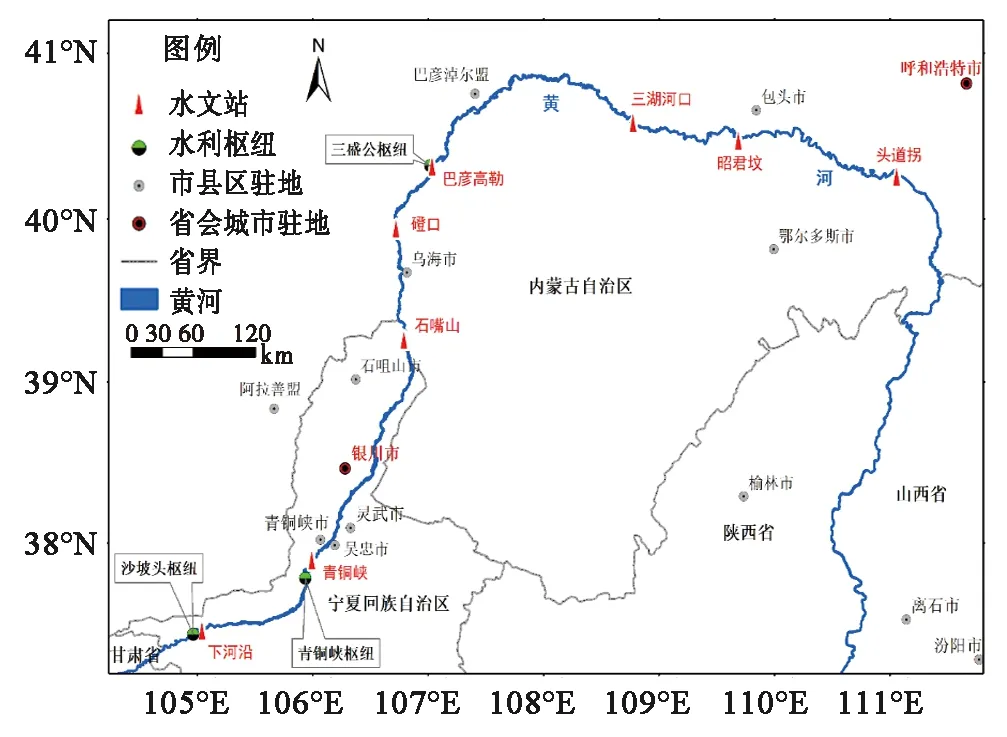
2.1 研究区域及实验区域概况

2.2 数据介绍
2.3 影像的预处理

2.4 河冰影像的分形特征边缘检测实验


2.5 河冰影像智能分类

2.6 分类结果评价
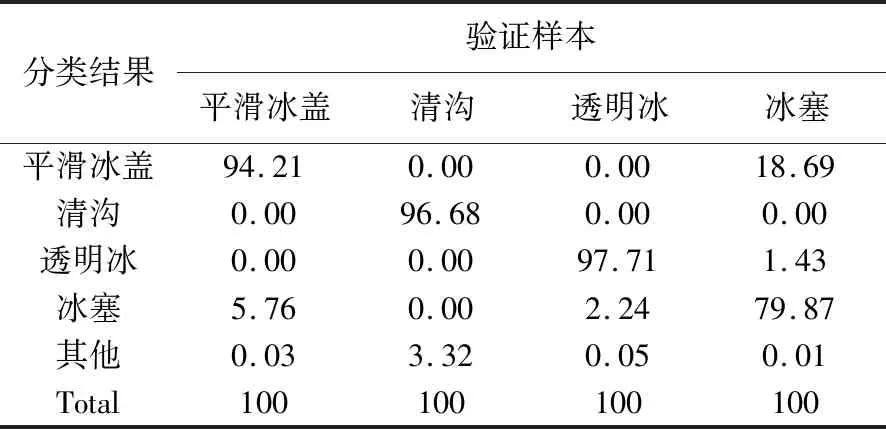
3 结语

