城乡居民基本养老保险参保人数预测

许 燕

（福建江夏学院金融学院，福州350108）

一、引言

2014年新农保和城居保从制度上的整合①2009年9月1日颁布了《关于新型农村社会养老保险试点的指导意见》（国发〔2009〕32号），开展新型农村社会养老保险（简称新农保）试点。2011年6月7日，国务院又发布了《关于开展城镇居民社会养老保险试点的指导意见》（国发〔2011〕18号），（简称城居保）。，统一了城乡居民基本养老保险制度，使得我国养老保险实现了制度上的广覆盖，这对于促进我国国民经济持续、快速、健康、稳定地发展发挥了重要作用。在城乡居民养老保险制度下，2014～2017年，政府补贴额由1644亿元增长到2494亿元，个人缴费额由666亿元增长到810亿元，基金支出从1571亿元增长到2372亿元。显然，政府补贴额度呈现出快速增长的趋势，而个人缴费增长速度要低于基金支出增长速度。另据统计数据表明，全国65岁及以上的老年人口占全国人口的比重由2000年的7%上升到2017年的11.4%②数据源于2018《中国统计年鉴》。，远超了联合国规定的7%的红线。这种未富先老的人口结构不仅影响到经济的可持续发展，更是增加了养老保险基金支付的压力。人口老龄化、高龄化的趋势必然导致年领取城乡居民养老保险金人数的增多，对政府财政支出形成一定压力，并将影响到52392万③《2018年度人力资源和社会保障事业发展统计公报》显示：城乡居保参保人数52392万人，其中，领取待遇人数为15898万人。城乡居民的福祉和社会稳定。因此，对城乡居民参保人口数据进行预测是开展城乡居民基本养老保险基金收支平衡测度及养老保险制度财务可持续性研究的重要基础。

二、城乡居民基本养老保险制度概述

据国发〔2014〕8号文件，城乡居民基本养老保险实行的是社会统筹与个人账户相结合的制度模式。社会统筹账户的基金来源于中央政府补贴和地方政府提高和加发的基础养老金，用来支付符合条件的满60岁及以上的城乡居民的基础养老金。个人账户的基金主要来源于个人缴费及地方政府对个人缴费的补贴。除此之外，集体补助及其他社会经济组织、公益慈善组织、个人对参保人的缴费资助也都记入参保人的个人账户。关于城乡居民养老金收支理论分析框架如图1所示。

从图1人口预测部分可以看出参加城乡居民基本养老保险的人群主要包括16～59岁的缴费人群和60岁及以上的领取待遇人群。而60岁及以上的领取待遇人群又可分为有个人账户的城乡居民和没有个人账户的城乡居民。显然，城乡居民养老保险基金不仅要不断接收参保居民缴费，还要在长期内负担领取待遇人群未来应得的养老金，而参保居民的人数及参保人的年龄分布将会对城乡居民基本养老保险制度财务可持续性产生极其重要的影响。

图1 城乡居民基本养老保险基金收支理论分析框架

三、城乡居保参保人口预测

影响城乡居保参保人口的因素主要体现在死亡率、生育率、参保率和迁移率上。由于本文的研究对象为城乡居民参保人口，国内人口无论是在区域间流动还是在城乡之间流动，并不会对城乡居民参保人数的规模产生影响，而人口的国际间迁移对城乡居民参保人数的影响基本可忽略不计。因此，在做城乡居民参保人数预测时我们主要分析死亡率和生育率的随机性变动及参保率对城乡参保居民人口规模的影响，从而不考虑迁移率。因此，我们将利用随机模型，根据统计数据，预测未来分年龄性别死亡率和分年龄生育率，运用分要素推移法预测未来城乡居民人口。在利用统计数据求得分年龄段总参保率的基础上，结合现实情况利用规划求解得到城乡居保分年龄参保率，从而进一步分析城乡居保分年龄参保人数，并为城乡居保基金收支测算提供科学依据。

（一）城乡居保参保人口预测模型及方法

1.全国分年龄性别人口预测模型及方法

由于新出生人口数主要和育龄妇女人数及其生育率有关，而0岁以上人口数主要和死亡率有关，因此，二者的预测模型并不相同，以下将分别介绍。

如果假设δ为出生性别比，将式（1）中0岁人口数乘以δ，则可预测该年全国0岁年龄性别人口数。一般情况下，设定男婴占比为0.515，女婴占比为0.485①参见李永胜.人口预测中的模型选择与参数认定.财经科学，2004（2）：69。此外，2010年第六次人口普查数据显示，0岁男婴占比约为0.5412，0岁女婴占比为0.4588。。

0岁以上各年龄性别人数估计可根据全国分年龄性别实际人口基数和所预测的死亡率，采用分要素推移法即人口平衡方程来预测，其中人口平衡方程表达式为：

由式（1）和式（2）可对全国分年龄性别人口进行预测。

2.城乡居保参保人数测算方法

按国发〔2014〕8号文件规定，年满16周岁（不含在校学生），非国家机关和事业单位工作人员及不属于职工基本养老保险制度覆盖范围的城乡居民，可以在户籍地参加城乡居民养老保险。因此，根据文件规定，首先，需要求出符合城乡居保参保条件的16～59岁人口。而符合城乡居保参保条件的16～59岁人数等于全国16～59岁人数减去在校学生数、机关事业单位16～59岁人员数和企业职工基本养老保险16～59岁参保人数。其次，需求出符合城乡居保参保条件的60岁及以上人口。符合城乡居保参保条件的60岁及以上人数等于全国60岁及以上人数减去机关事业单位60岁及以上人数和企业职工基本养老保险60岁及以上人数。最后，将符合城乡居保参保条件的分年龄人口数乘以对应的城乡居保分年龄参保率即可获得城乡居保分年龄参保人口。（所有16岁以上全国人口、在校生、机关事业单位人员、企业职工均分性别按上述计算方法来求，最后再将计算所得的同一年龄的符合城乡居保参保条件的男性、女性人数求和。）

（二）城乡居保人口参数预测模型与方法

1.死亡率预测模型及方法

Lee和Carter（1992）[1]提出的Lee-Carter模型（简称LC模型）属于经典的离散型随机死亡率模型，模型的构建主要对对数中心死亡率数据进行统计分析，在此基础上考虑死亡率的随机性变动因素。模型的具体表达式如下：

其中，mx,t为中心死亡率，αx表示年龄x岁的死亡率对数的平均值，βx为年龄x岁对死亡率变动的敏感度，κt为和时间相关的参数，反映死亡率随时间t变化程度；ξx,t为误差项，其均值为0且方差为

该模型非常简洁，三个参数αx、βx和κt意义也很明确，在预测死亡率方面得到了极广的应用。但是，针对本文的研究，LC模型在实际应用时，需解决以下三个方面问题：一是关于参数估计方法选取的问题；二是经典的LC模型在中长期预测中存在性别差异扩大问题；三是对高龄人口死亡率预测时缺乏统计数据问题。

关于LC模型参数估计方法有很多。最初的LC模型参数是用矩阵奇异值分解（Singular Value Decomposition，简称SVD）的方法来估计的，但是Lee和Miller（2001）[2]及Brouhns（2002）[3]指出SVD方法暗含不同年龄死亡率的误差具有相同的方差。Wilmoth（1993）[4]提出以死亡人数的倒数为权重，采用加权最小二乘法来估计LC模型参数，但当统计数据中死亡人数有缺失时，加权最小二乘法将无法使用。Brouhns等人（2002）[3]改进了SVD方法估计中不同年龄死亡率的误差具有同方差的假设，提出用极大似然估计法（MLE）来估计LC模型参数。假定死亡人数dx,t服从参数为λx,t=Ex,t·eα^x+β^xκ^t的泊松分布（Ex,t为t年x岁死亡风险暴露人数），经推导，总体对数似然函数表达式如下：

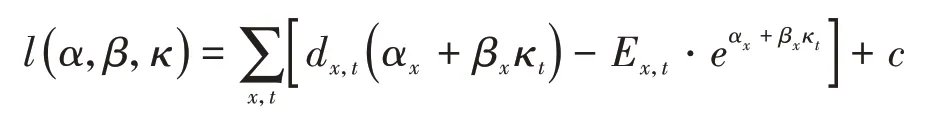
其中c为与λx,t无关的一个常数。

当似然函数达到极大时，应可以求出模型参数的极大似然估计值。但似然函数式子中存在二次项βxκt较难求解。Brouhns等人（2002）[3]利用Goodman（1979）[5]提出的迭代方法，就是每个参数在ν+1次迭代时，其他参数的ν+1次值保持ν次值不变，三个参数按如下迭代公式进行迭代：

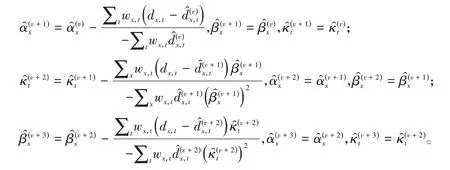
其中，wx,t为权重，当数据存在时权重为1，数据缺失时权重为0。在迭代时，需要设定αx、βx和κt估计值的初始值（不唯一），一般可令=0。在第ν次迭代时，应满足的条件。迭代进行到对数似然函数前后两次估计值的偏差足够小（比如偏差绝对值小于10-10）时停止。另外，从模型可以看出，在保持经典的LC模型不变的条件下，模型中的三个待估参数可以通过任意常数来进行转换，因此，要对迭代后的βx和κt增加约束条件，即从而保证估计值的唯一性。

Li和Lee（2005）[6]在研究时发现经典的LC模型在预测时分男女进行，得到男性和女性的三个参数αx、βx和κt值也不同，在中长期预测中，男女死亡率随着时间的推移差异变大。针对这一问题，有学者（黄匡时，2015[7]）提出采用LC模型的相干模型①黄匡时运用中国人口死亡率数据，采用Lee-Carter模型的相干模型来解决死亡率预测中性别差异扩大的问题。来进行改进。所谓LC模型的相干模型，其实质就是在死亡率预测时采用三组数据估计参数，一是采用混合人口死亡率历史数据（不分性别）得到一组αx、βx和κt估计值，二是采用男性死亡率历史数据得到另一组αx、βx和κt估计值，三是采用女性死亡率历史数据得到再一组αx、βx和κt估计值。在分男女对人口的死亡率进行外推时，参数αx估计值采用的是分性别的估计值，而参数βx和κt采用的混合人口数据（不分性别）估计值，以此来解决中长期预测中男女死亡率差异扩大问题。

在高龄人口死亡率预测中，Cairns-Blake-Dowd（2006b）[8]提出两因素随机死亡率模型（简称CBD模型）预测高龄人口死亡率。模型的具体表达式如下：

其中，logitq(x,t)=式中q(t,x)为t年x岁的人的条件死亡概率，与中心死亡率的关系为mx,t=-ln(1-q(x,t))，在假定年龄区间内死亡服从均匀分布的前提下，Kimball（1960）[9]给出了中心死亡率与条件死亡概率的关系式：mx,t。一般的，参数若是随着时间推移而逐渐变小，则表明人口的死亡率在不断改善；参数若逐渐变大，则表明低龄人口死亡率的改善程度比高龄人口死亡率的改善程度要大；二者均服从带漂移项的随机游走。是样本年龄的平均值。

较之LC模型，CBD模型参数估计不需要死亡人数和风险暴露人数，而只需要分年龄的死亡概率值。但是，在人口死亡率统计资料中，85岁及以上高龄人口死亡率多实行末组堆积，因此，需要将高龄人口的末组死亡率进行拓展。Robine et.al（2007）[10]采用Gompertz模型、Weibull模型、Heligman-Pollard模型、Quadratic模型、Logistic模型、Kannisto模型分别对高龄人口死亡率数据进行拟合，并认为Kannisito模型拟合效果最好。黄匡时（2015）[7]也采用Kannisito模型对堆积年龄死亡率进行扩展。Kannisito模型表达式如下：

μ(x)为死亡力，a、b为待估参数，x为年龄。

用Kannisito模型外推死亡率时，需要确定死亡率外推的初始年龄。Horiuchil和Coale（1990）[11]定义了死亡力随年龄变化率k(x)（也称之为生命表老化率，即令k(x)=以k(x)值开始下降的年龄作为Kannisito模型外推死亡率的初始年龄，k(x)估计值的表达式如下：

式中mt(x,5)表示在年龄区间[x,x+5]上的该年龄组的死亡率。

k(x)的标准误近似为其中d(x,5)表示在年龄区间[x,x+5]上的该年龄组的死亡人数[12]。

总体来说，我们将分三步来预测中国0～105岁①中国保险业经验生命表极限年龄为105岁，故取到105岁，用Kannisito模型将末组堆积年龄也扩展到105岁。分性别人口的死亡率。首先，我们将运用LC模型的相干模型来预测0～89岁分年龄性别死亡率。其次，通过Kannisito模型对堆积年龄死亡率扩展到105岁后，采用CBD模型预测60～105岁分年龄性别死亡率。最后，取LC模型的相干模型预测的0～84岁分年龄性别死亡率和CBD模型预测85～105岁分年龄性别死亡率作为0～105岁分年龄性别死亡率的预测结果②。

2.生育率预测模型及方法

在人口预测中，衡量生育率常用的统计指标主要有年龄别生育率和总和生育率两种。年龄别生育率指某年一定年龄组中育龄妇女平均生育率，总和生育率指分年龄育龄妇女生育率的和。根据分析方法又可分为：队列法和时期法，虽然队列能较好地反映特定队列妇女生育史，但是时期分析法却比队列分析法更有效，因此，采用时期年龄别生育率和时期总和生育率作分析。

由于时期年龄别生育率和时间t及育龄妇女生育年龄x有关，其在形式上和死亡率模型具有一定的相似性。但是，二者还有一定的区别，Ronald D Lee（1993）[13]曾指出：生育率模型不同于对数死亡率模型，其在结构上应该是线性的。如果用fx,t表示为t年x岁育龄妇女的生育率，fx,t表达式可表示为：

其中，γx为和年龄相关的参数，反映了分年龄人口生育率的平均水平，φx表示年龄x对生育率的敏感度；ηt为和时间相关的参数，这里可看作生育指数，反映人口生育随时间变化的速度；μx,t为误差项，其均值为0且方差为

模型参数φx、ηt在估计要得到唯一解，需做以下假定：

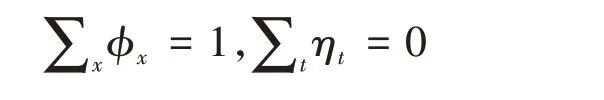
在上述假定基础上，γx的估计值可以看作各年龄育龄妇女生育率在时间t上的平均值，即γ^x=。

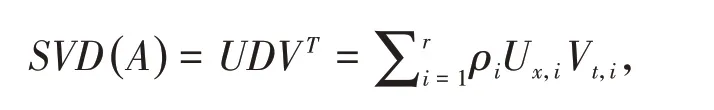
其中，U和V为正交矩阵，D为对角矩阵，其对角元素ρi(i=1,…,r)为矩阵Ax,t的有序奇异值（按递减顺序排列），r为矩阵Ax,t的秩。

由于第一个奇异值ρ1比其他的奇异值要大得多，因此矩阵，结合上述φx、ηt参数估计的约束条件，φx、ηt标准化处理后的估计值分别为：。对估计的ηt序列值再利用ARIMA模型拟合，可得ηt的预测值；最后，利用参数γx、φx估计值和ηt的预测值代入式（9）即可对分年龄生育率进行预测。按照式（9）总和生育率（TFRt）可表示为TFRt=。

3.参保率预测模型及方法

同样，按国发〔2014〕8号文件规定，计算满16周岁（不包括在校学生）及以上的、可以参加城乡居保的人，按其年龄分段并计算总参保率。总体思路为：首先，测算2012～2017年①因新农保从2009年开始试点，城居保从2011年开始试点，故分析城乡居民养老保险的参保率选择从2012年开始。全国可以参加城乡居保的16～59岁人数和60岁及以上人数。其次，计算2012～2017年城乡居保的参保缴费（16～59岁）人数和可以领取待遇年龄（60岁及以上）人数②指参加城乡居民养老保险的个人，年满60周岁、累计缴费满15年，且未领取国家规定的基本养老保障待遇的，以及新农保或城居保制度实施时已年满60周岁的。。最后，用分年龄段的参保人数除以相对应年龄段的符合参保条件的人数，结果即为分年龄段总参保率。总参保率预测采用华中理工大学邓聚龙教授（1996）[14]提出的GM（1，1）模型来分析，在此基础上进一步采用规划求解的方法来获得分年龄参保率。具体计算方法和结果见许燕和杨再贵（2019）[15]。本文中对计算结果进行了数据更新，加入了2017年的数据。

（三）符合城乡居保条件的期初人数测算及相关假定

首先，根据资料的可得性，选取t0=2017年人口数据为基年数据。由《2018中国统计年鉴》中的实际人口数和《2018中国人口和就业统计年鉴》中全国分年龄、性别抽样人口数即可求得2017年全国分年龄、性别的实际人数。根据经验生命表的最高年龄，这里我们也假设存活极限年龄为105岁。因《2018中国人口和就业统计年鉴》中全国分年龄、性别抽样人口数的末组年龄为95+，故需要对95岁及以上分性别人口数进行拆分，在这通过引入条件生存概率S(x*-j)①条件生存概率这里x*=95，所以条件生存概率可表示成：S(95-j)=其中j∈［0，20］的整数，∞D95-j表示死亡年龄在95-j岁及以上的人数之和）。的形式，即从x*-20存活到x*-j。用生存函数s(x)②生存函数s(x)=，文中x0=75岁，则。对该经验数据进行拟合，在残差平方和最小的情况下，利用规划求解可得s(x)中的参数a0、b0估计值，进一步可推导95岁的人数为[s^(95)-s^(96)]·∞D75，余者依次类推，可完成堆积在95岁的分性别人口的拆分。然后，根据2017年拆分的男女0～105岁的抽样人数占比乘以2017年分年龄性别实际总人口数，可以得到分年龄性别的实际人口基数。

其次，求全国16岁及以上的分年龄在校学生数。根据《2018中国统计年鉴》披露的2017年在校学生数，按现行普遍的学制（小学6年、初中3年、高中及职业教育3年、本科4年、研究生3年）来划分在校学生的年龄段。然后分别按全国相同年龄段抽样人口数计算各年龄人口占比，再用该占比乘以相应年龄段的在校学生数，得到2017年全国16岁及以上的分年龄在校学生数。在人口预测时，假定相应年龄段的在校学生数占全国同年龄段人口比例保持不变。

最后，求机关事业单位人员数和企业职工人数。虽然机关事业单位和企业实行相同的养老保险制度，但是，在现实情况中，二者的入职年龄和退休年龄依然存在一定的差异。根据现有的实际情况及《中华人民共和国劳动法》的规定，我们将对机关事业单位和企业职工的入职年龄和退休年龄做出如下一系列的假定。关于入职年龄，一般的我们假定机关事业单位的入职年龄为23岁（不分男女）、企业职工的入职年龄为20岁（不分男女）。关于退休年龄，假定机关事业单位男性职工退休年龄为60岁、女性职工退休年龄为55岁，假定企业职工男性退休年龄为60岁、女性为50岁。与此同时，假设2016年机关事业单位人员和企业职工分年龄、性别占比同全国分年龄、性别抽样人口数，乘以机关事业单位和企业在职及退休人数，得到2016年分年龄性别机关事业单位和企业人数。在人口预测时，假设每年机关事业单位新入职职工人数占全国23岁总人口比重保持2017年的比例不变，每年企业新入职职工人数占全国20岁总人口比重保持2017年的比例不变。

在此基础上，根据上述分年龄死亡率、生育率及参保率的预测，结合式（1）至式（4）可完成城乡居保参保人数预测。

四、城乡居保人口预测指标参数结果分析

（一）死亡率模型参数及预测结果分析

分年龄死亡率样本数据来源于《中国人口统计年鉴》（1996～2007）和《中国人口和就业统计年鉴》（2008～2018）中合计23年的数据。这23年的样本数据长短不一致，其中1996年末组年龄为85+，而1995年、2000年、2005年、2010年与2015年的末组年龄为100+，其余年份的末组年龄均为90+。根据分析问题，对1996年末组堆积在85+的抽样死亡人数数据按Wilmoth（2007）①Wilmoth J R，Andreev K，Jdanov D，Glei D A.Methods Protocol for the Human Mortality Database.University of California［R/OL］，Berkeley（USA）and Max Planck Institute for Demographic Research，Rostock（Germany）2007，http：//www.mortality.org or http//www.human mortality.de.提出的方法扩展到90+，然后，选取了1995至2017年的0～89岁的分性别及不分性别死亡率样本数据，利用R软件编程，对23年的分年龄死亡率样本数据采用MLE方法进行估计，得到估计参数αx（分性别与混合）、βx和κt（混合）如图2～图4所示。

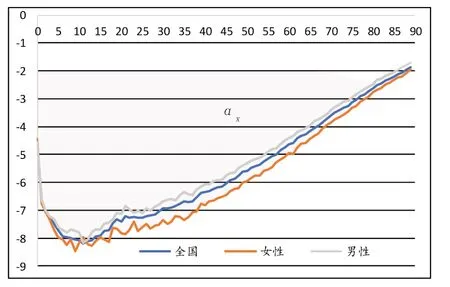
图2 参数αx（分性别及混合）估计值

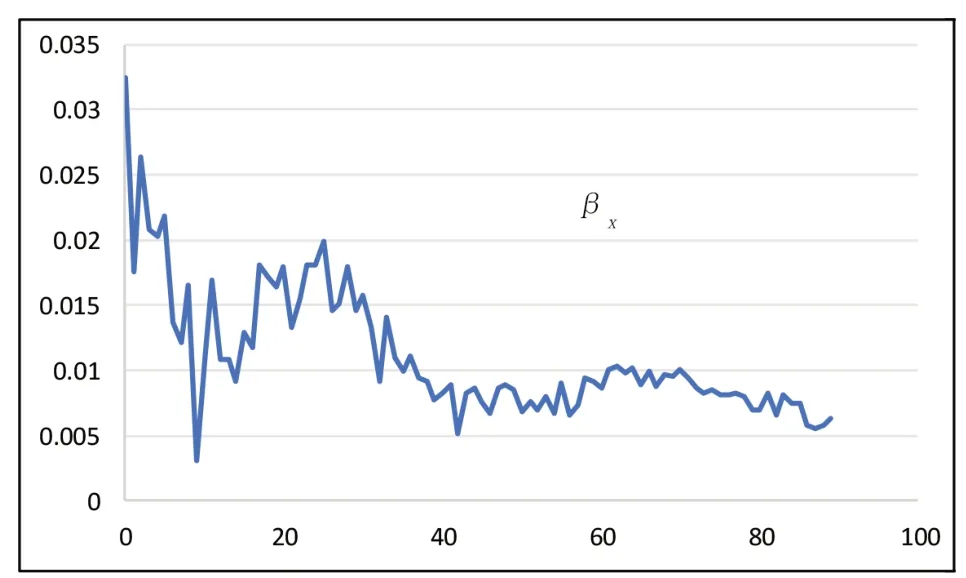
图3 参数βx估计值

图4 参数κt估计值

κt估计值经过1次差分后得到平稳时间序列，进一步对κt估计值的一阶差分序列进行自相关和偏自相关检验，对κ^t用ARIMA（p，1，q）模型，依据残差平方和最小及AIC准则及其模型系数的显著性，选取ARIMA（1，1，0）模型，对模型拟合的残差进行Q统计检验，结果通过，得到死亡率模型参数κt的预测值表达式为：

式（10）括号中的值为标准误。根据估计的参数αx、βx和κt，采用LC相干模型可预测2018年及以后年份0～89岁的分性别死亡率。

其次，根据生命表老化率值，选取65岁（不分男女）作为初始年龄，用Kannisito模型将1995～2017年分年龄性别死亡率扩展到105岁，采用CBD模型分别求得1995～2017年的60岁及以上年龄人口的和，具体如图5和图6所示。

图5 CBD模型1995～2017年的60岁及以上男、女的值

图6 CBD模型1995～2017年的60岁及以上男、女的值

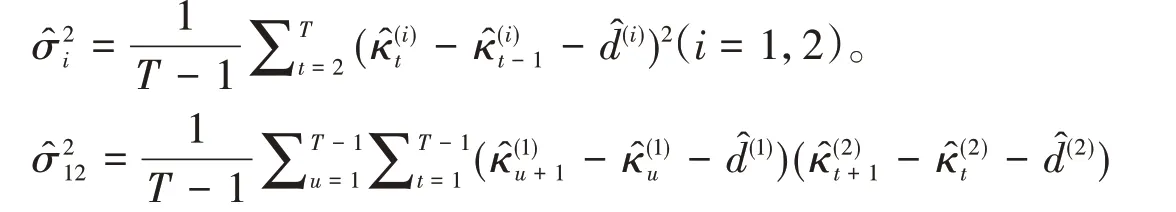
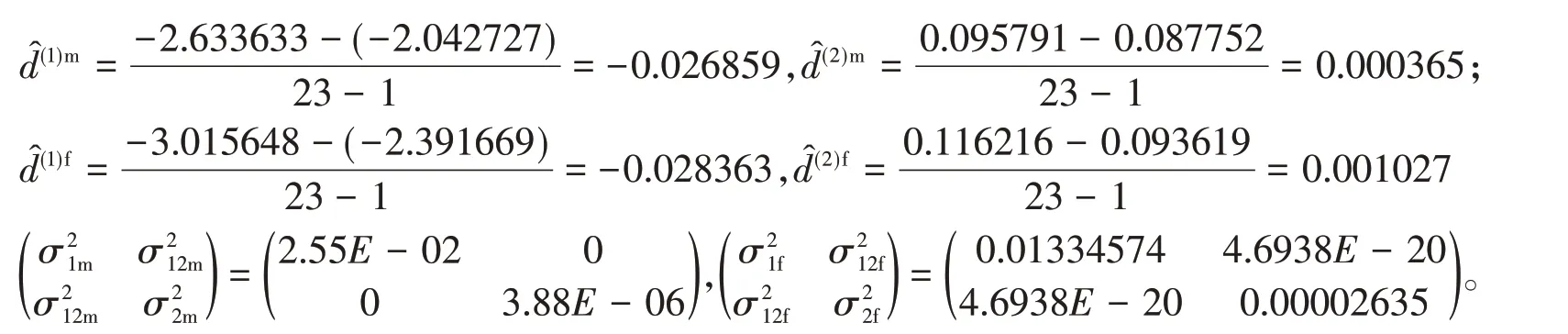
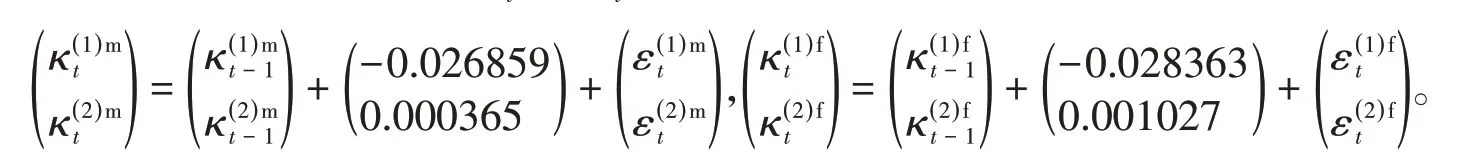
最后，取LC相干模型中0～84岁人口的死亡率的预测值和CBD模型中85～105岁人口的死亡率的预测值相结合，即可得0～105岁人口死亡率的预测值。根据死亡率的预测值可计算预测各年的0岁男女的预期寿命①t年x岁的人预期剩余寿命计算公式为其中ω为极限寿命。，到2029年我国男性城乡居民人口预期寿命约为81.18岁，女性城乡居民人口预期寿命约为84.99岁，由预期寿命，假设我国城乡居民死亡率收敛于2029年②统计资料显示：2018年日本男性的平均预期寿命为81.25，女性的平均预期寿命为87.32，考虑到我国与日本经济发展水平及人民生活水平的差异，故假设死亡率值收敛于2029年。，篇幅所限，这里只列示女性死亡率预测值对数值，结果如图7所示。

（二）生育率相关参数及预测结果分析

采用的1997～2017年分年龄生育率原始数据。其中，2005年及以前年份的数据源自《中国人口统计年鉴》，2006年及以后年份的数据来源于《中国人口和就业统计年鉴》，其中2000年数据来自“五普”，2010年数据来自“六普”，总共21年的样本数据。

这21年的样本数据涉及两个问题需要处理：一是样本数据中平均育龄妇女总人数抽样统计数量级不统一。样本数据中2000年和2010年的平均育龄妇女抽样统计总人数数量级为千万人，2005和2015年的平均育龄妇女抽样统计总人数数量级为百万人，而其余年份平均育龄妇女抽样统计总人数数量级均为十万人，为此，我们将2000年 和2010年 及2005和2015年这4年的平均育龄妇女抽样统计总人数数量级均调整为十万人。二是部分年份中15岁育龄妇女对应的出生人数和生育率数据缺失。在这21年的样本数据中缺少1998年、1999年、2007年和2012年的15岁育龄妇女对应的出生人数和生育率数据。针对生育率数据的缺失，文中利用其余年份的15岁育龄妇女对应的平均生育率数据对其进行插值补齐；缺失的出生人数则可根据生育率和相应年份的15岁育龄妇女人数求得。

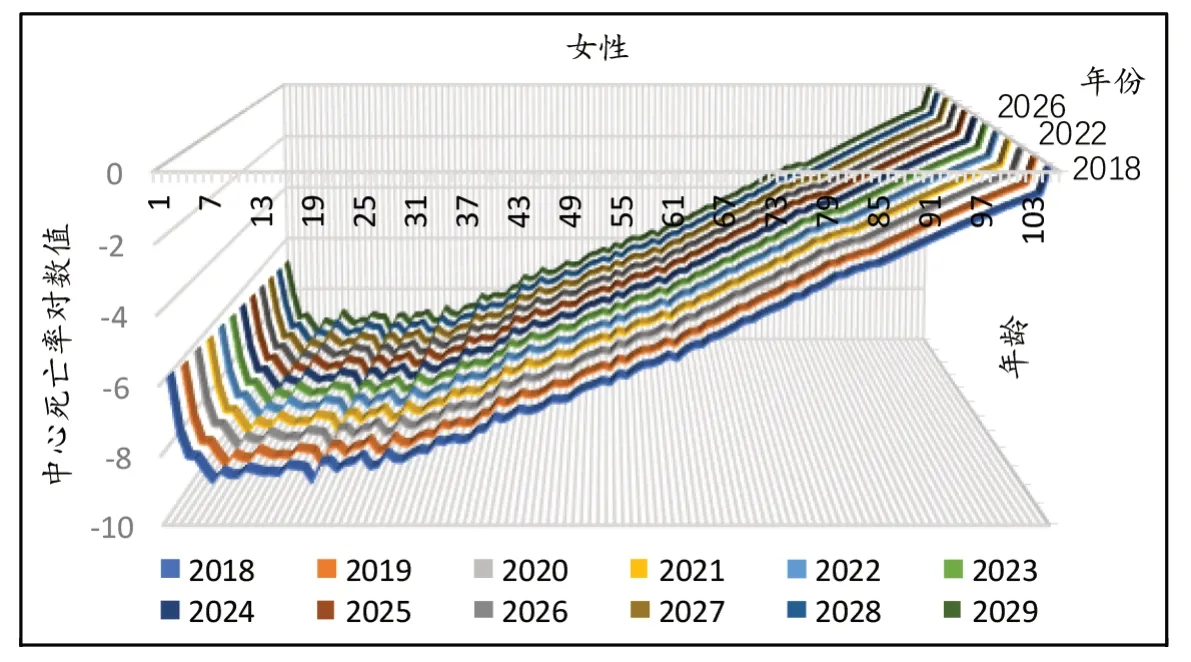
图7 2018～2029年女性ln mx值

同样利用R进行编程，采用SVD方法来估计模型中的参数γx、φx和ηt。得到估计参数γx、φx和ηt的估计值，其中γx、ηt值如图8和图9所示。

图8 参数γx估计值

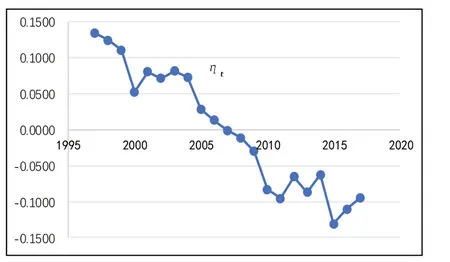
图9 参数ηt估计值

由图8可知，24岁为我国妇女的育龄峰值。

对ηt的处理过程类同于死亡率中的κt，经一阶差分后得到平稳序列，对此序列进行自相关、偏自相关检验，无截尾，采用ARIMA（0，1，0）模型，得到生育率模型参数ηt预测值的表达式为：

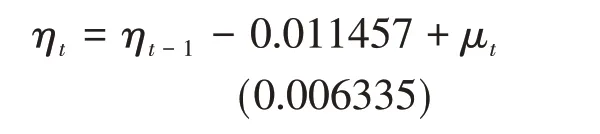
括号中的值为标准误。从ηt值的走势可以看出，1997～2017年我国生育率水平总体基本呈持续下降的发展趋势，2015年达到最低水平，之后又稍有回升。这种持续走低的生育率水平和人们的生育观念的转变、国家生育政策的制定等多种因素有关。生育率水平在2015年以后的轻微反弹，应主要归因于我国政府生育政策的调整。2015年10月“全面二孩”政策对改善我国当前人口结构，缓解我国生育率持续下降起到了一定的作用。但是，由于受到历史样本数据的影响，ηt的预测值呈现出持续下降的趋势，基于对生育政策未来的预期，对所预测的2018～2056年分年龄生育率水平进行修订，2020年以前采用预测的分年龄生育率水平，2020年以后假定生育率水平保持在2020年不变。

（三）参保率的预测

1.2012～2017年分年龄段的参保率

根据计算的城乡居保的总参保人数和达到领取待遇年龄参保人数除以对应年龄段的符合城乡居保参保条件的人数，从而可计算出城乡居保的缴费人群和领取待遇人群的分年龄段的相应年份的总参保率。结果如下表1所示：

表1 2012～2017年城乡居民养老保险分年龄段的参保率

以表1中16～59岁年龄段的参保率为基础，用6维数据，通过GM（1，1）模型预测得到的该年龄段的参保率预测值如表2所示：

表2 16～59岁缴费人群总参保率的预测值（%）

2.16～59岁分年龄的参保率

以下以2017年16～59岁参保人数数据为例，通过规划求解方法，得到结果如下表3所示：

表3 2017年城乡居民养老保险缴费人群分年龄参保率 单位：%

其中规划求解得2017年的α=475301.3234、β=0.4135和y=33.3，即2017年16～59岁城乡居民养老保险总参保率69.83%代表年龄约为33.3岁。有了分年龄参保率则可进一步对城乡居民养老保险参保人数进行预测。

（四）城乡居保参保人数预测结果

1.全国人口基数测算

根据《中国统计年鉴》（2018）中的实际人口数和《中国人口和就业统计年鉴》（2018）中全国分年龄、性别抽样人口数可求得2017年全国分年龄、性别的实际人口数，并以此为实际人口基数。

因《中国人口和就业统计年鉴》（2018）中全国分年龄、性别抽样人口数公布的抽样人口的末组年龄为95+，在假设生存极限年龄为105岁的情况下，引入条件生存概率对95岁以上分性别的末组年龄人口进行拆分，得到分年龄性别人口占总抽样人口的比值，结果如表4所示。

表4 2017年分年龄性别人口占比（%）

将表4中的分年龄性别人口占比乘以年鉴中2017年全国实际总人口数，可求得2017年全国分年龄、性别的实际人口数，并以此为实际人口基数，结果如图10所示。

根据3.3节中假定，即预测年份t年16岁及以上分年龄性别的在校生数、机关事业单位人数和企业职工人数占全国同龄人口数的比与2017年相应人口占全国同龄人口数的比相同，结合2017年在校生数、机关事业单位人数和企业职工人数以及全国分年龄、性别的实际人口数，可以得到和值如表5所示。

2.可参加城乡居保的人数预测

根据2017年的女性15～49岁的实际人口数，结合式（1）及男女婴儿性别比，可计算2018年0岁分性别出生人口数。再依据2017年分年龄性别的实际人口数，结合式（2），则可计算出2018年1～105岁分性别的实际人口数。依次类推，从而可完成历年的全国分年龄性别实际人数的预测。

用预测的16～25岁全国分年龄性别实际人口数乘以对应年龄的则可完成对历年在校生的人口预测。

图10 2017年全国分年龄、性别的实际人口数

表5 t年16～25岁在校生数、23岁机关事业单位人数和20岁企业职工人数占全国同龄人比

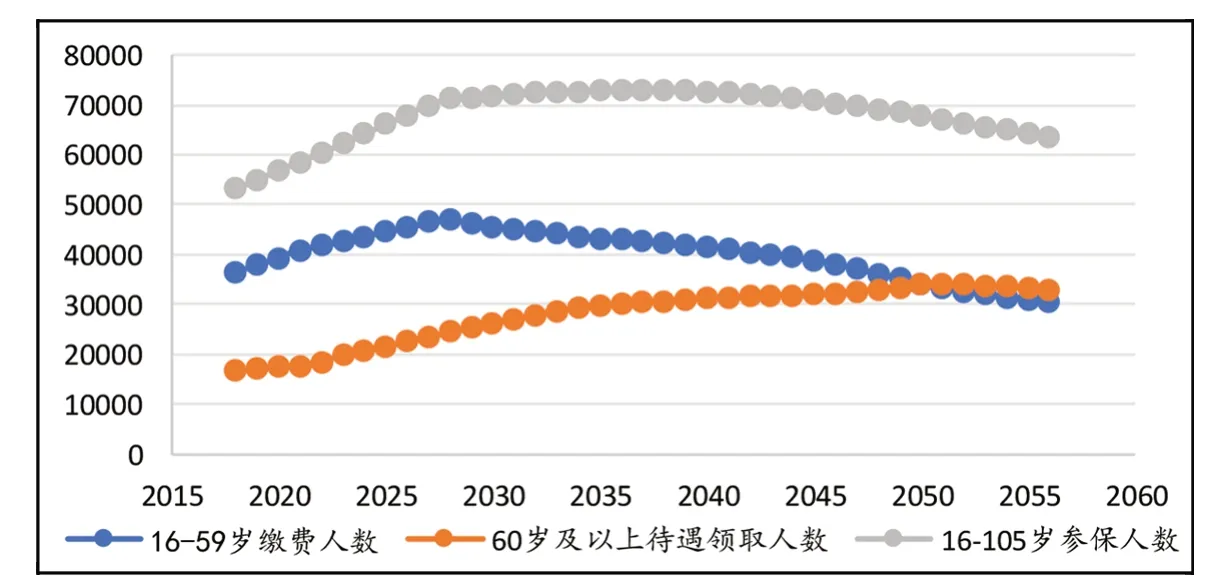
图11 2018～2056年参加城乡居保的人数

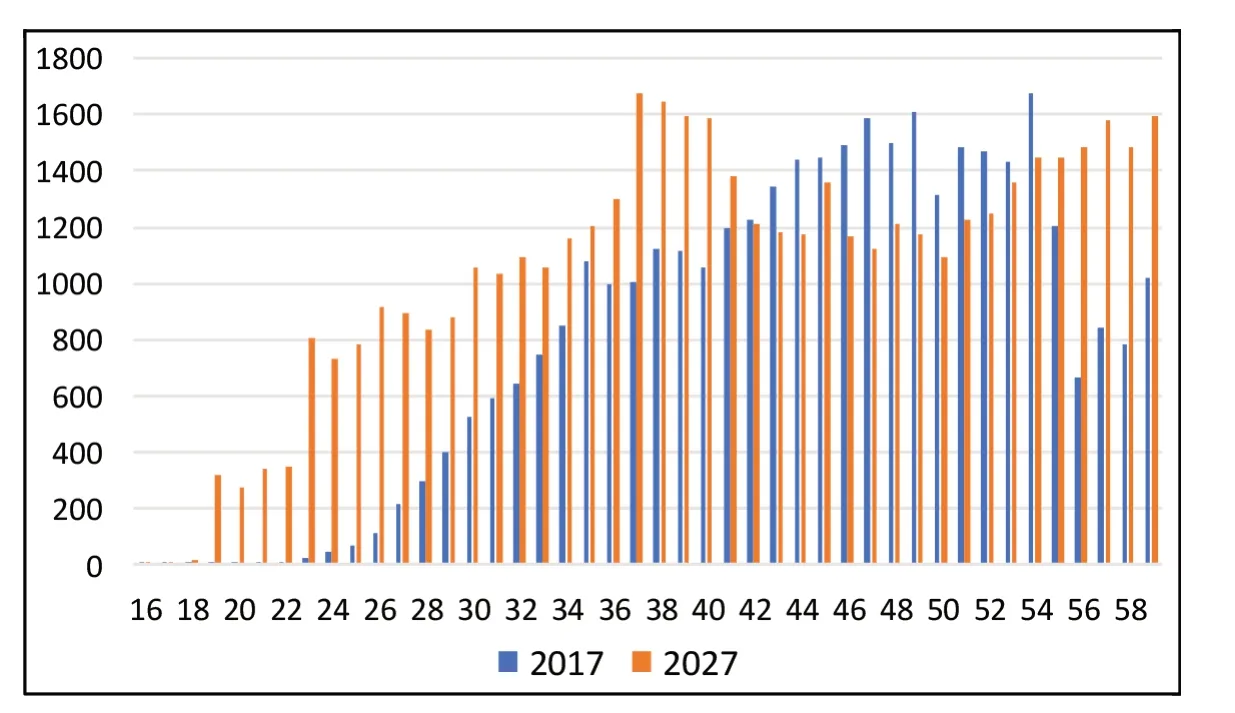
图12 2017年、2027年城乡居保16～59岁缴费人数

在上述人口预测基础上，按国发〔2014〕8号文件规定对学生数和参加城镇职工养老保险的人数进行相应的扣除，结合式（3）则可得预测年份16～105岁符合参保条件的人数，则可得到历年的符合城乡居保参保条件的预测人口数。

3.城乡居民养老保险参保人数的预测

得到预测年份16～105岁符合参保条件的人数以后，进一步的，根据式（4）和表2中的数据则可预测历年城乡居保总缴费人数和总领取待遇人数，结果如图11所示。

根据规划求解的16～59岁分年龄参保率还可以测算出预测年份分年龄缴费人数。比如2017年、2027年分年龄参保缴费人数如图12所示。

五、结论与政策启示

（一）结论

通过对城乡居保的参保人数预测，得出了如下四个主要结论：

首先，从全国人口及男女人口分年龄死亡率预测结果来看，中国男女人口死亡率均有所改善，人口的平均预期寿命将越来越高。

其次，就我国育龄妇女生育率水平分析来看，因实行全面二孩政策，2015年以后生育率水平有所回升，但是受历史样本数据的影响，预测年份生育率水平总体上依然呈下降趋势。

再次，通过对城乡居保参保率的分析，结果发现：城乡居保的参保率呈逐年上升趋势，越来越多的城乡居民选择参加城乡居保，而且代表年龄的参保率呈现出越来越低的趋势，根据计算，2017年约为33.3岁，到2027年则约为21.9岁，表明人们越来越意识到参加养老保险的重要性，这也说明制度化的养老保险功能在日益增加。

最后，根据所预测的2018～2056年参加城乡居保人数的结果，不难发现：16～59岁的缴费人数开始呈不断上升的趋势，在2028年达到了峰值，其后又开始逐年下降；60岁及以上领取待遇人数在预测区间内呈现出逐年递增的趋势，并在2051年出现了缴费人数少于领取待遇人数的情况。因此，从城乡居保参保人数来看，随着人口的逐步老龄化，政府对城乡居保的财政负担也将会逐年增加。

（二）政策启示

从上述研究结论中可以得到如下三个方面的启示：一方面，随着中国人口死亡率的改善和育龄妇女生育水平的下降，我国人口在发展中呈现出少子化、老龄化的趋势。因此，要改善城乡居保参保人口结构，有必要出台一些鼓励生育的措施，比如对生育二孩的家庭根据其收入水平来给予适当的奖励，或者发放生育补贴、营养补贴、奶粉费及幼儿教育费等。只有不断提高生育意愿，改善人口结构，才能在较长时期内，从一定程度上缓解城乡居保人口老龄化。另一方面，城乡居保参保制度给中国数亿人口提供了一种制度化的养老模式。从城乡居保参保率来看人们的参保意识在逐渐增强，对制度化的养老需求越来越高。最后，随着缴费人数少于领取待遇人数的到来，可小步渐进适当提高领取待遇的最低缴费年限。

本文所做的城乡居保参保人数预测可起到一个抛砖引玉的作用，在此基础上还能进一步分析未来城乡居保财政保障能力和个人账户支付缺口，进而考察城乡居保制度的财务可持续性的问题。