GPS/Galileo/QZSS精密单点定位精度分析

宋大鹏，李玉海，崔素梅，罗翠翠，郭秋英

（1.山东正元数字城市建设有限公司，山东 烟台 264000；2.山东建筑大学 测绘地理信息学院，山东 济南 250000）

进入21世纪以来，全球的卫星导航与定位系统发展迅速，较成熟的系统包括美国的GPS、欧盟的Galileo、俄罗斯的GLONASS、中国的BDS以及日本的QZSS[1-2]。其中，GPS建设时间和为全球用户提供导航与定位服务最早，Galileo于2016年正式开始提供服务，QZSS于2018年初正式向亚太地区提供服务，这3个系统均设计了兼容频率，随着全球卫星导航与定位系统的不断发展，多系统多频组合定位将是今后研究的重点[3-4]。精密单点定位技术采用单台接收机，基于IGS机构发布的精密星历与钟差产品，经过各项误差改正，利用载波相位观测值实现快速高精度静态定位，现已被广泛应用于多个领域[5]。虽然精密单点定位技术应用广泛，但仍存在部分不足与需要进一步研究的方向，如恶劣环境下的精密单点定位精度和收敛时间、多系统多频组合的精密单点定位性能等[6]。针对上述不足，很多学者进行了研究，如吕伟才[7]等发现滤波后的模糊度固定比浮点解水平方向和高程方向均有较大提升，而滤波后的静态与仿动态精密单点定位的收敛时间比浮点解也有较大提升；赵兴旺[8]等发现在进行单双频实时静态与动态精密单点定时，GPS/Galileo比GPS单系统在E、N、U方向的定位精度有较大提升，收敛时间也有了较大改善；李林阳[9]等发现Galileo卫星可见数不足GPS卫星的一半，随着卫星可见数的增加，定位收敛时间不断缩短，随着观测时间的增加，其定位精度不断增加，但整体状况比GPS差；杨行言[10]等发现在澳大利亚地区GPS与GPS/BDS的实时精密单点定位精度和收敛时间相当，BDS比二者略差，水平方向和高程方向精度分别为10 cm和20 cm，收敛时间分别为25 min和30 min。

为进一步分析多系统多频组合精密单点定位性能，本文基于日本地区的IGS跟踪站数据，分析了GPS、Galileo、GPS/QZSS、GPS/Galileo、Galileo/QZSS 和GPS/QZSS/Galileo共6种情况下的卫星可见数、PDOP值、精密单点定位精度以及收敛时间。

1 精密单点定位模型

在精密单点定位中，通常采用的模型是消电离层模型，可消除一阶电离层的影响。消电离层伪距和载波相位观测值的计算公式为：

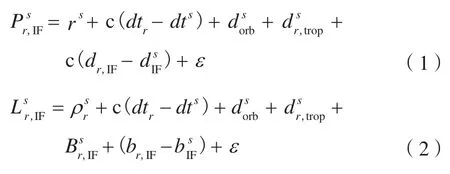
式中，IF为无电离层组合；P为伪距观测值；L为载波相位观测值；ρ为站星间距；c为真空中光速；dtr为接收机钟差；dts为卫星钟差；为卫星轨道误差；为对流层延迟；dr,IF为接收机硬件延迟；为卫星硬件延迟；ε为改正误差和噪声；B为整周模糊度；br,IF为接收机端相位延迟；为卫星端相位延迟。

根据式（1）、式（2）构建双系统组合模型，则有：

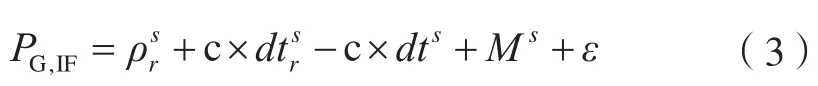
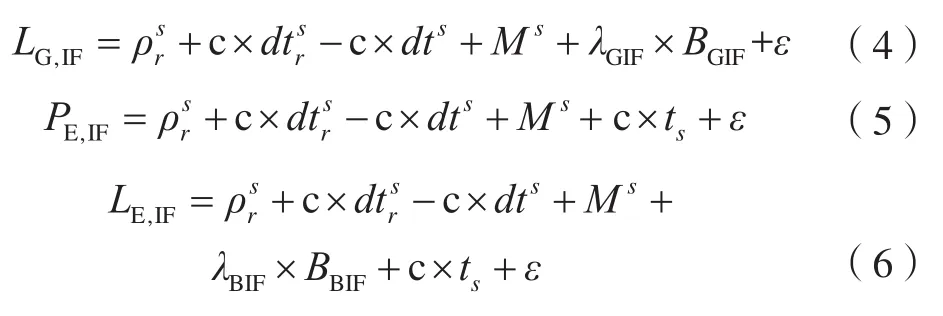
式中，G为GPS；E为Galileo；λ为无电离层组合波长；ts为GPS与Galileo的时间偏差。

三系统组合采用UD模型，即根据无电离层观测值进一步组合而成，计算公式为：

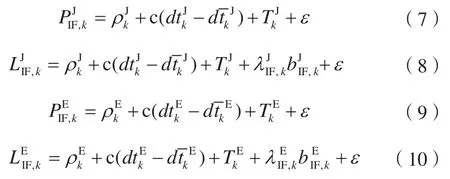
式中，J为QZSS。

2 数据处理分析

2.1 数据处理方案

实验数据选用MEGX发布的位于日本地区的CCJ2站数据，观测时间为2019-05-01－05-06共7 d，数据采样率为30 s，可同时接收GPS、Galileo、QZSS三个系统的观测数据。实验利用根据RTKLIB改进的程序进行数据解算，设计了两种解算方案：①对 GPS、Galileo、GPS/Galileo、GPS/QZSS、Galileo/QZSS以及GPS/Galileo/QZSS共6种组合下的数据进行静态精密单点定位处理；②对GPS、Galileo、GPS/Galileo、GPS/QZSS、Galileo/QZSS 以及GPS/Galileo/QZSS共6种组合下的数据进行动态精密单点定位处理，再将解算得到的7 d数据结果取平均值作为最终的分析结果。6种组合下的卫星可见数与PDOP值如图1、2所示，其中G表示GPS、E表示Galileo、J表示QZSS。

由图1可知，Galileo的卫星可见数在6种组合中最少，只有4～7颗；GPS与Galileo/QZSS的卫星可见数相当，约为5～12颗；GPS/QZSS与GPS/Galileo的卫星可见数相当，约为6～16颗；GPS/QZSS/Galileo的卫星可见数最多，为15～22颗。由图2可知，Galileo的卫星空间分布结构最差，平均PDOP值为3.74；其次是GPS，平均PDOP值为2.04，组合的PDOP值比单系统有明显减小，Galileo/QZSS的平均PDOP值为1.87，GPS/QZSS的平均PDOP值为1.55，GPS/Galileo的平均PDOP值为1.49，GPS/QZSS/Galileo的平均PDOP值为1.26。

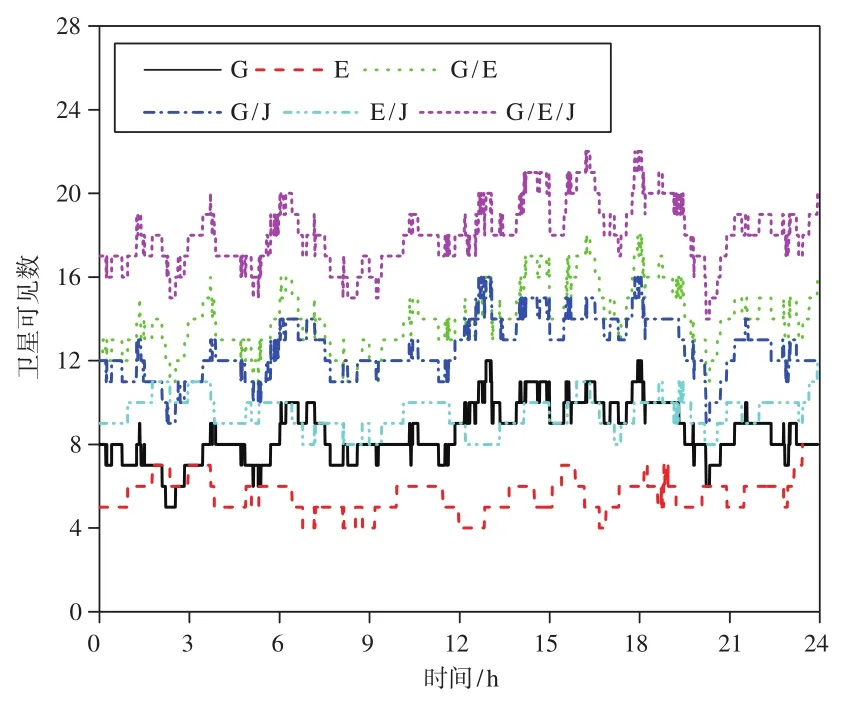
图1 卫星可见数

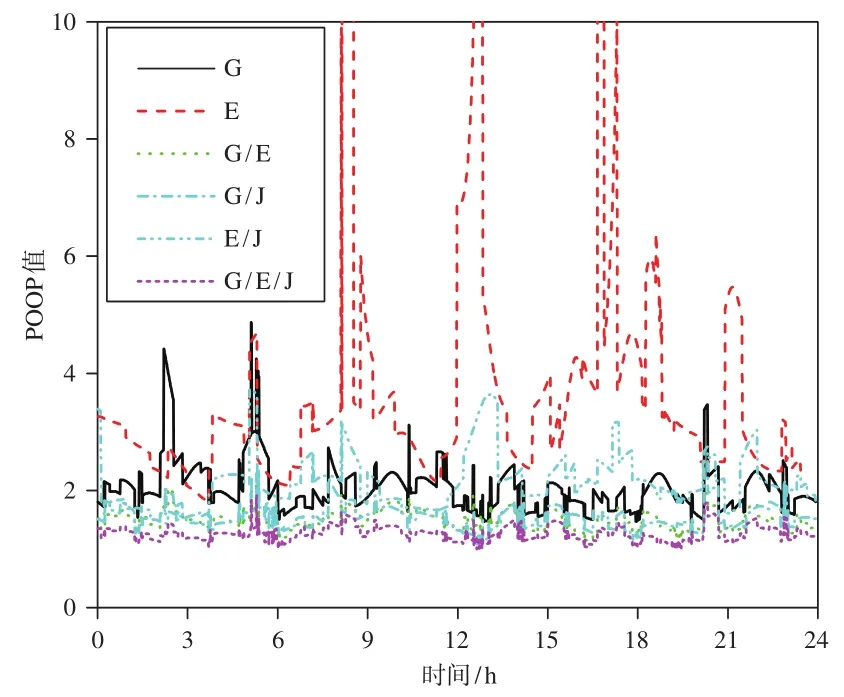
图2 PDOP值

2.2 静态精密单点定位

在进行静态精密单点定位数据处理时，高度角设置为7°，采用武汉大学发布的精密星历与钟差产品，直接从武汉大学IGS中心官网下载，计算得到方案①中6种组合下的精密单点定位误差序列、RMS值和首次收敛时间，如图3～5所示。收敛时间是指3个方向坐标误差连续20个历元都小于0.1 m。

由图3可知，6种组合下静态精密单点定位3个方向的误差在开始时均出现较大波动，GPS、Galileo、GPS/Galileo、GPS/QZSS、Galileo/QZSS和GPS/Galileo/QZSS分别在观测5 h、6 h、4.7 h、4.6 h、4.3 h和3.5 h后3个方向的定位误差稳定在0.1 m以内；且双系统组合的精密单点定位误差波动小于单系统，而三系统组合定位误差波动小于双系统，误差稳定时间也随着系统的增加而缩短。

由图4可知，单系统静态精密单点定位时，GPS精密单点定位在E、N方向的RMS值小于Galileo，U方向的RMS值与其相当，E方向的RMS值为1.91cm，N方向的RMS值为1.56cm，U方向的RMS值为3.61cm；双系统组合中GPS/Galileo组合3个方向的RMS值最小，E方向的RMS值为1.41cm，N方向的RMS值为1.35cm，U方向的RMS值为1.92cm；GPS/Galileo/QZSS三系统组合比双系统组合3个方向的RMS值明显减小，E方向的RMS值为0.68cm，N方向的RMS值为1.11cm，U方向的RMS值为1.55cm。GPS/Galileo/QZSS三系统组合比单系统中RMS值最小的GPS系统E、N、U方向的RMS值分别减小了64.3%、28.8%和56.9%，比双系统组合中RMS值最小的GPS/Galileo组合E、N、U方向的RMS值分别减小了51.7%、17.8%和19.3%。

由图5可知，随着组合系统的增加静态精密单点定位3个方向的收敛时间不断缩短，单系统中GPS的收敛时间最短，E方向的收敛时间为25 min，N方向的收敛时间为23 min，U方向的收敛时间为31 min；而双系统组合中除Galileo/QZSS组合外另两种组合收敛时间优于单系统，最明显的是GPS/Galileo，E方向的收敛时间为15 min，N方向的收敛时间为16 min，U方向的收敛时间为24 min；GPS/Galileo/QZSS三系统组合收敛时间比任意双系统组合短，E方向的收敛时间为12 min，N方向的收敛时间为11 min，U方向的收敛时间为15 min。GPS/Galileo/QZSS三系统组合比单系统中收敛时间最短的GPS系统E、N、U方向的收敛时间分别缩短了52.0%、52.2%和51.6%，比双系统组合中收敛时间最短的GPS/Galileo组合E、N、U方向的收敛时间分别缩短了20.0%、31.3%和37.5%。

2.3 动态精密单点定位

动态精密单点定位的处理策略、采用的精密产品以及分析对象与静态精密单点定位一致。

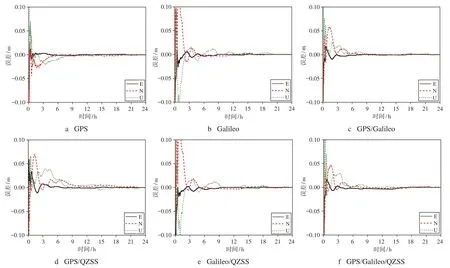
图3 静态精密单点定位误差序列

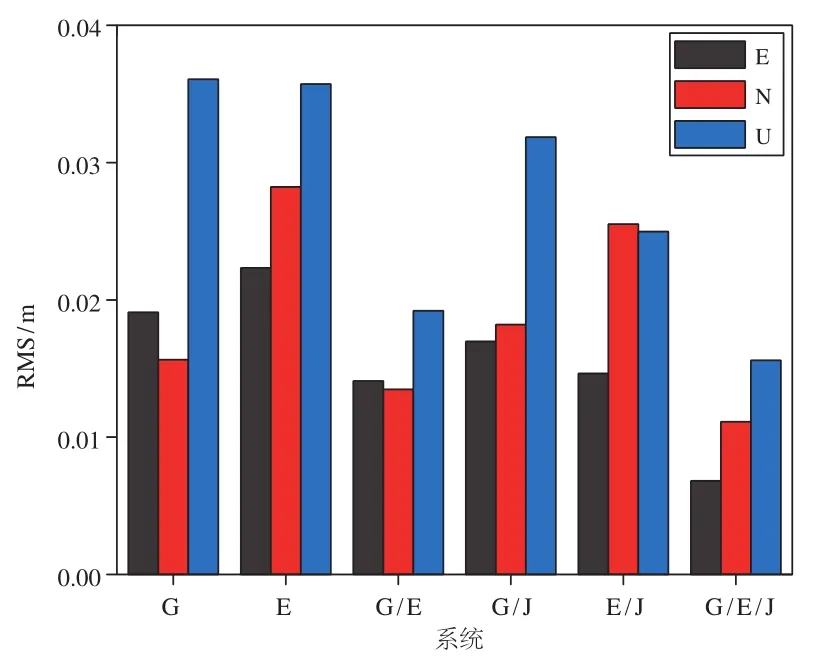
图4 静态精密单点定位RMS值

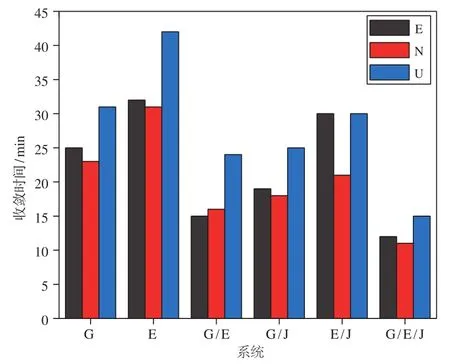
图5 静态精密单点定位收敛时间

由图6可知，动态精密单点定位E、N、U方向的误差波动远远大于静态精密单点定位，E、N方向误差在收敛后趋于稳定，而U方向误差在观测时段内变化较大。在单系统中，GPS三个方向的误差变化小于Galileo，E、N方向收敛后优于1cm，而U方向误差在0.2m之内变化；双系统组合比单系统定位误差小，GPS/Galileo和GPS/QZSS组合的E、N方向收敛后优于1cm，而U方向误差在0.15 m之内变化，Galileo/QZSS组合的E、N方向收敛后优于3cm，而U方向误差在0.4m之内变化；三系统组合比双系统组合定位误差小，GPS/Galileo/QZSS组合的E、N方向收敛后优于1cm，而U方向误差在0.1 m之内变化。

由图7可知，单系统中GPS动态精密单点定位的RMS值小于Galileo，E方向的RMS值为3.15cm，N方向的RMS值为2.2cm，U方向的RMS值为7.22cm；双系统组合中GPS/Galileo组合3个方向的RMS值最小，E方向的RMS值为2.59cm，N方向的RMS值为1.32cm，U方向的RMS值为5.33cm；GPS/Galileo/QZSS三系统组合比双系统组合3个方向的RMS值小，E方向的RMS值为0.91cm，N方向的RMS值为1.14cm，U方向的RMS值为3.79cm。GPS/Galileo/QZSS比单系统中RMS值最小的GPS系统E、N、U方向的RMS值分别减小了71.1%、48.2%和47.4%，比双系统组合中RMS值最小的GPS/Galileo组合E、N、U方向的RMS值分别减小了64.9%、13.6%和28.9%。

由图8可知，动态精密单点定位收敛时间长于静态精密单点定位，单系统中GPS的收敛时间最短，E方向的收敛时间为31min，N方向的收敛时间为28min，U方向的收敛时间为40min；双系统组合定位收敛时间短于单系统，最短的是GPS/Galileo组合，E方向的收敛时间为23min，N方向的收敛时间为20min，U方向的收敛时间为31min；GPS/Galileo/QZSS三系统组合比任意双系统组合的收敛时间短，E方向的收敛时间为13min，N方向的收敛时间为10min，U方向的收敛时间为16min。GPS/Galileo/QZSS三系统组合比单系统中收敛时间最短的GPS系统E、N、U方向的收敛时间分别缩短了58.1%、64.3%和60.0%，比双系统组合中收敛时间最短的GPS/Galileo组合E、N、U方向的收敛时间分别缩短了43.5%、50.0%和48.4%。

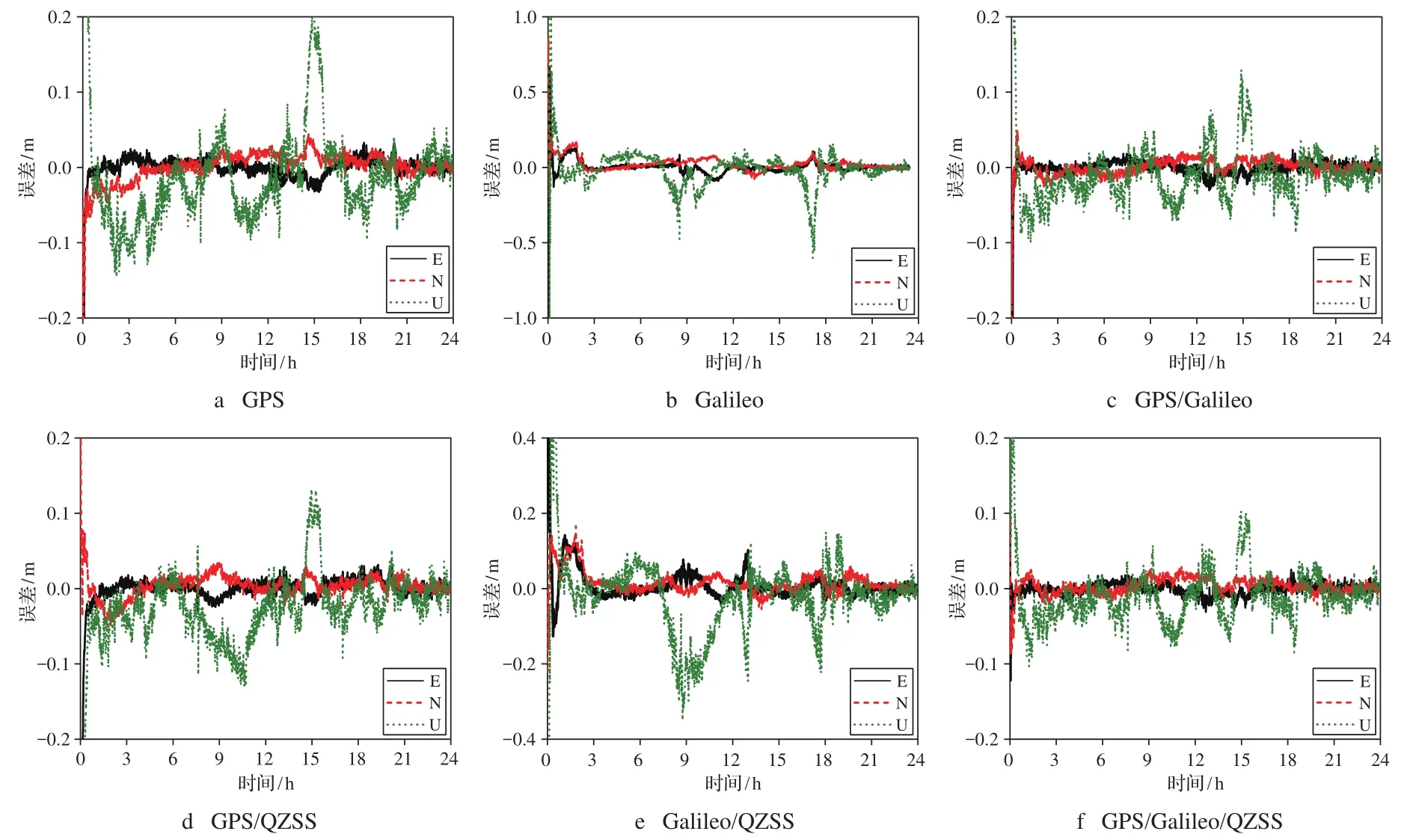
图6 动态精密单点定位误差序列

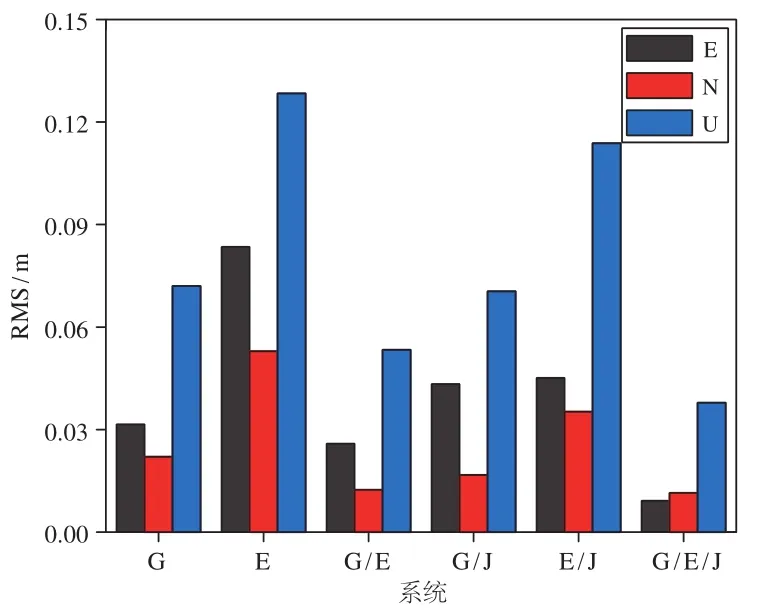
图7 动态精密单点定位RMS值

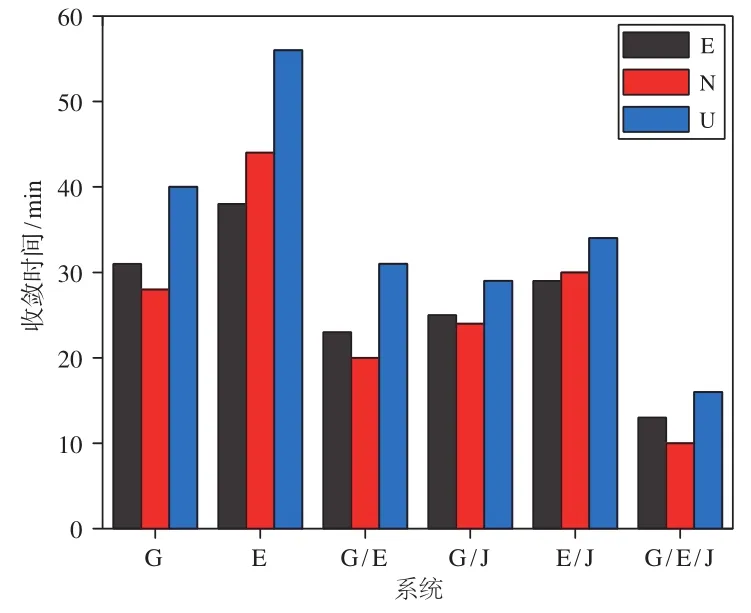
图8 动态精密单点定位收敛时间

3 结 语

针对多系统组合精密单点定位性能，本文基于CCJ2站连续7 d的观测数据，分析了GPS、Galileo、GPS/QZSS、GPS/Galileo、Galileo/QZSS和GPS/QZSS/Galileo组合下的静、动态精密单点定位精度与收敛时间，主要结论为：

1）相较于单系统与双系统组合，GPS/Galileo/QZSS三系统组合的卫星可见数明显增加，PDOP值明显减小。

2）在静态精密单点定位中，单系统中GPS的定位精度和收敛时间优于Galileo，双系统组合的定位精度和收敛时间优于单系统，GPS/Galileo组合优于GPS/QZSS组合优于Galileo/QZSS组合，三系统组合的定位精度和收敛时间优于双系统组合。

3）在动态精密单点定位中，单系统中GPS定位精度和收敛时间优于Galileo，双系统组合的定位精度和收敛时间优于单系统，三系统组合的定位精度和收敛时间明显优于双系统组合。