Delaunay三角网生长法的优化与应用

韦云舰，卢 中

（1.甘肃省地质矿产勘查开发局第三地质矿产勘查院，甘肃 兰州 730050；2.中交第二航务工程勘察设计院有限公司，湖北 武汉 430071）

工程测量中常采用不规则三角网（TIN）模型来表示地形。为了使三角形能更好地对地形变化进行拟合，应尽量使三角形接近等边，三角形的最小角最大。经证实，一般情况下在所有可能形成的三角网模型中，Delaunay三角网是最优的。由于Delaunay三角网构网复杂，因此不同算法的执行效率存在较大差异。现有较成熟的Delaunay三角网构网方法主要包括三角网生长法、逐点插入法和分治法3种，各有利弊[1-4]。本文以经典Delaunay三角网生长法为基础，对三角形寻找第三点的方法进行了优化，明显提升了该方法的执行效率；并将三角网成果用于提取道路断面，分析了其实用性。

1 经典Delaunay三角网生长法

Delaunay三角网生长法是基于Delaunay三角网的空圆特性的，即Delaunay三角网中任意一个三角形的外接圆内不存在其他点。基于此， Delaunay三角网生长法的构网步骤为：①任选点库中的一个点P1；②遍历点库，寻找距点P1最近的点P2，并与之相连构成第一边，添加到边库中；③遍历点库，寻找第三点与P1、P2构成三角形，使之外接圆满足空圆特性，并将第三点与P1、P2的连线添加到边库中，相应的三角形添加到三角形库中（如ΔP1P2P4外接圆内存在点P3，不满足条件，而ΔP1P2P3外接圆内不存在其他点，满足条件，如图1所示）；④遍历边库，判断各边两侧是否应构建新的三角形，若边两侧均存在三角形或不存在其他点，则该边已构建完成，否则重复步骤③、步骤④，直至所有边均构建完成，如图2所示，如边P1P2左侧存在ΔP1P2P3、右侧无点，则无需构造新的三角形，该边已构建完成，边P1P3右侧存在ΔP1P2P3、左侧无三角形且仍存在其他点，则应继续寻找第三点构建新的三角形。

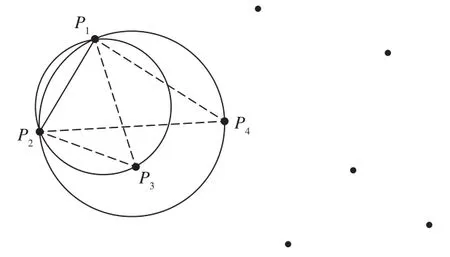
图1 Delaunay三角网构建过程

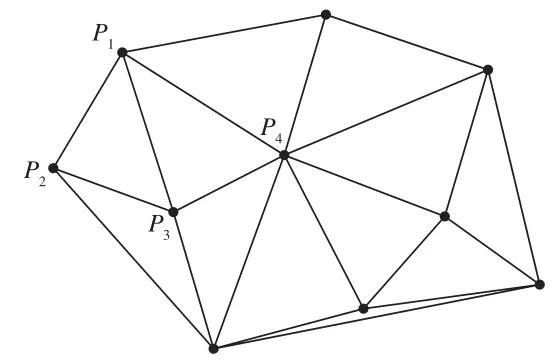
图2 Delaunay三角网构建结果

2 算法优化

由Delaunay三角网的构建过程可知，其耗时操作主要在寻找第三点上，因此算法优化主要用于简化第三点的寻找过程[5-9]。

2.1 排除封闭点

封闭点的概念由贺全兵[10]等提出，在寻找第三点构网的过程中会不断产生封闭点。以P1为起始点经过3次遍历后的结果如图3所示，此时点P3已被三角形所包围，称之为封闭点。封闭点将不再参与下一次遍历边库寻找第三点的过程，因此第4次遍历前可将点P3从备选点库中移除。通过动态地排除封闭点，可将第三点的备选范围不断缩小，以减少寻点时间。

尤磊[11]等在封闭点概念的基础上提出了以优先点为中心的Delaunay三角网构建方法，是对排除封闭点方法的进一步优化。具体方法是对于新增的三角形角点Pi，优先扩展以Pi为角点的边，待Pi成为封闭点后将其从备选点库中移除，此时称Pi为优先点。采用该方法能更快地将优先点变为封闭点，优化备选点库，提高构网效率。

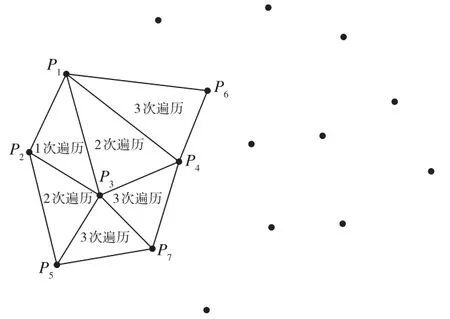
图3 封闭点示意图

2.2 第三点排序

由Delaunay三角网的空圆特性和最大最小角特性可知，第三点大概率会出现在前两点附近（点集边缘的三角形除外）。如图4所示，在进一步寻找P1P6左侧三角形的第三点时，第三点大概率会是距离P1P6中点（设为P1-6）最近的P8、P9、P10之一，而不会是远处的Pn、Pn+1。由于点集中点的顺序是无规律的，每次判断某点是否为第三点时，均需遍历点集中的其他点是否在第三点的外接圆内，极为耗时，因此本文算法在每次寻找第三点时均会根据备选点到前两点的距离进行排序，即最靠近P1P6中点P1-6的点优先进行空圆判断。设点P1、P2、…、Pn坐标依次为（X1,Y1）、（X2,Y2）、…、（Xn,Yn），即P1-6P8长度可表示为：

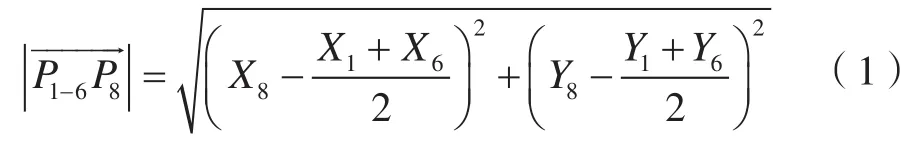
本文采用冒泡排序法选取距离前两点最近的i个点优先进行空圆判断，寻找第三点。由于每次排序均需根据式（1）计算所有备选点到前两点中点的距离，考虑到对于计算机而言，浮点类型数据的加减法执行效率比乘除法高数十倍，因此以式（2）代替式（1），可近似筛选距离最近的点，可大幅提升冒泡排序效率。

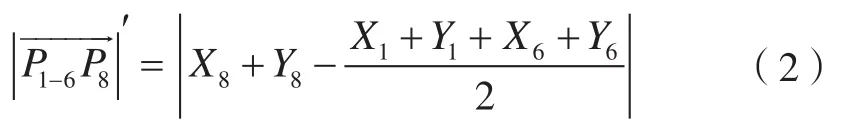
冒泡排序法需重复遍历待排序的数组，依次对比相邻元素，若相邻元素排序错误则交换其顺序，因此选取距离最近的i个点需进行i次遍历。遍历次数越大，即筛选的最近点越多，目标点出现在最近点中的概率越大，但排序耗时也越长，因此需测试选择最佳遍历次数。本文选用10 000个不规则排序的三角网点作为测试数据，测试了遍历次数、最近点包含目标点的概率、构网时间三者的关系，结果如表1所示，可以看出，当筛选的最近点逐渐增多时，最近点包含目标点的概率将迅速增大，但难以达到100%，此时最近点不包含目标点的情况主要出现在三角网边缘的狭长三角形中。以图5为例，在寻找P1P2右侧的Delaunay三角形时，目标点为Pn，而采用排序法优先选取的最近点依次为P3、P4、P5、P6等，这种情况在三角网边缘难以避免，因此遍历次数应以三角网的构网时间为依据，取最佳遍历次数为7。

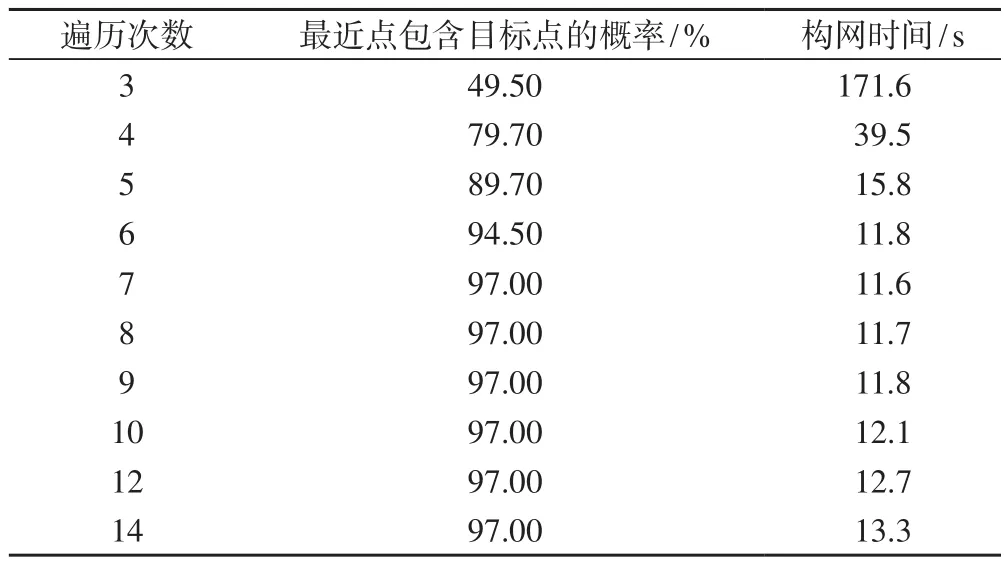
表1 三角网生成时间汇总表（取样点为10 000）

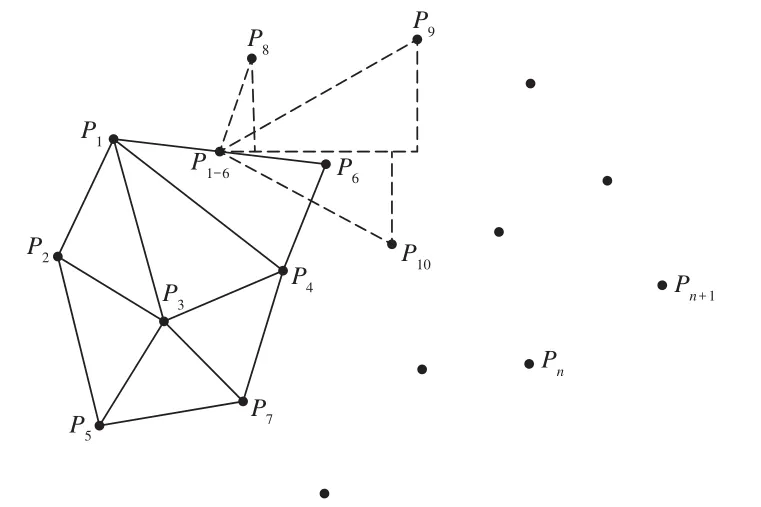
图4 第三点排序方法

图5 三角网边缘构网示意图

2.3 算法执行效率比较

本文采用优化前后的Delaunay三角网生长法对不同数量的样本点进行处理，并对构网时间进行汇总，结果如表2所示，可以看出，优化后的Delaunay三角网生长法的执行效率得到了明显提升，随着样本点数量的增加，效率提升效果将更为明显。程序的执行效率受编程语言、计算机性能、采样点排序等诸多因素影响，本文采用Java语言编写程序，程序运行于Windows10 64位系统中，计算机处理器为Intel Core i5 2.30GHz，内存为8G，采样点为完全随机样本。

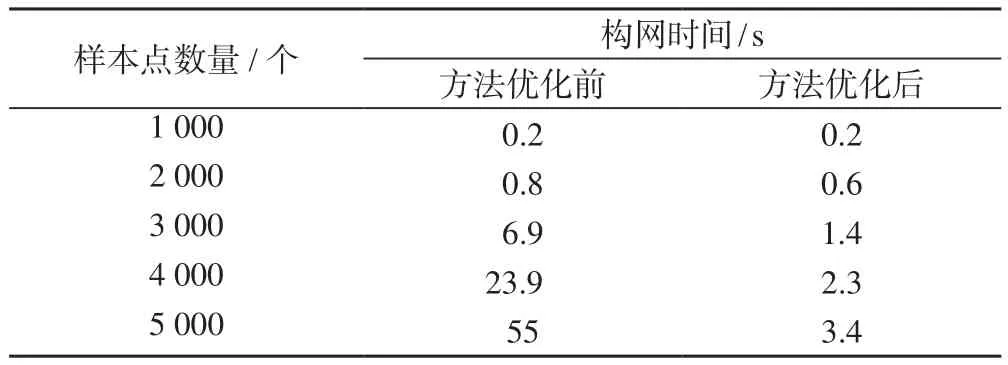
表2 样本数量与构网时间汇总表

3 基于Delaunay三角网的断面提取方法

由地面高程点构成的Delaunay三角网可用于表示地形起伏，当高程点密度足够时，可在三角网的基础上内插指定点位高程。基于此，可在Delaunay三角网的基础上提取道路横断面，具体方法为：①根据设计断面端点坐标和点间距计算断面节点坐标；②根据节点平面坐标判断节点所在三角形；③根据三角形角点三维坐标确定三角形所在平面方程，再代入断面节点平面坐标，计算节点高程。

为了提高程序执行效率，判断节点是否在三角形内时采用向量法。如图6所示，判断断面节点Ti是否在ΔP1P2P3内时，可将向量表示为向量和向量的矢量和，即

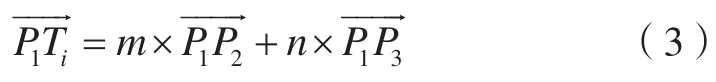
当m、n满足以下3个条件时，可判定节点Ti在ΔP1P2P3内。

设ΔP1P2P3所在平面方程为Z=A×X+B×Y+C，Pi点的三维坐标为(Xi,Yi,Zi)，代入平面方程解得：

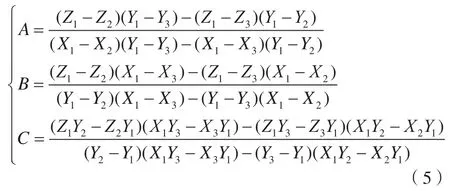
代入节点Ti的平面坐标(XTi,YTi)，得到其高程，则有：

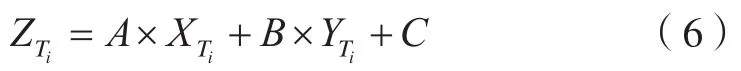
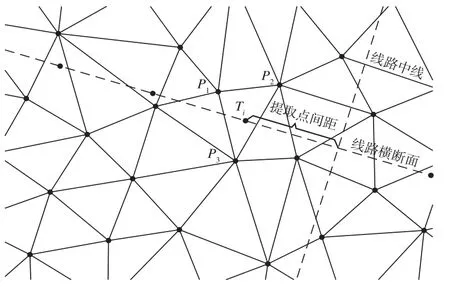
图6 断面提取过程示意图

4 案例分析

本文的实验数据源自上饶至浦城高速公路（江西境内）的新建工程，项目定测外业时间紧、任务重，且存在大面积山区密林地段。定测时正值冬季，树叶相对稀少，利于激光穿透植被，常规测量手段施测困难，因此项目的横断面测量采用机载激光雷达施测。机载激光雷达外业作业平均航高为200m，点云平均密度小于10cm。在测区范围内，选取合适的特征点利用RTK进行检测，结果如表3所示，可以看出，激光雷达数据可靠，可满足断面测量精度需求。

本文采用均值法提取平均点密度为3m的点云用于生成三角网，并提取道路横断面，将提取的横断面成果与实测横断面进行对比，结果如图7所示，可以看出，采用程序提取的横断面成果与实测成果吻合良好，误差主要集中于变坡处，若适当提高横断面节点的提取密度可使变坡处的拟合效果更好。本文提取横断面节点的间距为1m，横断面提取结果与RTK实测结果相比最大较差小于0.2m，可满足精度需求，方法具备可行性。

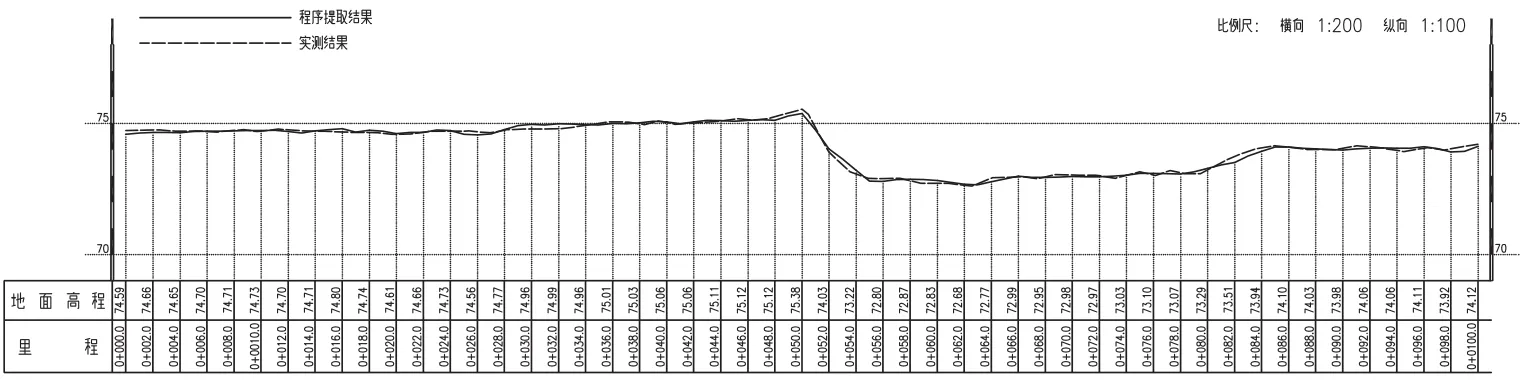
图7 横断面示意图

表3 激光雷达数据检测结果统计表

5 结 语

本文在Delaunay三角网生长法的构网过程中，通过排除封闭点和第三点排序的方法对原有方法进行了优化。经验证，优化后的Delaunay三角网生长法的执行效率得到了明显提升。本文利用优化后的Delaunay三角网生长法将机载激光雷达施测的高密度点云数据生成三角网，并在此基础上对道路横断面数据进行提取，经RTK检测可知，提取的横断面数据成果精度良好，方法具备可行性。