开口加劲板件的稳定极限承载力研究

甘采华, 王 华, 刘世建

(1.广西荔玉高速公路有限公司, 广西 南宁 530022； 2.广西交科集团有限公司, 广西 南宁 530007)

交通是国家的大动脉，桥梁作为交通基础设施的重要结构，随着国民经济的发展，对桥梁建设提出了更高的要求。扁平钢箱梁斜拉桥因其整体性强、线条美观、强度高、自重轻、工厂化程度高、质量可靠程度高、工期短等优点，在大跨度桥梁中得到了广泛应用。扁平钢箱梁由薄钢板组成，为发挥材料的承载能力，常采用高强度材料，但结构因屈曲而丧失承载能力的现象日益突出。已有诸多学者对斜拉桥的整体-局部非线性相关稳定极限承载力进行了研究，孙若晗[1]等以芜湖长江公路二桥为背景，分析了其极限承载力性能及在不同荷载分布时桥梁的破坏路径；王明[2]以主跨780 m的钢箱梁斜拉桥为工程背景，分别分析了悬臂施工阶段和运营阶段结构的稳定性，并对斜拉桥稳定安全系数的合理取值及弹塑性失稳破坏机理进行了研究。梅红蕾[3-4]等对比分析了扁平钢箱梁U型加劲板各国不同规范的稳定承载力计算方法，证实了加劲板件的相对刚度比对结构稳定承载力有着很大的影响；王飞[5]利用钢箱节段U型加劲板件数值模拟及试验验证相结合的方法，针对加劲板的稳定承载力计算分析提出了简化计算模型并进行了验证；赵秋[6-7]等考虑U形肋翼缘与腹板间弯曲半径变化、U形肋腹板宽厚比及被加劲板宽厚比等因素，通过轴压试验得到了U形肋加劲板的稳定极限承载力、局部失稳破坏模式等受力性能参数；并利用四边简支板简化U肋加劲板及其腹板简化，根据数值模拟方法验证了简化模型的正确性；秦凤江[8]等利用有限元法及试验对比验证分析了钢箱梁U型肋加劲板的稳定极限承载力；也研究了焊接残余应力、初始几何缺陷等参数对U型肋加劲板稳定极限承载力的影响规律。赵秋[9]等通过U肋加劲板的塞尺试验结合最小二乘法及统计学方法，对钢桥面板整体和局部几何缺陷的幅值进行了研究；王欣南[10]等利用初始几何缺陷代替残余应力的方法结合有限元计算分析了开口肋加劲板的稳定承载力。

基于上述研究成果，本文将对不同相对宽厚比系数的斜拉桥主梁钢箱开口加劲板件稳定极限承载力展开研究，分析钢结构焊接残余应力及结构制造误差产生的初始缺陷对开口加劲板件稳定承载力的影响。

1 加劲板件的初始变形、残余应力及其本构关系

1.1 加劲板件的初始变形

加劲板件在其制造焊接加工时常会产生初始变形，初始变形的存在会使加劲板件产生附加弯矩，且初始变形越大，附加弯矩便越大，故在进行加劲板件受力性能分析时，须考虑初始变形的影响。影响加劲板件稳定极限承载力的初始变形因素主要有两个：① 整体和局部的幅值；② 整体和局部的形态。对于加劲板件初始变形幅值，本研究拟采用BS5400英国桥梁规范中板件的加工误差限值作为板件局部的初始变形幅值；取板件短边的l/1 000作为板件的整体初始变形幅值。图1为结构局部初始变形幅值计算示意图，具体计算如式(1)所示。

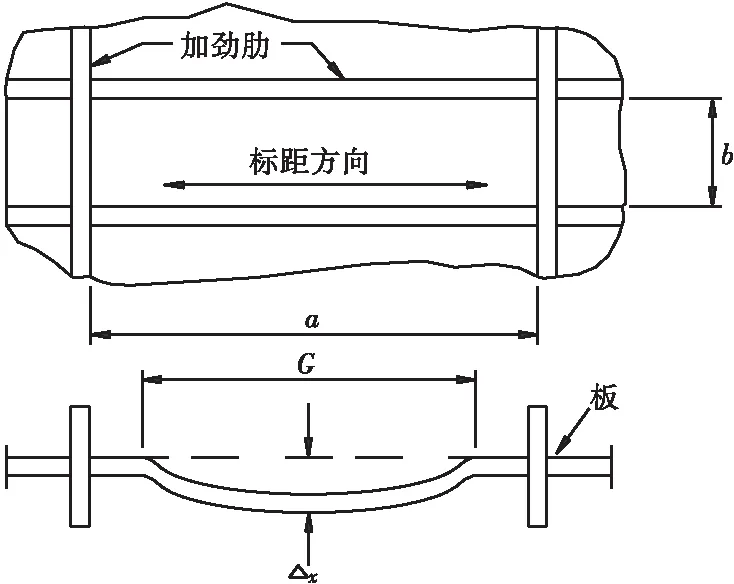
图1 结构局部初始变形幅值计算示意图

(1)

对于初始变形整体和局部形态的问题。在有限元建模时取用单波的模态考虑初始整体变形，采用加劲板件一类稳定的模态按式(1)所计算幅值放大或缩小来考虑加劲板件初始局部变形。

1.2 加劲板件的残余应力

构件的残余应力是构件内部自相平衡的内应力。截面的形状和尺寸、型钢和钢板的轧制、焊接工艺和材料性能等一系列因素均对沿构件轴线方向截面的纵向残余应力分布和大小有影响[11]。

因钢箱梁斜拉桥主梁结构板件数目众多，且自身构造较为复杂，焊接缝密布，导致其残余应力分布规律尚不明确，仅能通过试验测试获得真实的索塔残余应力分布。而对于斜拉桥扁平钢箱梁，目前国内几乎无残余应力相关有效的测试资料。为能通过数值分析的方法研究加劲板件残余应力对其稳定极限承载力的影响规律，本文参考了日本多多罗大桥[12]对于开口加劲肋的一些实测结果。残余应力σrc的峰值采用80 MPa，即0.23σY(屈服强度σY=345 MPa)。

1.3 加劲板件材料的本构关系

多采用Q345钢材作为扁平钢箱梁斜拉桥的主梁材料，学者们通过大量试验资料验证了静力作用下钢材拉、压性能基本一致。为对加劲板件结构弹塑性稳定理论进行研究，现根据诸多相关构件的试验结果及钢材应力应变曲线的特点，将应力应变关系简化为图2所示的3种本构关系。

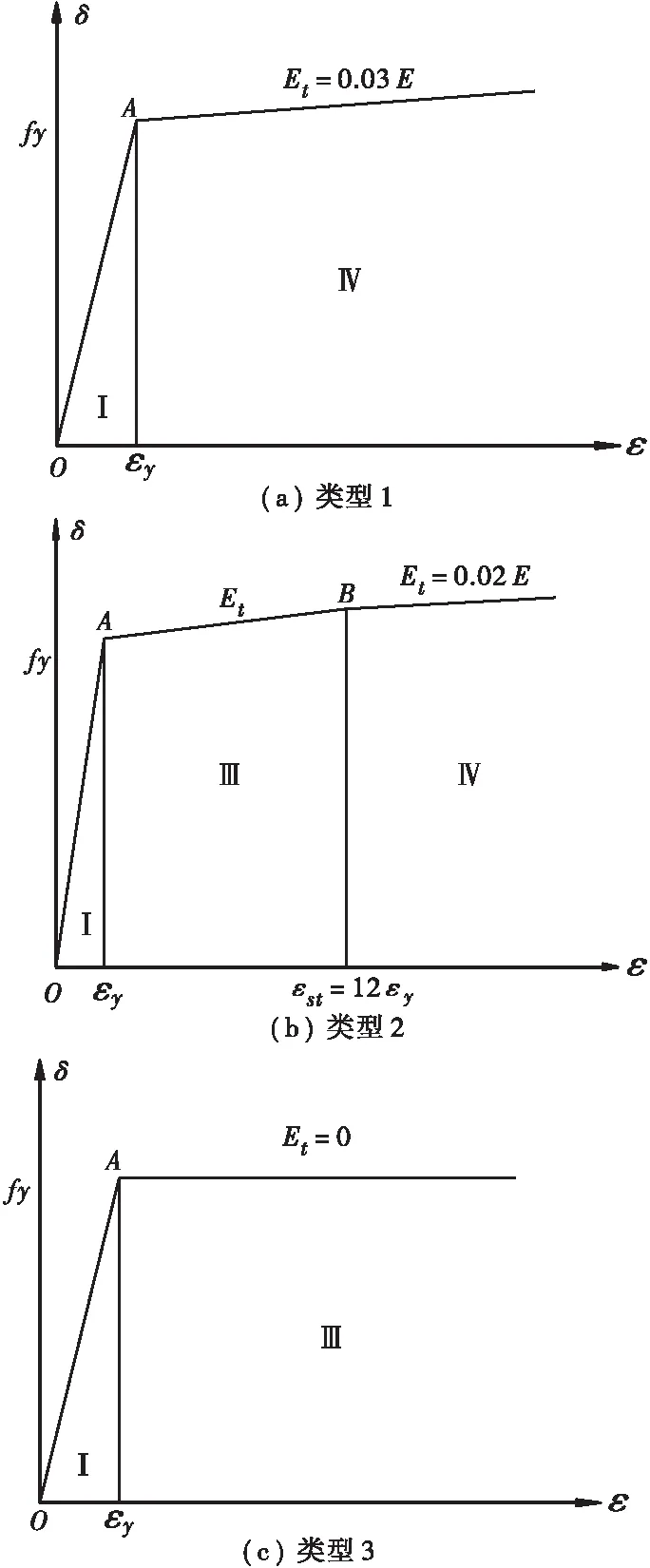
图2 钢材应力应变曲线

钢材达到屈服强度后的应力应变曲线有如图2所示的3种类型：① 类型1如图2(a)所示，其基于钢材连续屈服理论，即当钢材应力达到屈服应力强度后出现连续滑移面，且材料呈弹塑性，其弹性模量Et=0.03E；② 类型2如图2(b)所示，其基于钢材非连续屈服理论，即当钢材应力达到屈服应力强度后发生部分滑移，应变介于εy和εst之间，可取εst=12εy，且当ε≥εst时，可取Est=0.02E；③ 类型3如图2(c)所示，当ε≥εy时，取切线模量为Est=0。诸多研究成果表明[13-14]，采用上述3种不同类型的材料本构关系进行构件极限承载力计算分析时,结果仅有细微差别，且上述类型中第3种类型的计算过程最为简洁，故用第3种类型图示2(c)中的材料本构关系进行研究分析。

2 加劲板件屈曲理论分析

加劲板件屈曲分整体和局部屈曲，加劲板件整体屈曲是指包括板和加劲肋在内的整体结构跟单板一样的屈曲模态；加劲板件局部屈曲是指加劲板件的加劲肋之间局部板件跟单板一样屈曲而加劲肋并不屈曲的模态。本文采用三上市藏、Giencke，E.等[15-16]的分析理论进行结构屈曲分析，加劲板件示意图如图3所示。

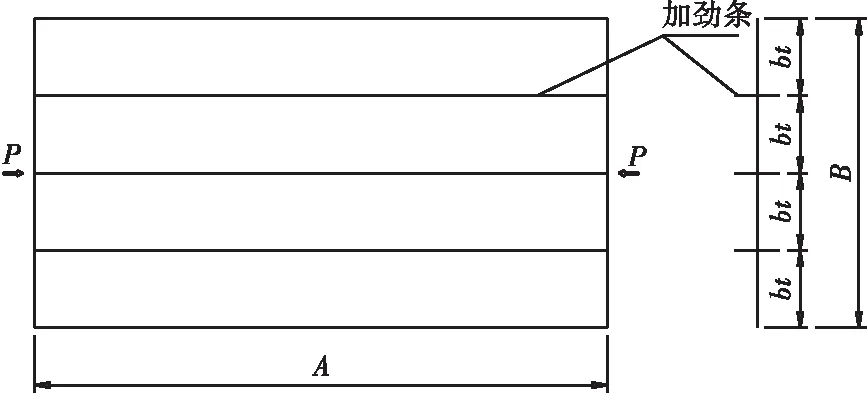
图3 单向受压的加劲板

加劲板的屈曲应力的公式为：

(2)

式中：t*为正交异性板的换算板厚，定义见式(4)；n为板条数；αt=A/B为板的纵横比；αt0的定义见式(6)；γt为加劲板的抗弯刚度比，定义见式(5)。

(3)

(4)

(5)

(6)

n=nt+1

(7)

其中，At，It分别为单根加劲肋的面积和对板中面的抗弯惯性矩；nt为加劲肋数量。

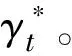
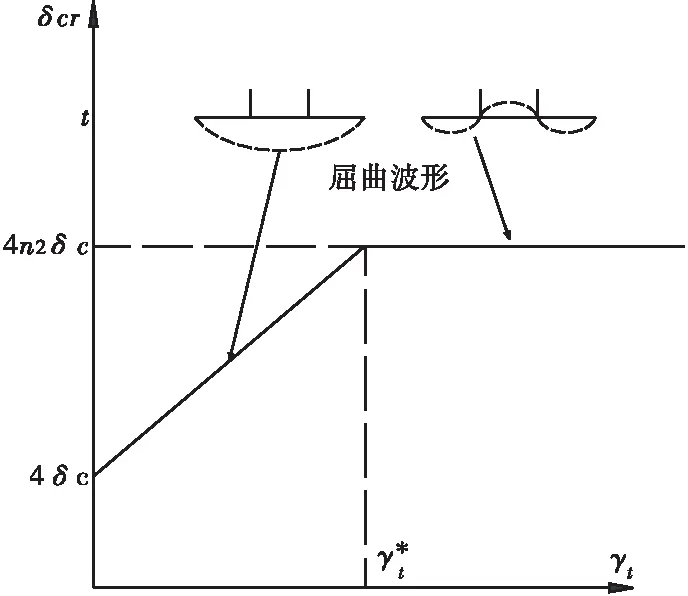
图4 局部屈曲的最小刚度比

计算最小刚度比的公式为：

(8)

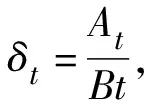
3 有限元模型建立

本文以某独塔双索面钢斜拉桥为研究依托背景，主梁为钢箱梁，梁高5.2 m，材料为16 Mn(Q345)钢，其桥跨布置为(3×72+248+560)m，斜拉索为抗拉强度为1 860 MPa的Φ7钢绞线，全桥共35×2对斜拉索，标准索距为15 m(北岸尾索区索间距为9 m)。钢箱梁顶底板及腹板厚2 cm；加劲板件厚1.6 cm，高16 cm。具体立面布置见图5。

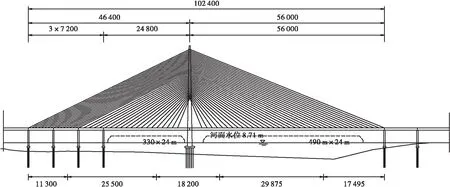
图5 某大跨斜拉桥立面布置(单位：cm)

根据上述工程背景，利用有限元软件ANSYS采用混合单元法建立结构整体模型，其中斜拉索采用索单元link10模拟，并利用Enrst公式考虑弹性模量的修正；主塔使用Solid45三维实体单元模拟，且主塔与扣索之间共节点；主梁采用壳单元shell63和梁单元beam188分别进行模拟，并利用MPC184单元将横梁等效为刚性梁；通过建立位移方程来实现交界面上单个梁单元节点和多个壳单元节点之间的位移协调[13]。具体方程表述如式(10)所示。结构整体模型示意图如图6所示。

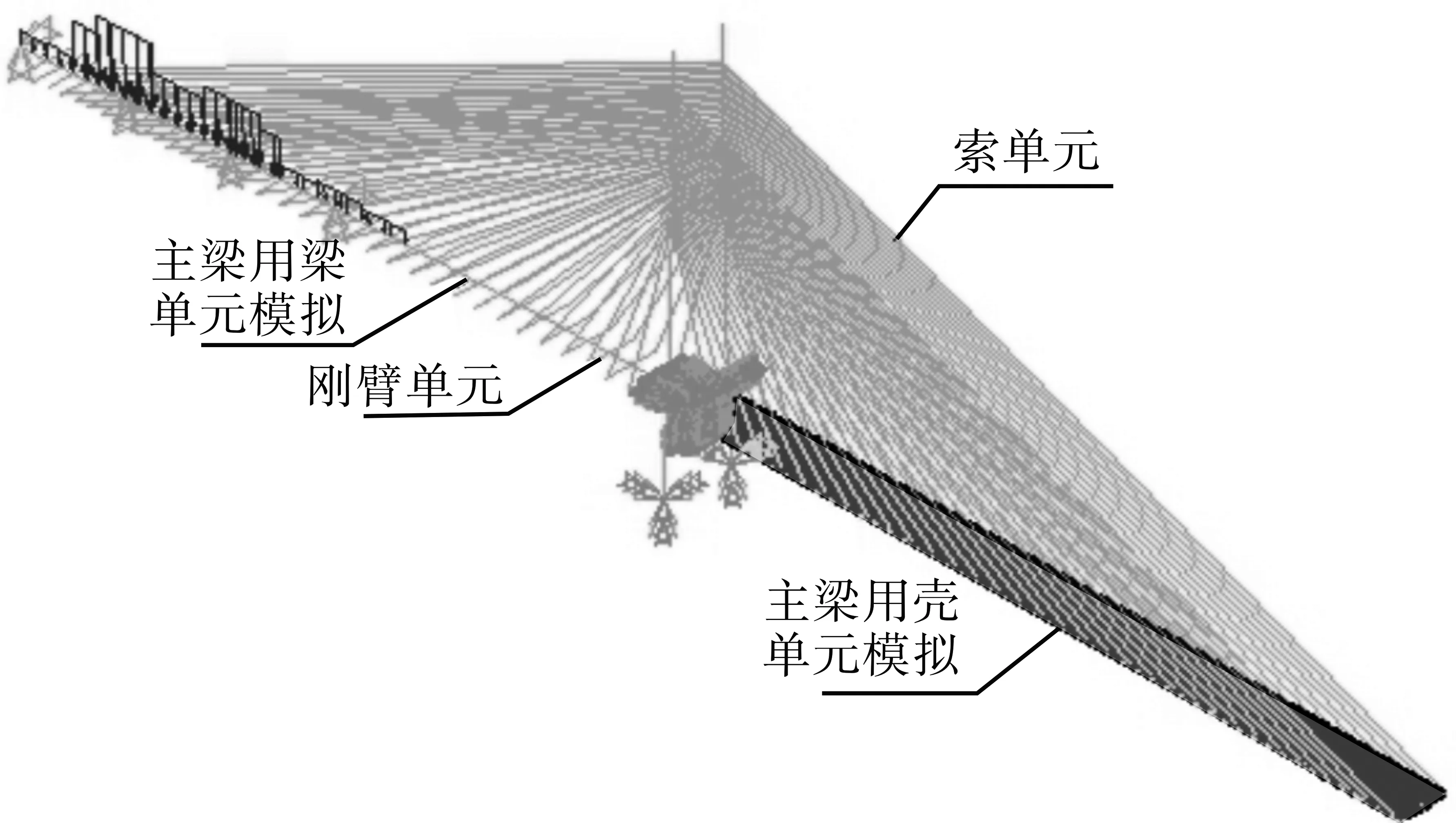
图6 斜拉桥整体混合模型图

Un=Fn(Ubeam)

(10)

式中：Un为交界面上壳单元的任意一个节点的位移，Ubeam为交界面上梁单元节点的位移。n表示交界面上壳单元的节点个数(交界面上壳单元节点个数也对应了位移方程个数)。主梁局部模型图及位移方程的示意见图7。

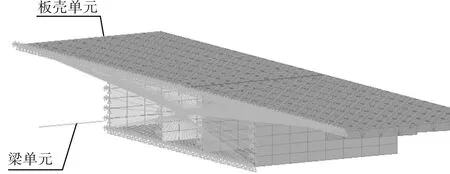
图7 梁单元和板壳单元连接的位移协调示意图

4 开口加劲板件稳定极限承载力分析

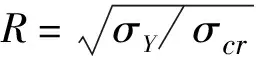
由图8～图10分析有，对比由加劲板件材料屈服强度和欧拉应力(弹性屈曲荷载对应的应力曲线)组成的“上界曲线”，考虑了加劲板件的初始变形及残余应力后的加劲板件稳定极限平均应力曲线有一个下降值Δσ。该下降值Δσ受加劲板件的初始缺陷、残余应力分布和刚度特征等的影响。

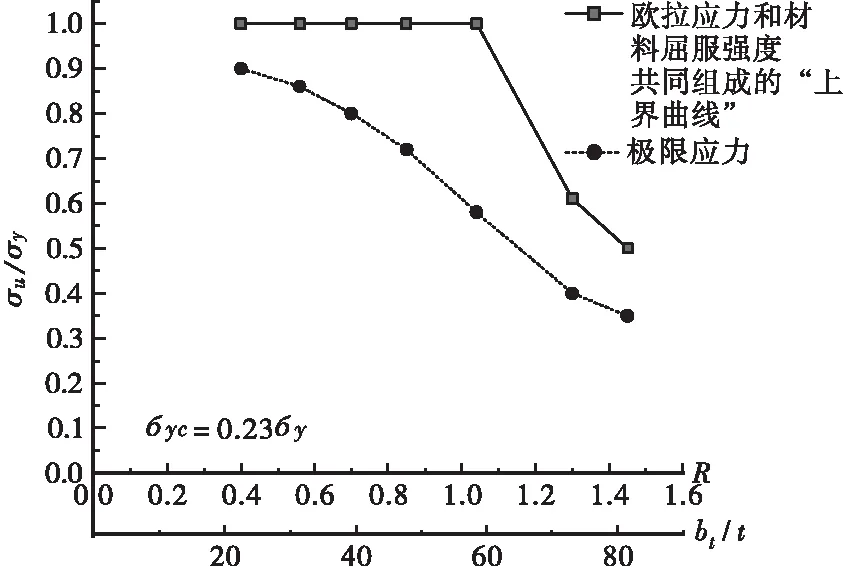
图8 γt=0.5γt，req时的稳定极限承载力曲线

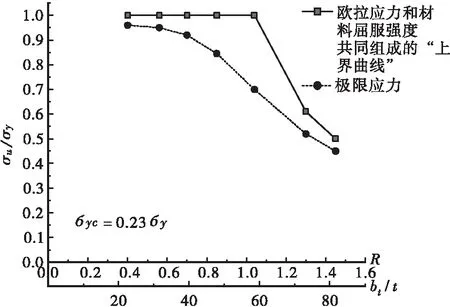
图10 γt=2.0γt，req时的稳定极限承载力曲线

从图9中还可以看出，下降值Δσ在第2点达到最大(为117.3 MPa)，在第1点下降值Δσ为41.4 MPa，在3点Δσ为24.2 MPa。若把初始变形和残余应力均称为缺陷的话，证明R=1，bt/t=55左右的加劲板件的设计对缺陷最为敏感，在设计时应引起注意。下面针对R=1，bt/t=55的加劲板件，分析加劲板件初始变形和残余应力对其稳定承载力的影响效应。

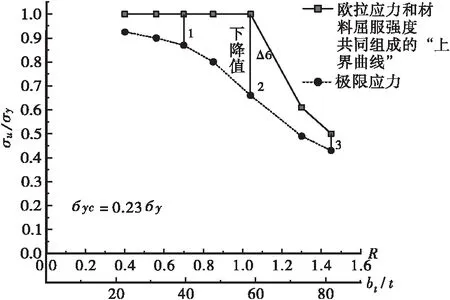
图9 γt=1.0γt，req时的稳定极限承载力曲线

4.1 初始变形的影响分析

为分析初始变形对开口加劲板稳定极限承载力的影响，以γt=1.0γt，req，母板厚度为12 mm，bt/t=55，残余应力σrc=0.23σY的加劲板为例，计算分析了整体初始变形幅值Δ从0到L/1 500到L/500变化时加劲板的稳定极限承载力的变化情况，并将其分析结果总结如图11所示，加劲板的稳定极限承载力随整体初始变形的增大而减小，当整体初始变形幅值Δ从0到L/500时，加劲板的稳定极限承载力的最大差值达24.5%。

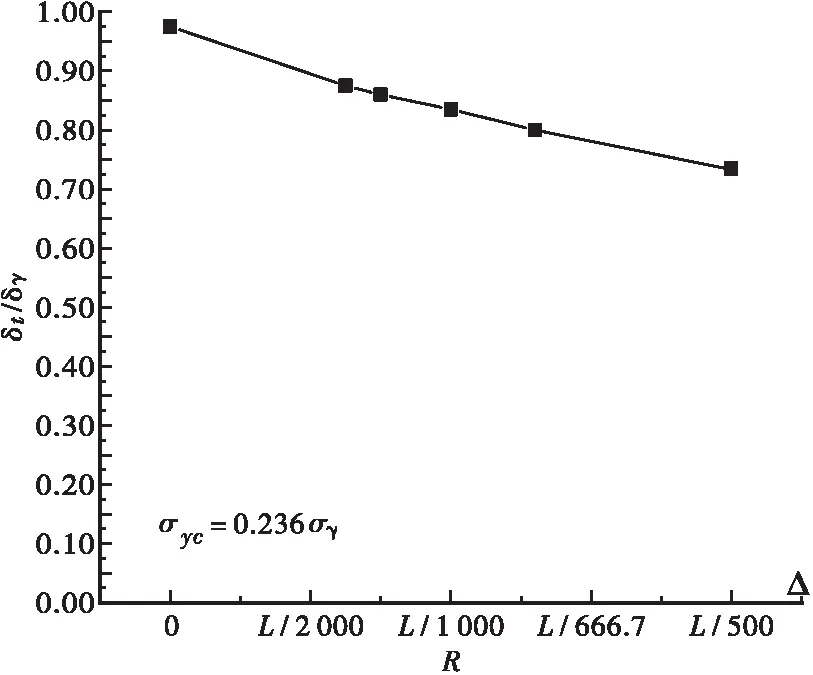
图11 开口加劲板的稳定极限承载力随整体初始变形幅值Δ的变化曲线

4.2 残余应变的影响分析

为研究残余应力对开口加劲板稳定极限承载力的影响，以γt=1.0γt，req，母板厚度为12 mm，bt/t=55，整体初始变形幅值Δ为L/1 000的加劲板为例，计算分析了残余应力σrc从0到σY变化时，加劲板的稳定极限承载力的变化情况，并将其分析结果总结如图12所示，加劲板的稳定极限承载力随残余应力的增加而减小，当残余应力幅值σrc从0到σY时，加劲板的稳定极限承载力的变化最大差值达14.3%。

图12 加劲板的稳定极限承载力随残余应力σrc的变化曲线

5 结论

以某大跨径钢箱梁斜拉桥为研究依托背景，建立了该桥ANSYS混合有限元模型，对开口加劲板件不同相对宽厚比系数下的稳定极限承载力进行了分析，并研究了开口加劲板件初始缺陷及残余应力对其稳定承载力的影响规律，可得到以下结论：

a.当相对宽厚比系数R=1，bt/t=55时，开口加劲板件的设计对缺陷最为敏感，在设计时应引起注意。

b.相对宽厚比系数R=1的开口加劲板件，加劲板件的稳定极限承载力随整体初始变形的增大而减小，当整体初始变形幅值Δ从0到L/1 500到L/500变化时，加劲板的稳定极限承载力的最大差值达24.5%。

c.相对宽厚比系数R=1的开口加劲板件，加劲板件的稳定极限承载力随残余应力的增加而减小，当残余应力幅值σrc从0到σY变化时，加劲板的稳定极限承载力的变化最大差值达14.3%。