基于非线性最小二乘估计的eLoran/INS/磁传感器组合导航方法

闫泓衫，曹 宜，张杨勇，曾歌明，江 鹏

（1.中国人民解放军 92578 部队，北京 100089；2.中国船舶集团有限公司 低频电磁通信技术实验室，武汉市 430205；3.武汉大学 卫星导航定位技术研究中心,武汉 430072）

近年来由于全球卫星导航系统（GNSS）的普及，在现代定位、导航和授时（PNT）体系内GNSS 占据了重要地位，在覆盖范围、精度和使用成本上相对其它导航系统具有明显的综合优势。但由于其脆弱性和易受干扰的缺点，过度依赖GNSS 的PNT 体系在社会的经济安全、生产安全和国防安全方面均存在巨大隐患。因此，世界各国均在寻求建立新一代的PNT 体系。

罗兰导航系统是一种起源于二次世界大战期间的双曲无线导航系统，其有效范围可达2000 km 以上，可穿透一定深度的水体和山体，解决了GNSS 系统无法在室内和水下提供导航的问题，提供了比GNSS 系统更广泛的应用范围。其后续升级的增强型罗兰(eLoran)无线电导航系统普遍被认为是GPS 的最佳代替[1]。英国在欧洲西北部通过布设差分站，建立了eLoran 导航系统[1]并通过测试得出该系统的定位精度最高可达5 m，授时精度可达几个ns[3]，为了应对GPS干扰，韩国也计划建设高精度的罗兰导航系统[4],[5]。

罗兰导航系统的误差主要来源于传播路径上各种因素导致的到达时间（TOA）的延迟误差，可分为时变延迟和空间延迟两大类，其主要成因是由于传播路径上电导率的瞬时变化（ASF 时变）和空间变化（ASF空间）导致的二次附加因子（ASF）的变动，如式(1)所示，若不进行校准，这些误差可导致罗兰接收机解算的位置与实际地点偏离达到数公里。

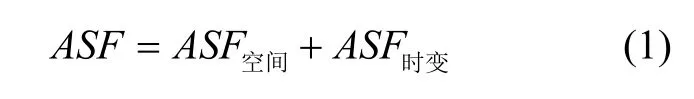
因此，为保证罗兰导航系统的精度，必须设法修正这些误差。其中，空间因素导致的传播延迟可以通过构造ASF 地图[6]来校准，缓慢变化的时变误差可以通过建设差分站（differential station）来实现抑制，但由于受限于罗兰数据通道的速率仅40 bps，对于站点的ASF 更新速度往往有一定的滞后性，故在实际使用中由于远处的雷电等大气噪声或其它随机瞬时因素导致的快速变化的噪声需要通过其它方法抑制。

在导航领域，组合导航通常通过融合几种不同类型的传感器来实现，这些传感器通常具有完全不同的特性，通过传感器相互之间取长补短实现导航精度的提升。在以往的研究中[7]，大多数组合导航系统通常采用GNSS 系统与其它导航方式实现，因此，在建立独立于GNSS 的PNT 系统的目标指引下，新的更加泛在、智能、融合的不依赖GNSS 的组合导航系统在理论和实践中都具有重要意义。

1 eLoran/INS/磁传感器组合导航系统算法基本原理

传统的多传感器信息融合导航算法通常采用卡尔曼滤波算法及其各种改进方法，该方法利用预测-测量模型可以有效融合不同传感器的信息从而提高系统的准确度和适应性，但这些算法在传感器数量较多时，运算量大、占用资源多，不利于设备的低功耗与小型化。因此，针对这个问题Madgwick 等人[8],[9]提出了基于梯度下降算法的组合姿态估计算法，该方法具有运算量小，占用资源少，解算精度高的特点。该算法本质上是利用非线性最小二乘法寻找预测姿态与传感器测量姿态之间残差最小的解，但由于简单的梯度下降算法收敛慢，导致初始姿态对准慢，快速运动时误差增大的问题。因此，采用收敛速度更高的高斯-牛顿算法，可以在保持梯度下降算法优点的前提下提高系统在各种环境下的适应能力。

本文采用eLoran/INS/磁传感器三个分系统组成整个导航系统，其中 eLoran 系统可以提供位置，其差分信息还可以提供地理坐标系中航向φ和速度信息；INS 系统可以提供载体坐标系中角速度和加速度信息，下标s代表载体坐标系；磁传感器可提供载体坐标系内测量到的磁场的信息。

本文所述算法的主要原理是，利用多个传感器对载体的姿态、位置或与它们相关的物理量进行测量，由于各个传感器存在噪声和误差，因此，在实际状况下，载体的姿态和最可能的位置，可以认为是那个使得传感器测量到的物理量与利用载体姿态反推的物理量之间误差最小的非线性最小二乘解。

首先，利用陀螺仪测量载体坐标系中载体旋转的角速度。由于直接利用该角速度计算的姿态角随时间发散，因此，需要增加其它参考矢量来克服此问题。故利用加速度计测量在载体坐标系内的重力矢量，该方位对应于载体的横滚角和俯仰角，再利用磁传感器测量地磁场在载体坐标系内的方位，该方位对应于载体的航向角，由这两个传感器的测量结果与传感器当前估计姿态反推的重力矢量与磁场矢量之间的最小二乘解，计算出姿态角的修正量，这样就可以克服姿态角发散的问题。同时磁传感器和加速度传感器噪声较大，因此反过来也需要利用陀螺仪数据与它们融合，可以有效降低这两个传感器的噪声对姿态角的影响，有效提高姿态角解算精度。

然后，利用载体当前姿态和重力矢量，分离加速度计中运动产生的附加加速度，并对该加速度进行积分，得到在载体坐标系内速度的改变量。根据载体当前速度和姿态，可以得到载体位置的改变量。但是由于加速度计的噪声、计算误差等原因导致的速度误差会随时间累积，这导致位置的误差会随时间发散，因此，需要通过eLoran 导航系统提供的位置和估计的位置之间的最小二乘解，来对计算得到的速度和位置进行修正。

最后，为了提高组合导航系统的实时解算的精度，需要计算速度和角速度的零偏误差，因为该误差既产生长期的累积误差，又会对单次计算产生影响。由于惯性器件的特性，该误差相比高频噪声，是随机且缓慢变化的低频误差，在计算中表现为姿态和位置修正量的低频分量，因此，通过对修正量进行低通滤波可以得到速度和角速度的零偏。

2 导航算法与数学推导

首先，定义载体在时刻t的状态矢量为，位置矢量，姿态四元数，可表示为位置矢量和姿态四元数的函数：

式中，下标ω代表该估计量来自于陀螺仪的输出。再利用加速度传感器数据计算的速度可以得到位置的估计量：

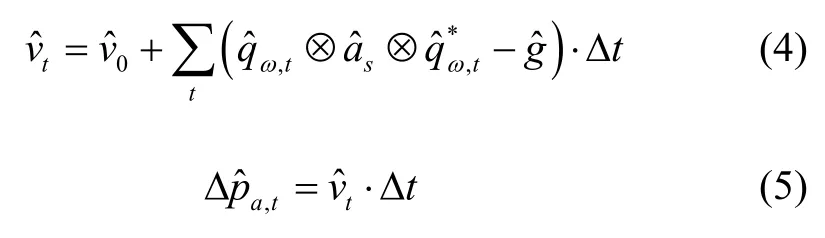
式中，下标a代表该量来自于加速度计的输出，载体状态的增量和估计量分别为：

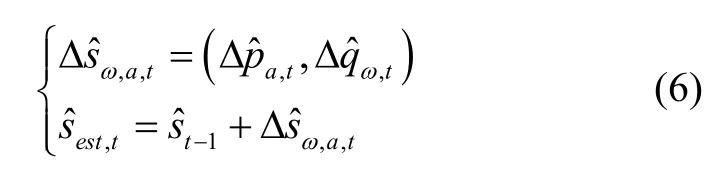
注意，式中由于eLoran 系统通常不提供高度信息，因此，位置的增量需要将高度方向上的数值置零，与四元数进行运算时需要将该矢量填充为四维矢量，在式(6)计算完成后将第一项和第四项，置零并去掉，即可得到：速度的增量也需要用相同的方法进行处理。

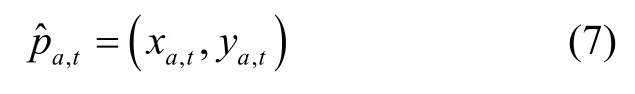
其雅克比行列式为：

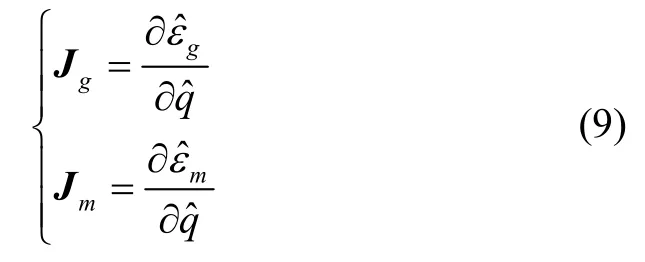
其雅克比行列式为：

整体的误差函数可以构造为：

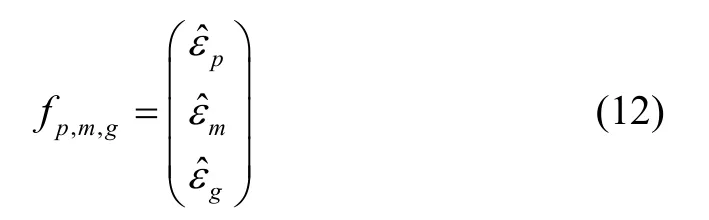
其雅克比行列式为：

根据文献[8]，基于高斯-牛顿法计算这个误差的最小二乘解的载体状态ˆs递推公式中的递推量为：

式中，下标n代表归一化，完整的递推公式为：

其中，μ是收敛步长因子，该参数需要根据传感器的性能进行调整[8]。

在实际情况中，磁传感器和INS 器件都存在误差。磁传感器的软磁和硬磁误差可通过文献[10]中提到的方法进行校准。首先，通过测量各个方向上的磁场，如图1所示的三维球面是一组在载体上的磁传感器实测的结果。然后，利用式(17)中磁传感器误差模型，求解软磁和硬磁校准参数的最小二乘解来校准磁传感器：

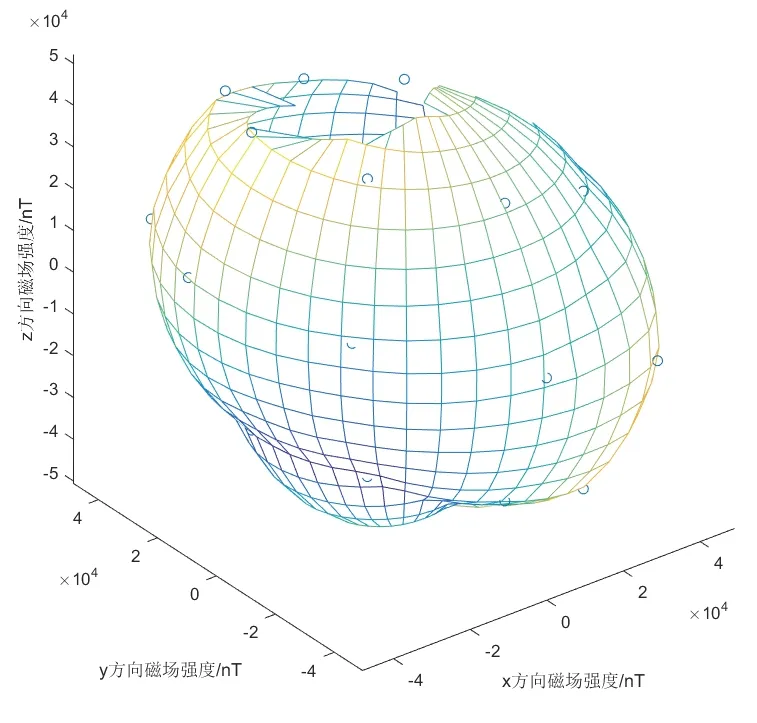
图1 磁传感器原始三维数据Fig.1 Raw 3D data of magnetic sensor

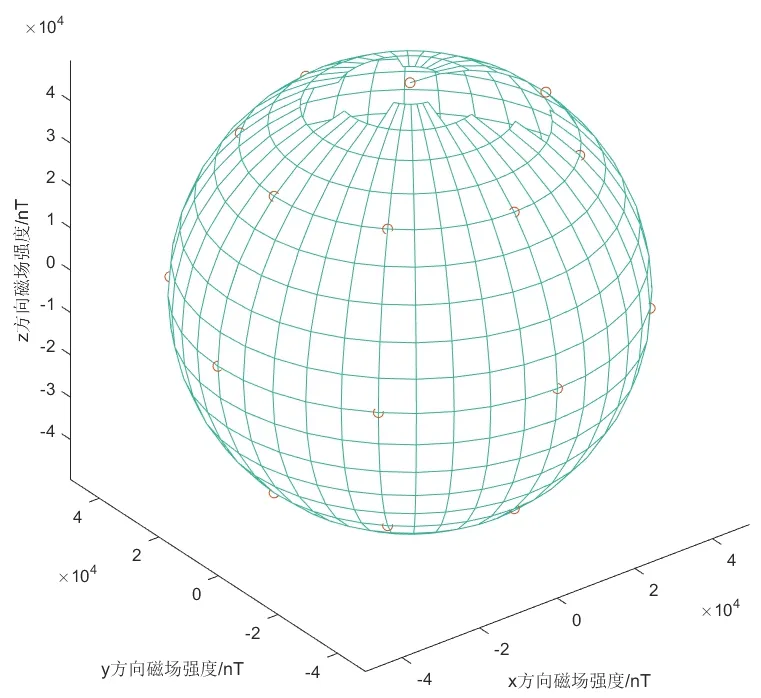
图2 校准后磁传感器三维数据Fig.2 3D data of magnetic sensor after calibration

加速度计和陀螺仪的对载体状态的计算结果存在累积误差，因此，需要通过位置和姿态数据进行补偿，由于陀螺仪的零偏误差为一个缓变量，因此可以通过对估计姿态与测量姿态之间的误差低通滤波得到：

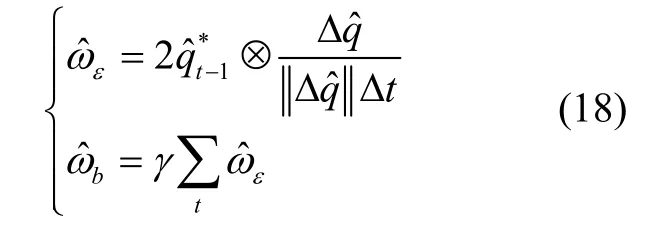
同理，速度的偏置在计算中体现为对位置估计的一个缓变的误差量，可以利用估计位置与eLoran 导航系统给出的位置之差，即式(15)中位置的修正量，再除以时间间隔，并进行低通滤波得到，式(19)中为载体坐标系中速度的修正量，为陀螺仪零偏，δ为常数，控制低通滤波器的带宽。

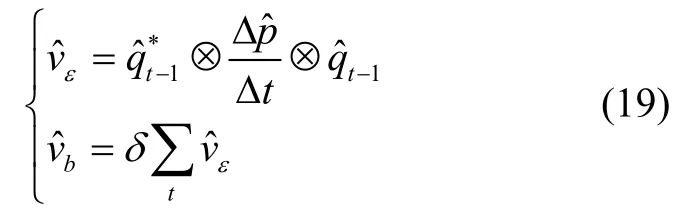
因此，校准后的角速度和速度分别为：

综上所述，该算法完整的流程图如图3所示。

图3 基于非线性最小二乘估计的组合导航算法流程图Fig.3 Flow chart of integrated navigation algorithm based on nonlinear least squares estimation

3 仿真试验结果及分析

为验证上述算法，我们采用了文献[1]所提供的eLoran 误差模型，为了更贴合实际使用情况，选择距离eLoran 台站较远的区域，环境中随机干扰较大，定位误差达到100 m（2σ），远大于GNSS 系统的定位精度。

INS模块仿真采用了湖北三江红峰公司的HZ-1 型光纤惯性测量系统的参数，产品指标如表1所示。磁传感器采用PNI 公司的RM3100 三轴磁场传感器，其噪声RMS 大小为15 nT。

表1 HZ-1 光纤惯性测量产品指标Tab.1 HZ-1 Optical Fiber Inertial Measurement Index

仿真的航线为在海平面内的大角度机动和直线行驶的组合，如图4所示，所有仿真数据均基于该航行轨迹，再结合传感器噪声模型得到，仿真的载体状态的初始值的位置和姿态误差为：偏东100 m，偏北100 m，航向角偏北45 °。图中红色的曲线为仿真航线，绿色的圆点代表eLoran 导航定位数据，橙色的曲线为组合导航系统输出的航行曲线，黑色曲线为惯性导航的输出结果。

图4 仿真航线、eLoran 导航定位与组合导航结果对比Fig.4 Comparison of simulation route,eLoran navigation and positioning and integrated navigation results

可见组合导航系统相对单纯的eLoran 导航系统与仿真航线重合度高，相对惯性导航其误差不随时间发散，可以在连续机动的条件下保持定位精度。其误差分布如图5所示，其定位误差（2 σ）从eLoran 的100 m降低至6.1 m。

图5 eLoran/INS/磁传感器组合导航定位误差与eLoran 定位误差对比Fig.5 Comparison of eLoran/INS/magnetic sensor integrated navigation positioning error and eLoran positioning error

根据式(18)(19)估计的角速度和速度零点偏移的补偿值曲线与实际零点偏移曲线的对比如图6所示。对二维平面运动影响最大的Z 轴角速度的零点偏移的补偿值曲线与陀螺零点偏移曲线如图7所示，从图中可以看出，本算法可以有效地补偿由于惯性器件的特性导致的角度和速度的零点偏移，从而提高组合导航系统的定位精度。

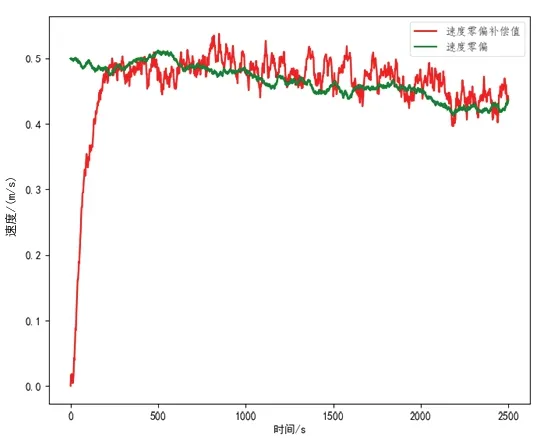
图6 速度零偏曲线和速度零偏补偿曲线对比Fig.6 Comparison of velocity offset curve and velocity offset compensation curve

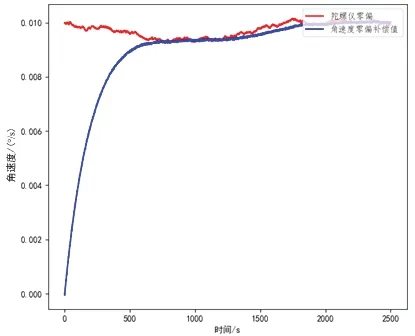
图7 陀螺仪输出z 轴零偏曲线和z 轴角速度零偏补偿曲线对比Fig.7 Comparison of gyroscope's z-bias curve and z-angular velocity compensation curve

4 结论

基于非线性最小二乘估计的eLoran/INS/磁传感器组合导航与单独的eLoran 导航定位相比，通过多种传感器数据融合，提高了信息的冗余度，通过陀螺仪、加速度计和磁传感器给出的姿态和速度信息对当前位置的变化量做出估计，由于INS/磁传感器系统短时的稳定性好，因而可以有效抑制eLoran 导航系统由于噪声干扰导致的定位误差，证明了eLoran 导航定位系统在与INS/磁传感器进行组合后可在eLoran 导航系统有效的作用范围内代替GNSS 定位系统成为可靠的高精度导航定位手段，其穿透力强，可在水下、掩体内、密林中使用，不易受人为蓄意干扰的特点，使其对我国军事和社会经济领域均具备重要的现实意义。