一种船舶漂浮状态下捷联惯导快速自对准方法
刘瑞鑫,刘付成,陈绍红,李传江
(1.哈尔滨工业大学,哈尔滨 150001;2.上海航天技术研究院,上海 201109;3.上海新跃联汇电子科技有限公司,上海 200233)
随着捷联惯导系统在船舶上的广泛应用,船用捷联系统的初始对准对船舶的机动性起着重要的作用。对于初始对准问题,不仅要求对准达到一定的精度,还要求其具有快速性。一般的初始对准的收敛主要是方位失准角的收敛,在粗对准阶段或者精对准阶段采用优化的算法加快方位失准角的收敛。传统的粗对准方案是利用重力和地球自转角速度在地理坐标系和载体坐标系下的投影不同推算出来的。文献[1]提出了新的粗对准算法——凝固对准法,即通过观测不同时刻重力加速度在不同坐标系中的积分矢量计算初始姿态矩阵。近年来以凝固对准法为基础,不断出现了新的变种。文献[2]阐述了凝固对准法通过引入外部速度,如:里程计速度、DVL 速度、GNSS 速度等辅助,可以大大提高动基座粗对准精度。文献[3][4]结合回溯算法通过多级凝固法进行动基座粗对准,提高了粗对准精度。文献[5]将Wahba 问题以QUEST 算法实现,充分利用了粗对准时间段内所有时刻的重力积分矢量。在精对准阶段,一般建立小方位失准角误差模型,采用罗经法或者卡尔曼滤波方法。罗经法,通过合理设置时变控制参数,在精对准初期采取较大的闭环系统振荡频率加速失准角收敛,在对准后期逐渐切换到较小的振荡频率提高对准精度[6]。在理想的惯性器件和稳定的外部环境条件下,卡尔曼滤波有着最优的对准性能。但惯性器件不可避免地受到外界各种环境因素影响,导致系统参数不稳定,从而大大影响滤波性能。文献[7-10]针对建模和外部运动环境的不确定性,在卡尔曼滤波的基础上进行了自适应的改进,以提高系统的鲁棒性。随着计算机技术的发展,导航计算机的性能大幅提升,逐渐产生了重复利用已经存储的传感器数据的回溯导航算法,大大缩短了对准时间[2][11]。上述方法存在如下问题:采用凝固对准法进行粗对准,在动基座情况下如果没有外部速度辅助,精度大大下降从而影响精对准性能;采用非线性大失准角的UKF及其自适应类的变种,工程实践难度增大;同样的,回溯导航算法需要存储大量传感器数据,工程实践难度也大大增加。
与凝固对准法粗对准加卡尔曼滤波精对准的方案不同,本文通过建立非线性的大方位失准角模型,直接采用双通道时变参数的罗经法进行粗对准,在快速达到一定的稳态阶段,失准角已经减小到较小的程度,切换到标准线性卡尔曼滤波精对准状态,通过提高罗经法对准的精度,间接缩短标准卡尔曼滤波精对准的时间。本文最后通过一段船舶漂浮数据进行仿真,表明该方案的有效性。
1 大方位失准角误差模型与控制回路对准
经典控制回路水平对准收敛较快,这里不再阐述,后面的分析均建立在水平姿态失准角为小角度这一条件下。由于初始方位角未知,因此有必要建立大方位失准角误差模型[2],如下
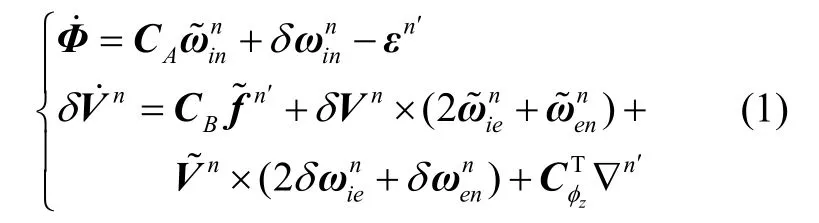
其中,
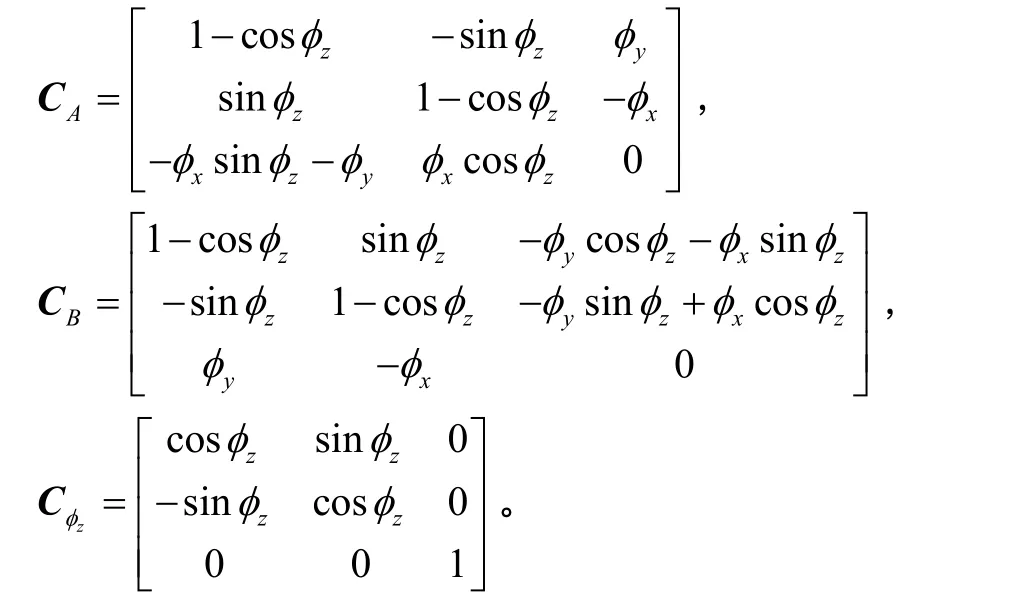
φ为姿态失准角,δV为速度误差,下标和上标中的i、e、n、n′分别表示惯性坐标系、地球坐标系、导航坐标系、计算导航坐标系,表示测量比力,分别表示测量导航系相对惯性系的角速度、测量地球自转角速度、测量导航系相对地球坐标系的角速度,分别表示三者偏差,ε、∇分别表示陀螺和加速度计零偏。
考虑在船舶漂浮状态下载体加速度可近似为0,展开式(1)并忽略天向速度与高阶分量,得误差方程:
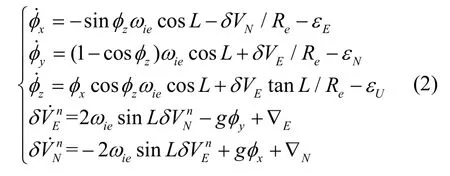
其中,L为纬度,为地球半径,东向干扰加速度和北向干扰加速度分别包含在东向加速度计零偏和和北向加速度计零偏中。
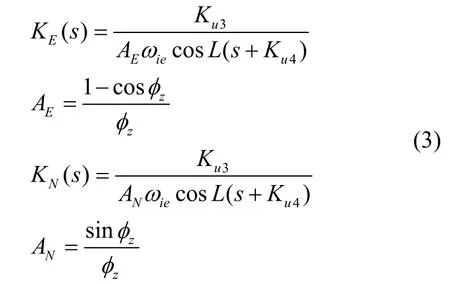
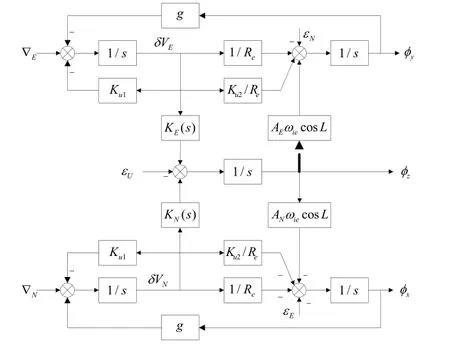
图1 方位对准控制回路Fig.1 Azimuth alignment control loop
由图1 中控制回路可列出控制回路方程
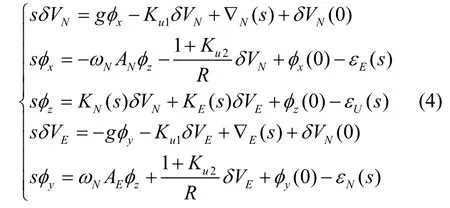

其中0()sΔ为特征多项式
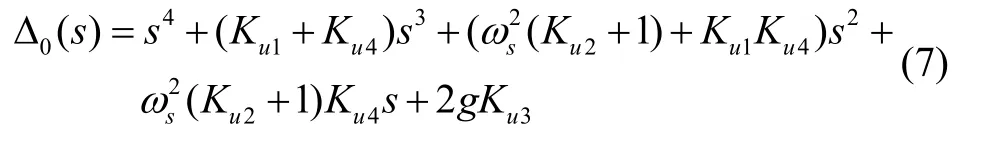
初始方位失准角未知,应按照大值进行评估,水平对准结束后水平姿态角和水平速度误差的影响相对于大方位失准角可忽略不计。由于初始方位失准角未知,和未知,是的函数,分别采用常值和代替,这样式(5)应增加相关的误差项,忽略式(5)中与水平失准角、水平速度误差和零偏项,式(5)变为
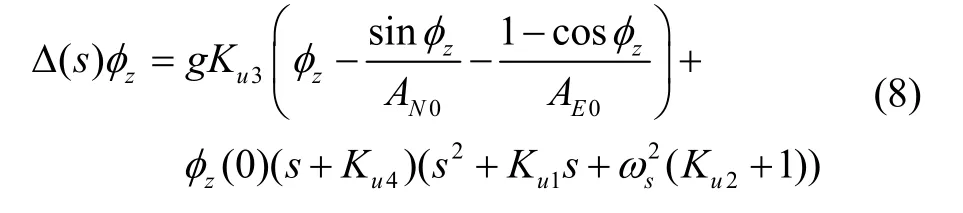
其中

其中()sΔ 为特征多项式。式(8)中等式右边第二项为初始方位失准角引起的响应,随着时间的推移逐渐衰减;第一项由和的取值偏差造成的的收敛过程主要取决于特征多项式中的大小,这一项只影响幅值超调,当逐渐收敛,接近1,接近0,即东向通道作用逐渐消失,此时可断开东向通道的计算,图1 中的虚线代表的是东向通道的断开。方便起见,在对准初期取
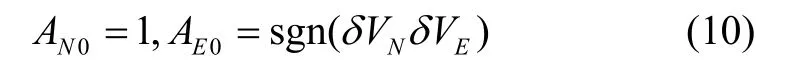
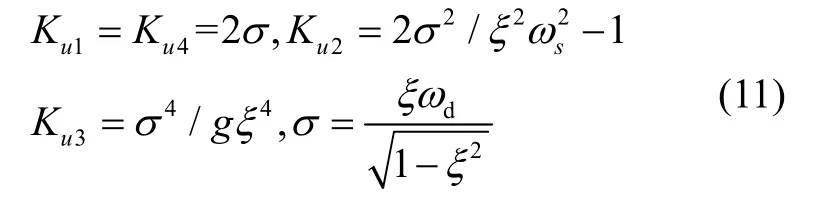

既保证在对准初期快速收敛,又保证在对准末期的方位失准角振荡幅度不至于过大。方位对准结束时刻由dminω确定,这里直接引用文献[7]对罗经法收敛时间分析的结论:对于较大的方位失准角,经过约1.4个阻尼振荡周期就能达到稳态精度。
2 捷联惯导误差模型与卡尔曼滤波
第1 节中的控制回路对准方法能快速使方位失准角收敛,但未考虑到加速度计和陀螺零偏以及漂浮状态下微小的晃动速度与角速度,对准精度不够,本文考虑在方位角收敛到小范围之后进入卡尔曼滤波精对准状态。
对于系统离散方程
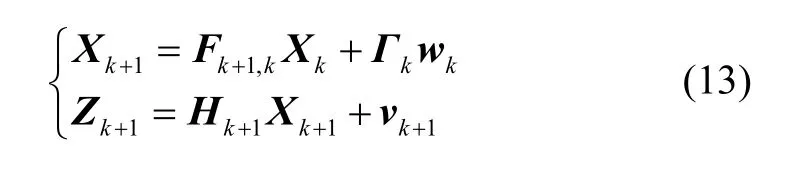

捷联惯导误差模型如下:
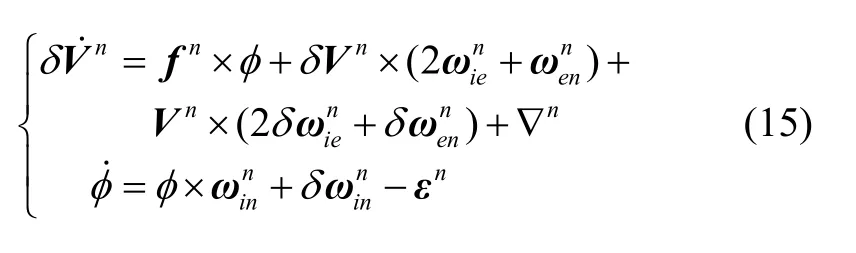
取状态变量
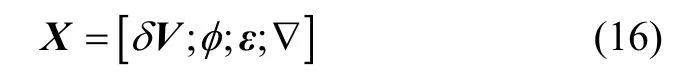
其中∇包含加速度计本身的零偏和漂浮状态下引起的等效随机加速度零偏。
误差方程写成状态方程的形式:

其中w为系统过程噪声。对晃动基座,以速度误差为观测量,则观测方程为:

其中v为测量噪声,观测量。状态初值和状态协方差矩阵初值可根据具体的惯导精度进行设置,一般采用相对较大的初值。
3 对准方案与仿真验证
整个对准方案如图2所示。其中水平回路对准持续20 s,快参数对准持续10 s,变参数方位对准和慢参数方位对准时间由快参数振动频率、慢参数振动频率和变化速率确定。经过约1.4 个慢参数振动周期,方位对准结束,进入卡尔曼滤波精对准状态。

图2 对准方案Fig.2 The plan of alignment
这里采用某型陀螺零偏稳定性为0.01 °/h、加速度计零偏为5 ×10-5g的船用光纤惯组在水上漂浮试验的一段数据进行仿真。试验地点位于 N 43.7127 ° E 126.6952 °,漂浮试验过程中风速约0.3 m/s,GNSS漂浮轨迹如图3,图中“×”表示对准起点,“°”表示对准结束时刻。
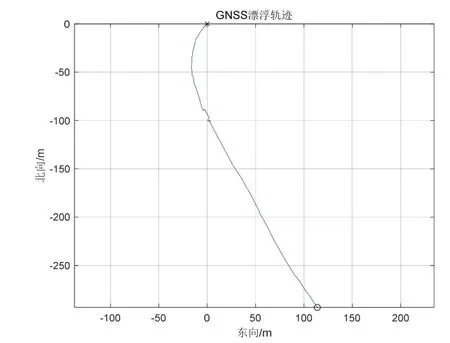
图3 光纤惯导水上漂浮轨迹图Fig.3 The drifting trace picture of optical fiber inertial navigation system
试验初始姿态角均为0 °,进行了三组仿真试验。
仿真一:0~300 s 时间段进行基于重力加速度的凝固对准法粗对准,300 s~900 s 时间段进行卡尔曼滤波精对准。仿真一采用的方法与实际测试方案一致,该试验用作参考。
仿真二:300 s~ 600 s 时间段进行凝固对准法粗对准,600 s~900 s 时间段进行卡尔曼滤波精对准。该试验用作对比。
仿真三:300 s~Ts 时间段采用罗经法对准,Ts~900 s 时间段进行卡尔曼滤波精对准(时间T由罗经对准参数确定)。该试验用于验证本方案。
其中仿真三的罗经对准参数取值为
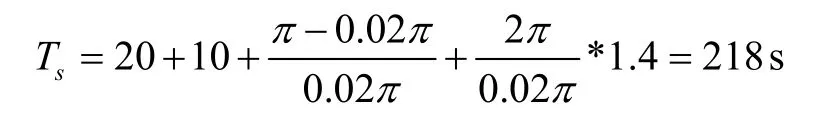
仿真对准姿态角如图4~6所示。图中体现的是300 s~900 s 时间段对准姿态角曲线。其中蓝色虚线、绿色点划线、红色实线分别表示仿真一、仿真二、仿真三的对准姿态角曲线图。仿真一中事先进行了300 s粗对准,随着卡尔曼滤波的进行,姿态角逐渐接近真值,因此后面两组仿真越接近仿真一的结果越能体现方案的对准精度。
由图4 和图5 以及其中的放大图可看出,本对准方案中水平姿态角很快接近仿真一的对准结果,且随着对准的进行最后三组仿真水平姿态角基本重合,这里不再列举具体数值。
由图6 可看出,本方案中的方位失准角由一个大值快速收敛,在160 s 以后方位角相对于仿真一方位角偏差在1 °以内。表1 统计了不同时刻仿真二和仿真三相对于仿真一的方位角偏差。在仿真二粗对准结束时刻,仿真三的方位角偏差比仿真二小一个数量级。之后仿真二和仿真三均进入卡尔曼滤波精对准状态。随着卡尔曼滤波的进行,仿真二和仿真三逐渐接近仿真一的方位角,在仿真结束时刻仿真三的方位角仍比仿真二小。
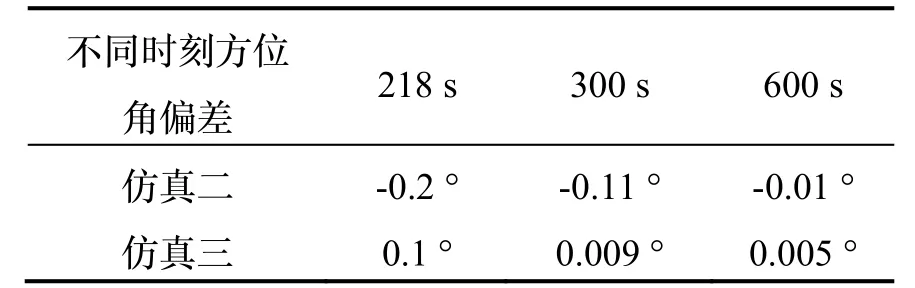
表1 不同时刻方位角对比Tab1.Comparison of azimuth at different times
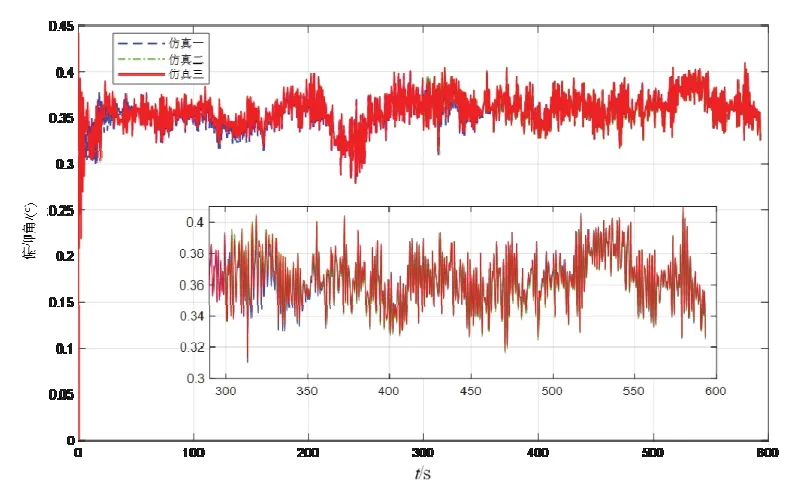
图4 对准过程俯仰角曲线图及部分放大图Fig.4 The pitch angle curve and partial enlarged drawing during alignment

图5 对准过程滚动角曲线图及部分放大图Fig.5 The roll angle curve and partial enlarged drawing during alignment
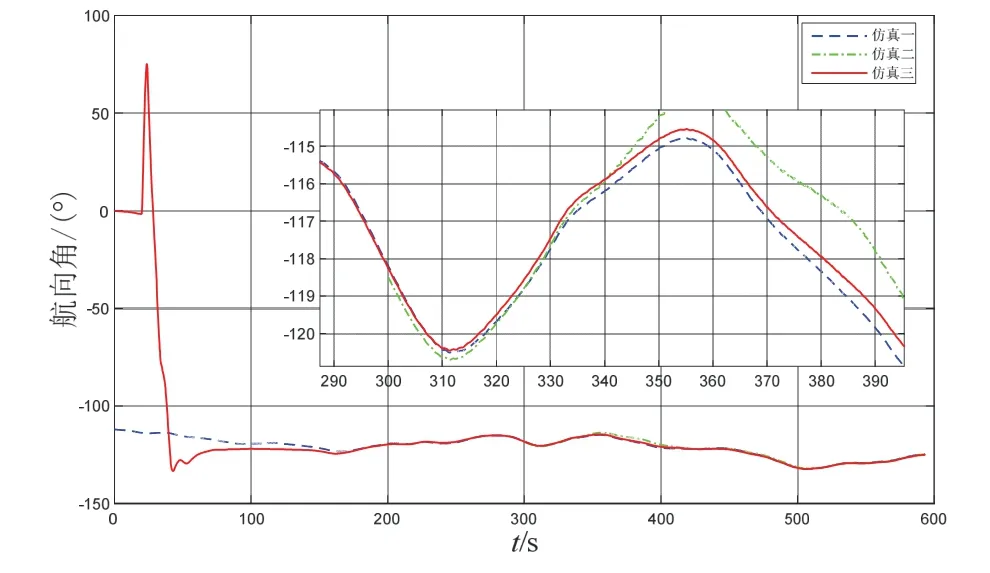
图6 对准过程航向角曲线图及部分放大图Fig.6 The heading angle curve and partial enlarged drawing during alignment
上面的仿真说明,采用双通道时变参数罗经法,能使较大的方位失准角快速收敛;在罗经法进入稳态之后仍存在一定的方位误差,此时切换到卡尔曼滤波精对准状态能进一步提高对准精度。实际上,对于凝固对准,在船舶没有外部参考信息的漂浮状态下,外部环境引入的干扰加速度,都被积分到速度矢量当中,从而导致对准误差的累积,但若缩短凝固对准时间,又会因为不同时刻速度矢量平行度增加,放大对准误差。而对于变参数罗经方位对准,控制回路具有一定的抗干扰性,能抑制误差的放大。
另外要说明的是,本文采用的方法中,将漂浮状态随机的加速度当做等效加速度计的零偏来处理,尽管会降低方案三中的对准精度,但对方案一、二中用于参考的对准方案的影响是一致的。因此表1 中的对比偏差能说明方法的快速性是有效的。
4 结论
本文提出了在粗对准阶段采用时变参数罗经法、精对准阶段采用卡尔曼滤波精对准的方案解决无外部参考信息的情况下船舶SINS 漂浮状态捷联惯导快速自对准问题;在对准初期同时考虑北向通道和东向通道的速度误差且采用时变参数,可使得在任意的大方位失准角条件下都能快速收敛。相比较凝固对准法,在船舶漂浮状态下,本方案能更快地达到相同的对准精度,从而更早地进入卡尔曼滤波精对准,节省对准时间或者在相同时间内提高卡尔曼滤波对准精度。

