面向高维混合不平衡信贷数据的单类分类方法
张东梅,买日旦·吾守尔,古兰拜尔·吐尔洪
新疆大学 信息科学与工程学院,乌鲁木齐830046
在信贷产业迅速发展的今天,建立可信赖的个人信用评分预测模型显得十分重要。个人信用评分指的是对贷款人是否会发生违约行为的一种预测。文献[1]提出了一种更广泛的定义:信用评分是基于客户信用评价水平分析的数值表达,是评估和预防违约风险的有效工具,是信用风险评估的重要方法,是金融风险管理的一个活跃领域。
现实生活中产生的海量数据往往是高维、不平衡的,比如医疗领域、故障检测领域、信贷领域等。如何来存储和提取重要的信息,并对数据进行准确的分类已是一个热门的话题。传统的分类方法虽然能在低维数据中获得较好的分类结果,但在高维数据中处理较为困难。比如在高维的基因表达的数据中,由于许多基因之间可能不相关,并且基因之间存在高度的相关性,文献[2]提出两个阶段的稀疏逻辑回归,通过筛选和采用新的权重作为嵌入方法来获得具有较高分类能力的有效基因子集,达到特征提取的效果。特征选择一般作为减少维度的常用方法[3],但是在样本数量较少且特征数量较大的情况下特征提取就变得很困难,文献[4]提出协同进化的两个阶段来进行特征选择。针对高维有限样本的问题,文献[5]提出采用基于变数自动编码器的降维方法来减少维度。研究者只关注了高维数据问题,很少关注高维混合数据的问题,对于某些基于距离计算的方法,通过采用特征选择的方法减少维度后的数据仍然无法进行相应的数值计算,文献[6]提出Hotelling T2和分类算法结合的多元控制图,用来诊断制造过程中的故障问题,需要用到马氏距离的计算,对于数据中的离散变量需要转化成连续变量再进行PCA(Principal Component Analysis)降维处理,或者仅采用数据中的连续变量进行训练模型,导致原始的数据中某些重要特征失去其原本特性或者直接造成重要特征丢失等问题,这样的数据训练模型相对较差。针对高维混合数据的问题,提出采用PCAmix(Principal Component Analysis of Μixed Data)降维方法,对数据中的离散变量和连续变量同时进行降维处理。在分类问题中除了高维混合的问题,数据不平衡问题在各个研究领域随处可见。对于不平衡数据集,一般处理方法是:(1)对数据进行预处理,使其平衡[7];(2)在分类过程中允许能容忍和稳健的算法来处理不平衡数据[8-9]。
比如在故障检测领域中的故障数据极其少量[10-11]。在电机系统中轴承是重要的工作部件,电机运行中的许多问题与轴承的故障相关,为了解决轴承故障数据较少的问题,文献[12]提出两步聚类算法和过采样方法相结合,并实验验证了提出的方法比直接采取随机森林来诊断故障的方法具有更好的查全率、特异性、AUC和G-Μean评价指标值。
医疗领域的数据大都是不平衡的,比如乳腺癌疾病[13]、帕金森疾病[14]等,通过改进现有的算法来适应不平衡数据,提高模型的预测能力。
在信贷领域,现有的研究方法有线性回归[15]、支持向量机[16]、马尔科夫链[17]和集成方法[18]等。但是信贷数据多数是不平衡的,信誉良好的客户数量远大于信誉不良的客户,文献[19]实现了机器学习和深度学习在不平衡的信贷领域的应用。对于银行来说,把一个“好”客户划分为“坏”客户和把“坏”客户划分为“好”客户的代价是完全不同的。文献[20]研究了类别不平衡和抽样方法对信贷风险分类准确率的影响,不同的分类算法对数据不平衡的敏感程度不同,梯度增强更容易受到样本不平衡的影响。文献[21]提出将特征选择与受限玻尔兹曼机(Restricted Boltzmann Μachines,RBΜ)相结合的信用评分方法,根据RBΜ 的排序标准来选择最佳特征以减少数据的维度,实现了可解释性,在德国数据集上实验得到AUC 值为0.675。文献[22]为了解决原始的BalanceCascade 采样方法不能调节正负样本平衡的问题,加入了可调参数和构建可调数据子集,该方法虽然规避了欠采样的缺点,但引入了大量的参数调整过程,对时间和空间有较高的要求,增加了工作量。
信贷领域的研究很少同时关注到高维混合、不平衡的问题。本文提出采用PCAmix 降维方法来预处理混合数据,然后针对不平衡问题,提出了单类KNN(KNearest Neighbor)计算均值算法。该算法避免了各类采样方法对数据的调整,解决了高维混合、不平衡的数据问题,并且不需要大量的参数设置。
1 算法描述
1.1 PCAmix算法
混合数据主成分分析是由定性变量和定量变量混合描述的一组个体(观察值)而执行的主成分分析。PCAmix 作为一个特殊的案例,包括普通主成分分析和多重对应分析(Μultiple Correspondence Analysis,ΜCA)混合而成。PCAmix 也是一种降维方法,旨在减少数据维数,并识别变量之间的相似度,同时也识别观测变量之间的相似度。对于大多数的高维数据集不仅包含定性变量也包含定量变量,采用PCA或者ΜCA降维并不能得到很好的效果,因此提出采用PCAmix方法对混合数据进行降维处理,它结合了PCA和ΜCA各自的优势。
PCAmix方法使用的符号采用文献[23]的介绍:
n 为观测单元的个数,p1为定量变量的个数,p2为定性变量的个数,p=p1+p2,p 为总的变量的个数。
如果第j 个变量是定量的,设Zj为列向量,其中包含变量j 上n 个对象的标准化得分。
如果第j 个变量是定性的,设Gj为变量j 的指标矩阵,Dj为该变量类别频率的对角矩阵。
m 表示定性变量p2的类别数。
PCAmix 算法的实现过程:假设k 为PCAmix 中所要求的目标维度数目,计算标准化得分的n×k 的矩阵X ,各分量的得分方差和p×k 矩阵C 的平方荷载,平方荷载就是定量变量的平方和定性变量的相关比。
PCAmix关于定性变量和定量变量的降维计算步骤如下:
步骤1 计算大小为n×n 的量化矩阵Sj:

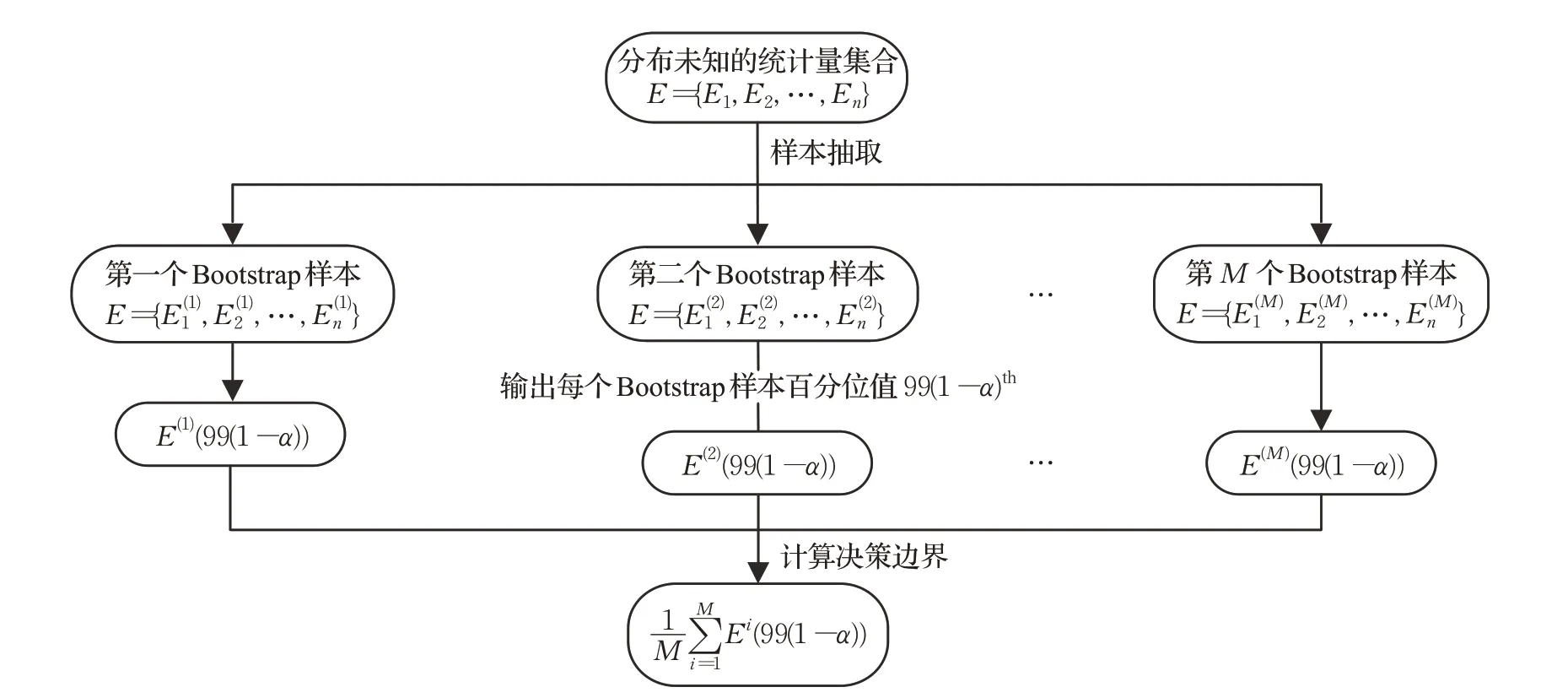
图1 Bootstrap方法图解介绍
步骤2 计算n×n 矩阵S:

步骤3 对S 进行特征值分解,标准化分量得分的矩阵X ,是由标准化为n 个S 中的前k 个特征向量给出(Ik是单位向量):

步骤4 计算第l 个分量的方差,l=1,2,…,k,Xl代表X 的第l 列,计算公式如下:

步骤5 计算P 个变量的前K 个分量的平方荷载矩阵C ,Cjl表示变量j 与分量l 之间的平方相关(j 取的是特征变量,l 为某一特征的所有取值),Cjl计算如下:

PCAmix降维方法与PCA和ΜCA方法的区别在于对定性变量和定量变量的计算处理上。上述的计算过程中,所有的变量是定量变量时,相当于PCA 降维方法,所有的变量取值是定性变量时,则相当于ΜCA方法。
1.2 单类KNN 计算均值算法
(1)假设正例样本为X={x1,x2,…,xn},负例样本为Z=(z1,z2,…,zm),输出值Y={0,1},Y=1 表示正例样本,Y=0 表示负例样本。
(2)假设训练样本T=(T1,T2,…,Ti)⊆X(i <n),每个样本点Ti距离周围最近的k 个正例样本的每个样本取值为P={P1,P2,…,Pk},k 表示每个样本距离周围最近的正例样本的邻居数。
(3)训练阶段,采用欧式距离计算训练样本间的距离:

(4)测试阶段,将剩余正例样本C={C|c ∈X,且c ∉T}和负例样本Z 组合成测试样本(未知标签的测试数据),采用式(6),计算出每个测试样本E 与距离最近的k 个训练样本T 的距离的平均值。
(5)假设每个测试样本计算出的距离均值为D(不同的样本所计算得到的D 基本不同)。
(6)采用Bootstrap方法来自定义决策边界,Bootstrap的图解介绍如图1所示。
(7)将(4)中计算得到的每一个测试样本值D 与(5)得到的99 组决策边界Ql{l=1,2,…,99}进行比较,对于该样本的预测输出结果如下:

1.3 单类支持向量机
单类支持向量机(One-Class Support Vector Μachine,OC-SVΜ)参考文献[24]的介绍。OC-SVΜ 算法是在特征空间中求解出一个最优的超平面实现目标数据距离坐标原点的最大的分隔,模型介绍如下:假设存在数据样本X={X1,X2,…,Xi},核函数Φ 的作用是将低维的线性不可分映射到高维的线性可分。OC-SVΜ 模型介绍如图2所示。

图2 OC-SVΜ模型示意图
OC-SVΜ 算法中坐标原点被当作一个唯一存在的异常点,最优超平面和坐标原点的最大距离为ρ/‖ ω ‖,允许少数样本在坐标原点和超平面之间,这些样本到超平面的距离计算是ξi/‖ ω ‖,ω 代表支持向量的权重,阈值为ρ,决策函数为式(8):

其中,变量ρ 和ω 通过式(9)求解获得:

变量v ∈(0,1),是用来决定支持向量在训练模型过程中样本的权重占比。把核函数的概念引入后,相应的问题就转化成了对偶问题,描述如式(10)所示:

1.4 K 近邻算法
K 近邻(K-Nearest Neighbor,KNN) 算法的原理是:在一个样本空间中找到与其最近的k 个样本,其中这k 个样本是已知标签类别的样本,统计输入的样本在整个已知标签的样本空间中的k 个样本的类别,其中所占的类别数目较多的,就作为该预测样本的类别。在KNN 算法中,要对未知样本进行类别划分,所选择的k个邻居一定是已知类别样本。
2 实验内容与结果分析
为验证本文提出的基于PCAmix 降维预处理的单类KNN 计算均值算法的有效性,本文选用经典的OCSVΜ算法和KNN 算法,分别基于PCA和PCAmix方法降维处理,并与文献[25-26]在该数据集上进行比较,分类效果从可视化的ROC(Receiver Operating Characteristic,ROC)曲线图、AUC(Area Under the Curve)值和F1值等多个角度进行评价。用于实验的数据是UCI上公开的German credit 和Default of credit card clients(Default credit)信贷数据集。
在参数选择方面,本文提出的单类KNN 计算均值算法的最佳决策边界通过Bootstrap 方法选取,其1-α取值为{0.01,0.02,0.03,…,1.00},共100 组取值,选择其中使得F1 值最大的1-α 值,作为计算训练模型的决策边界。
2.1 数据预处理
由于PCA 降维方法是通过计算协方差矩阵获得,对于数据中的离散变量需要转换成连续型的数值变量,再进行PCA降维处理。
2.2 评价指标
对于一类分类问题,AUC值是最常用的评价指标,计算公式为:

AUC通常用于评价一类分类器和新颖性检测,AUC值是ROC 曲线下的面积,其中真正例(True Positive,TP)、假正例(False Positive,FP)、真反例(True Negative,TN)和假反例(False Negative,FN)分别是真实类别与学习器预测类别的组合划分,又叫作混淆矩阵,解释如表1所示。
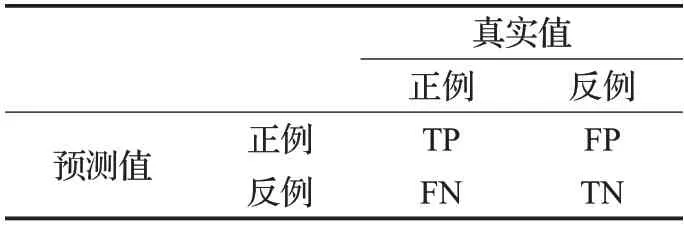
表1 混淆矩阵
F1 值(F1 score)用于衡量二分类模型的精确度,可以看作模型精确率(Precision,P)和召回率(Recall,R)的一种调和平均,取值范围为0~1,计算公式为:

其中P、R 的计算公式为:

ROC 曲线是实验准确性的综合性代表,其横坐标代表假正例率(False Positive Rate,FPR),表示所有负例中,错误识别为正例的负例比例;纵坐标代表真正例率(True Positive Rate,TPR),表示所有正例中,正确识别的正例比例。计算公式如下:

PR 曲线的横坐标为召回率R ,纵坐标为精确率P,作为同一算法中不同条件下的分类效果的可视化度量,如果一种情况下的PR 曲线能完全包住其他情况下的PR曲线,则证明该情况下的算法是更有效的。
2.3 数据描述
本文采用来自UCI 中的German credit 和Default credit 信贷数据集,这两个公开的信贷数据集均具有高维混合、不平衡的数据特点。
数据集的详细介绍如表2所示。

表2 数据集介绍
2.4 实验过程
由于Default credit信贷数据集的数据量较大,为了图形的可视化效果,按照Default credit的数据不平衡比率对其进行随机抽样,抽取3 000条数据进行实验。
实验数据划分如表3所示。

表3 实验数据划分
2.4.1 单类KNN 计算均值算法
(1)模型训练阶段
在训练模型之前,分别采用PCA和PCAmix方法进行降维预处理,在训练模型时仅采用多数类(正例样本)进行训练,计算训练数据的邻近的k 个样本的距离均值。
(2)决策边界选取
采用Bootstrap方法来定义决策边界,通过统计训练数据的1-α 的各个指标均值统计量,选择其中使得F1值最大的1-α 统计量作为决策边界。
German credit 数据经过PCAmix 和PCA 降维处理的最佳决策边界周围的5组统计量如表4和表5所示。

表4 German credit经过PCAmix降维的5组决策边界统计

表5 German credit经过PCA降维的5组决策边界统计
Default credit 数据经过PCAmix 和PCA 降维处理的最佳决策边界周围的5组统计量如表6和表7所示。
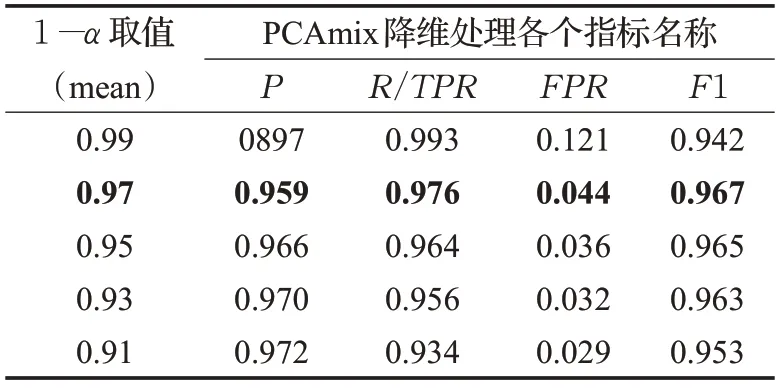
表6 Default credit经过PCAmix降维的5组决策边界统计

表7 Default credit经过PCA降维的5组决策边界统计
表3、表4、表5和表6的结果显示,关于German credit数据和Default credit 数据的PCAmix 降维处理的最佳决策边界的1-α 取值分别是0.95 和0.97,PCA 降维处理的最佳决策边界1-α 取值分别为0.89和0.93。
(3)模型测试阶段
通过训练数据选择出了最佳的决策边界以后,对测试数据进行预测。从图像的可视化效果来看,正负样本可以找到最佳的决策边界,来最大限度地对测试数据进行分离,为了体现算法的预测效果,将训练数据通过散点图来体现。
German credit 数据和Default credit 数据经过两种降维方法预处理的测试数据散点图如图3和图4所示。
(4)实验结果
在PCA 和PCAmix 降维预处理的单类KNN 计算均值算法中,为了体现PCAmix降维条件下的单类KNN计算均值算法更加有效,通过PR曲线图来可视化体现。两种数据在PCA和PCAmix降维预处理条件下的PR曲线如图5所示。

图3 German credit数据两种降维方法的测试数据散点图

图4 Default credit数据两种降维方法的测试数据散点图

图5 单类KNN 计算均值算法的PR曲线图
从图5 中观察到PCAmix 降维处理下PR 曲线完全包住PCA降维条件下的PR曲线,体现出在本文提出的单类KNN 计算均值算法中,PCAmix 对混合数据的降维处理优于PCA。
2.4.2 OC-SVM算法
为了验证OC-SVΜ 在PCAmix 降维预处理实验中的效果优于PCA 降维预处理,通过ROC 曲线图来体现实验结果。
两种数据在PCA 和PCAmix 降维预处理条件下的ROC曲线如图6所示。
从图6 的ROC 曲线图观察到,OC-SVΜ 算法在PCAmix和PCA降维预处理下的实验效果均不理想,但此信贷数据集上的OC-SVΜ 算法模型在PCAmix 降维预处理条件下的效果略优于PCA降维方法。
2.4.3 K 近邻算法
为了验证K 近邻算法在PCAmix 降维预处理的实验效果优于PCA 降维预处理,实验的K 值选择与单类KNN 计算均值的取值相同。实验结果也采用ROC 曲线来体现。
两种数据在PCA 和PCAmix 降维预处理条件下的ROC曲线如图7所示。
从图7的ROC曲线看出,PCAmix降维处理的K 近邻算法模型优于PCA降维处理。
2.5 实验结果与对比
为了突出本文提出的单类KNN 计算均值算法的优越性,实验结果不仅统计两种数据在不同降维处理条件下的各类算法的AUC 值,还与前人在此数据集上的二分类算法进行AUC值对比。
German credit数据的AUC值对比如图8和表8所示。
Default credit数据的AUC值对比如图9和表9所示。
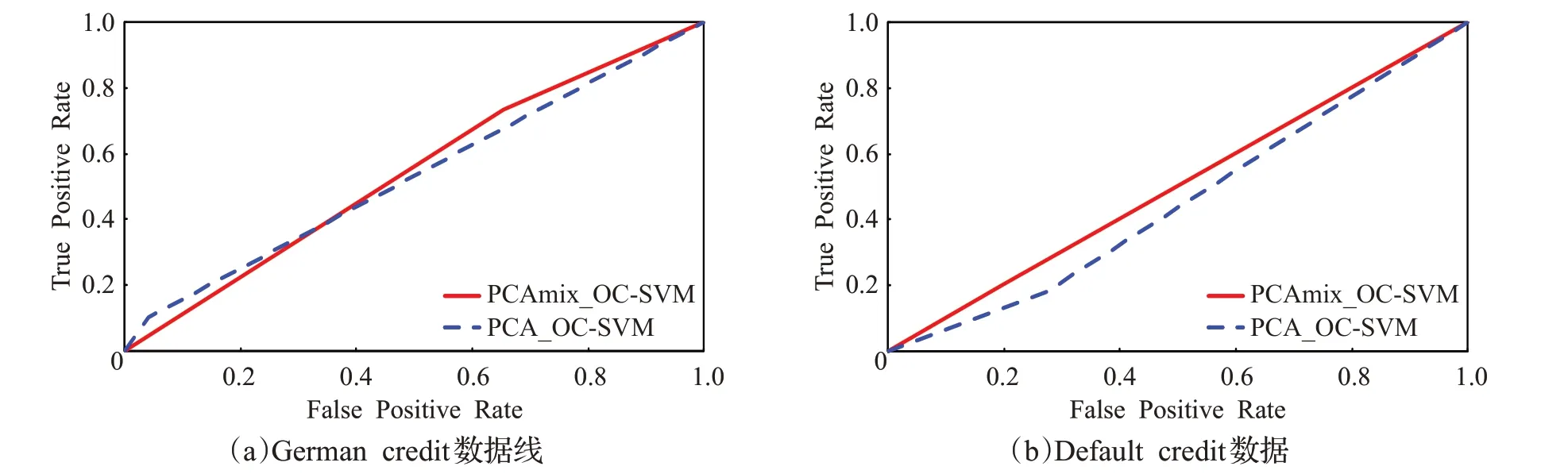
图6 OC-SVΜ算法模型的ROC曲线

图7 KNN 算法模型的ROC曲线图

图8 German credit数据的各类算法性能对比

表8 German credit数据上各类算法的AUC值对比

图9 Default credit数据的各类算法性能对比

表9 Default credit数据上各类算法AUC值对比
从实验结果看出,本文提出的PCAmix降维处理的单类KNN 计算均值算法在处理面向高维混合且不平衡的信贷数据上效果更佳。
3 结束语
本文采用PCAmix降维方法预处理高维混合数据,提出单类KNN 计算均值算法,并在不平衡的German credit 和Default credit 数据集上进行实验,实验结果表明采用PCAmix 降维处理高维混合数据要优于PCA 降维方法,而且提出的单类KNN 计算均值算法在处理不平衡的信贷数据上有较好的性能。但是单类KNN 计算均值算法能否适合各类不平衡领域的研究还是未知的。因此,接下来计划在医疗领域和工业质量检测领域等来研究该算法的泛化性能。

