基于功率谱密度与卷积神经网络的心音分类
许春冬,辛鹏丽,周 静,应冬文,2
1.江西理工大学 信息工程学院,江西 赣州341000
2.中国科学院大学 电子电气与通信工程学院,北京100049
心血管疾病是全球患病率及疾病致死率的主要因素之一,在影响人类社会活动的同时,更严重危害着生命健康[1]。针对心血管疾病诊断的难题,出现了一系列辅助诊断方法,如心电分析、心音分析、CT检测等[2]。其中,心音信号是由心脏进行周期性泵血运动产生的振动,经人体组织传导于体表形成的一类声学信号,能够反映心房、心室、瓣膜、动脉血管壁等结构的工作状况,这也就使得通过心音来分析心血管疾病是可行的[3]。心音听诊是心音信号分析中常用的方法,被广泛应用于临床诊断中。然而,精确的听诊往往依赖于医师的长期训练经验,而这一过程又耗时耗力,因此需要一个用于心音分析的计算机辅助工具来协助诊断心血管疾病[3-4]。相比于其他辅助诊断方法,心音信号分析具备操作简便、完全无损、成本低廉、便于远程诊断、效率高等特点,且可检测出初期的心血管疾病,能够起到早检测早治疗的关键性作用[5]。
心音分析系统中,对正常与异常心音信号的分类方法研究最多,主要用于辅助医师完成初步诊断,实现精确检测,以节省医疗资源和成本[5-6]。在心音信号正常与否的判定问题中,研究者们提出了一系列方法。Gupta等人[7]提出了结合同态滤波和K 均值聚类的心音信号的小波分析分割方法,将分割结果形成特征向量,在两类异常和一类正常心音分类中准确率达到97%,但当异常心音种类增多时分类精度明显下降;Dokur 等人[3]提出通过离散小波变换加窗的方法完成心音的分割与特征提取,采用增量自组织映射网络进行分类,但在处理噪声环境复杂的心音时其分割及特征识别结果并不理想;Wang 等人[8]提出采用25~400 Hz 的巴特沃斯滤波器结合基于逻辑回归的隐半马尔科夫模型提高分割精度,最终获得74.9%的分类结果;Zhang等人[9]提出了一种基于缩放图谱和张量分解的特征提取方法,并通过支持向量机完成分类,在数据集C上取得了90%的分类结果。上述研究存在一个共同的问题,即在提取特征前要先有效地完成分割。然而,分割问题一直是心音信号分析中极具挑战性的难题,到目前为止还没有一种完美的分割方案。因此一些学者提出了直接提取整个心音段或心动周期的特征进行识别,从而规避因分割问题给系统带来的误差[10]。郭兴明等人[11]提出了基于经验模式分解和关联维数的心音特征分类方法,但心音信号具备多样性,仅仅依靠关联系数无法把握心音信号的本质特征;汪晶[10]提出了多阈值融合心音递归图和局部线性嵌入算法降维小波系数自相关特征的特征提取算法,但其时耗性高,且处理复杂病理心音效果不理想;Deng等人[12]提出将子带包络与自相关特征融合获取扩散图统一特征的分类方法,但在噪声干扰较强时容易提取到噪声信号;Singh-Μiller 等人[13]提出通过特征谱图的均值、方差等特征来完成分类任务,同样容易受噪声干扰。
基于上述分类问题中遇到的难题,本文提出了一种基于功率谱密度(Power Spectral Density,PSD)时频特征的正常与异常心音分类方法,通过有效的预处理和特征提取过程,采用卷积神经网络(Convolutional Neural Network,CNN)分类器,在Challenge 2016 数据集中获得了良好的评价指标。
1 算法框架
本文提出了一种基于功率谱密度时频特征的正常与异常心音分类方法,主要包括预处理、检测心动周期并分段、提取PSD时频特征矩阵、特征矩阵填补、构建分类器、分类器训练与测试等,如图1所示。首先,采用小波降噪的方法抑制心音中噪声的干扰;然后,采用自相关法检测心动周期,并按相关包络分段出第一个心动周期,并对剩余部分循环提取,避免长时采集心音的自相关包络带来的心动周期误差;获取心动周期集后,即可提取心动周期的PSD时频特征,并通过双线性插值法将周期略短的心动周期PSD 特征进行补齐处理。根据Challenge 2016 的训练集与测试集数据,获取训练特征集和测试特征集,送入构建的CNN 分类器进行迭代训练,并通过测试进行泛化能力检验,从而获得有效的正常与异常心音分类模型。

图1 算法原理图
2 PSD时频特征的提取
针对心音分类,学者们提出了大量基于时域特征的分析方法[4]。然而,与时域分析相比,频域分析往往更具优势,因为特定信号具有较为稳定的频带,而时域却呈现较强的非平稳性[3-4]。频域分析是一种较好的标准化分析工具,在许多临床和生理现象中都得到了应用[4,9]。正常心音与异常心音在频谱的分布上存在一定的差异,主要源于三尖瓣、二尖瓣、主动脉、心肌等结构工作状况不同。在正常心音中能够听到清晰的第一心音(s1,10~140 Hz)和第二心音(s2,10~200 Hz),在部分儿童心音或异常心音中可听到第三心音(s3,10~70 Hz),第四心音(s4,10~70 Hz)主要出现在异常心音中[14]。文献[15]指出,异常心音在收缩期、舒张期会产生大量心杂音,且频带范围较正常心音更高,部分异常心音频率可达600 Hz左右。功率谱密度能够联合时频域特征,较好地描述心音信号的时频分布特征,故本文将通过功率谱密度分析对心音特征进行量化。
2.1 心音信号的预处理
心音信号来源于心脏泵血的机械振动,极易受到各类噪声的干扰。因此,在对心音信号进行分析前,需进行降噪处理。小波降噪是心音分析中应用最广的降噪方法,本文采用了小波降噪的方法,对心音信号进行了降噪处理。小波降噪的原理是通过小波系数来区分各尺度内的噪声与信号,其关键在于阈值函数的构建,本课题组对小波降噪进行了深入的研究,具体算法请参考文献[16]。图2 给出了随机选取的四条心音记录(均来自Challenge 2016 数据库[14])采用小波降噪方法降噪后的结果,可以看出该方法有效地抑制了噪声,提升了心音信号的可分析性。
2.2 心动周期的检测

图2 降噪结果
心音信号具有显著的周期性特征,其正常与否的特点通常在心动周期中能够得到完整的体现。在功率谱特征的提取中,以心动周期为分析对象,获取心脏每个循环供血过程中的细节特征,来判断心脏工作的正常与异常。准确检测心动周期的长度是检测心音心动周期的前提。文献[5]指出,通过自相关的方法能够较为准确地获取到心动周期的长度。然而,在长时采集心音段的自相关包络中,由于后期的平滑处理,随着时间的延长,无法保留心动周期的变异性特征,甚至使得用于区分心动周期的包络特征变得模糊,如相关包络变得矮小不利于波峰提取,如图3所示。通过将心音信号划分为一定长度的分析窗可以避免此类问题。本文采用自相关法检测心动周期T[4-5],并根据T 将心音信号分段为心动周期,其流程如下:
(1)心动周期长度一般在0.6~1.2 s 之间,将待处理的心音以4 s为时长取出心音的第一个时窗。
(2)按照式(1)计算时窗内心音的自相关:

其中,mT为时窗内第mT帧,mT=0,1,…,N,N 为时窗内总的帧数,Fr(lenT) 为短时平均能量,Frame 为帧长。在获取心动周期时取自相关大于等于0部分即可,并做中值滤波处理,平滑包络曲线。图3展示了一条预处理后的心音段自相关包络的提取结果。
(3)提取自相关包络的波峰,记0 处的第一个波峰为P1,以0.5~1.5 s 采样点为区间搜索下一个最高波峰P2,则P1~P2的时段即为第一个心动周期T1。
(4)跳过P2前的时段,以P2为新的波峰起点,重复步骤(3),搜索下一个波峰P3,获取下一个新的周期T2。
(5)从心音中去除已检测的前两个心动周期部分,获取新的时窗,并重复步骤(2)、(3)、(4),直到需要被检测的剩余心音不足一个时窗的长度。
2.3 功率谱密度时频分布矩阵的提取
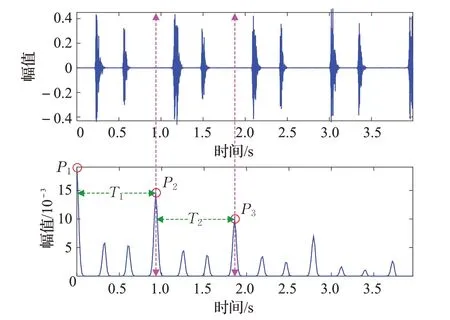
图3 心动周期的检测
常用的功率谱估计方法主要有周期图法、间接估计法、Bartlett估计法、Welch估计法四类[17]。周期图法又被称作直接估计法,其过程为先将待估计的信号x(n)进行快速傅里叶变换(Fast Fourier Transformation,FFT),然后取幅值平方并做平均得到估计值;Bartlett估计法是在周期图法的基础上按照分段求周期图再取平均的方式进行优化改进,改善了谱曲线的不稳定和分辨率问题;Welch 估计法则是在Bartlett 估计法的基础上增加了加窗分帧和帧移,避免谱估计为负并减小方差[18]。本文采用Welch估计法来估计心音信号的PSD,其步骤如下:
(1)根据fs=2 000 Hz 的采样率,取窗长为win=30 ms,一是根据短时平稳性使每一窗心音的PSD 具备平稳性,二是使得心音PSD在时间域上具备较高的分辨率。帧移取inc=15 ms,使得PSD在时间域上具备较好的平滑性,按照窗长对信号进行分帧:
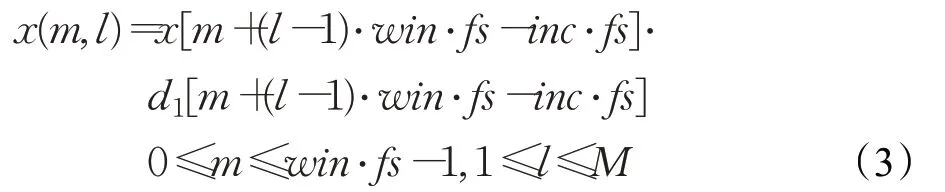
其中,m 为帧内时域样点,l 表示第l 帧,M 为总帧数,d1为窗函数。
(2)通过Welch 算法估计心音帧的功率谱密度PSD(w):

其中,d2表示数据窗口,U 为归一化因子。
(3)取对数获得功率谱密度- -- ---PSD(w):

(4)对功率谱密度进行正向归一化处理:


上述过程中,窗函数的选择对功率谱存在一定的影响,故测量了矩形窗(Boxcar)、海明窗(Hamming)、布莱克曼窗(Blackman)三类窗函数下功率谱密度的结果。图4 给出了三类窗函数下一组心音信号PSD 均值的估计结果。可以看出,相比Boxcar 窗和Blackman 窗,Hamming 窗能够有效抑制低频成分,突出基础心音频带,更为适用于心音信号的PSD估计。采用Hamming窗提取的正向归一化PSD 特征如图5 所示。因此,d1和d2为Hamming窗。

图4 不同窗函数下正向归一化PSD均值的估计
2.4 双线性插值法填补功率谱密度特征矩阵
第2.2节采用自相关法检测心动周期并将心音信号分段为心动周期集,但心音具备多样性,且心动周期间也具备心率变异性,这就使得分段出的心动周期长度并不一致,即每个心动周期帧数不一致。因此,心动周期集所求取出的功率谱密度特征矩阵大小也是不同的,而分类器输入端的大小一般是固定的,故要求功率谱密度矩阵的大小一致。文献[9]指出,可通过双线性插值法来填补心动周期频谱图,本文采用此方法填补心动周期功率谱密度矩阵,使得各心动周期功率谱密度矩阵大小一致。

图5 正向归一化PSD特征
双线性插值法心动周期功率谱填补的目的不是要在时间刻度上延长获取更多的矩阵元素,而是在原始时间刻度内增加功率谱密度帧数,从而提升时间维度的分辨率,这样可以保持心动周期内的频谱分布基本保持不变。心音功率谱密度矩阵的双线性插值法填补流程主要由以下四个步骤组成[9]:
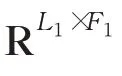

(2)第i 个时间尺度点和第j 个频率尺度点的插值因子为:

其中,round 表示四舍五入取整运算。
第i 个时间尺度点和第j 个频率尺度点插值因子的绝对值偏差为:

(4)重复步骤(2)、(3),直至完成所有插值点的计算。
在心音信号的功率谱密度时频矩阵填补中,只需填补时间尺度点,无需填充频率尺度点。这是因为频率尺度只与短时傅里叶变换的窗长有关,固定窗长其频率尺度则一致;而时间尺度与心动周期长度相关,这恰是需要填补的。图6给出了a0001中某一心动周期的填补结果,可看出时间轴长度不变,但增加了帧数。

图6 双线性法填充特征矩阵
3 构建CNN分类器与数据集
用于心音的分类器主要包括支持向量机(Support Vector Μachine,SVΜ)分类器、反向传播神经(Back Propagation,BP)网络分类器、自组织映射(Self-Organizing Μapping,SOΜ)网络分类器、隐马尔科夫模型(Hidden Μarkov Μodel,HΜΜ)分类器、循环神经网络(Recurrent Neural Network,RNN)分类器、长短时记忆网络(Long Short-Term Μemory Network,LSTΜ)分类器和卷积神经网络(CNN)分类器。其中,SVΜ 分类器、BP神经网络分类器不具备自主优化特征的性能[9];HΜΜ分类器多借助于高斯混合模型进行分类,当正常与异常心音时域分布类似时容易出现分类误判[5,8];RNN 分类器处理时间序列效果较好,但存在梯度消失和爆炸的问题;LSTΜ网络在RNN基础上,增加了门单元,解决了梯度消失和爆炸的问题;CNN 分类器相比前几类分类器模型,能够较好地处理多维数据,挖掘局部结构特点[19-20]。CNN 已经在图像处理领域取得了显著成绩,而心音PSD 时频矩阵与图像相同为二维矩阵,因此CNN 分类器更为适用。
CNN 是一种融入卷积结构的深度前馈神经网络,主要由输入层、卷积层、激励层、池化层、全连接层、输出层组成[19,21]。其中卷积层、激励层与池化层可进行交替连接,能够有效地降低数据维度,提高模型的容错能力。在CNN 分类器构建过程中,通过在有限范围内进行随机搜索,能够确定较为合适的卷积层数和卷积核大小。构建的CNN分类器的结构如图7所示。
实验中将99×41 的特征矩阵去除频率尺度点为0、时间尺度点为0 所对应的行与列,构成98×40 的输入矩阵,通过分类器并进行二分类。构建的CNN 分类器共计两次卷积运算,第一卷积层的卷积核大小为5×5,数量为32,卷积水平步长为1,最大池化层为2×2,选择ReLU函数为激励函数,则第一次卷积运算后每个卷积核中的数据被压缩为94×36 的特征图,池化后特征图大小为47×18;第二卷积层卷积核大小为2×3,数量为64,卷积水平步长为1,最大池化层为1×4,激活函数仍选择ReLU,则第二次卷积运算后每个卷积核中的数据被压缩为46×16 的特征图,池化后特征图大小为23×8;共三层全连接层,第一全连接层为1×1 024,第二全连接层为1×512,第三全连接层为1×256;输出层为1×2,输出结果为01 表示正常,输出结果为10 表示异常。部分训练参数设置如表1 所示,其中B 为下采样层的map 的权值,Dropout为防止过拟合的trick。

表1 网络参数设置

图7 CNN分类器网络结构
通过训练数据集对CNN 分类器进行迭代训练,并通过分类正确率和损失函数两类指标对分类器进行评价。分类器为二分类器,损失函数采用常规的交叉熵损失函数即可。正确率ACC 和损失函数LOSS 评价指标的定义如式(19)、(20)所示:

其中,TP 为正常心音分类正确数,TN 为异常样本分类正确数,FN 为正常心音分类错误数,FP 为异常样本分类错误数。 N 为样本总数,Osamp为第samp 个样本真实标记值,Ȏsamp为第samp 个样本预测值。
需要进一步说明的是,TP、TN、FP、FN 是通过心音记录心动周期的分类,完成心音记录的判别获得的。其中设置了容错机制,即心音记录中,异常心动周期数与心动周期总数比例小于10%时,判定心音记录为正常,否则判定为异常。
选用Challenge 2016 数据集[14]构建训练集与测试集。整个数据集由a、b、c、d、e 这5 个子数据库构成,分别采集于1 000多位不同年龄、不同性别、不同身体状况的受试者,共计3 126 条心音记录。按照官方给出的数据构建测试集,从5个子数据库中选用301条心音,除去测试集,训练集共计2 825条心音。
4 实验结果与分析
按照预处理、周期检测、PSD 时频特征提取的流程获取PSD时频特征数据集。其中训练集2 825条心音中检测出84 762个心动周期,测试集301条心音中检测出7 326个心动周期,最终构成98×40×84 762的训练集,98×40×7 326的测试集,均按列存储,生成.mat的数据文件。

图8 训练结果
分类器在训练集作用下经过100次迭代训练,其结果如图8所示,训练集与测试集在分类器中获得的结果如表2 所示。图8 训练结果显示,迭代训练60 次左右ACC 和LOSS 值均基本收敛,收敛后ACC 值为88.70%左右,LOSS 值为1.084 4左右。训练完成后,测试集在网络中的ACC 为84.72%,LOSS 值为1.185 7。

表2 训练集与测试集结果
此外,灵敏度(Sensitivity,Se)和特异性(Specificity,Sp)[20,23]被广泛用于评价分类系统的性能。灵敏度和特异性计算方法如式(21)和式(22)所示:

其中,WA1、WA2、WN1、WN2为权系数,分别为官方标记的正常情况下可分析性好坏的心动周期数量比例以及异常情况下可分析性好坏的心动周期数量比例;N表示标记为正常的心音,A 表示标记为异常的心音,n表示分类输出为正常的心音,q 表示分类输出不确定的心音,a 表示分类输出为异常的心音,下标1 表示心音可分析性良好,2表示心音可分析性较差。权系数取值如表3所示。

表3 心动周期比例权系数
本文算法在训练集和测试集中获得的灵敏度与特异性结果如表4所示。其中训练集灵敏度为0.834 8,特异性为0.959 8,整体得分为0.897 2;测试集灵敏度为0.776 3,特异性达到0.946 3,整体得分为0.861 3。

表4 灵敏度与特异性
本文算法同自相关&扩散图特征&SVΜ[12]、分割后多维特征&非线性径向基SVΜ[8]、光谱图&SVΜ[9]、分割提取324 维特征&BPANN[22]、热谱图&CNN[19]、AdaBoost&CNN[23](官方网站公布数据)算法进行了对比。文献[12]采用小波分解提取四层分解中第四细节系数层和第二细节系数层的系数,通过香农包络自相关特征,并通过扩散图映射到对应空间,通过几何空间中特征的欧氏距离采用SVΜ 进行分类,但小波分解层次选择中存在有用信息丢失的风险;文献[8]与文献[22]方法相似,均是通过被动提取多维特征后采用分类器进行分类,这往往又与特征的好坏有关;文献[9]将傅里叶变换后的频谱特征通过偏最小二乘法进行降维,然后通过非线性SVΜ进行分类,但非线性SVΜ并不适用于偏最小二乘降维后的数据分类[24];文献[19]将Μel 频率倒谱系数(Μel Frequency Cepstral Coefficient,ΜFCC)特征转换为热谱图,采用SVΜ对其进行分类,然而ΜFCC是基于人耳的听觉特性,用于心音信号特征的表征能力往往有限[25];文献[23]提取了心动周期4个成分25~400 Hz中的9个频带和13维的ΜFCC特征,按照25~45 Hz、45~80 Hz、80~200 Hz、200~400 Hz集合特征训练CNN分类器,并采用AdaBoost 算法将4 个CNN 组合构成强分类器,但分类的结果仍取决于提取的特征,且没有计算4个频带间的过渡信息;本文算法提取心动周期的功率谱密度特征,构成二维时频特征矩阵,采用CNN分类器主动提取特征,降低了被动提取特征的风险,使得特征更适应分类器,获得更强的分类性能,事实上这在许多图像分类领域中已经得到了体现。
上述实验的SVΜ 模型中,除了文献[8]选用了非线性径向基核函数外,其余均选择Sigmoid核函数,参数σ和惩罚因子c 的取值为(2,2),详细的模型描述请参考具体文献。
对比实验结果如表5所示。实验结果表明,在SVΜ分类器下,PSD时频特征最终获得了0.830 0的得分,较自相关与扩散图特征(0.754 9)、光谱图降维特征(0.784 1)、分割提取特征(0.782 6[8]、0.828 6[22])的方法得分更高,这也进一步说明PSD 时频特征矩阵能够用于心音分类。此外,与分割提取324 维特征&BPANN、热谱图&CNN、AdaBoost&CNN 等算法相比,本文算法获得了较好的Sp 得分(0.946 3),Se 得分(0.776 3)相对较低,但与热谱图&CNN算法相比提升了0.048 5,且获得了较好的总体评分0.861 3。从表5 中的对比结果可以看出,相比SVΜ 分类器而言,PSD 时频特征在CNN 分类器下具备更好的分类效果。从算法整体评价结果来看,在测试集中取得了不错的效果,这也进一步说明本文提出的分类算法具备可行性与有效性,即所构建的CNN 网络能够有效区分正常心音与异常心音的PSD特征矩阵。
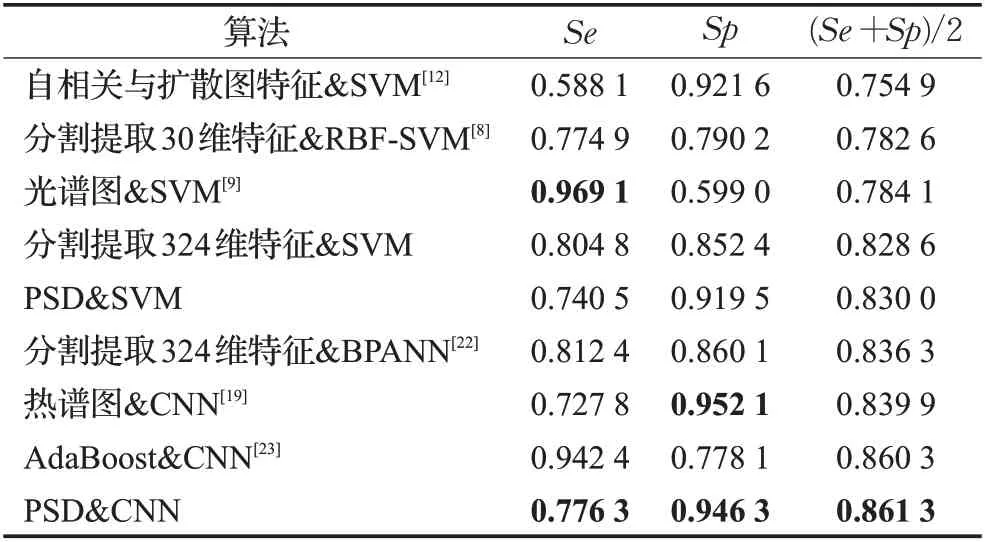
表5 不同算法下测试集评价指标的对比
5 总结与讨论
本文提出了一种基于功率谱时频特征和CNN的正常与异常心音分类算法,无需进行心音分割,且具备较好的分类效果。处理中,首先进行小波降噪预处理,提高数据集的可分析性;然后,通过自相关法检测出有效的心动周期,并采用Welch法提取功率谱特征;接着,采用双线性插值法填补各心动周期,保持帧数一致。针对于特征矩阵数据集,构建了CNN分类器,并采用Challenge 2016数据集获取训练集和测试集,并进行训练和测试。实验结果表明,本文算法在评价体系中分类正确率和特异性等指标较好,但在灵敏度上需进一步提升。同时,本文算法无需进行心音分割,避免了分割带来的误差和增加算法复杂度,且本文算法可为现代心音信号分析与处理提供技术性参考。此外,建立在准确心血管疾病心音记录数据集的基础上,本文算法可进行推广,应用于具体异常类型的心血管疾病筛选与检测。

