基于Super-twisting算法的永磁同步电机自适应滑模速度控制

汤 成，胡继胜

（大连交通大学 机车车辆工程学院，大连116028）

永磁同步电机（PMSM）因其具有高效率、低能耗、功率密度高、转矩大、噪声小及可靠性高等多重优势[1]被广泛应用于风力发电、电动汽车、轨道交通各个领域中[2-4]，由此对PMSM 系统的控制精度、控制稳定性也提出了更高的要求。传统的PI 控制作为一种经典控制策略因其算法理论较为简单、稳定可靠在工业控制领域受到广泛应用，但因PMSM 是一个非线性、强耦合、参数可能随时间变化的复杂系统，PI 抗干扰能力又较差，难以满足对PMSM 高精度控制的要求。因此，诸如滑模变结构控制（SMC）[5]、自适应控制[6]、遗传算法控制[7]等新型控制开始被提出。其中，滑模变结构控制因其响应速度快、抗扰动能力强等优点，被众多专家学者加以深入研究以应用到PMSM 系统中。文献[8]基于传统指数趋近律，引入了变指数函数和双曲正切函数，提高了系统趋近速度和抖动抑制能力。文献[9]提出了一种基于改进的幂次指数趋近律的模糊自适应滑模控制器设计方法，引入了积分滑模面和模糊自适应方法优化趋近律未知参数。文献[10]在幂次趋近律的基础上加入指数项，并且在幂次指数项指数中引入系统状态变量使幂次指数与系统状态关联，解决幂次趋近律在原理滑模面时趋近速度慢的问题，同时使系统平滑进入滑模面。

综上所述，本文在自适应滑模速度控制器[11]的基础上，引入了Super-twisting 滑模控制。Supertwisting 滑模控制属于二阶滑模控制方法，相较于传统的滑模控制，由于可以产生连续的无抖振控制信号，还可以实现滑模变量及其导数在有限时间内渐进稳定，所以其控制性能更加优越。

1 PMSM 数学模型

同步旋转d-q 坐标系下PMSM 定子电压方程为

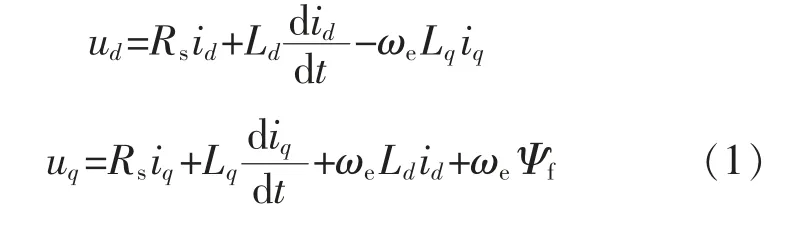
式中：ud、uq为定子电压在d、q 轴分量；Rs为定子电阻；id、iq为定子电流在d、q 轴分量；Ld、Lq为d、q 轴电感；ωe为电机电角速度；Ψf为永磁体磁链[1]。

PMSM 运动方程为

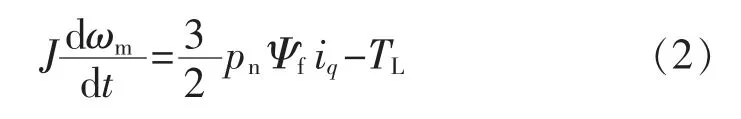
式中：J 为转动惯量；ωm为电机角速度；pn为磁极对数；TL为负载转矩。

2 滑模速度控制器设计

由式（1）和式（2）可得永磁同步电机状态方程为

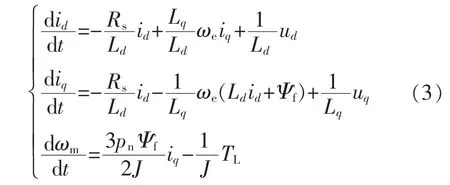
定义永磁同步电机系统状态变量为

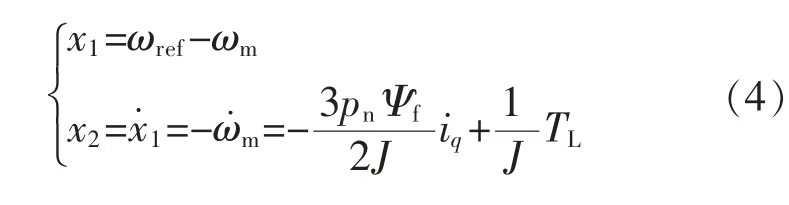
式中：ωref为电机的转速给定；ωm为实际转速。

由于积分滑模面可以平滑过渡，减小系统稳态误差，削弱抖动，且变量中无变量的二阶导数，增强控制器的稳定性。因此，定义滑模面为

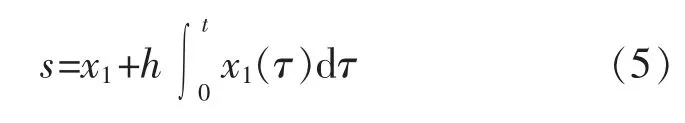
式中：h 为正系数。

则由式（5）可得：

将式（4）带入式（6）可得：

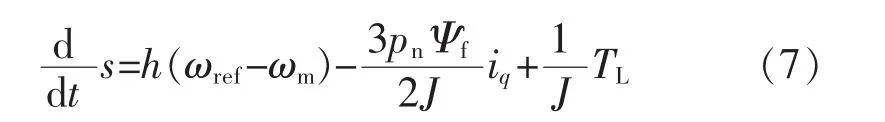
由于实际电机运行时存在参数不匹配及扰动问题，因此假定：

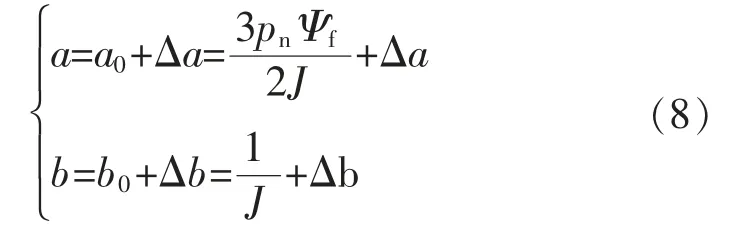
式中：a0、b0为永磁同步电机系统中电机的设定参数；Δa、Δb 为永磁同步电机实际参数值与设定值之间的差值。

同时，在式（7）中加入系统中可能存在的有限的扰动c 即可得到：

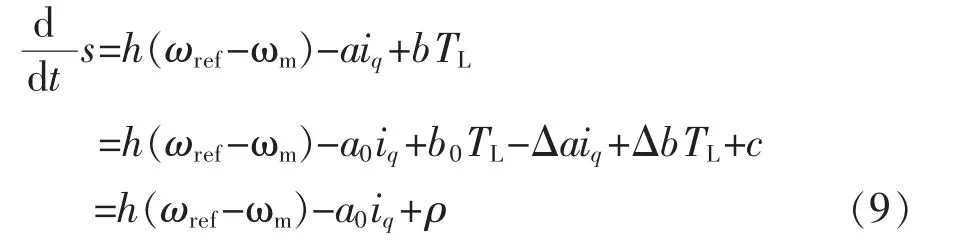
式中：ρ=b0TL-Δaiq+ΔbTL+c

假设系统的总扰动量ρ 为一个有限的缓慢变化的量，则我们设ρ 的估计值为，它们的差值为。由此，为使滑模面与扰动值渐进稳定，设计控制量u 为

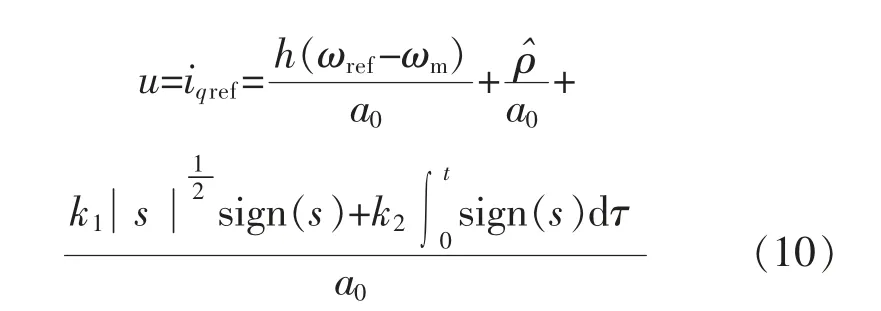
式中：k1、k2为正系数。

定义Lyapunov 函数为

则其导数为

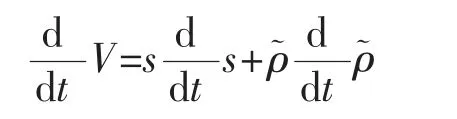
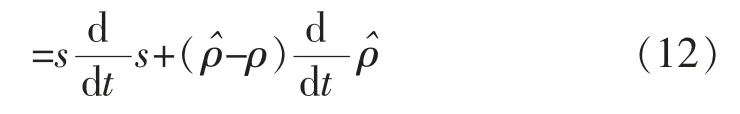
将式（9）、式（10）带入式（12）可得

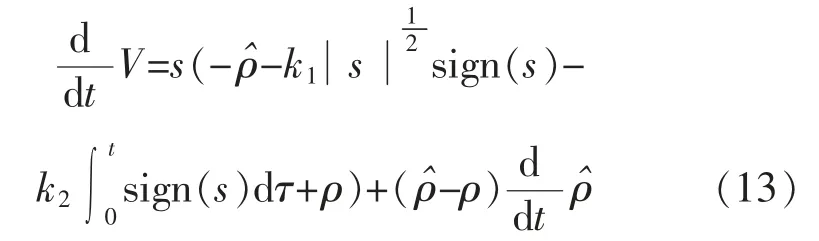
定义自适应律为

可得：

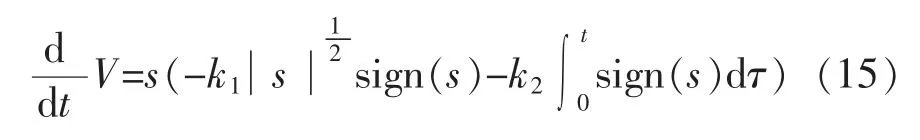
即设定合适的自适应律后整个系统的稳定性证明转化为Super-twisting 算法渐进稳定性的证明。

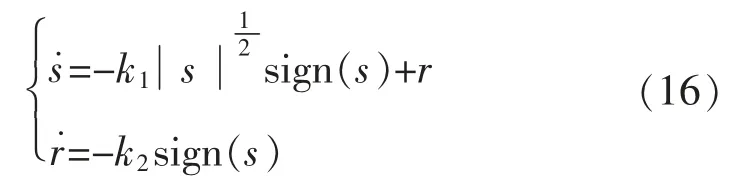
为证明二阶滑模算法的渐进稳定性，令A=矩阵Q，一定存在一个正定矩阵P 满足Lyapunov方程

选取Lyapunov 函数为

则由式（18）可得：

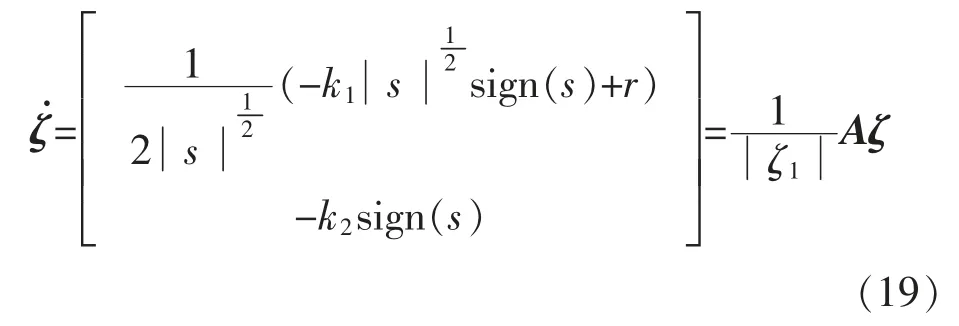
所以对V（s，r）求导可得：

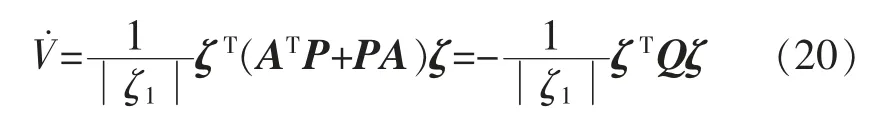
因为V 为二次正定函数，所以有：

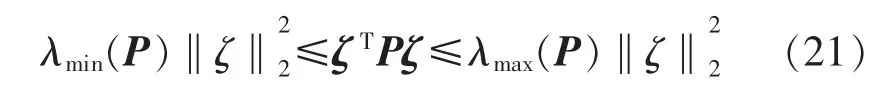
式中：λmin（P）、λmax（P）分别为P 的最小和最大特征值，，进一步可得：

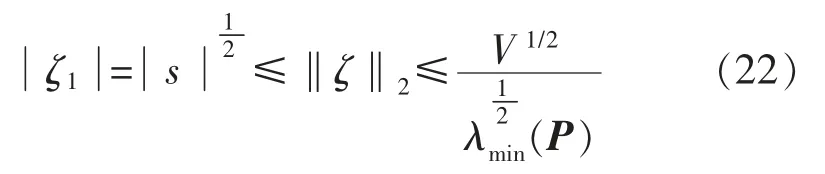
综合式（20）和式（22）可得：

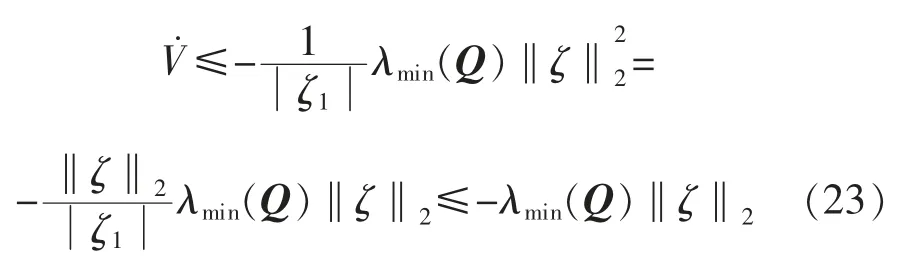
由式（20）可得：

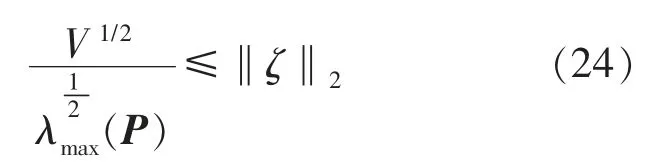
综合式（23）、式（24）可得：

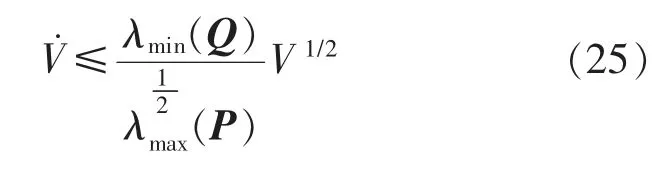
综上，基于Super-twisting 算法的自适应滑模速度控制器能在有限时间内使系统达到渐进稳定。

3 仿真验证及结果分析

为验证基于Super-twisting 算法的自适应滑模速度控制器的可行性与稳定性能，基于MATLAB/Simulink 搭建了PMSM 矢量控制系统，如图1所示。本系统采用了传统的id=0 控制对永磁同步电机进行控制。其中自适应滑模速度控制器模块由式（10）搭建而成，以电机角速度给定值与实际值的差值为输入，通过基于Super-twisting 算法的自适应滑模控制器对系统控制量iqref进行给定。仿真中永磁同步电机参数如表1所示。

为验证本文提出的自适应滑模速度控制器的控制效果，取经典指数趋近律滑模速度控制器作为对比。除速度控制器模块外，包括电流环、SVPWM、永磁同步电机等模块均完全一致。设置给定转速为800 r/min，并在0.2 s 时施加10 N/m 的负载转矩。

图1 基于Super-twisting 算法的自适应滑模控制的PMSM 调速模型Fig.1 PMSM speed regulation model of adaptive sliding mode control based on Super-twisting algorithm

表1 永磁同步电机参数Tab.1 Permanent magnet synchronous motor parameters

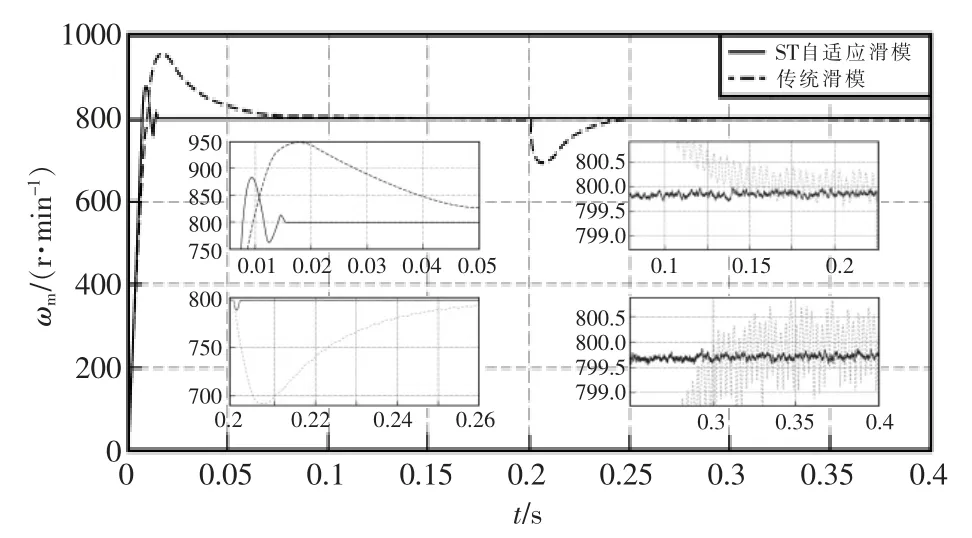
图2 给定转速800 r/min 下电机转速响应对比图Fig.2 Comparison of motor speed response at a given speed of 800 r/min

由图2 可以看出当电机从零速上升到参考转速800 r/min 时，ST 自适应滑模控制的超调量只有85 r/min 左右，相比较传统滑模控制的154 r/min减小了将近45%，且动态响应速度明显优于传统滑模控制，从0.1 s 减小到了0.017 s 左右。当0.2 s 时对电机施加10 N/m 时，可以看出ST 自适应滑模控制的转速降只有11 r/min 左右，相较于传统滑模控制的108 r/min 减小了近90%，而稳定时间相对却减少了0.0785 s。综上，ST 自适应滑模算法在降低超调、负载波动以及快速稳定上性能都明显优于传统滑模控制，提高了系统的动态性能。又由加载前后静态局部放大图可以看出加载前后传统滑模速度控制下，转速波动有略微增大趋势，而ST 自适应滑模速度控制下速度波动较小，且波动明显优于传统滑模控制，可见新型滑模速度控制静态特性也优于传统滑模控制。

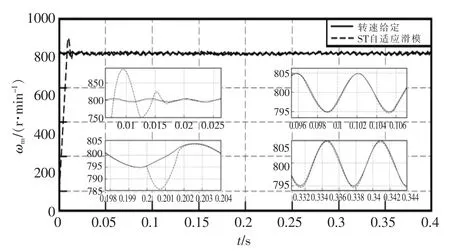
图3 给定转速800 r/min 上下5 r/min 波动电机转速响应图Fig.3 Speed response diagram of the motor with a fluctuation of 5 r/min up and down at a given speed of 800 r/min

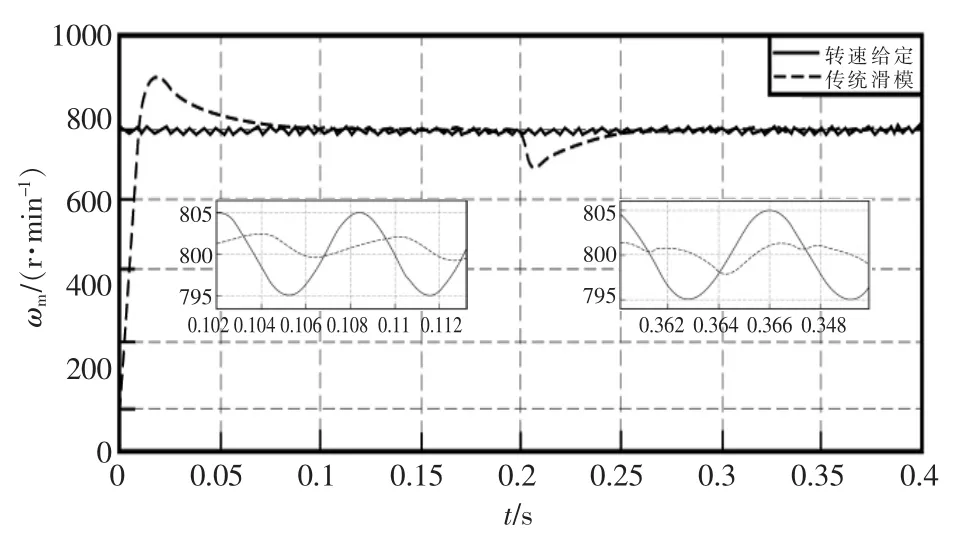
图4 给定转速800 r/min 上下5 r/min 波动电机转速响应图Fig.4 Speed response diagram of the motor with a fluctuation of 5 r/min up and down at a given speed of 800 r/min

由图3、图4 可以看出当给定800 r/min 上下5 r/min 波动时，ST 自适应滑模控制下的转速响应依旧能很好的跟随，而传统滑模控制则无法快速跟随。可见ST 自适应滑模速度控制器性能确实优于传统滑模速度控制。

4 结语

针对PMSM 交流调速系统中使用传统滑模速度控制器时，转速超调大、加载时转速下落大、到达稳态时间长以及鲁棒性差的问题，提出了一种基于Super-twisting 算法的自适应滑模速度控制器以代替传统的滑模速度控制器。基于MATLAB/Simulink 对新型滑模速度控制器进行仿真验证，结果表明相较于传统滑模控制器，新型滑模速度控制器超调小，到达稳态时间短，且鲁棒性优越。