铅芯橡胶支座对梁拱组合结构的减震效果研究*

李超，甘耀威，秦世强

武汉理工大学土木工程与建筑学院，湖北武汉430070

连续梁拱组合结构桥梁的主跨分布集中在100～200 m，能够实现较大的跨径，且承载能力以及造价方面都有优势［1］。连续梁拱组合结构桥梁能通过施加预应力在梁内以抵消桥墩承受的水平推力，在拥有良好的结构特性的同时，也能凭借优美的造型成为地标性建筑，因而在公路和铁路大跨桥梁建设中得到了广泛的应用［2］。

基于屈服机理，杜骞等［3］认为在横向地震作用下拱脚和拱顶在横向上不一定首先屈服；杨涛［4］对某连续梁拱组合桥进行了抗震分析，认为考虑边界非线性问题更能反映结构在地震时的实际反应情况；申现龙等［5］以非线性时程分析法的结果为基准，评估了Pushover法在桥梁整体及局部构件地震需求估算中的有效性及误差范围，认为系杆拱桥纵向地震需求评估与NL-THA 方法分析结果趋势相似；高明等［6］对橡胶含量不同的钢管混凝土拱桥进行了非线性动力时程分析，认为钢管橡胶混凝土拱肋能降低结构的自振频率，延长结构的自振周期。施成［7］将减隔震支座运用到大跨度连续钢桁架柔性拱桥，认为添加减隔震支座能减小地震响应并延长自振周期；何磊［8］将多种不同支座运用到钢管混凝土拱桥，认为不同支座类型对结构的减隔震效果影响较大；戴公连等［9］对兰渝线上某连续梁拱组合桥设置速度锁定装置并进行了减震效果分析，认为速度锁定装置能显著减小固定墩的墩顶位移和墩底内力；Liu Hao等［10］分析了纵向地震动作用下铁路桥面拱桥的地震响应，认为铁路拱桥抗震设计中应考虑轨道约束。可以看出，已有众多学者对拱桥的动力特性及减震进行了研究；也有学者通过改变拱肋材料组成成分来降低结构地震响应。然而连续梁拱组合结构有别于常规拱桥，尤其是大跨径连续梁拱组合，关于其动力特性的研究也还不够，仍需系统分析不同因素对其动力特性的影响［11-13］。对于连续梁拱组合结构的减震研究则涉及更少，没有提出完善的结构减震设计方法和建议。

太原市南中环桥主拱肋外倾呈蝶形拱形式，是一座大跨度连续梁拱组合结构桥梁。本文以南中环桥为研究对象，通过结构自振特性确定其模态参数，并对铅芯橡胶减隔震支座的非线性分析模型与等效线性模型、力学特性参数计算进行了研究；在此基础上，对结构主要控制截面进行了减震设计。

1 工程概况

南中环桥跨径组合为60 m+180 m+60 m，桥梁标准宽度为52.5 m。主桥为拱梁组合结构，采用钢叠合梁组合式系杆拱体系，主桥中跨跨中92 m；梁段采用钢叠合梁，梁高3.0 m，主桥边跨60 m，主桥中跨44 m；梁段采用混凝土箱梁，梁高3.0～6.5 m。原始设计采用适用于-25～60 ℃的固定支座、多向活动支座和单向活动支座3 种球型钢支座，将结构内力与位移通过构件本身平面与球面摩擦副的承载与滑动传递到下部结构。支座主要由支座板、球面非金属滑板、球面不锈钢板、平面非金属滑板等组成，具有足够的承载力和压缩变形能力，且支座滑动摩擦系数不大于0.03，球面不锈钢板与非金属滑板间设计摩擦系数为0.03。结构抗震设防烈度8 度，基本加速度值为0.20 g，重要性修正系数1.7；桥跨纵向布置如图1 所示。该桥结构复杂，体系为公路桥梁连续梁拱代表之作，故对其进行减震设计研究具有重要意义。

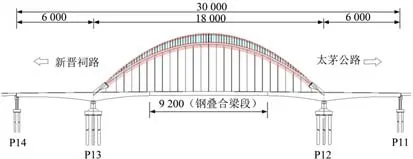
图1 南中环桥全桥布置图Fig.1 Nanzhonghuan Bridge full bridge layout

2 动力特性分析

结构的自振特性是结构动力行为研究的基础。采用通用有限元分析软件MIDAS/CIVIL 对结构自振特性进行仿真分析，全桥共离散为6 174 个节点，8 364 个单元，其中94 个桁架单元，8 270 个梁单元，该桥有限元模型如图2所示。在静力分析中，采用边界条件＞弹性连接＞一般（类型）来模拟球型钢支座，此时需要对三个平动方向和三个转动方向的刚度数值各自进行输入，各支座刚度数值如表1 所示，支座的原始设计形式如图3所示。

图2 南中环桥三维有限元模型Fig.2 Three-dimensional finite element model of Nanzhonghuan Bridge

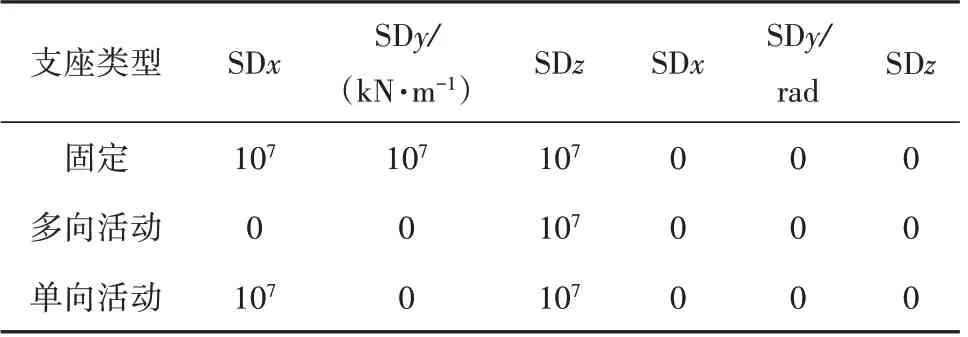
表1 支座原始设计刚度值Table 1 Original design stiffness value of bearing

图3 原始设计支座布置形式Fig.3 Original design support arrangement

子空间迭代法的最大优点是能显著减少特征方程阶数，高效求解特征向量和特征解。采用子空间迭代法对南中环桥进行自振分析，选择性的选取结构前20 阶具有代表性的自振频率、振型特征，如表2所示。

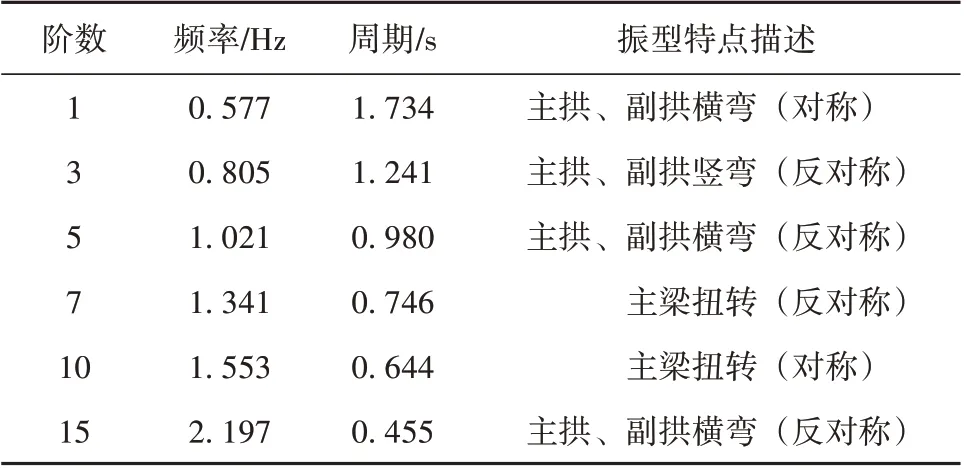
表2 结构自振频率及振型特征表Table 2 Structure self-vibration frequency and vibration mode characteristics

该桥拱肋面外横弯最早出现在第一阶振型，自振频率为0.577；拱肋竖弯最早出现在第三阶振型，自振频率为0.805；主梁扭转最早出现在第七阶振型，自振频率为1.341。与面内刚度相比，拱肋面外刚度较小，结构整体横向稳定性不足，为了提高其抗震性能则必须考虑结构整体的横向稳定性。

3 连续梁拱组合结构减震设计

纵向位移过大则可能发生支撑结构损坏、落梁现象；而过大的横向位移则可能导致结构失稳、主梁倾覆［14］。科学合理的减隔震装置，对减小控制截面响应值显得至关重要［15］。根据该桥的实际情况和体系特征，采用铅芯橡胶减隔震支座进行减震设计。

3.1 荷载加载形式

根据规范规定，该桥场地为基岩，场地系数R取0.65。在E1和E2地震荷载作用下，结构水平设计加速度反应谱曲线如图4所示。

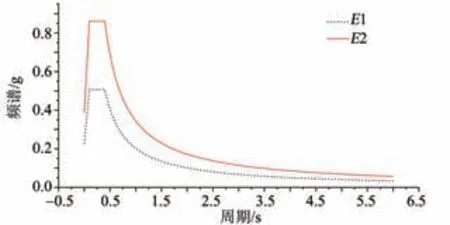
图4 水平向加速度反应谱曲线Fig.4 Horizontal acceleration response spectrum curve

考虑到场地尚未有实测地震波记录，采用SIMQKE_GR 选波软件对反应谱波进行拟合［16］。基本思路是以迭代法为基础求解功率谱密度函数，接着求解傅立叶幅值谱，最后经傅立叶逆变换得到稳定加速度时程曲线，根据时间包络函数则可以得到一般加速度时程曲线。选择拟合程度较好的3条人工地震波作为动态时程曲线输入，地震波作用下的最大响应值作为分析结果。仅E2 地震动作用下的结构加速度时程曲线如图5所示。

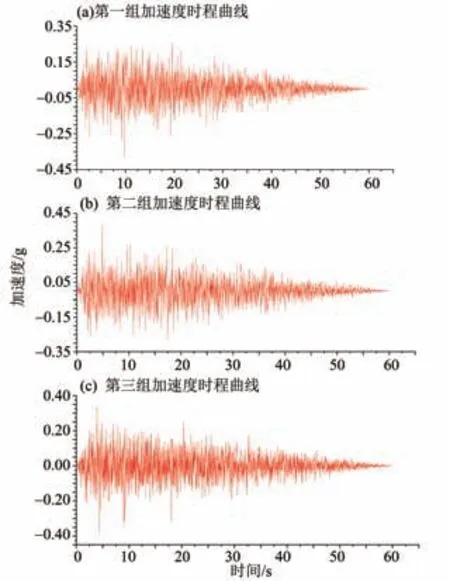
图5 人工合成三条加速度时程曲线图Fig.5 Synthetic three acceleration time history curves

选择CQC 振型组合法对结构进行振型叠加计算，并取前90 阶振型。结果显示：在X、Y 和Z 三个平动方向上，其振型的质量累计贡献率分别达99.88%、99.98%和95.27%。在X、Y 方向上，结构具有对称性，因此进行地震响应结果分析时，仅对结构单侧各个控制截面进行响应分析，各个控制截面的位置如图6所示。

3.2 支座布置形式

隔震效果的优劣受支座布置形式的影响十分明显。为了使设置隔震支座后结构地震响应更加合理分配，降低结构最不利地震响应，主梁中心线仍采用原始设计支座（球型钢支座），两侧采用铅芯橡胶隔震支座替换原始设计支座，其结构支座设置和布置形式如图7所示。

3.3 非线性分析模型与等效线性模型

铅芯橡胶支座力学模型分为两类：非线性分析模型和等效线性模型［17］。前者主要用于非线性动（静）力分析，主要设计参数包括硬化比、弹性刚度以及屈服强度；后者主要用于线弹性动力特性分析，主要设计参数包括等效阻尼比、等效刚度。铅芯橡胶支座滞回曲线及双线性力学模型如图8所示。

对结构进行非线性动、静力分析主要设计参数计算，即

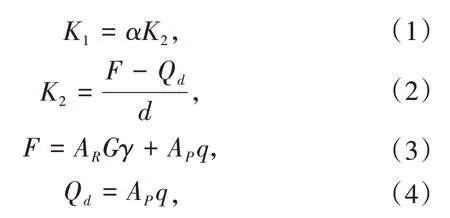
式中K1表示铅芯橡胶支座的弹性刚度；K2表示铅芯橡胶支座屈服后的刚度；F 表示铅芯橡胶支座承受的最大剪力；Qd表示铅芯橡胶支座屈服荷载；d表示有效设计位移；G表示橡胶的剪切模量；AR表示橡胶承压面积；AP表示铅芯截面面积；γ 表示铅芯橡胶支座有效剪应变；q 表示铅芯受力变形产生的剪切应力为［18］

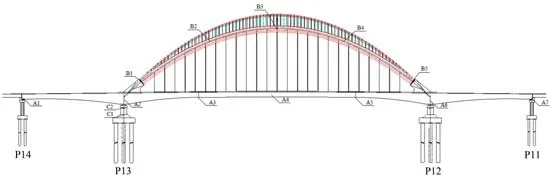
图6 南中环桥地震响应分析控制截面示意图Fig.6 Schematic diagram of control section of seismic response analysis of Nanzhonghuan Bridge

图7 隔震支座布置形式Fig.7 Isolation bearing arrangement

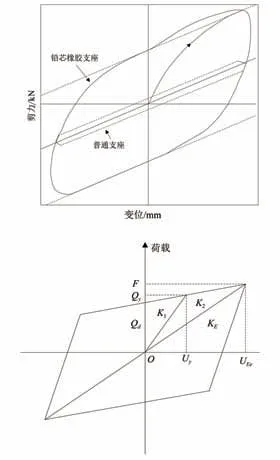
图8 铅芯橡胶支座滞回曲线及双线性模型Fig.8 Hysteresis curve and bilinear model of lead rubber bearing

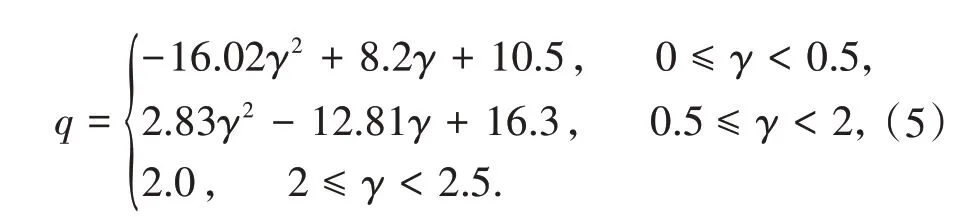
等效线性模型普遍用于弹性反应谱分析，基本原理是通过线性模型近似分析非线性隔震支座。支座关键参数等效刚度和等效阻尼比为

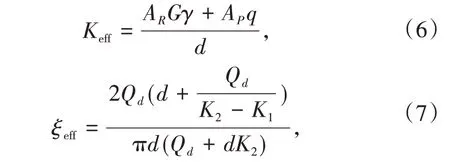
式中各项参数的含义与非线性分析模型中的一致。支座中铅芯的直径和数量直接决定等效刚度和等效阻尼的值，从而影响结构的减震效果。

3.4 力学特性参数计算

铅芯橡胶支座的力学特征参数如铅芯截面面积、硬化比和隔震支座尺寸决定了支座的减震效果［17］。其中，铅芯截面面积影响支座减震耗能能力。当铅芯高度与铅芯直径比在1.5～5.0的范围内时，支座减震耗能能力越强则表示铅芯截面面积越大。硬化比表示为支座屈服后刚度与屈服前刚度的商，铅芯截面面积、铅芯有效变形高度、橡胶种类和支座尺寸均影响硬化比值。屈服前，铅芯截面面积增大，硬化比值也随之增大；屈服后，橡胶硬度和支座尺寸越大，则支座屈服后刚度越大。隔震支座尺寸直接影响其屈服后刚度，支座安装的空间和位置也会影响其减震效果。

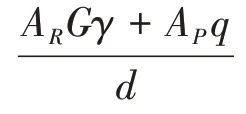
3.5 铅芯橡胶支座减震效果分析

根据规范规定：A类桥梁结构抗震计算时，竖向地震动所引起的结构地震响应必须重视。对结构进行地震响应分析时考虑组合地震动的影响，即“纵向+竖向地震动”（工况一）和“横向+竖向地震动”（工况二）的空间效应组合。因篇幅有限，仅列举E2 地震动作用下主拱肋控制截面的地震响应结果。将结构以时程分析法得出的响应值与不同铅芯截面面积、硬化比和隔震支座尺寸的响应值作对比，分析结构在隔震后的地震响应规律。引入隔震率=（时程分析响应最大值-设置隔震支座后的响应最大值）/时程分析响应最大值，隔震前的最大响应出现在B2、B3和B5截面处。结构减震分析时，墩底截面处的地震动响应也是主要分析对象。

3.5.1 铅芯截面面积 初步选取仅直径不同，其他力学特性参数相同的铅芯橡胶支座如表3 所示。“工况二”下B3 位移隔震率，如图9 所示。组合地震动作用下B5 内力隔震率，如图10 所示。在E2地震动作用下，隔震模型各控制截面的地震响应如表4所示。

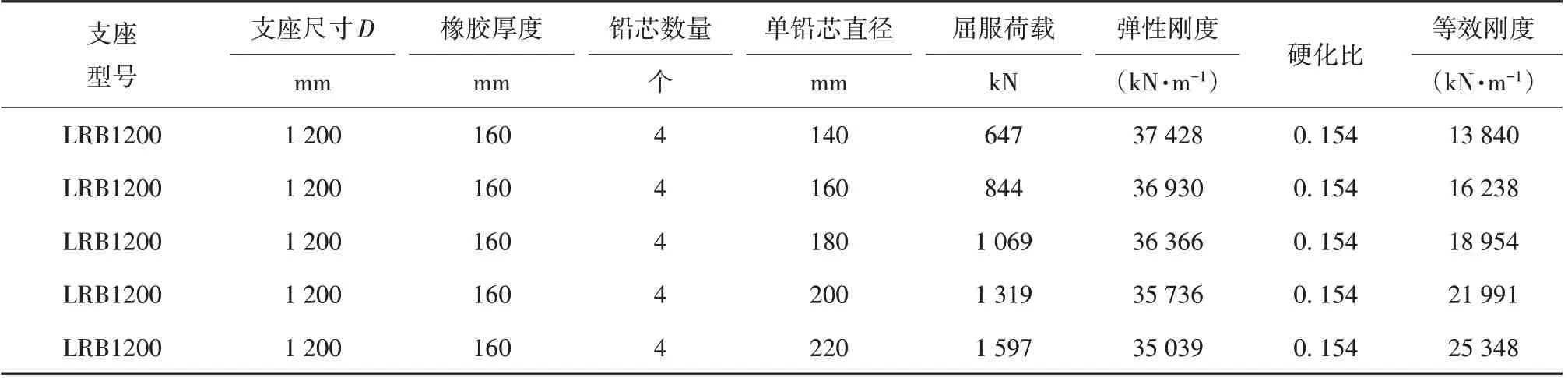
表3 不同铅芯直径下铅芯橡胶支座力学特性参数Table 3 Mechanical properties of lead rubber bearing under different lead core diameters

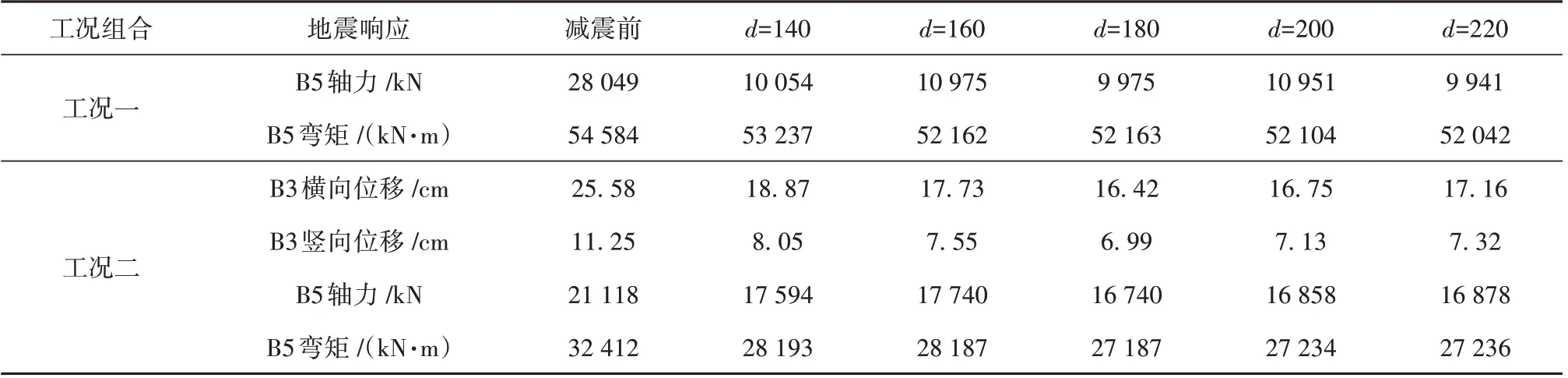
表4 不同铅芯直径下结构减震效果分析Table 4 Analysis of structural damping effect under different lead core diameters

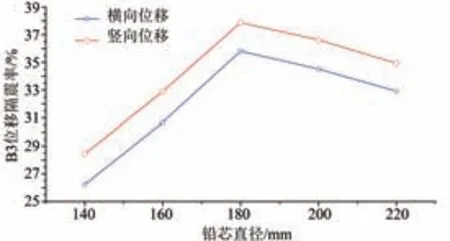
图9 “工况二”下B3位移隔震率Fig.9 B3 displacement isolation rate under"condition 2"

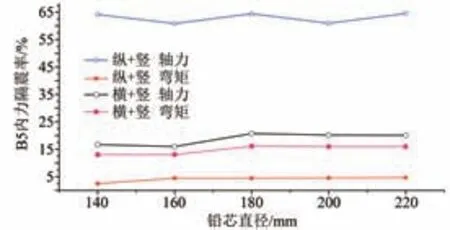
图10 组合地震动作用下B5内力隔震率Fig.10 B5 internal force isolation rate under combined ground motion

可以看出：设置减隔震支座后控制截面的时程响应得到了较大幅度的减小；当其他力学特性参数相同仅直径不同时，“工况二”下铅芯直径为180 mm 时减震效果最佳，B3 截面处最大横、竖向位移减震率分别达35.8%和37.9%，且竖向减震效果优于横向隔震效果；“工况一”作用下B5截面处最大弯矩减震率仅4.7%。

3.5.2 铅芯硬化比 当铅芯直径D=180 mm，硬化比分别为0.1、0.127、0.154、0.181 和0.208时，其他力学特性参数不变的铅芯橡胶支座隔震模型各控制截面的地震响应如表5 所示。“工况一”下B2 位移隔震率，如图11 所示。组合地震动作用下C2内力隔震率，如图12所示。

可以看出，当其他力学特性参数相同仅硬化比不同时，“工况一”作用下硬化比为0.154 时减震效果最佳，B2 截面处纵、竖向最大位移减震率分别达48.1%和42.2%，且纵向减震效果优于竖向隔震效果；组合地震动作用下C2 截面处最大弯矩减震率为34.2%。

3.5.3 隔震支座尺寸 在铅芯直径D=180 mm、硬化比α=0.154，隔震支座尺寸为800 ～1 600 mm，其他力学特性参数相同的铅芯橡胶支座隔震模型各控制截面的地震响应如表6 所示。“工况一”下B2位移隔震率，如图13 所示。“工况二”下B3 位移隔震率，如图14 所示。组合地震动作用下B5 内力隔震率，如图15所示。

可以看出，当其他力学特性参数相同仅隔震支座尺寸不同时，“工况一”作用下隔震支座尺寸为1 200 mm 时减震效果最佳，B2 截面处纵、竖向最大位移减震率分别达48.1%和42.2%，且纵向减震效果优于竖向隔震效果；“工况二”作用下隔震支座尺寸为1 400 mm 时B3 截面的最大竖向位移减震率达48.1%，隔震支座尺寸为1 000 mm 时B3截面的最大横向位移减震率达37.1%，且竖向减震效果优于横向隔震效果；组合地震动作用下B5截面处最大轴力减震率为64.4%，而在“工况一”不同支座尺寸下最大弯矩减震率几乎保持不变，仅为5.0%。

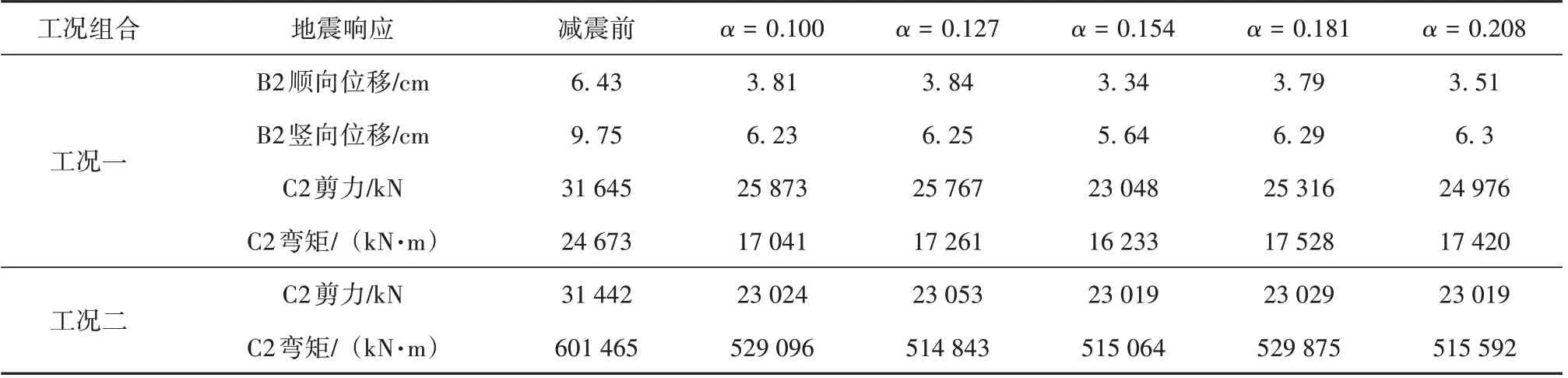
表5 不同硬化比下结构减震效果分析Table 5 Analysis of shock absorption effect of structures under different hardening ratios

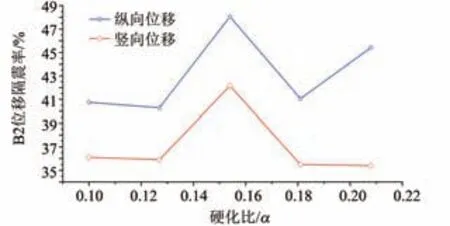
图11 “工况一”下B2位移隔震率Fig.11 B2 displacement isolation rate under"condition 1"

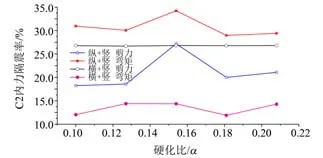
图12 组合地震动作用下C2内力隔震率Fig.12 C2 internal force isolation rate under combined ground motion

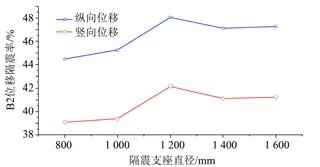
图13 “工况一”下B2位移隔震率Fig.13 B2 displacement isolation rate under"condition 1"

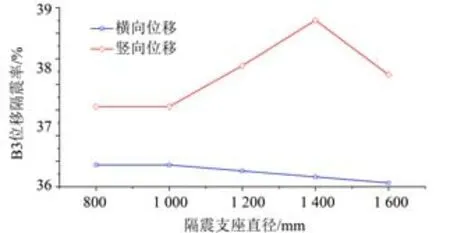
图14 “工况二”下B3位移隔震率Fig.14 B3 displacement isolation rate under"condition 2"

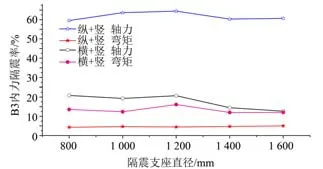
图15 组合地震动作用下B5内力隔震率Fig.15 B5 internal force isolation rate under combined ground motion

4 结 论

建立南中环桥Midas 有限元模型，按照要求设置铅芯橡胶减隔震支座后，对结构进行地震响应时程分析，得出的主要结论如下：

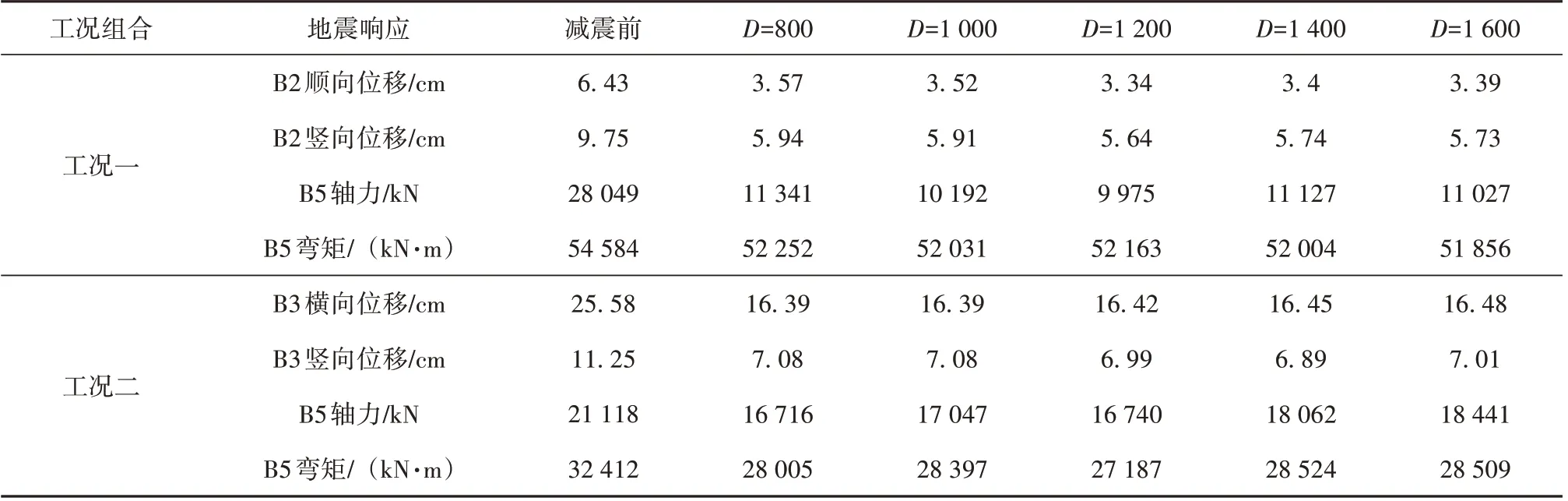
表6 不同隔震支座尺寸下结构减震效果分析Table 6 Analysis of structural damping effect under different isolation bearing sizes

1）设置隔震支座后，主拱控制截面的位移响应值均有不同程度的下降。在两种组合地震动作用下，与纵向和竖向位移隔震效果相比，横桥向隔震率较低，主要受到主拱肋面外刚度的影响；

2）结构原始设计支座的存在，会限制结构位移最值，显著降低位移响应；因仅仅设置了部分隔震支座，故在拱脚B5 截面处，与其他控制截面相比结构内力响应值降幅较小；

3） 该桥进行减震设计时，取铅芯直径D=180 mm、硬化比α=0.154、支座直径为1 200 mm，其他力学特性参数不变时，结构减震效果最佳。